浅层地下爆炸层析成像信息优化获取技术*

白苗苗,王黎明,高 蕊,范学军,王 可

(中北大学信息与通信工程学院,太原 030051)



浅层地下爆炸层析成像信息优化获取技术*

白苗苗,王黎明*,高 蕊,范学军,王 可

(中北大学信息与通信工程学院,太原 030051)

基于地震层析成像理论提出了地下爆炸冲击波超压时空场重建技术。从模型离散化和传感器布局两方面进行成像信息优化,提高地下爆炸场层析成像信息的有效性。模型离散化方面,根据冲击波的的衰减规律,提出了不规则网格划分方法;传感器布局方面,根据数学上欠定问题理论与地震波传输规律,提出了指导传感器布局的指标及优化算法,实现传感器合理布局。仿真表明,层析成像信息优化获取技术可以最大限度地提高数据利用率,使得反演过程更稳定,反演误差更小。

传感器;优化布局;地震层析成像;超压场重建;地下爆炸

武器在地下爆炸,他们的破坏作用主要是爆炸产生的冲击波和应力波来摧毁目标。准确地评价这些高效能武器系统的杀伤力是武器系统在研制和靶场验收等过程中急需解决的问题,因此需要准确可靠的测试手段为武器系统的研究提供依据。

目前爆炸测试的主要方法是在不同爆心距布放传感器获取爆炸信息,或者进行数值模拟[1-2],这种局部的方法只能测得空间有限位置的爆炸参数值,对于不规则弹药造成的不均匀毁伤,局部点测试方法不能全面获取爆炸信息,从而不能准确评估爆炸威力。本文基于地震层析成像的理论,提出地下爆炸场层析成像,即在有效测试区域内,以有限测试点代替无限测试点,实现地下爆炸的超压场时空分布,为武器系统毁伤效能评估提供依据[3]。

地下爆炸场层析成像归结为单一激励源稀疏射线层析成像问题,其射线呈稀疏分布,层析成像方程是欠定的、病态的。此类层析成像问题,信息的有效利用是非常关键的。本文主要从模型离散化和传感器优化布局[4]两方面研究地下爆炸层析成像信息优化技术,最大限度地提高信息的有效性,降低数据的冗余性,从数学根源上改善层析成像问题。

1 层析成像信息优化获取依据及评价方法

1.1 理论依据

本文采用层析成像的方法重建地下爆炸超压场,即在中心炸点周围布放M个传感器,爆炸后冲击波从中心炸点到传感器形成M条传播路径射线;根据冲击波的传输规律,将所要重建的区域划分为N个不规则的离散网格单元,通过对各个传感器阵元采集获得的冲击波信号进行分析及特征提取,得到冲击波到达时间(走时),采用走时层析[5-6]方法重建测试区域内各网格单元冲击波速度。最后根据速度与冲击波峰值超压的关系,将每个网格的速度值转换成超压值,重建出整个二维面上的平面冲击波超压值。

地下爆炸场层析成像归结为求解矩阵方程:

DS=T

(1)

式中:T=(t1,t2…tM)′为各条射线走时,是一个M维列向量,为试验测试值;S=(s1,s2…sN)′为待求离散单元慢度值,是一个N维的未知的列向量;D为M×N阶稀疏矩阵。

爆炸场层析成像本就是一个病态方程组的求解问题,由式(1)可知,影响方程解的唯一因素是系数矩阵D,因此要改善病态不适定反演问题的稳定性就要改善矩阵D的结构。矩阵D的元素dij代表第i条射线在第j个网格单元内的长度,故矩阵D的结构取决于反演区域的模型离散和测试射线也就是传感器的布局。因此,我们需要从模型离散化和测试传感器布局两方面进行优化设计。

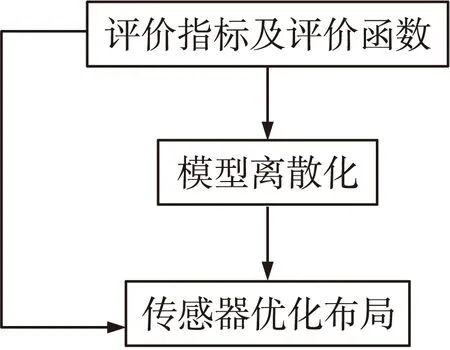
图1 地下爆炸场层析成像信息优化获取技术结构图

1.2 层析成像信息优化获取方案及评价方法

1.2.1 评价指标

从矩阵的观点求解方程(1),也就是求系数矩阵D的逆矩阵问题,但是对于地下爆炸成像问题,系数矩阵D一般是奇异矩阵,不存在普通意义下的逆矩阵,因此需要采用广义逆理论进行求解。通过对矩阵D进行广义逆分解发现,矩阵D的奇异值和秩在求逆中担任重要因素,因此可以将矩阵D的奇异值和秩作为评价反演问题稳定性的主要指标,故定义评价指标为:

(2)

式中:λ1为DTD的最大特征值;λi为DTD的所有特征值,P为矩阵D的秩。E由两部分组成,第1部分反映了D中奇异值的相对分布情况,第2部分反映了D中零空间的相对大小情况。E越大,矩阵D的数学性质越好,反演结果也越稳定可靠。

条件数是评价方程组解质量的又一个重要指标,条件数越大,方程组的病态程度越大。故定义评价准则,

E2=cond(D)

(3)

射线密度小和正交性差的区域,反演误差大;反之,则结果比较可靠。因此可以将射线平均密度和平均正交性作为布局准则:

(4)

式中:ρj和Oj分别表示第j个网格内射线密度和射线正交性,k1和k2的取值根据具体模型的数值ρj和Oj大小决定。在进行层析成像信息优化获取时,尽可能增大射线密度和射线正交性,即E3越大越好[7-8]。

1.2.2 评价方法

由以上分析可知,由矩阵特征值和秩组成的评价函数E1、矩阵条件数E2。及射线覆盖程度均可作为判断矩阵D及方程组稳定性的指标,E1数值越大,反演结果越稳定,E2。越小,方程组越接近良性,同时,在进行射线布设时,尽可能增大E3。本文将E1、E2、E3进行加权,形成一个综合评价函数,即:

E=ω1E1+ω2/E2+ω3E3

(5)

式中:ω1、ω2、ω3的取值,根据E1、E2和E3的数量级范围进行选择,E越大越好。

由于影响病态欠定方程组的解的因素比较多,从观测系统优化布局方面而言,可以将评价函数E作为评判方程组稳定性的指标之一,在试验之前指导观测系统优化布局。本文采用评价函数E对模型离散化方式和射线分布方式进行评价,从而优化试验设计。在具体实施时,首先根据模型特点划分网格,其次,根据评价函数E对发射器和接收器进行优化布局。具体步骤如下:

①根据模型特点划分网格,利用评价函数对网格进行评价,得到最佳网格模型;

②根据试验所用发射器和接收器数目,随机给出一种布局方式,计算矩阵D,并逐一判断矩阵D的列向量是否为零向量;同时,计算矩阵D的秩;

③如果矩阵D的所有列向量都不为零向量,并且矩阵D是满秩的,则将该组布局方式记录作为优化布局的初始模型;否则,返回②;

④当初始模型达到设定数量时,将E作为目标函数,采用优化算法,进行优化布局。

2 模型离散化和传感器优化布局

2.1 模型离散化原理

模型离散化即是将测试区域离散化为若干网格单元,每个网格单元内有均匀的速度分布,网格划分方式影响矩阵D的结构。网格划分越密,层析成像的分辨率就越高,但方程的未知数就越多,解得不确定性也就越高。网格划分应结合爆炸冲击波传输规律、测试区域大小、先验信息、试验所用传感器数目合理划分。

地下爆炸时,爆炸波在距离爆炸点不同区段上出现冲击波、应力波和弹性波,如图2所示。其中冲击波是一种强压缩波,波前、波后介质的状态参数急剧变化。实质上冲击波是一种特殊的压缩波,一般压缩波压力是连续升高,而冲击波压力是急剧跃升。当发生剧烈爆炸后,冲击波的阵面也和爆轰波阵面一样,表示截止状态特征的压力、质点运动速度、密度和其他参数发生突跃。波阵面之前介质的参数和未激发之前一样,而波阵面之后,它们发生不连续变化。冲击波以超声速度传播,冲击波的波速、压力和能量随着距离很快地衰减[9]。

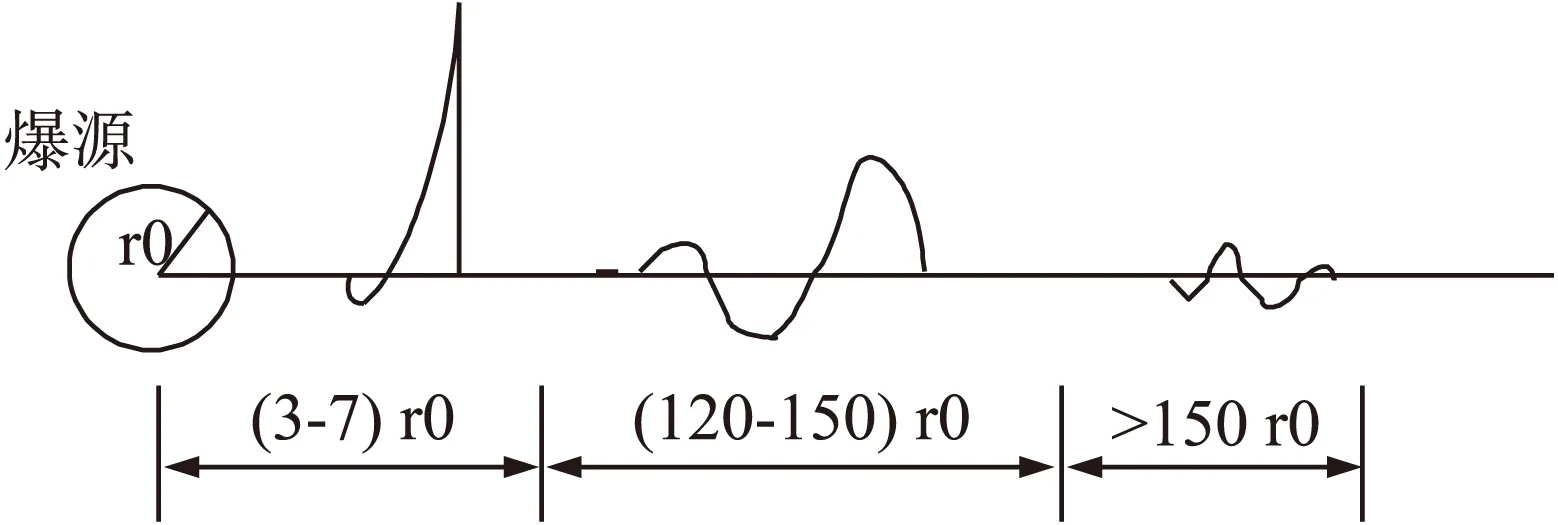
图2 各阶段上地震爆炸波形态

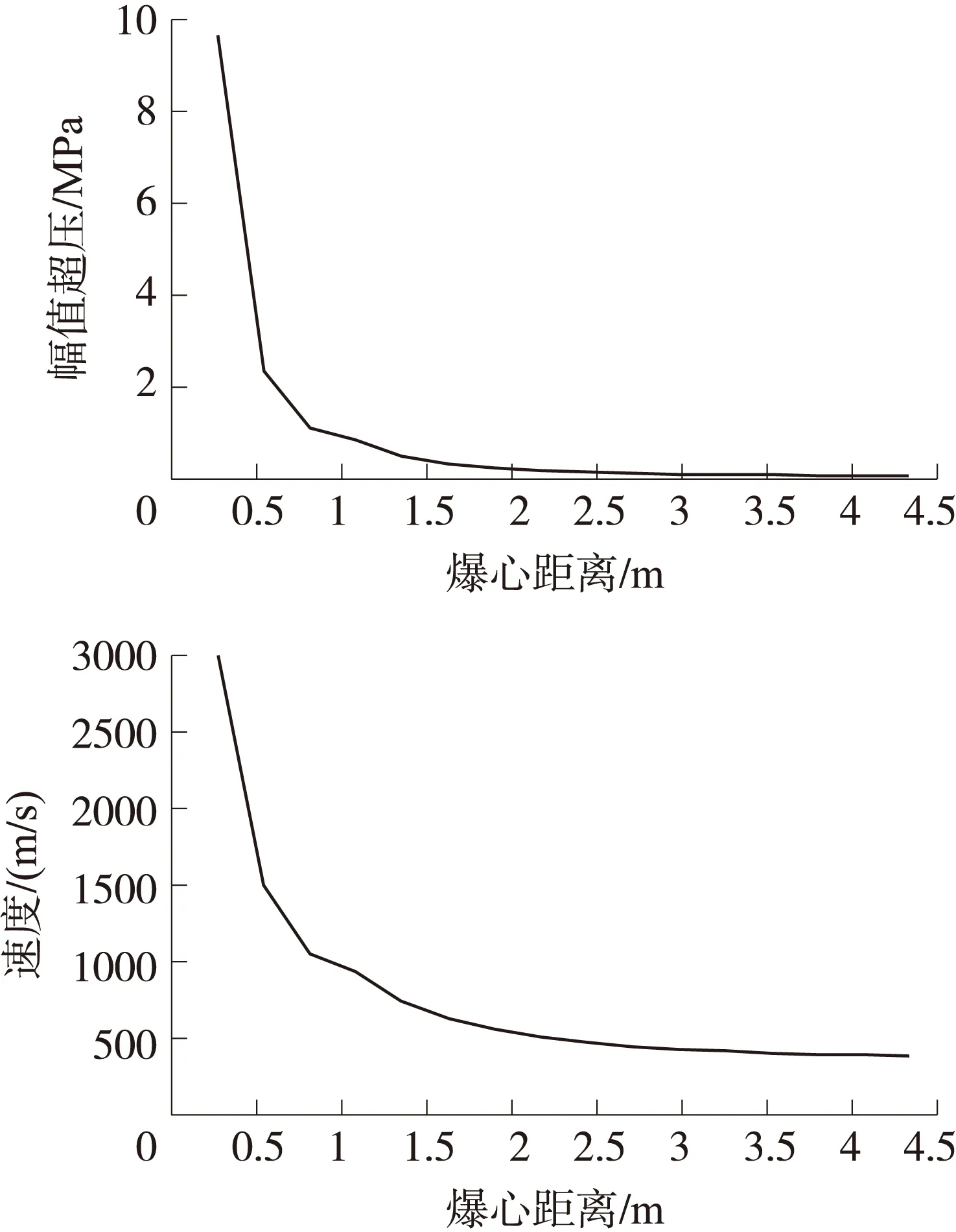
图3 冲击波峰值超压、速度随距离的变化

冲击波峰值超压随距离衰减波形如图3所示,虽然各经验公式计算结果有差异,但可以看出,在近场区,超压衰减较快,随比例距离的增大峰值超压趋于平缓。若采用均匀矩形网格划分方法,往往导致震源处超压和速度变化较快的区域出现较大的误差,故对冲击波峰值超压、速度进行重建时,不宜采用单一网格尺度,而应根据冲击波超压、速度衰减规律,结合自适应网格方法建立多尺度网格。

冲击波峰值超压与距离的关系可以用下式表示:

(6)

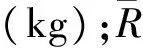
在实际应用中由于实际资料的限制得到的射线条数是有限的,要想获得相对高的成像质量网格不能划分太细,否则有些网格内的射线覆盖次数会过低甚至为零;同时,若网格划分太粗则不能保证正演时射线追踪的计算精度,同时,也使得近场区反演误差增大。

本文在分析冲击波超压衰减特点的基础上,借鉴自适应网格划分原理,提出了不规则网格划分方法,即根据爆心距离划分区域并采用不同尺度的网格,在超压衰减快的近场区,采用细网格划分方法,网格尺寸较小且网格分布稠密;在远场区采用粗网格划分方法,网格尺寸大且分布稀疏。为避免矩阵D的某些行向量线性相关,在对称区域也采用不同的网格尺度,同时,网格划分应根据试验所用传感器数目,兼顾层析成像的分辨率和精度要求。

2.2 仿真实验

以地下爆炸冲击波速度为模型进行仿真。测试区域为32 m×32 m的正方形区域,假设所使用的药包形状规则均匀且爆炸具有对称性,只对正方形爆炸区域的90°方向区域内爆炸性能进行测试,爆炸点居于测试区域原点处,传感器分布在测试区域边界。

采用两种离散模型方案对测试区域进行网格划分。第1种采用均匀矩形网格划分方法,网格数是49个,如图4所示。第2种采用本文所提出的不规则网格划分方法,如图5所示,根据冲击波速度随距离大致呈指数衰减规律,在距离爆心较近的区域,速度衰减幅度大,网格尺寸较小且网格分布稠密,故划分为近场(0～4 m)、次近场(4 m～6 m)、中场(6 m～10 m)、远场(10 m～16 m),同时避免矩阵D的某些行向量线性相关,将测试区域划分为7个区域,网格数是58,各个区域网格大小不同。

仿真结果分析如下:

①为了使得各网格均有射线穿过,均匀矩形网格所需传感器数目最少为9,而不规则网格所需传感器数目最少为5个,如图4、图5所示。

②相同射线分布情况下,均匀矩形网格对射线分布要求较高,更容易出现没有射线穿过的网格且多数情况矩阵D不满秩,如图6所示,13个传感器同样的分布,均匀矩形网格不满秩,而不规则网格满秩。

③相同射线分布情况下,不规则网格各项指标均优于均匀矩形网格。随机选取13个传感器在5种不同布站方式下,比较均匀矩形网格和不规则网格所得到的矩阵的秩、评价函数E1、条件数、射线正交性和密度,仿真数据如表1所示。由表可以看出,不规则网格更容易满秩且其条件数远远小于均匀矩形网格,同时,不规则网格射线正交性和射线密度也均大于均匀矩形网格。

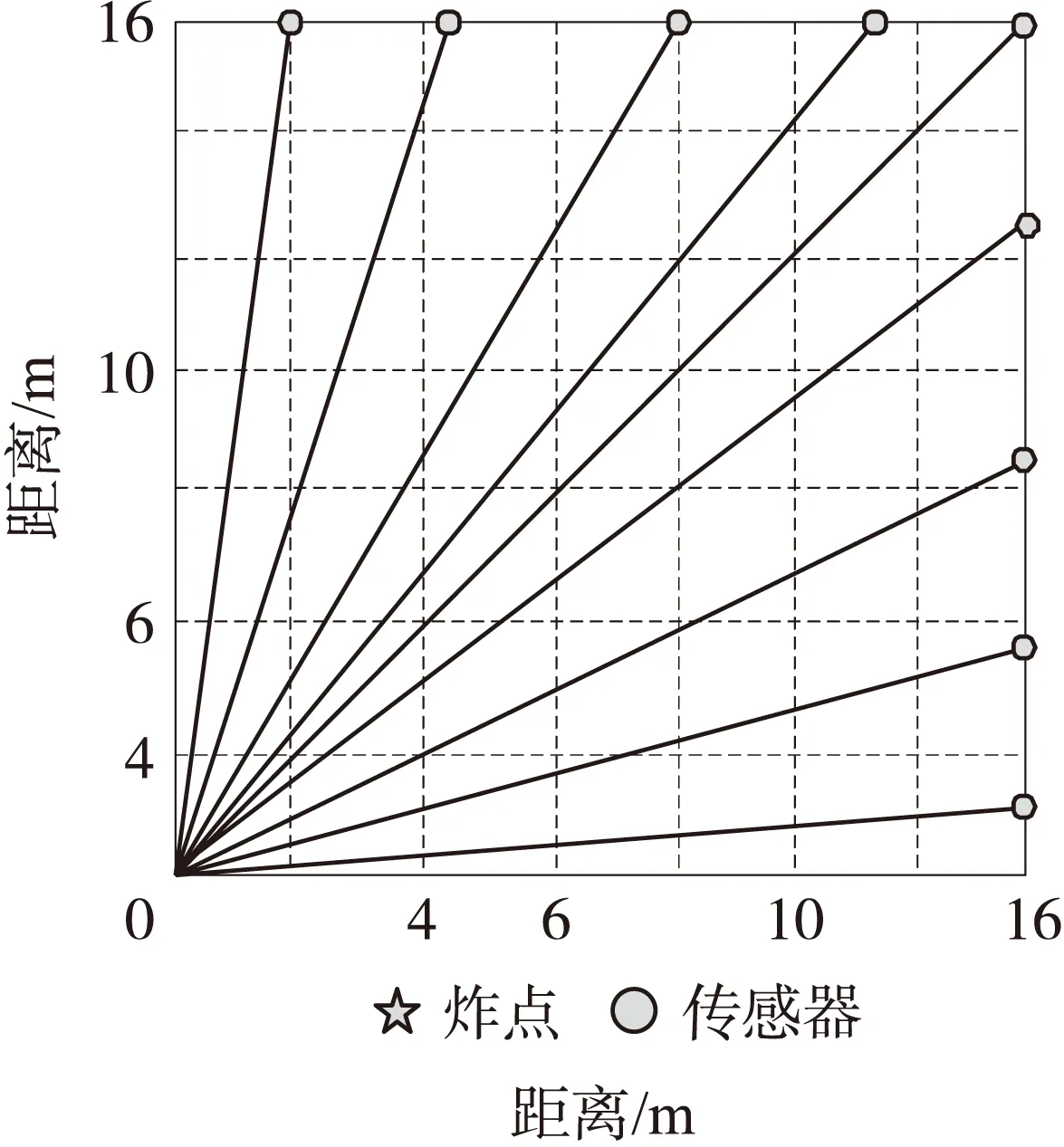
图4 均匀离散化模型

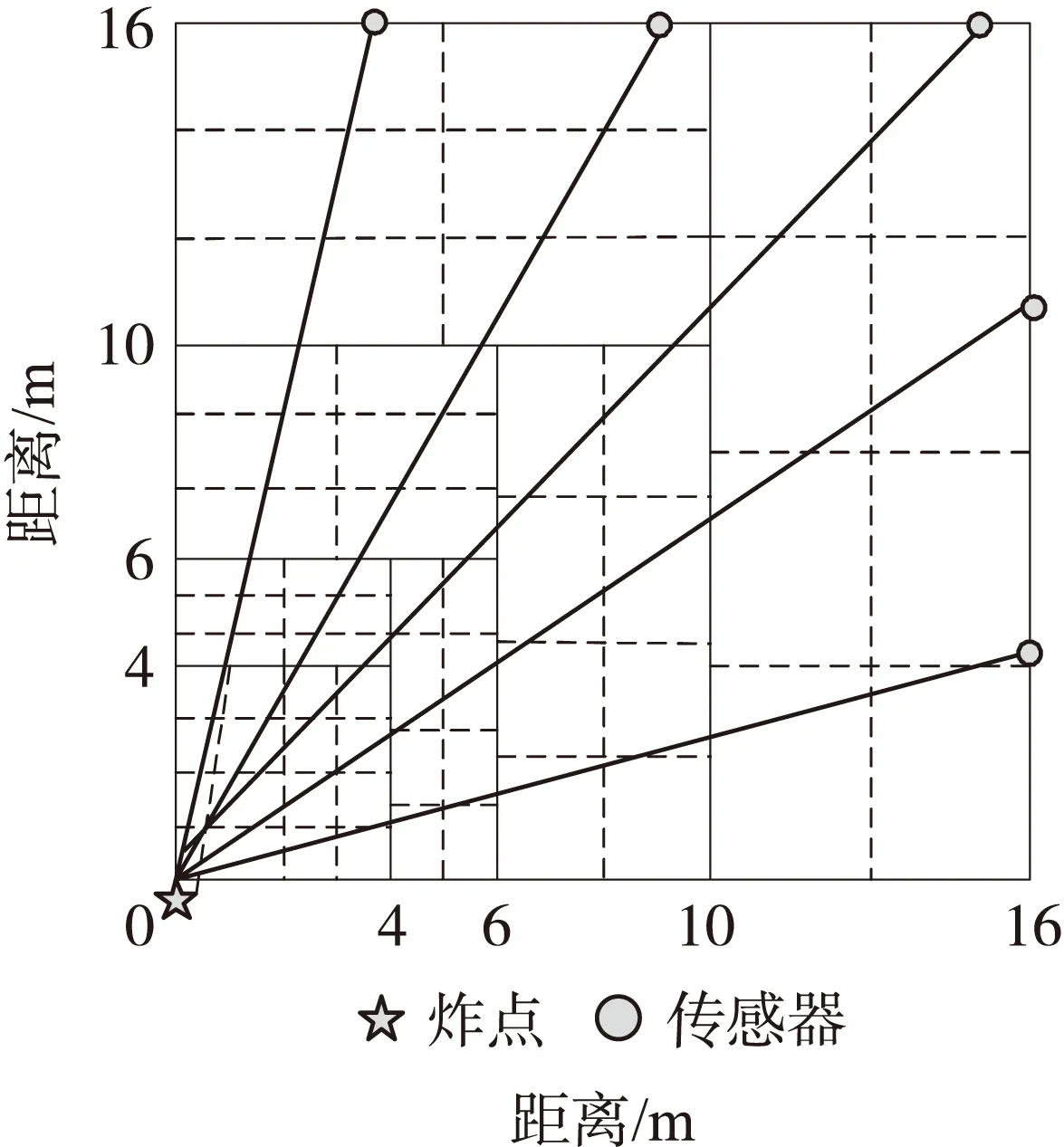
图5 不规则离散化模型

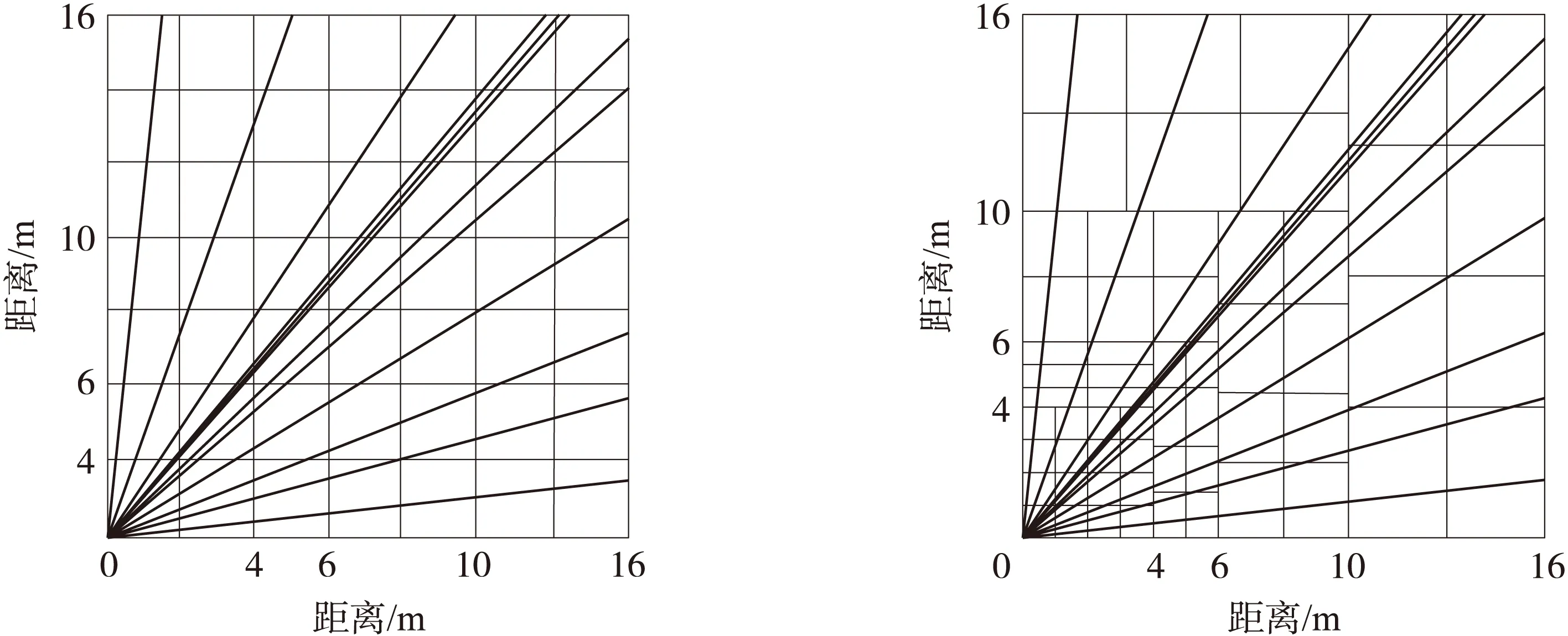
图6 同样数目的传感器在两种模型下的分布

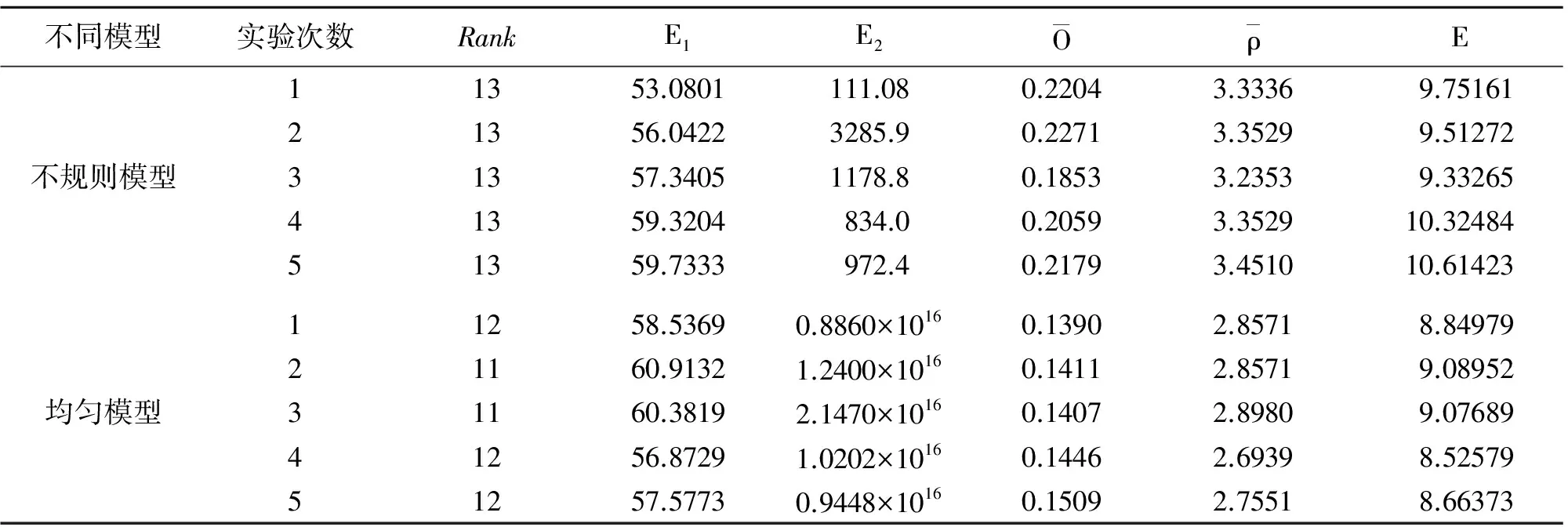
不同模型实验次数RankE1E2OρE11353．0801111．080．22043．33369．7516121356．04223285．90．22713．35299．51272不规则模型31357．34051178．80．18533．23539．3326541359．3204834．00．20593．352910．3248451359．7333972．40．21793．451010．6142311258．53690．8860×10160．13902．85718．8497921160．91321．2400×10160．14112．85719．08952均匀模型31160．38192．1470×10160．14072．89809．0768941256．87291．0202×10160．14462．69398．5257951257．57730．9448×10160．15092．75518．66373

2.3 传感器优化布局仿真

2.3.1 优化布局算法

对于层析成像观测系统,一条射线对应着一对发射和接收器的位置,优化射线分布,即是要优化发射器和接收器的布局,在本文中也就是优化爆炸点和传感器的位置。在离散模型一定的情况下,发射器和接收器的几何位置是影响矩阵D结构的主要因素。在给定发射器和接收器数量的情况下,采用优化算法,将评价函数作为目标函数,寻求发射器和接收器的最优几何分布。本文利用自适应粒子群[10-12]优化算法进行传感器优化布局,算法流程如下:

①在测试范围内,根据发射器和接收器数目,随机给出一种布局方式,即产生一个d维粒子,表示为a=(xs1,…,xsm1,ys1,…,ysm1,xr1,…,xrm2,yr1,…,yrm2)xsi和ysi分别表示第i个发射器的坐标,在本文中指中心炸点坐标;xri、yri分别表示第i个接收器,也就是本文的传感器坐标;d=2m1+2m2,m1和m2分别表示试验所用发射器和接收器数目;

②计算矩阵D,并逐一判断矩阵D的列向量是否为零向量;同时,计算矩阵D的秩;

③如果矩阵D的所有列向量都不为零向量,并且矩阵D是满秩的,则将该粒子加入粒子群;否则,放弃该粒子,返回①;

④粒子群数量达到所设定数量时,根据目标函数,计算群体和个体最优适应度值;

⑤更新粒子位置和速度,并把速度限制在c和vmin之间,计算适应度值;

⑥更新个体极值,对于每个粒子,将其适应度值与所经历过的最好位置的适应值进行比较,如果当前的适应度值比其历史最优值要好,那么历史最优将会被当前位置所替代;

⑦更新群体极值,对于每个粒子,将其历史最优适应度值与群体最优适应度值进行比较,如果该粒子的历史最优值比群体最优值要好,那么群体最优值将会被该粒子的历史最优值所替代;

⑧检查终止条件,终止迭代或返回⑤,重新计算。

2.3.2 仿真结果

建立如图5所示的不规则离散模型,随机选取13个传感器,根据E1、E2和E3数值大小,w1=0.8,w2=0.2,w3=15,k1=0.1,k2=0.9。采用粒子群优化算法,其各参数为:最大迭代次数q=100;初始化群体数目M=40;学习因子c1=2,c2=2;初始/终止惯性权重wmax=0.9,wmin=0.4;粒子最大更新速度为vmax=xmax-xmin,其中xmax和xmin为所求未知数上下界;粒子速度范围[-vmax/2,vmax/2],得到最佳评价函数E从而得到最佳射线分布。结果如表2所示。

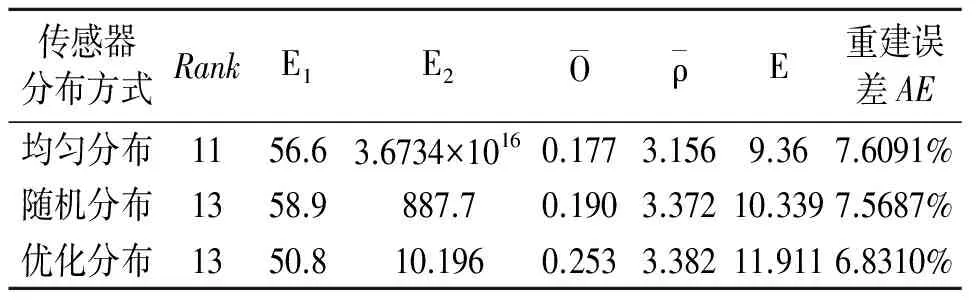
表2 各指标在不同射线分布下的比较

比较3种不同布局的传感器各指标特点,如表2所示,可以看出,采用本文提出的算法优化布局后,各项指标均优于其他分布,即优化布局后射线密度和射线正交性变大,指标E1和指标E2也有所改善,矩阵D的性质改善,从而所得重建误差减小。说明优化布局有一定的优越性,在实际试验中可以利用这种方案来指导传感器布局节省试验经费。

图7 传感器均匀分布

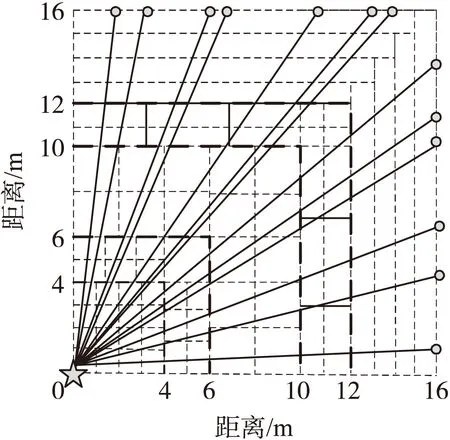
图8 传感器随机分布

图9 传感器优化分布

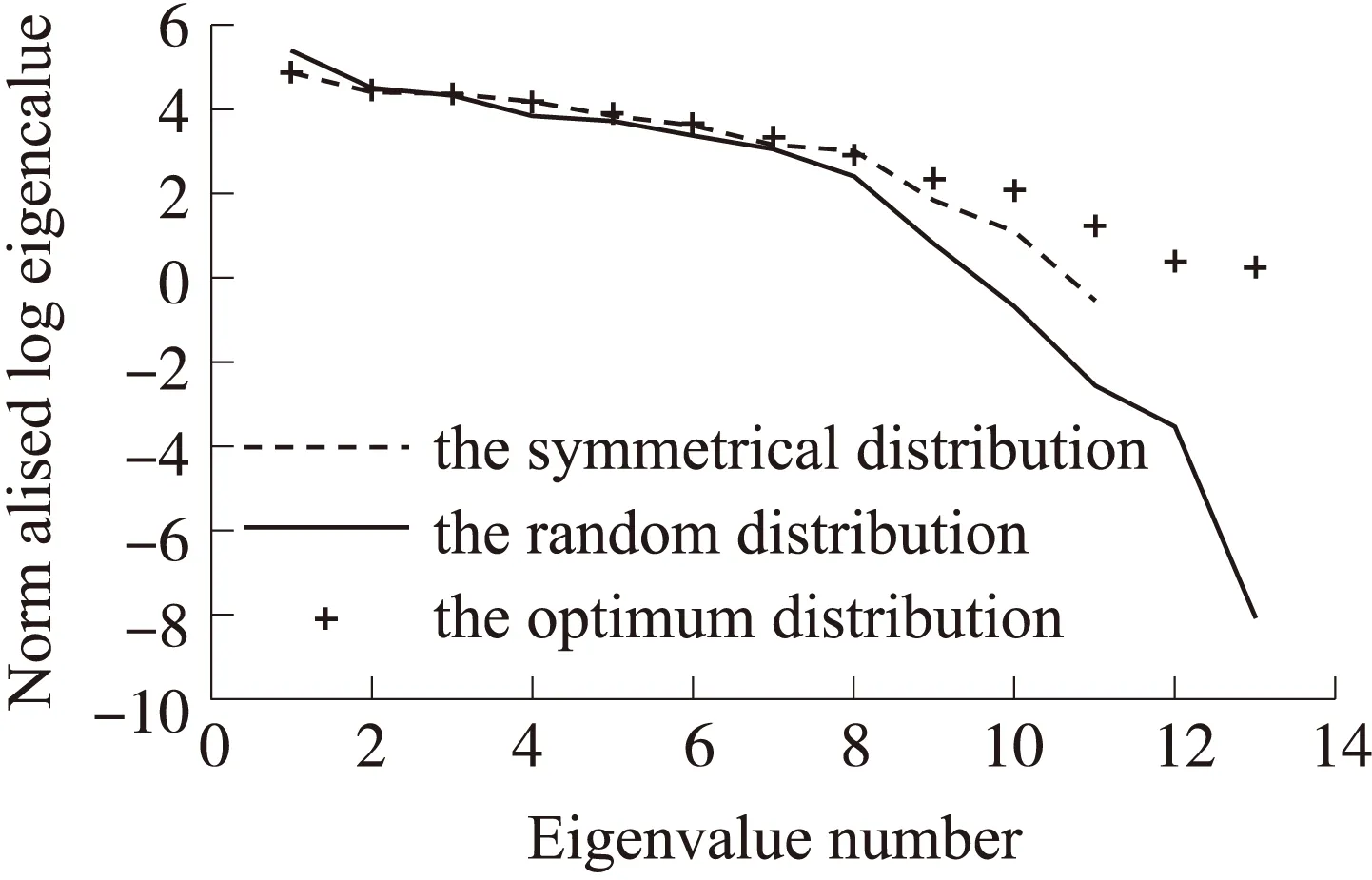
图10 不同布局下特征值分布

3 结论

首先,本文提出了一种地下爆炸超压场重建的方案,基于这种方案,我们从模型离散化和传感器优化布局两方面来进行爆炸层析成像信息优化获取技术研究,得出如下结论:

①不规则离散模型策略可以满足爆炸冲击波在近场、中场、远场的不同分辨率要求,抗干扰能力强,传感器利用率高。

②传感器布局时,尽量使得射线路径矩阵的秩越大越好、特征值越大越好、射线密度越大越好、射线正交性越大越好、条件数越小越好。

③重建精度很大程度上依赖于传感器布局方式,所以,实际试验中我们要采用优化布局算法指导实际传感器布放。节省试验经费。

[1] 邱艳宇,卢红标,蔡力艮. 爆炸冲击波信号处理方法比较[J]. 爆破,2010,327(1):92-95.

[2] 仲倩. 爆炸源毁伤效应测评方法研究[D]. 南京:南京理工大学,2007:7.

[3] 童平. 地震层析成像方法及其应用研究[D]. 北京:清华大学,2012.

[4] 李石坚,廖备水,吴健. 面向目标跟踪的传感器网络设计、实现和布局优化[J]. 传感技术学报,2007,20(12):2622-2630.

[5] 刘国华,王振宇,孙坚. 弹性波层析成像及其在土木工程中的应用[J]. 土木工程学报,2003,36(5):76-81.

[6] 成谷. 地震反射走时层析理论与应用研究[D]. 上海:同济大学,2004:6.

[7] Zolta′n We′ber. Seismic Traveltime Tomography:A Simulated Annealing Approach[J]. Physics of the Earth and Planetary Interiors,2000,119:149-159.

[8] 白苗苗,郭亚丽,王黎明. 基于爆炸超压场重建的传感器优化布局技术研究[J]. 传感技术学报,2014,27(7):886-892.

[9] 林大超,白春华. 爆炸地震效应[M]. 北京:地质出版社,2007.

[10] LanLan Zhen,Ling Wang,Xiuting Wang. A Novel PSO-Inspired Probability-Based Binary Optimization Algorithm[C]//Information Science and Engineering,2008. ISISE’08. International Symposium on. IEEE,2008:248-251.

[11] 高海兵,周驰,高亮. 广义粒子群优化模型[J]. 计算机学报,2005,28(12):1980-1987.

[12] 刘洪波,王秀坤,谭国真. 粒子群优化算法的收敛性分析及其混沌改进算法[J]. 控制与决策,2006,21(6):636-645.

白苗苗(1987-),女,甘肃庆阳人,研究生在读,研究方向为信号与信息处理、爆炸场重建、反演算法,baimiaomiao641@163.com;

王黎明(1974-),男,教授,博士生导师。主要从事X射线图像处理、多维信号获取与处理、无损检测技术等领域的教学和研究工作,wlm@nuc.edu.cn。

A Technology Optimizing the Information about ShallowUnderground Explosion*

BAIMiaomiao,WANGLiming*,GAORui,FANXuejun,WANGKe

(College of Communication and Information Technolgy,North University of China,Taiyuan 030051,China)

A technology of shock wave overpressure space-time field reconstruction about underground explosion was put forward,based on the theory of seismic tomography. In order to improve the underground explosion field tomography information effectively,the paper optimized imaging information from two aspects of model discretization and sensor layout. For discrete model,the irregular grid was adopted according to the attenuation rule of shock wave. For the sensor layout,according to the mathematical underdetermined problem theory and seismic wave propagation law,put forward the index and optimization algorithm for guiding the sensor layout,realize the rational layout of sensors. Simulation results show that,tomography information optimization extraction can maximize the utilization of data,which makes the inversion process is more stable,the inversion error is small.

sensor;optimized layout;seismic tomography;overpressure space-time field;underground explosion;

项目来源:国家自然科学基金项目(61471325)

2014-11-08 修改日期:2015-03-09

C:7230

10.3969/j.issn.1004-1699.2015.06.014

TP301.6

A

1004-1699(2015)06-0858-06