基于量子粒子群优化算法的压缩感知数据重构方法*

刘洲洲,李艳平

(1.西安航空学院,西安 710077;2.菏泽学院计算机与信息工程系,山东 菏泽 274015)



基于量子粒子群优化算法的压缩感知数据重构方法*

刘洲洲1*,李艳平2

(1.西安航空学院,西安 710077;2.菏泽学院计算机与信息工程系,山东 菏泽 274015)

针对传感器监测对象特点,将压缩感知理论应用于数据压缩过程以降低通信能耗,并根据现有压缩感知数据重构算法存在的重构精度受稀疏度影响较大的缺点,在分析了压缩感知数据重构原理后,提出了将原始信号按固定长度进行分帧处理以减少算法解空间的数量,并将量子理论中的编码方式应用于粒子群优化算法,提出了基于量子粒子群优化算法的压缩感知数据重构方法QP-CSDR。算法根据传感器监测对象特点,从统计学角度出发对粒子群优化算法中的粒子初始位置及粒子群更新方式加以改进,以提高数据重构精度。仿真实验结果表明,在稀疏度小于50的条件下,QP-CSDR算法相对已有算法在重构精度方面性能提升20%～40%,该算法已应用于微地震及音频监测系统中,经实际检验算法在保证数据精度的前提下延长系统寿命2倍～4倍左右。

量子理论;粒子群优化算法;压缩感知;数据重构

压缩感知是目前数据压缩的重点研究方向,能够以高压缩比对数据进行压缩,并通过数据重构算法对数据实现重构。国外对如何将压缩感知应用于无线传感器网络及相关数据重构方法进行了大量研究[1-2]。数据重构算法的关键问题在于如何快速的、准确的从已知的低维数据中恢复出高维数据。目前压缩感知数据重构算法主要分为两类[3]:第1类算法则是基于最小化l1范数的算法,包括基追踪算法BP(Basis Pursuit)[4],线性规划算法LP(Linear Programming)[5]等。这类算法具有重建精度高的优点,但其算法的复杂度较高,且执行效率低,使用性较差;第2类是基于最小化l0范数的方法,即贪婪算法,包括正交匹配追踪算法OMP(Orthogonal Matching Pursuit)[6]、正则化正交匹配算法ROMP(Regularized Orthogonal Matching Pursuit)[7]、压缩采样匹配追踪算法CoSaMP(Compressive Sampling Matching Pursuit)[8]、迭代硬阈值算法IHT(Iterative Hard Thresholding)[9]、基于感知字典的迭代硬阈值算法SDIHT(Sending Dictionary-based Iterative Hard Thresholding)[10]、基于混沌量子免疫克隆算法的正交匹配算法OMP-QICA(Orthogonal Matching Pursuit based on Quantum-inspired Immune Clonal)[11]、基于遗传算法的压缩感知重构算法[12]、稀疏度K自适应的稀疏自适应匹配追踪算法SAMP(Sparsity Adaptive Matching Pursuit)[13]等,这类算法主要通过迭代更新当前估计来优化信号恢复情况,在原始信号稀疏度较小的情况下具有很好的重构精度及重构速度,但对于稀疏度较高的信号重构问题却无能为力。

粒子群优化算法PSO(Particle Swarm Optimization)是目前国内外的研究热点[14-16],在问题寻优的过程中要比其他经典算法具有更好的优势及可行性,应用于N-P完全问题,PSO算法也取得了比以往算法更好的效果。尽管PSO算法具有自身的优势,但在实际应用中还是常出现陷入局部极值等现象。应用于压缩感知数据重构过程中常出现适应度较低但重构误差极大的情况。

针对这些不足,将量子免疫克隆理论带入粒子群优化算法,提出基于量子理论的粒子群优化算法QP-CSDR(Quantum-inspired immune clonal based Particle Swarm Optimization in Compressed Sensor Data Reconstruction)并将其应用于压缩感知数据重构过程中。旨在利用量子免疫克隆算法中的种群生成方法以及种群更新方法来实现种群扩张,为粒子群优化算法提供更广泛、更丰富的粒子位置,扩大了搜索空间,提高了局部搜索能力,避免算法陷入局部最优出现早熟现象。

1 数据重构算法

1.1 固定长度分帧

固定长度分帧方式就是将原始长信号按照固定的数据长度分为若干帧。假设信号采集端采集的原始信号长度为N,则按算法设定的帧长度n将原始信号分为frame=ceil(N/n)个帧,每个帧内包含的非零元素个数不等。举例说明:

假设原始信号x为:

0 0 0 1 1 1 0 1 0 1 0 1 0 0 1 0 0 0 1 0 1 1 0 1 0 0 1 0 0 0

其原始信号长度为30,按每帧长度为5个数据分帧,则可分为以下6个帧:

0 0 0 1 1 | 1 0 1 0 1| 0 1 0 0 1 | 0 0 0 1 0 | 1 1 0 1 0| 0 1 0 0 0

这种方法的特点是每帧的长度相同,而稀疏度不同。

(1)

则根据概率论相关知识可知:其重建概率为:

(2)

(3)

以上述数据为例,表1显示未分帧及分帧后的原始信号x中非零元素位置组合数量(为计算简便,这里假设数据为均匀分布):

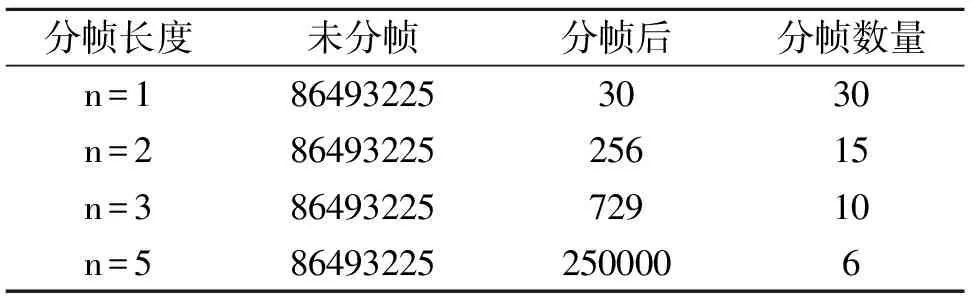
表1 固定长度分帧前后非零元素位置组合数量

可以看出,较短的分帧长度会降低组合数量,但在实际过程中会因为分帧长度过短导致帧数量增加,导致通信包数量急剧增加,提高了通信开销,造成网络拥塞,使分帧方法的实用性降低。而当n取值过大时,虽然能够减少通信包数量,降低通信开销,但也会造成非零元素位置组合数量急剧增加,降低了数据的重构概率。

1.2 改进的量子粒子群优化算法

假设初始状态下,PSO系统中的每个粒子的位置不能确定,每个粒子位置的量子位状态是随机的,可以为0或1,也可为0到1间的任意随机数,其状态表示为公式:

|Ψ〉=α|0〉+β|1〉

(4)

式中:α,β表示相应状态出现概率的两个复数,其关系为α2+β2=1。

具有m个量子比特位的粒子群可以描述为式(5):

(5)

式中:t表示种群代数。结合信号重构的应用实际考虑,m表示数据长度。规模为n的粒子种群表示为:

Q(t)={q1,q2,…,qn}

Q(t)即为信号重构的解空间。

从统计学角度看,传感器监测的物理对象特征多服从正态分布,因此在理论中不应当仅简单的假设为均匀分布,设其幅值xi∈[min,max],可设其位置的概率密度函数为式(6):

(6)

式中:αi为随机数,则粒子的初始化位置xi编码规则如式(7):

xi=0.5×[max(1+T(αi))+min(1-T(αi))]

(7)

粒子的当前最优位置Pi的更新及速度的更新方式与经典PSO算法中相应参数的更新方式完全相同,即:

(8)

(9)

式中:f(·)为目标函数,在数据重构算法中,将式(3)作为目标函数,通过不断生成解x并与压缩后数据Y进行比较,从而不断逼近原始数据。

量子粒子群算法中,当长时间搜索不到全局最优解时,种群需要进行更新,这里我们借鉴全干扰交叉操作。假设一个种群包含5个长度为8的抗体,其具体交叉方法见表2。

表2 全干扰交叉操作

下面给出基于QP-CSDR算法压缩感知数据重构方法的执行步骤。

1.3 数据重构过程

本文提出的基于量子粒子群优化的压缩感知数据重构算法流程图如图1所示。

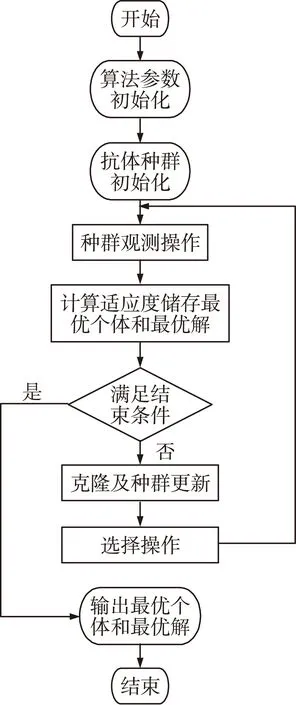
图1 算法流程图

算法具体过程如下:

①将原始数据按长度n进行分帧处理。通过遍历算法记录各帧稀疏度spratio;②在问题空间中,根据式(7)及原始信号稀疏度spratio初始化粒子群中各粒子的位置,使得粒子位置的稀疏度与原始信号稀疏度相同;③根据式(3)计算粒子的当前适应度,并与前一次迭代的适应度值进行比较,若当前适应度值小于前一次迭代的适应度值,则根据粒子的位置更新为粒子当前的最优位置;④根据式(9)计算群体当前的全局最优位置;⑤比较当前全局最优位置与前一次迭代的全局最优位置,若当前全局最优位置更好,则群体的全局最优位置更新为当前值;⑥根据式(8)、式(9)计算随机点的速度及新位置;⑦若迭代次数达到一定阈值后,适应度值仍未达到要求,则使用全干扰交叉方式,将粒子位置进行全局交叉,然后重新计算全局最优值及局部最优值;⑧重复步骤②～步骤⑥,直至满足一定的结束条件;⑨将所有重构信号按帧序列组合完整的重构信号。

2 实验及分析

试验场地选择在秦始皇帝陵博物院K9801号坑旁,监测对象为微地震信号。为使结果更加清晰,同一实验地点处布设两个硬件结构相同的无线传感器节点,一个传输未压缩信号,另一个传输压缩信号。将两类数据导入计算机,并通过MATLAB运行程序对重构的压缩信号进行评估,并同时监测节点的工作时长。

2.1 分帧结果分析

固定长度分帧的实验结果如图2所示。

图2 N=5时的数据重构结果

当N=5时,原始数据共分为40个帧,信号压缩比为200∶59,近乎达到3∶1。考虑通信中,每帧数据包需要额外增加2个字节原始帧长度和稀疏度信息,原始数据长度为400byte,压缩后数据长度为118byte,额外通信开销为80byte,实际数据压缩比率为198∶400=0.495。重建信号的精度为98.5%。可以看出,由于每个帧内仅有5个数据,因此其重构精度大大提高,QP-CSDR算法能够对数据进行高精度重构。但N=5时分帧数量过多,通信开销较大,因此实际应用中效果较差。

如图3所示,当N=10时,原始数据共分为20个帧,信号压缩比为200∶59,约为3∶1。原始信号长度为400byte,压缩后信号长度为118byte,考虑通信中,每帧数据包需要额外增加两个字节原始帧长度和稀疏度信息,额外通信开销为40byte,实际数据包长度压缩比率为158∶400=0.395。重建信号的精度为90%。可以看出,帧长度N=10时,算法的重构精度有所下降,主要是因为重构解空间数量较多,算法全局搜索能力下降所影响,N=10时的分帧数量有所减少,因此额外通信开销降低。

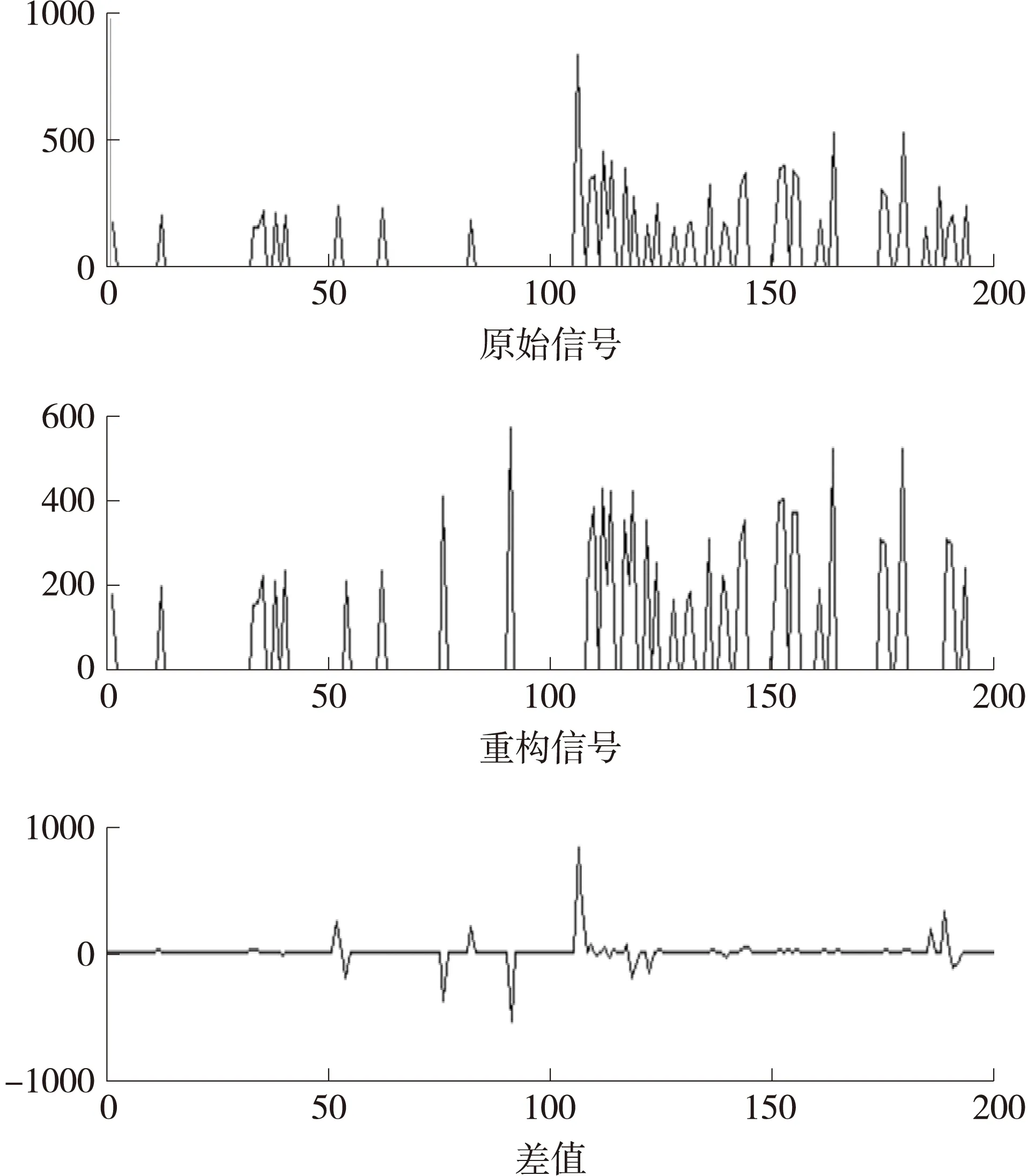
图3 N=10时的数据重构结果

如图4所示当N=20时,原始数据共分为10个帧,信号压缩比为200∶66,约为3.3∶1。考虑通信中,每帧数据包需要额外增加两个字节原始帧长度和稀疏度信息,额外通信开销为20byte,实际数据包长度压缩比率为142∶400=0.355。重建信号的精度为87%。可以看出,N=20时虽然额外通信开销很少,但其数据重构精度也随之下降,难以达到系统要求,因此实用性不高。

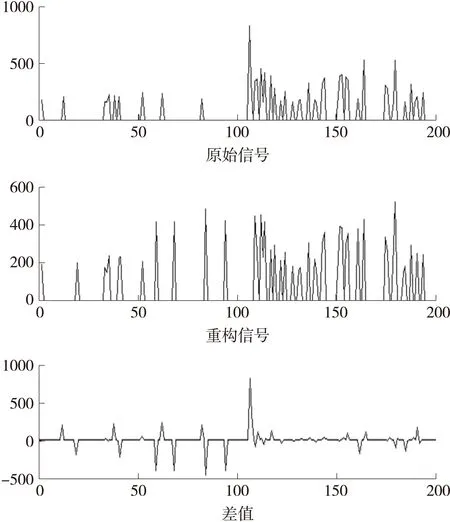
图4 N=20时的数据重构结果

2.2 同类算法对比分析

图5中显示的是在各稀疏度条件下,不同算法的性能对照(不考虑通信开销)。

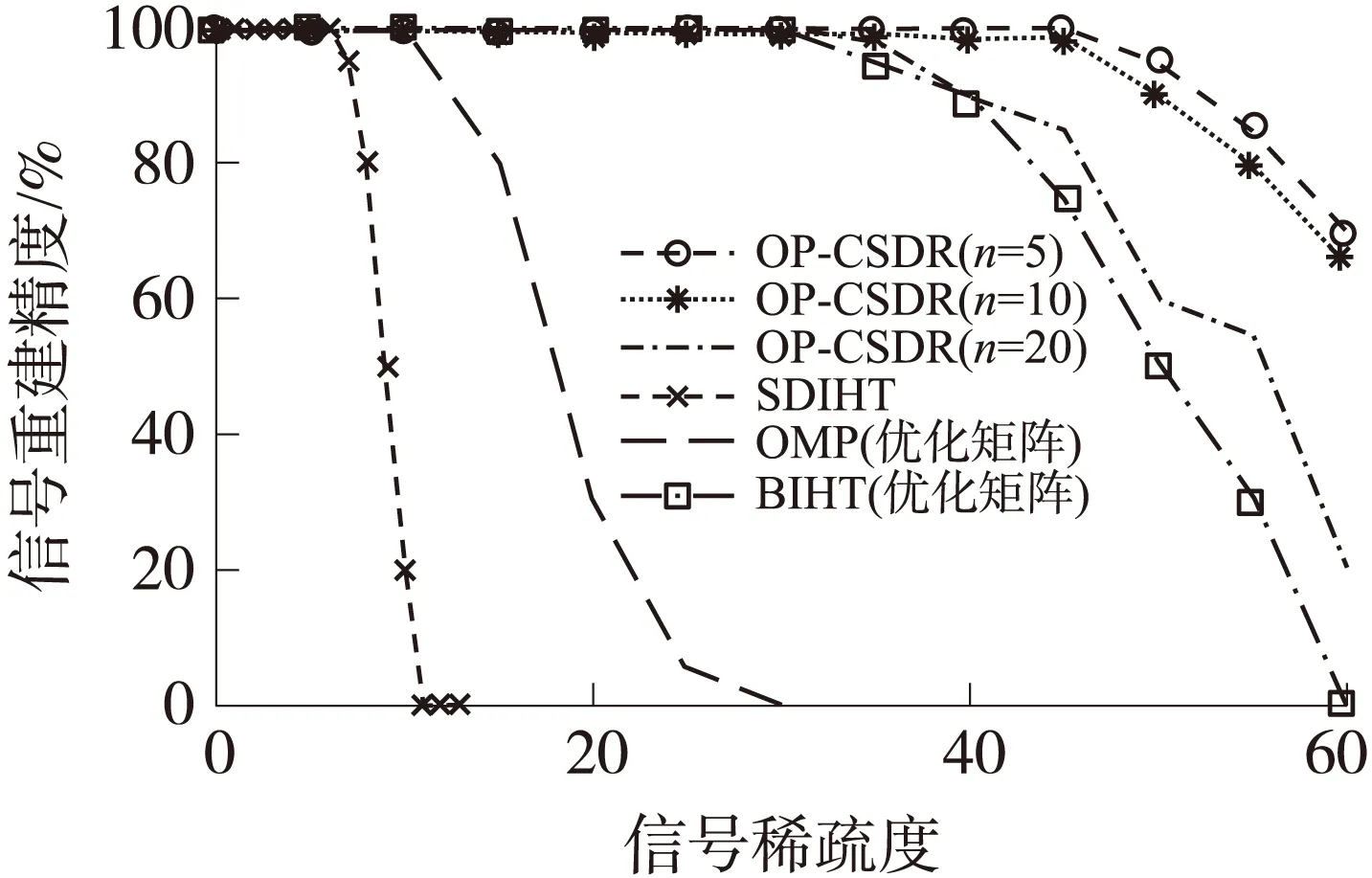
图5 同类算法实验结果对比

可以看出在稀疏度较小的条件下,各类算法都具有较好的数据恢复精度。而在稀疏度大于30后,OMP算法的数据恢复性能急剧下降,SDIHT及BIHT算法在稀疏度大于40后也出现了明显的下降趋势,而QP-CSDR算法在稀疏度大于45后出现明显下降,特别是n=5时的QP-CSDR算法在稀疏度50时仍能保持近90%的恢复概率,这也说明了分帧长度对于数据恢复精度的影响还是很明显的:分帧长度越短,解空间数量越少,数据重构精度越高,反之则解空间数量越多,数据重构精度越低。

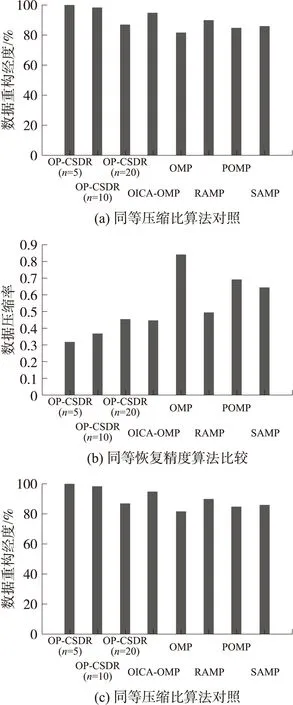
图6 同类算法实验结果对比

图6中显示的分别是针对稀疏度为0.2的原始信号,在压缩比率为0.3和重构精度为90%的条件下不同算法的性能对照(不考虑通信开销)。

可以看出在两种情况下,N=5时本算法的压缩比率和数据重构精度都是较高的。N=10时的算法性能与QICA-OMP和RAMP[12]算法相近。N=5时的算法性能与ROMP算法和SAMP算法差异不大,在压缩比率和数据重构精度方面都较OMP算法好。由于OMP算法本身具有重构精度不高的特点,因此在同等重构精度条件下性能不好,几乎以1∶1的方式才能对原始信号进行高精度重构。

2.3 网络实验性能结果

网络的性能结果如表3所示。监测对象为微地震信号及音频信号,采样速率分别为10sample/s和200sample/s.节点为不进行数据压缩的传感器节点及N=10时的固定长度分帧。两个传感器的采集速率均为10sample/s,每采集200个数据的时长为20s,均采用4 400mAh,3.6VDC的锂电池供电。发送能耗按照30μJ/bit计算,共计实验10组,统计其平均值。

微地震信号条件下,压缩后的传感器节点的通信能耗比未压缩之前降低了1/5,。而考虑到计算能耗,接收能耗以及待机能耗等因素,节点的实际寿命延长至3.69倍左右。

音频信号条件下,压缩后的传感器节点的通信能耗比未压缩之前降低了1/3左右。考虑到计算能耗等因素,节点的实际寿命延长至2倍左右,之所以小于微地震信号实验的原因在于音频信号处理所需的计算能耗更高。

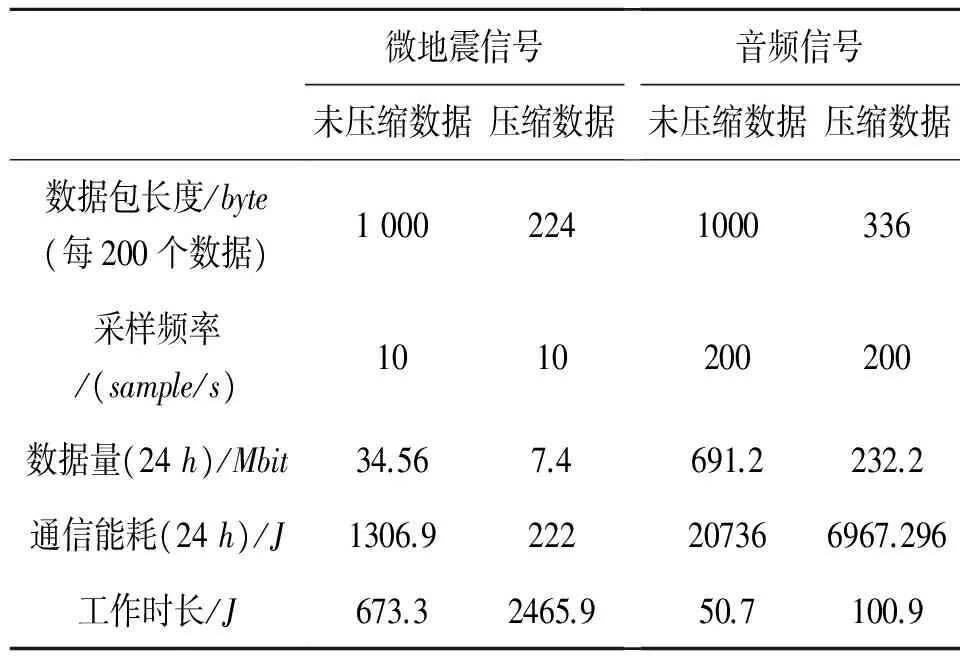
表3 微地震网络性能结果

3 结论

本文提出了基于量子粒子群优化算法的压缩感知数据重构方法QP-CSDR。文章首先针对压缩感知数据重构原理进行分析,提出将原始数据进行固定长度分帧,以减少重构空间解的数量,然后将粒子群优化算法应用于压缩感知数据重构过程中。在此基础上,根据网络监测对象的统计学特点对粒子群的粒子位置的初始化进行了改进,提高了各种稀疏度条件下的数据重构精度。实验结果表明,改进后的量子粒子群算法能够在稀疏度低于50的条件下以高精确度重构数据,与现有算法相比,重构精度提高10%～30%左右。实际实验结果表明,算法能够对传输数据进行高比例压缩,减少了通信数据量、降低了通信能耗,以微地震信号为检测对象时,系统寿命延长了3.7倍、以音频信号为监测对象时,系统寿命延长了2倍左右。

[1] Kaneko M,Al Agha K. Compressed Sensing Based Protocol for Interfering Data Recovery in Multi-Hop Sensor Networks[J]. IEEE Communications Letters,2014,18(1):42-45.

[2] Mecklenbrauker C F,Gerstoft P,Panahi A,et al. Sequential Bayesian Sparse Signal Reconstruction Using Array Data[J]. IEEE Transactions on Singal Processing,2014,61(24):6344-6354.

[3] Figueiredo M,Nowak R,Wright S. Gradient Projection for Sparse Reconstruction:Application to Compressed Sensing and Other Inverse Problems[J]. IEEE Journal of Selected Topics in Singal Processing,2007,1(4):586-597.

[4] Tropp J,Gilbert A. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J]. IEEE Transctions on Information Theory,2008,53(12):4655-4666.

[5] Needell D,Vershynin R. Greedy Signal Recovery and Un-Certainty Principles[J]. Proceddings of the Conference on Computational Imaging,2008:1-12.

[6] Needell D,Vershynin D. Uniform Uncertainty Principle and Signal Recovery via Regularized Orthogonal Matching Pursuit[J]. Foundations of Computational Mathematics,2009,9(3):318-334.

[7] D Needell R Vershynin. Signal Recovery from Incomplete and Inaccurate Measurements via Regularized Orthogonal Matching Pursuit[J]. IEEE Journal of Selected Topics in Processing,2010,4(2):310-316.

[8] 轩春青,轩志伟,陈保立. 基于最小二乘与粒子群算法的压力传感器动态补偿方法[J]. 传感技术学报,2014,27(10):1363-1367.

[9] 高伟,赵博,周广涛. 基于带约束人工蜂群算法和平均Hausdorff距离的重力匹配方法[J]. 传感技术学报,2014,27(1):74-78.

[10] Needell D,Tropp J A. CoSaMP:Iterative Signal Recovery from Incomplete and Inaccurate Samples[C]//ACM Technical Report 2008-01,California Institute of Technology,Pasadena,2008:93-100.

[11] 解志斌,于谦,沈斌,等. 一种新的基于粒子群优化的双簇头分簇路由算法[J]. 传感技术学报,2013,26(8):1135-1139.

[12] 刘亚新,赵瑞珍,胡绍海,等. 用于压缩感知信号重建的正则化自适应匹配追踪算法[J]. 电子与信息学报,2010,32(11):2713-2717.

[13] Tropp J,Lu Gan,Nam Nguyen,et al. Sparsity Adaptive Matching Pursuit Algorithm for Practical Compressed Sensing[C]//42nd Asilomar Conference on Signals,Systems and Computers,2008:581-587.

[14] Ho S L,Shiyou Yang,Guangzheng Ni,et al. A Quantum-Based Particle Swarm Optimization Algorithm Applied to Inverse Problems[J]. IEEE Transactions on Magnetics,2013,49(5):2069-2072.

[15] Hirano H,Yoshikawa T A Study on Two-Step Search Based on PSO to Improve Convergence and Diversity for Many-Objective Optimization Problems[C]//IEEE Congress on Evolutionary Computation,2013:1854-1859.

[16] 刘美,徐小玲,黄道平. 应用粒子群优化分配WSN多目标跟踪节点任务[J]. 传感技术学报,2010,23(9):1334-1339.

刘洲洲(1981-),男,山西运城人,博士研究生,讲师,2004、2007年于西北工业大学获得学士、硕士学位,主要从事无线传感器网络方面的研究,liuzhouzhou8192@126.com;

李艳平(1976-),女,山东郓城人,工学硕士,讲师。主要研究方向为智能算法,lyp5506@126.com。

Perceptual Data Reconstruction for Compressed Sensing Based onQuantum Behaved Particle Swarm Optimization*

LIUZhouzhou1*,LIYanping2

(1.Xi’an Aeronautical University,Xi’san 710077,China;2.Department of Computer and Information Engineering,Heze University,Heze Shandong 274015,China)

According to wireless sensor network monitoring object features,the compressed sensing theory is applied to data compression to reduce the communication energy. Considering that reconstruction accuracy of existing data reconstruction in compressed sensing can be easily influenced by sparsity,after analysis of compressed sensing data reconstruction principle,with sub-frame processing the original signal in fixed length to reduce the solution space,and applying quantum theory encoding in Particle Swarm Optimization,Compressed Sensing Data Reconstruction that based on Quantum-behaved Particle Swarm Optimization appears. According to wireless sensor network monitoring object features,this algorithm improves the accuracy of the data reconstruction by improving particle initial position and update mode in Particle Swarm Optimization from Statistics. Simulation results show that under conditions of sparsity less than 50,QP-CSDR gets 20%～40% performance improvement on Reconstruction accuracy comparing to existing algorithms. Now the algorithm has been applied to micro-earthquakes and audio monitoring system,and in actual inspection,the actual system life is extended about 2～4 times with assurance data accuracy.

wireless sensor network;quantum theory;particle swarm optimization algorithm;compressed sensor;data reconstruction

项目来源:国家自然科学基金项目(No.61103242)

2014-07-29 修改日期:2015-02-05

C:7230

10.3969/j.issn.1004-1699.2015.06.011

TP393

A

1004-1699(2015)06-0836-06