无解调电阻抗成像方法研究*

陈晓艳,杨永政,杜 萌

(天津科技大学电子信息与自动化学院,天津 300222)



无解调电阻抗成像方法研究*

陈晓艳*,杨永政,杜 萌

(天津科技大学电子信息与自动化学院,天津 300222)

探讨了正交序列数字解调算法中参考信号与测量信号频率不一致引起的解调结果不准确影响成像质量的问题,提出无需数字解调直接提取幅值进行电阻抗成像的方法:通过多次采样比较和算术平均滤波法获取幅值进行EIT成像。通过构建以FPGA为核心控制器的EIT系统,验证了直接提取阻抗幅值方法的可行性。实验结果表明:系统测量精度达0.082%,信噪比为60.3 dB,能准显示物体的大小和位置,空间分辨率达到0.29%,验证了方法的可行性,提高了数据采集精度和系统的稳定性,改善了图像成像质量,该方法为EIT技术的完善及系统性能的提升提供了一种有效的解决方案。

电阻抗成像;幅值提取;数字解调;FPGA控制器

电阻抗断层成像EIT(Electrical Impedance Tomography)是近40年发展起来的新一代无损伤医学成像技术[1-5]。根据被测区域的电阻抗特性,通过在体表面施加安全交流电流/电压,测量表面携带丰富信息的电压,以少量边界测量信号经电学断层图像重建算法重构被测对象内部电阻抗分布图像。由于电阻抗断层成像技术不使用超声、射线、电磁波等对人体无伤害,并且可以多次不间断测量、重复使用,成本低廉,成为一种理想的无损伤医学成像技术。EIT技术起源与1978年英国谢菲尔德大学,以人体手臂电阻抗图像而引人关注,迅速在全球范围内掀起高潮。从上世纪80年代发展至今全球已有80多个研究小组,许多研究小组都开发了自己独特的硬件系统。如Khan S、Borsic A等利用NI高性能的控制器板卡、激励板卡、采集板卡等搭建的高速数据采集EIT系统[6];Ryan J Halter、Alex Hartov等利用DSP和FPGA构建了64通道的EIT系统[7];Nicolas Robitaille、Robert Guardo等构建了一套基于无线电通讯信号处理器的多频EIT系统[8];Hun Wi,Harsh Sohal等利用DSP和FPGA构建的带有自校准输出电流的可进行长期监测的多频EIT系统[9],等等。然而,大多数硬件系统对于测量到的数据均采用模拟解调或正交序列数字解调的方式得到信号的幅值信息。

模拟解调的测量精度易受参考信号和正交参考信号的幅值及它们之间相位差的影响,数字解调能够克服参考信号与被测信号相位差的影响,但其对被测信号与参考信号的频率要求比较严格,任何微小的偏差都可导致幅值较大的变化。本文首先分析了正交序列数字解调方法在参考信号与测量信号频率不一致时,阻抗幅值存在的不准确原因,并提出采用直接提取阻抗信息幅值的方法进行成像。研究了频率差对于幅值计算的影响,从理论上解释了频率差造成的原因,最后通过试验证明了直接提取幅值的可行性及电极自诊断的必要性。

1 原理

1.1 直接提取幅值方法

在广泛采用的正交序列解调方法中,假设参考信号的频率和测量信号的频率一致,正交序列解调算法如下,设:

r(n)=cos(2πn/N)

(1)

q(n)=sin(2πn/N)

(2)

u(n)=Acos(2πn/N+θ)

(3)

式中:r(n)为同相参考信号,q(n)为正交参考信号,同时为EIT系统的激励源信号,u(n)为EIT系统中测量电极上的测量信号,θ为介质引起的相移,N为一个信号周期的采样数,n的取值范围为0≤n≤N-1,根据正交序列解调算法可计算实部分量R和虚部分量I。

(4)

(5)

因为参考信号和被测信号是同频,整周期相位是2π,参考信号和被测信号均匀采样N个点,所以

(6)

(7)

则

(8)

从而,幅值和相位可表示为:

(9)

当参考信号与测量信号的频率不一致时,参考信号一个整周期相位仍为2π,而测量信号因频率的变化导致均匀采样N个点时,对应的相角以小偏差偏离2π,设其为2π+φ,通常(-π/2<φ<π/2),则测量信号u′(n)可表示为:

u′(n)=Acos(2πn/N+φn/N+θ)

(10)

根据正交序列解调算法得实部分量R′和虚部分量I′如下:

(11)

(12)

可以看出因频率不同引起的N个采样点对应的相位偏差φ,严重影响了实部分量和虚部分量,因此,对于利用阻抗幅值成像的EIT系统而言,采用正交序列数字解调会引起较大的测量误差,从而影响成像质量。

本文提出直接提取幅值法,避免了正交序列解调的弊端而无需考虑参考信号和测量信号的频率差问题。其基本原理是:根据采样频率,在测量电极上等间隔采集N个点,只要参考信号和激励信号的频率差φ满足-π/2<φ<π/2,可采集到最大幅值Vmax和最小幅值Vmin,即可根据幅值A=Vmax-Vmin,直接计算获取测量幅值。可适当多次采样,并通过数字滤波算法即可提高测量数据的准确性。

2 EIT系统

为验证上述方法的可行性,构建了16电极EIT系统,硬件结构采用模块化设计,包括电源模块、以FPGA为控制核心的激励和采集模块及多路复用器模块,这3个模块都装配到一个母板上通过串口与上位机进行通信。利用LabView编写的上位机界面负责用户指令的发送和接收上传数据并将采集到的数据进行处理后进行实时成像。系统原理如图1所示。

图1 EIT系统的原理框图

2.1 硬件设计

电源模块是影响整个系统的关键因素之一,信号回路中的各种运放对电源的噪声都是非常敏感的,直接影响到信号的质量。因此本系统对电源模块进行了特殊的设计,利用Buck型拓扑结构及InvertingBuck拓扑结构电路实现DC+18V降压为±13V。利用LDO线性稳压技术得到纹波较低的纯净电源±DC12V,±DC5V。采用TI的电源管理芯片TPS75003得到FPGA所需的电压+1.2V、+2.5V、+3.3V。电源模块的实现在前期发表论文进行详细描述[10]。

图3 系统控制流程图

激励源的质量也是影响EIT系统测量精度的主要环节。利用FPGA自带的DDS(Direct Digital Synthesizer)IP核,对其进行相应的配置使其产生频率为100KHz,相位为0的数字正弦信号。经过数模转换器和低通滤波器就得到了比较纯净的正弦电压信号[11],再通过增强型的Howland电流源拓扑结构—电压控制电流源(VCCS)得到恒流源,本设计通过调节回路中的运放使输出电流为4 mA,输出阻抗为260 kΩ,EIT系统硬件如图2所示。

图2 EIT系统实物图

2.2 软件流程

系统主程序采用VHDL语言完成各元件信号的物理连接,利用FPGA片上嵌入的PicoBlaze微处理器完成数据采集过程的串行时序控制,利用FPGA片上的DCM(Digital Clock Manager)IP核得到3种性能稳定的50 MHz、125 MHz、5 MHz时钟频率。

软件控制流程如图3所示。上位机利用LabVIEW编写人机交互应用程序。首先检测所有电极确保接触良好,然后发送“HOMO”指令,按照相邻激励相邻测量的方式,采集均匀场数据并存入LabVIEW数据库,最后发送“INHOMO”指令,采集被测数据,其流程和空场的数据采集流程一致,直到收到停止采集指令。

3 实验与结果

3.1 方法验证

首先,在MATLAB软件平台进行仿真验证。设A=0.5,φ=0.05π,θ=0,N=100,代入式(3)和式(10),分别进行正交序列解调,得到频率一致时测量信号u,解调后的实部R和虚部I,以及频率不一致时测量信号u′,解调后实部R′和虚部I′,如图4所示。

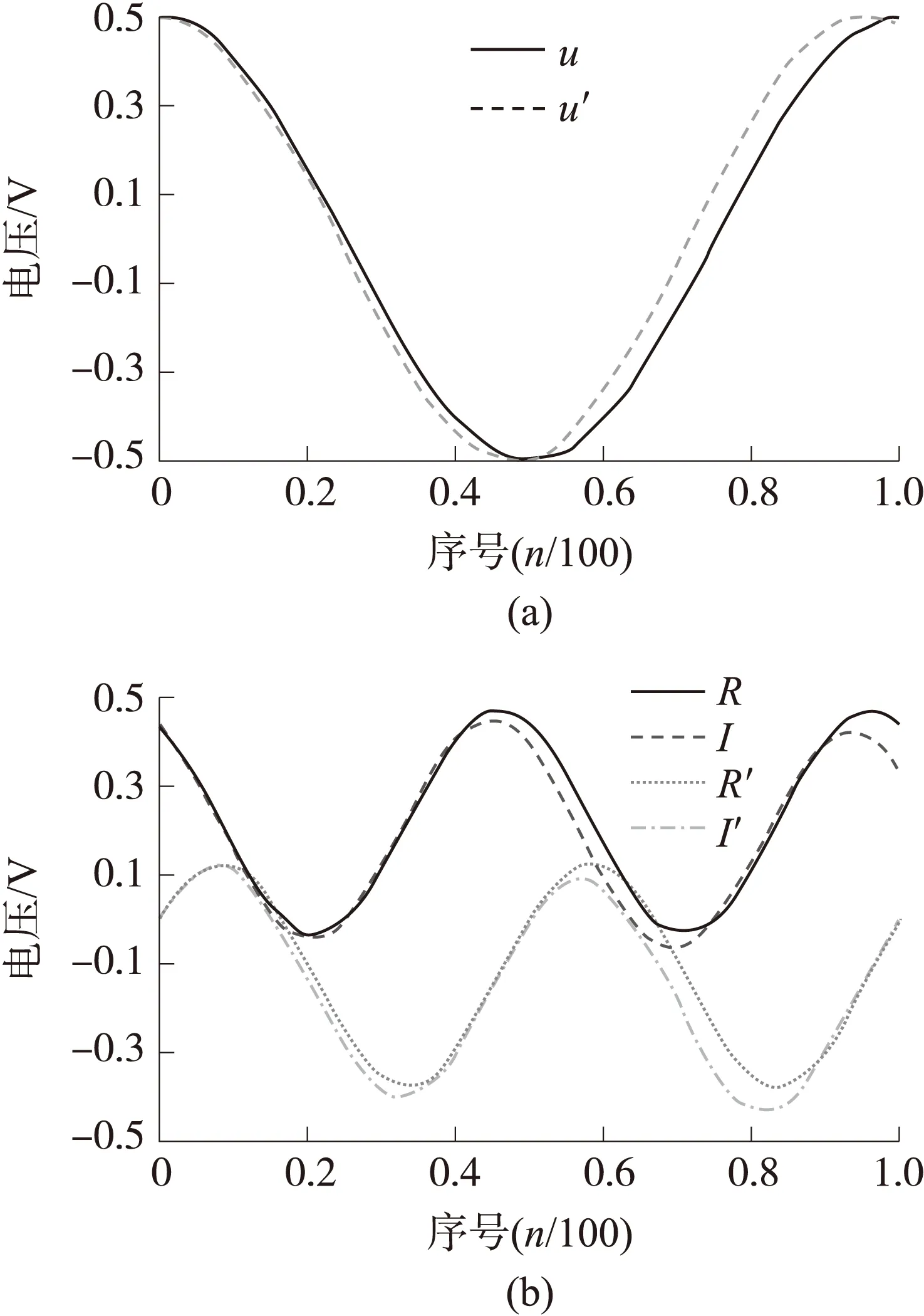
图4 两种不同频率的信号及对应的实部和虚部

图4(a)实线显示的是频率相同时测量信号u,虚线显示频率不同时的测量信号u′,图4(b)显示了因频率不同导致解调结果中实部R(细实线)和R′(细虚线)和虚部I(粗实线)和I′(粗虚线),由图可见,解调结果差异明显。为了进一步验证频率差对幅值的影响,设φ从-0.4π到0.4π每次间隔0.1π进行了正交序列解调计算,结果如表1所示。

表1 频率偏差程度对幅值计算的影响

由表1可知,解调误差随|φ|增大而变大,即当参考信号与测量信号的频率相差越大,采用正交序列解调的结果越不准确。

为了验证直接提取幅值方法的可行性和准确性,根据采样频率,等间隔采集50个点,经比较获得最大值Vmax和最小值Vmin,根据A=Vmax-Vmin,从而得到幅值A;依此连续采集5个周期,然后对5个幅值进行排序,去掉最大和最小值,采用算术平均滤波法将中间3个幅值的平均值作为这一个测量点的最终幅值。

为了进一步在实验装置上进行方法验证,对一组数据连续测量100次,计算相对误差和信噪比

(13)

(14)

图5 不同直径目标棒在盐水槽同一位置的成像效果

3.2 图像重建实验

3.2.1 静态成像实验

在直径为186mm的盐水槽中,盐水电导率为3.36ms/cm,距离槽边界20mm处,放置直径不同的棒,如图5(a)所示。目标棒是圆形有机玻璃棒,其电导率近乎为0,直径依次为50mm、40mm、30mm、20mm、10mm,利用共轭梯度成像算法[13],得到如下5幅图像见图5(b)～5(f)。

图中d表示有机玻璃棒的直径。由图5可以看出:当棒的直径缩小至d=10mm时,仍可辨识。

(15)

此时按面积比式(1)可计算空间分辨率达0.29%。其中S棒是目标棒的横截面面积,S槽是水槽的横截面面积。

为了进一步验证系统的稳定性和方法的可行性,对多个物体进行成像,如图6所示。

图6 多个物体的图像重建

图6(a)、(b)、(c)分别表示桶中不同位置不同直径的有机玻璃棒实际分布,对应的成像效果如图6(d)、(e)、(f)所示,由图可知本系统成像效果较为理想。

3.2.2 动态成像实验

在图6(a)所示的圆桶内,直径为30 mm的有机玻璃棒以8 rad/s的速度按顺时针方向匀速转动一周。其动态成像结果如图7(a)～7(e)所示,其中蓝色区域代表有机玻璃棒。通过这8幅图像基本可以反映有机玻璃棒的运动过程。

图7 动态性能测试

由成像结果可以看出,采用本文提出的改进方法构建的EIT系统,运行稳定,数据可靠,图像质量较课题组前期研制系统有明显改善。

4 结论

本文通过理论公式推导论证了正交序列数字解调中参考信号和测量信号频率不一致会导致解调结果不准确的问题,提出了直接提取幅值方法并对其原理进行了详细的阐述,通过模型试验验证了直接提取幅值的可行性和数据的准确性,将平均测量误差减小至0.082%,比正交序列解调方法有了显著提高,同时增强了测量的稳定性。能够对待测区域中目标的个数、大小、位置进行准确判断,并且对待测区域中目标物体的运动状态进行准确识别。本系统实现成像速度达60 s/frame,系统空间分辨率达到0.29%,系统信噪比为60.3 dB,EIT系统性能良好,提供了简单、直接、有效的解决方案。

[1] Brown B H,Barber D C,Seagar A D. Applied Potential Tomography:Possible Clinical Application[J]. Clin Phys Physiol Meas,1985(6):109-121.

[2] Brown B H. Electrical Impedance Tomography(EIT):A Review[J]. Med Eng Technol,2003,27(3):97-108.

[3] Nebuya S,Noshiro M,Yonemoto A,et al. Study of the Optimum Level of Electrode Placement for the Evaluation of Absolute Lung Resistivity with the Mk3.5 EIT System[J]. Physical Measurement,2006,27:S129-S137.

[4] Chen Xiaoyan,Wang Huaxiang,Zhao Bo,et al. Lung Ventilation Functional Monitoring Based on Electrical Impedance Tomography[J]. Trans Tianjin Univ,2009,15:7-12.

[5] Li Peng,Fang Xi,Chen Zipeng. Wireless Distributed Data Acquisition System for EIT[J]. Applied Mechanics and Materials,2014,490-491:1298-1301.

[6] Khan S,Borsic A,Manwaring P,et al. FPGA Based High Speed Data Acquisition System for Electrical Impedance Tomography[J]. Phys:Conference Series,2013,434:012081.

[7] Halter R J,Hartov A,Paulsen K D. A Broadband High-Frequency Electrical Impedance Tomography System for Breast Imaging[J]. IEEE Trans Biomed Eng,2008,55(2):650-659.

[8] Nicolas Robitaille,Robert Guardo. A Multifrequency EIT System Design Based on Telecommunication Signal Processors[J]. IOP Publishing,Physiol Meas,2009,30:S57-S71.

[9] Wi H,Sohal H,McEwan A Let al. Multi-Frequency Electrical Impedance Tomography System with Automatic Self-Calibration for Long-Term Monitoring[J]. IEEE T Biomed Circ S,2014,8:119-128.

[10] Guo Yanyan,Chen Xiaoyan,Yang Yongzheng. A Low Noise Power Design for Electrical Impedance Tomography System[J]. Applied Mechanics and Materials,Applied Mechanics,Materials and Manufacturing IV,2014,670-671:1159-1162.

[11] 苏凯麒,邹摇玲,王摇琴. 基于细胞阻抗传感器的腹泻性毒素检测系统设计与实现[J]. 传感技术学报,2014,27(3):283-288.

[12] Wu Jiani,Chen Xiaoyan,Ding Zhonglin. Digital Biomedical Electrical Impedance Tomography Based on FPGA[J]. Journal of Biosciences and Medicines,2013(1):14-18.

[13] 孙金秋,游有鹏,傅忠云. 基于共轭梯度法和互补滤波相结合的姿态解算算法[J]. 传感技术学报,2014,27(4):524-528.

陈晓艳(1973-),女,教授,博士,硕士研究生导师,主要研究方向为电学参数检测与处理,cxywxr@tust.edu.cn;

杨永政(1988-),男,硕士,主要研究方向为电阻抗成像技术,yyz1988@163.com。

Non-Demodulation Method Study for Electrical Impedance Tomography*

CHENXiaoyan*,YANGYongzheng,DUMeng

(College of Information and Automation,Tianjin University of Science and Technology,Tianjin 300222,China)

A problem is analyzed related to quadrature sequences digital demodulation algorithm due to frequency difference exists between reference signal and measured signal which can cause inaccuracy of data and sacrifice the image quality. An approach solving the problem is proposed based on extracting impedance amplitude directly by multiple samplings and taking the arithmetic average value for imaging by electrical impedance tomography(EIT). An EIT system based on FPGA is developed to verify the feasibility of extracting impedance amplitude directly. The experimental results indicate that the average accuracy of the EIT system can reach 0.082% and SNR(signal to noise ratio)is 60.3 dB and it can image out the correct rods with accurate size and location,the spatial resolution can reach 0.29%,which demonstrate the methods feasible and reliable. The accuracy and stability of the system are increased and the image quality is improved. Non-demodulation and self-diagnosis methods provide effective solutions for EIT system and can boost of the EIT technology application.

electrical impedance tomography;amplitude extraction;digital demodulation;FPGA controller

项目来源:国家自然科学基金项目(61301246);天津市应用基础及前沿技术研究计划项目(12JCYBJC19300)

2014-12-10 修改日期:2015-03-03

C:7230

10.3969/j.issn.1004-1699.2015.06.016

TP212.14

A

1004-1699(2015)06-0870-06