基于MVRVM回归和RVM二叉树分类的自确认气动执行器故障诊断算法*

冯志刚,王 茹,田 丰

(沈阳航空航天大学自动化学院,沈阳 110136)



基于MVRVM回归和RVM二叉树分类的自确认气动执行器故障诊断算法*

冯志刚*,王 茹,田 丰

(沈阳航空航天大学自动化学院,沈阳 110136)

为了解决自确认气动执行器的故障诊断问题,提出了一种基于多变量关联向量机(MVRVM)回归和关联向量机二叉树分类的气动执行器故障诊断方法,该方法利用多变量关联向量机回归建立气动执行器的正常模型,然后将实际输出与模型输出比较,产生残差作为气动执行器的非线性故障特征向量。以残差作为输入建立关联向量机二叉树多分类机,诊断气动执行器故障类型。利用DABLib生成的故障数据对所研究方法进行了验证,并与基于RVM一对一分类的故障诊断方法进行了比较,结果表明该方法是解决气动执行器故障诊断的小样本和非线性问题的一种有效方法。

自确认气动执行器;关联向量机;多变量关联向量机回归;RVM二叉树分类;RVM一对一分类;故障诊断

由于工业的飞速发展和工业自动化程度的日益提高,执行器作为工业过程中重要的技术设备,被人们广泛应用。而执行器根据其动力能源形式可分为气动、液动、电动3类[1]。气动执行器由于价格低廉、驱动能源易得、易于清洁、易于维护、响应速度快、防爆等优点被广泛应用,通常用于控制液体、气体和泥浆的流量。由于大多数执行器都工作在高温、高压、强干扰、强腐蚀等恶劣的环境下,其能否正常工作直接关系到生产的安全性和可靠性[2]。但对于诊断其故障还存在一些问题,例如:故障与系统有关,不同的系统要不同的方法诊断;很难分清故障是系统故障还是执行器的故障等。基于这些问题,1999年牛津大学控制工程研究室的学者在自确认传感器技术研究的基础上,将自确认SEVA(self-validating)技术应用于执行器,提出了自确认执行器(self-validating actuator)的概念[3-4],开创了一种新型的执行器研究方向——自确认执行器技术,这对执行器的发展必将成为一个非常重要的方向。本项目组通过对传统三组件式气动执行器进行改进,提出了一种自确认气动执行器,该种执行器不仅能够给出正确的控制输出,同时能够实现故障的自检测、自诊断,给出输出控制量的准确度信息,自身的工作状态信息等参数。其中对自身故障的检测和诊断是至关重要,为了解决气动执行器的故障诊断问题,目前主要采用的方法是神经网络方法[5-6]和支持向量机[2]方法,均取得了一定的效果,但是神经网络方法存在结构确定难、容易陷入局部最优、过学习问题且需要大量训练样本的缺点。支持向量机方法在很大程度上克服了神经网络的缺点,能够在一定程度上解决故障诊断的小样本、非线性问题,但是其在实际应用中也存在一些缺点:①核函数必须满足Mercer条件;②支持向量机具有一定的稀疏性,但是支持向量数会随着训练样本数的增加线性增加;③需要对一些模型参数进行优化,如果这些模型参数取值不当,将大大影响其性能,从而增加额外的计算量。

为了克服以上缺点,本文将基于贝叶斯概率框架理论的关联向量机用于气动执行器的故障诊断,提出了一种基于多变量关联向量(MVRVM)回归和关联向量机二叉树分类的气动执行器故障诊断方法。首先用MVRVM回归对无故障气动执行器的输入、输出进行建模,然后将实际输出和模型输出进行比较产生残差,如果残差发生异常则检测到故障,将残差作为特征向量输入到训练好的RVM二叉树多分类器,判断气动执行器的故障类型。基于MVRVM回归和关联向量机二叉树多分类的气动执行器故障诊断方法的原理如图1所示。

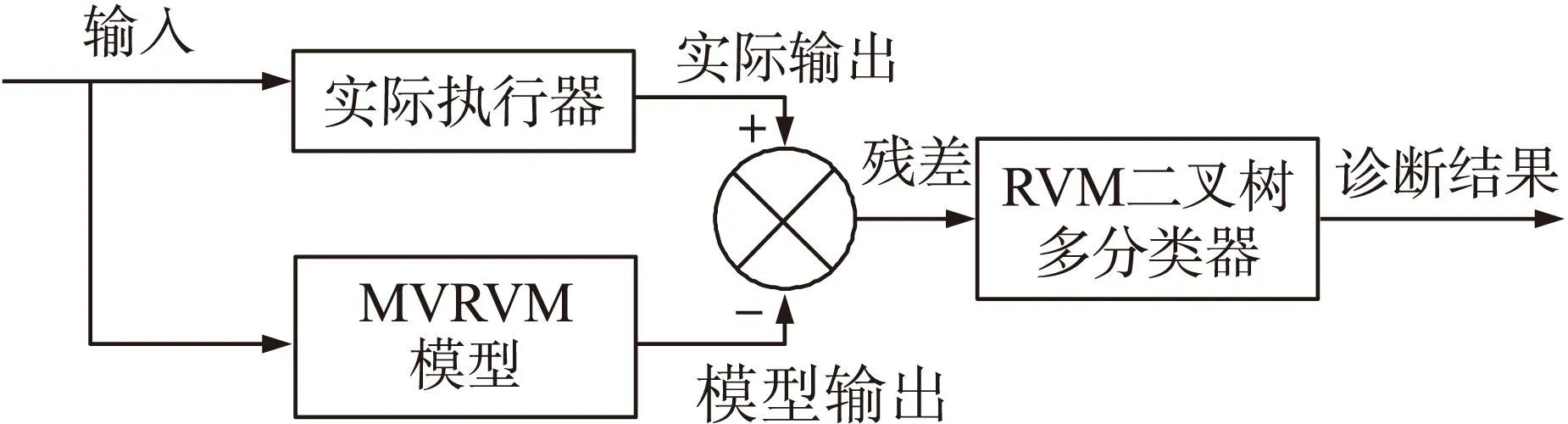
图1 基于MVRVM回归建模和RVM二叉树多分类器的气动执行器故障诊断方法原理

1 自确认气动执行器结构及常见故障

本文研究三组件式自确认气动执行器,由气动执行机构(Pneumatic servo motor)、阀门定位器(Positioner)、调节阀(Valve)3部分组成,如图2和图3所示。

图2 传统三组件式气动执行器结构图

图3 自确认气动执行器基本结构图

由图可知,自确认气动执行器是一个四输入,二输出系统,具体如图4所示,其中CV为阀位指令信号,P1为执行器阀体前流体压力,P2为执行器阀体后流体压力,T1为执行器阀体流体温度,是四个输入;X为位置反馈信号,F为流量信号,是两个输出。

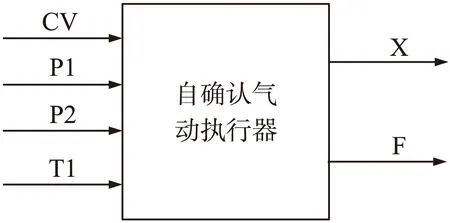
图4 自确认气动执行器模型原理图

当执行器给定的参数无法稳定在规定的范围内,同时不能完成规定的功能,我们视它为发生故障。文献[7]中总结了气动执行器的19种典型故障,具体见表1。

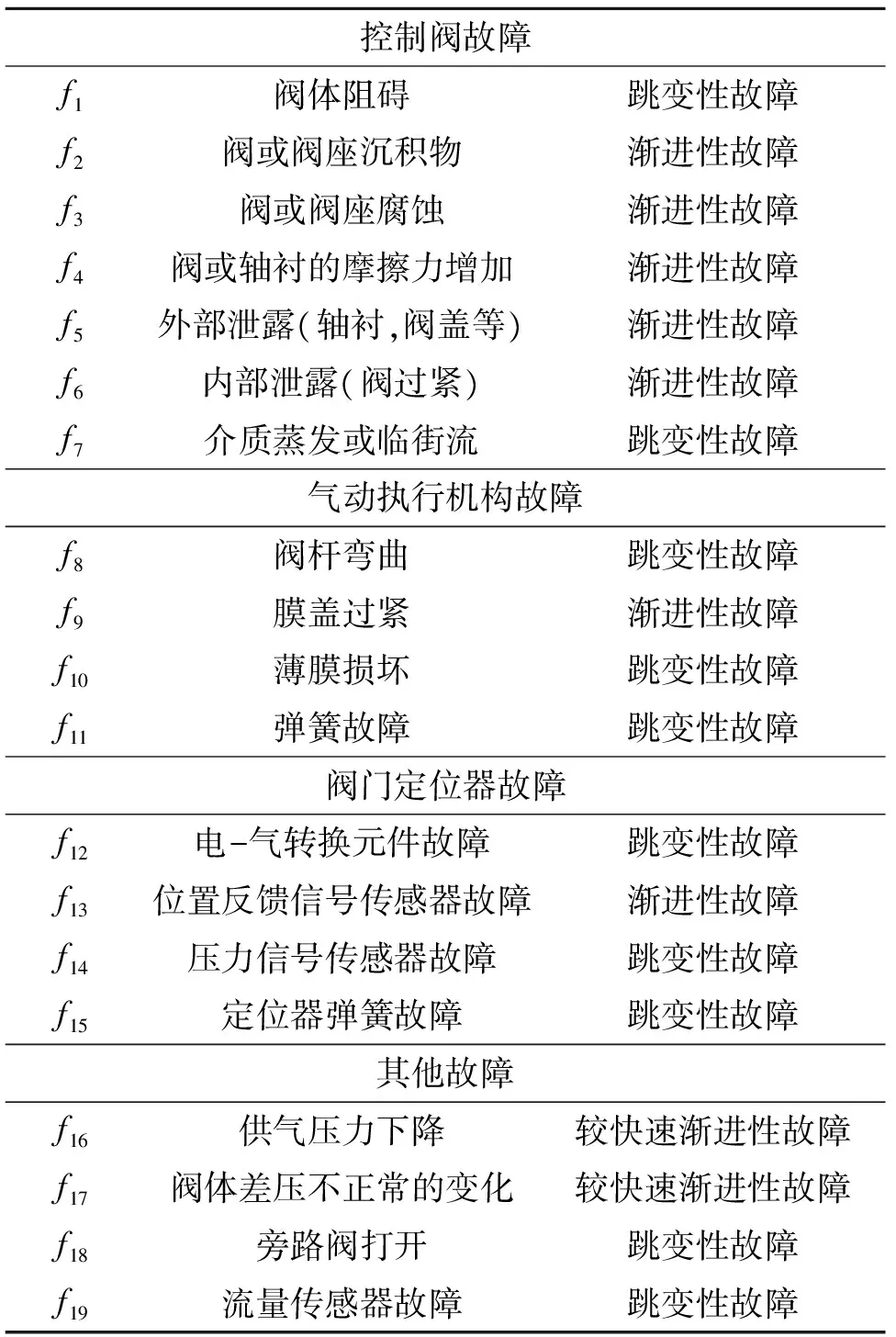
表1 气动执行器的19种典型故障

2 基于MVRVM的建模方法

2.1 MVRVM回归原理

Thayanantha等人在贝叶斯概率框架理论[8]的基础上于2008年提出了模型较为稀疏的MVRVM理论[9-10],目的为实现多变量的同时回归。由图4可知,自确认气动执行器是四输入二输出系统,此方法对于自确认气动执行器的建模问题非常恰当。因为MVRVM回归在小样本下仍具有较好的泛化能力,可保证建模精度,同时模型稀疏,复杂度不高。作为一种核学习方法,它将自确认气动执行器建模中复杂的输入输出关系映射到线性的高维空间中,可解决其非线性问题。

y(n)=Φ[x(n)]·W

(1)

MVRVM算法的基本原理简要分析如下:

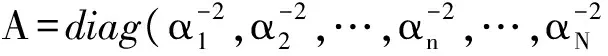
(2)

(3)

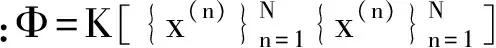
若目标样本集中第m个待重构成分的向量记为τm,wm是对应权值向量,则W的似然分布也可如式(4)所示。

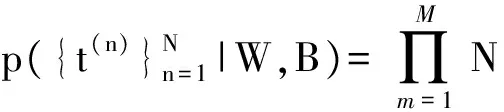
(4)

再者,权值矩阵W的先验分布如式(5)所示,此时W的后验概率则是每一个独立的待重构成分且服从高斯分布的权值向量内积,如式(6)所示,进一步推导如式(7)所示。

(5)

(6)

(7)

(8)

(9)

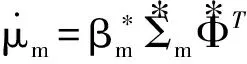
(10)

(11)

(12)

相应地,若最新的测试样本记为是测试样本个数x*∈Rp×q,q是自确认气动执行器输入量个数),则MVRVM模型的多变量输出为y*∈Rp×M,(M是自确认气动执行器输出量个数),误差向量由矩阵σy的对角线元素表征,其数学表达式为:

(13)

(14)

由于在最优超参数计算过程中,随着迭代次数的增加,很多超参数将趋于无穷大,此时相应的大部分权值趋于0,则训练数据集中较多的样本向量将被剔除,较少的相关向量个数被保留,从而实现模型的稀疏化。

2.2 MVRVM回归模型的建立

基于上述MVRVM的理论知识和自确认气动执行器的结构原理、动作的原则,以及自确认气动执行器输入和输出之间的关系,自确认气动执行器的模型可以表示为式(15)。公式中各个量的物理意义见1中的说明。

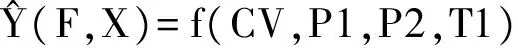
(15)

若执行器产生故障,流体流量信号F或阀杆位置反馈信号X就产生异常现象,上面如式(15)的函数关系就会改变。直观的故障诊断方法是分析残差,即故障执行器的输出和正常的执行机构输出之间的差异。从上面的模型,可以计算残差方程(16)。

(16)

本文选择高斯核函数(K(x,z)=exp(-‖x-z‖2/2σ2)),并设计合适的带宽和最大迭代次数,构造了MVRVM回归模型,其中参数σ直接影响MVRVM回归性能。把执行器的无故障数据作为学习样本来训练设计执行器模型,接着把实际输出和模型的输出进行比较,得到残差r。如果r发生了异常,则认为执行器发生了故障。将残差作为特征向量带入关联向量机即可识别出故障状态。

以无故障数据和故障f1,f2,f15为例,其中数据点取故障发生前后各100点,如图5～图8所示。从图5可以看出,当无故障时,输出残差很小;从图6可以看出,当发生故障1时,r1和r2均有较大值,且r1为负,且其绝对值变化趋势为逐渐减小,r2为正,且其绝对值变化趋势为逐渐减小;从图7可以看出,当发生故障2时,r2发生较大变化,r1基本不变;从图8可以看出,当发生故障15时,r1和r2均有较大值,且r2为负,且其绝对值变化趋势为逐渐增加,r1为正,且其绝对值变化趋势为逐渐增加。即当发生故障时,残差将发生变化,且不同故障的残差改变形式不一样,因此利用残差作为特征,用于自确认气动执行器的故障诊断。

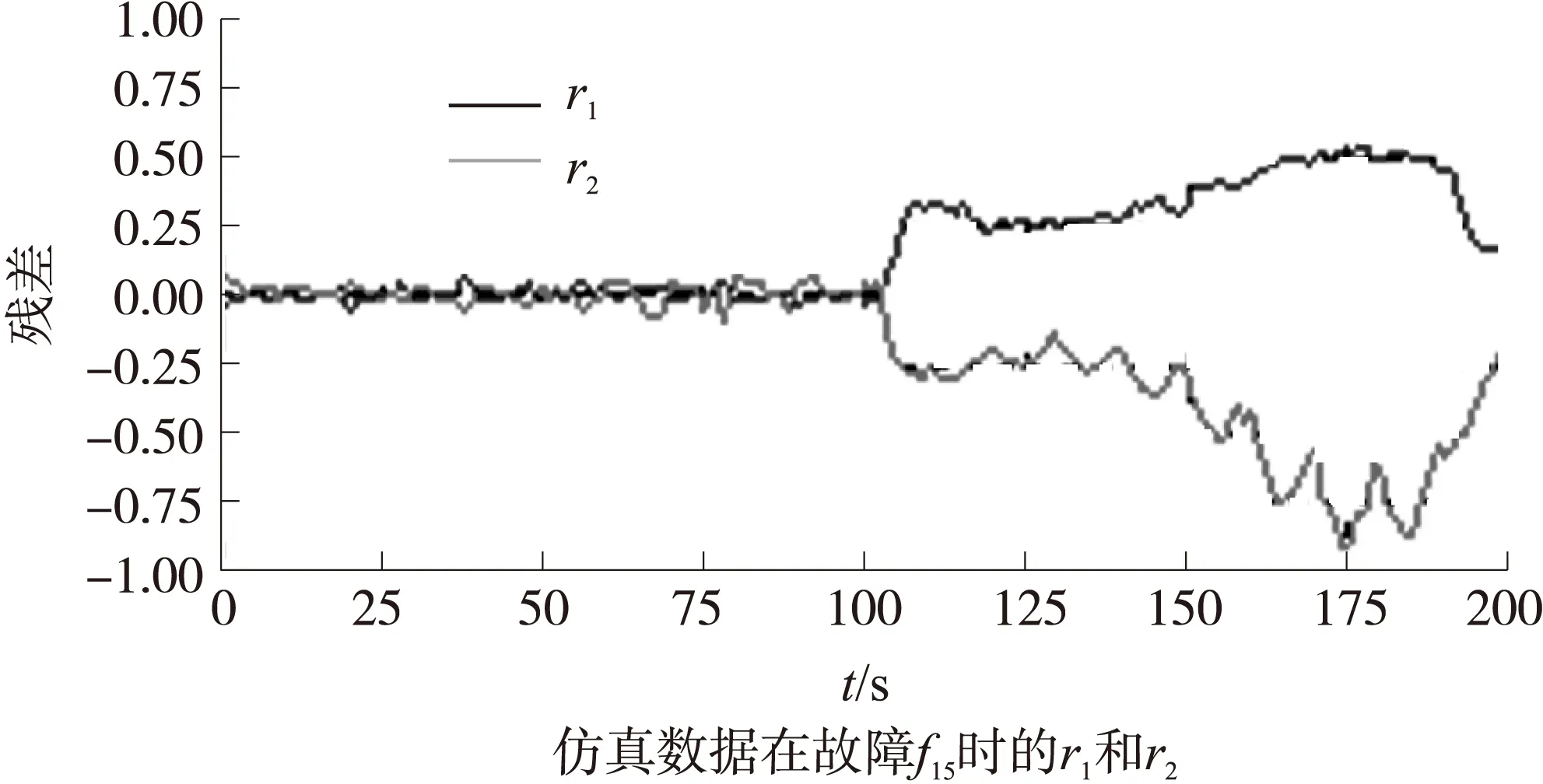
图8 故障15仿真数据输出的残差r1和r2

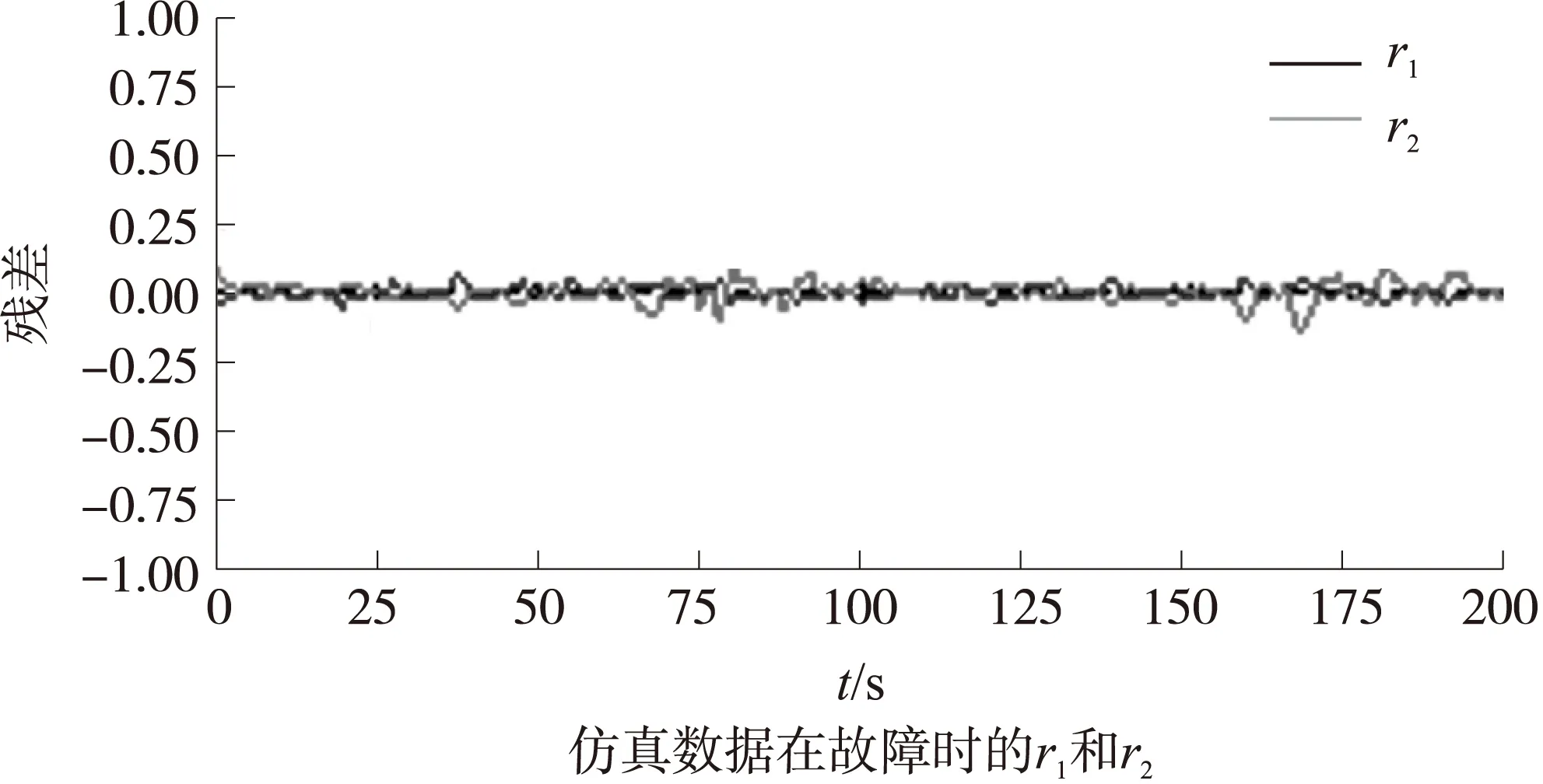
图5 无故障仿真数据输出的残差r1和r2

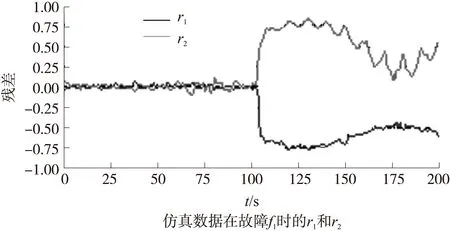
图6 故障1仿真数据输出的残差r1和r2

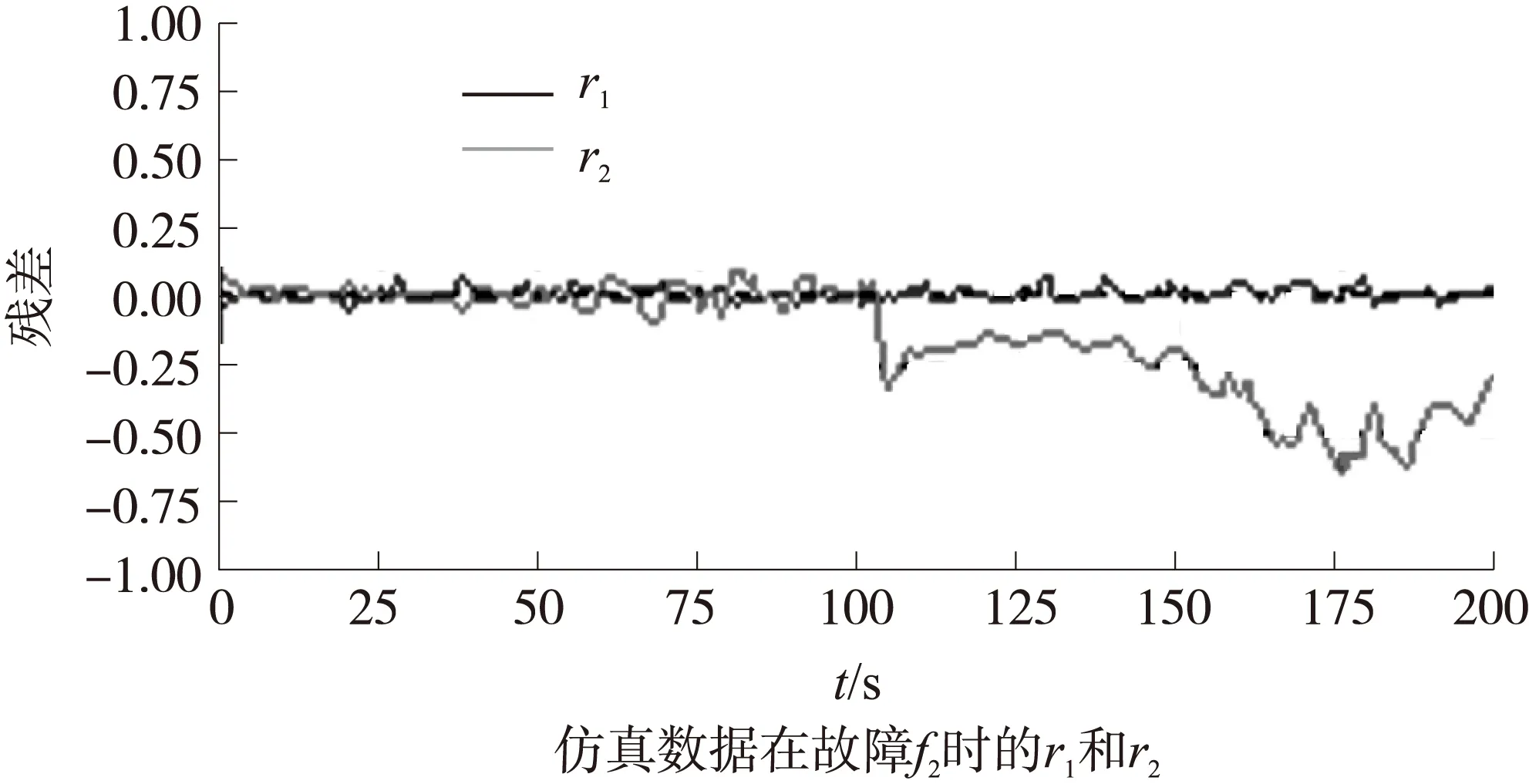
图7 故障2仿真数据输出的残差r1和r2

3 基于RVM二叉树分类的气动执行器的故障诊断

3.1 RVM二分类原理

本文选用RVM二叉树实现自确认气动执行器的故障状态识别。类似于支持向量机,基本的RVM也为二分类器[11-13],对于多种故障可通过一对一(OAO)、一对多(OAA)或二叉树分类方式解决。此外,RVM可直接实现多分类。在二分类问题中,利用分类问题中常用的sigmoid函数σ(y)=1/(1+e-y),则概率函数为:

p(ti=1|ω)=σ(y(xi;w))=1/(1+e-y(xi,w))

多主体梯级水电参与日前市场下游电站自调度投标策略//张粒子,刘方,许通,蒋燕,李秀峰,徐宏//(19):27

(17)

假如所有观测样本间是相互独立的,由伯努利分布,其似然函数可以表述为:

(18)

式中:tn∈{0,1}为目标值。似然函数由下式完成:

(19)

式中:α=[α0,α1,α3,…,αn]T是用来引入控制相关前置权重的超参数。之后,给一个新的测试样本x*,预测相关目标值t*,其预分部为:

p(t*|t)=∫p(t*|ω)p(ω|t)p(α|t)dωdα

(20)

式中:p(ω|t,α)是后验分布,可以用p(α|t)来验证。权重不能通过分析直接获得,因此通过拉普拉斯变换获得。

①对于当前的超参数α,其“最适合”的权重ωMP是通过给定的后验分部得到的,p(ω|t,α)∝p(t|ω)p(ω|α),而后验分布的极值问题相当于下式的最大值:

log{p(t|ω)p(ω|α)}=

(21)

最优权重ωMP、yi=σ{y(xi;ω)}与A=diag(α0,α1,…,αn)共同组成当前值α。这是一个判罚逻辑数似然函数,并且需要达到迭代最大化。ωMP可用所述迭代加权最小二乘算法得到。

②Logistic对数似然函数经过两次微分可以得到如下式(21)的Hessian矩阵:H=WWlog[p(t|ω)p(ω|α)]=(-ΦTBΦ-A)

(22)

式中:B=diag(β1,β2,…,βn)是βi=σ[y(xi;ωMP)]{1-σ[y(xi;ωMP)]}的对角矩阵,Φ是设计矩阵,其中Φnm=K(xn,xm),Φn0=1。然后,该结果取反,反转得到如下式(22)的协方差Σ,对于高斯近似到后验超过权重集中在ωMP:

Σ=-H-1=(ΦTBΦ+A)-1

(23)

(3)利用高斯近似值统计协方差Σ与均值ωMP,用如下更新超参数:

(24)

式中:ωMPi是权重ωMP第i个元素,Σi,i是协方差Σ第i个元素。在优化过程中,有一些αi的值很大,因此,我们设置它的权值,以将αi去除,由此实现稀疏化。优化过程一直持续,直到αi最大变化值低于某个阈值或者达到最大迭代数,然后,我们可以预测分类结果为一个新的值x*。

(25)

RVM分类器的训练步骤如下:

①初始化{αi}。

④重复②和③直到满足收敛条件和得到最大迭代次数。

⑤其中的非零权重即为关联向量。

⑥运用式(25)可以计算得到预测分类结果。

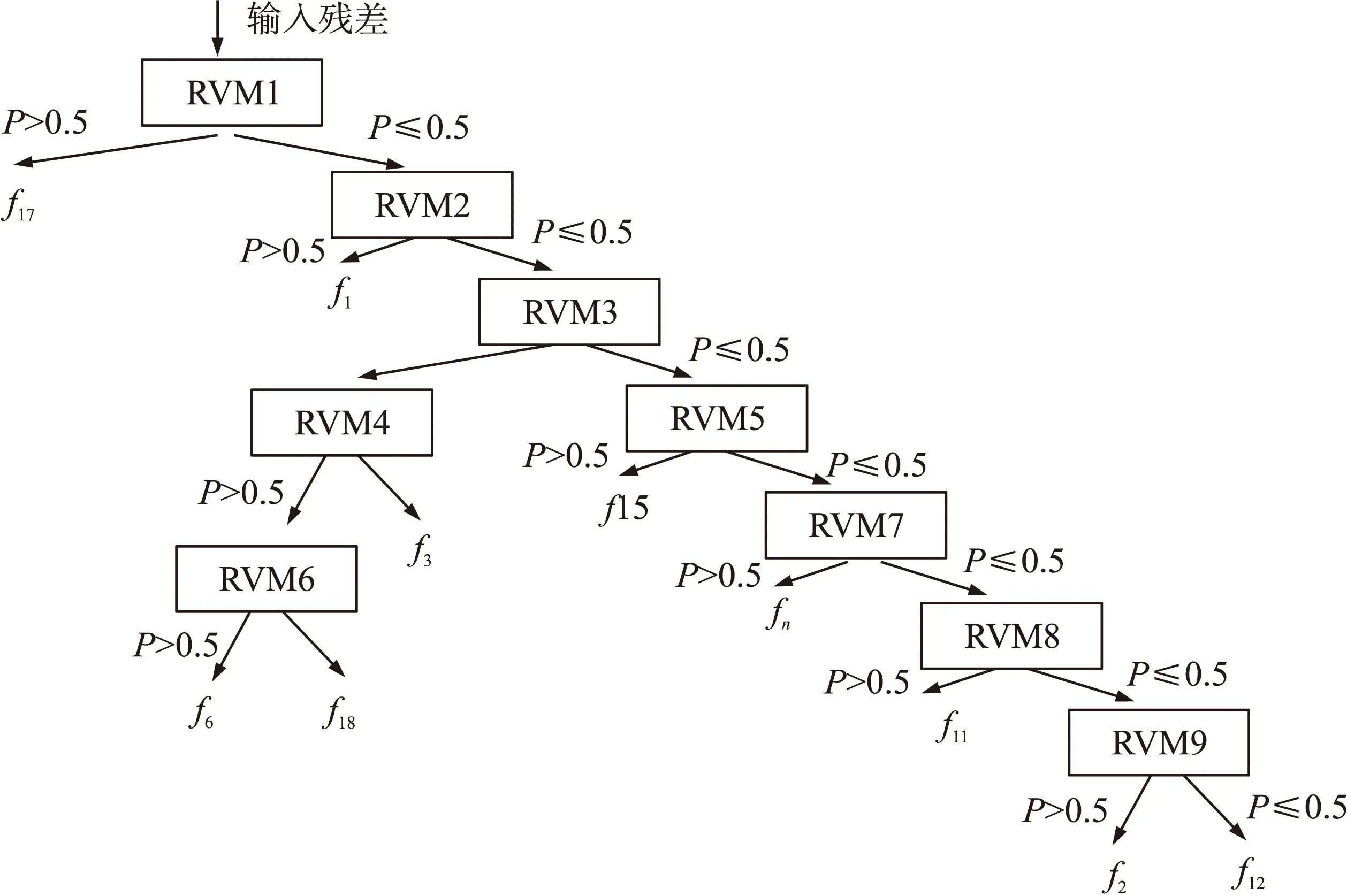
图9 基于RVM的二叉树多分类器拓扑结构

3.2 RVM二叉树多分类器设计

类似支持向量机,基本的关联向量机也是一个二分类器,要实现多分类,可以采用一对一(OAO)方法,一对多(OAA)方法,二叉树分类法,或直接分类[14]。本文的分类器设计采用RVM二叉树分类。用上述MVRVM回归时产生的残差数据作为输入特征向量。利用聚类方法,设计二叉树关联向量多分类机的拓扑结构,如图9所示,本文中只考虑f1、 f2、 f3、 f6、 f11、 f12、 f15、 f17、 f18和fn的状态识别,因此创建9个基于关联向量基的子两分类机(RVM1～RVM9),按照图9的层次结构将这9个子两分类机组合起来,就形成能够将10种状态区分开来的多分类机。每个节点是一个RVM二分类器。

4 应用实例与分析

本文的数据来源为波兰华沙工业大学开发的基于MATLAB-SIMULINK的DABLib执行器模型库,利用此模型库,仿真生成气动执行器故障数据,对所研究方法进行验证。本文首次将关联向量基回归和多分类关联向量基结合起来进行气动执行器故障诊断。具体的诊断步骤如下,首先用多变量关联向量机回归建模,利用无故障情况下的气动执行器的数据作为输入,将模型产生的输出与实际的输出作比较,得到残差,若有发现残差产生异常则说明有故障生成,把提取的这些残差当做特征向量,同时作为多分类关联向量机输入进行训练,便可识别气动执行器的故障。

①使用无故障的数据进行训练建立执行器多向量RVM回归模型g。

②训练过程。首先将训练样本输入基于多变量RVM回归执行机构模型,得到模型预测值,然后通过对比模型预测输出与实际执行器输出生成残差,并它用作RVM二叉树分类器的输入特征向量,最后训练设计RVM多分类器。

③故障识别过程。对于自确认气动执行器的测试数据,首先,利用执行器模型g生成残差,然后,通过将残差带入RVM多分类器进行故障类型的辨识。

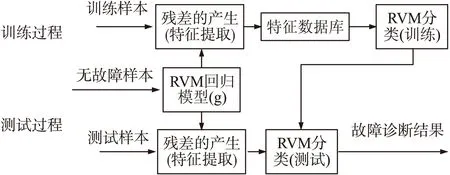
图10 基于RVM的自确认气动执行器故障诊断算法原理图

利用DABLib生成了自确认气动执行器每种故障及正常状态各190组数据,利用190组正常数据建立基于MVRVM回归的气动执行器模型,任意选取每种故障及正常状态各20组数据作为训练样本,输入到建立好的气动执行器模型,产生残差,用于训练RVM多分类机,其余的每种故障及正常状态各170组数据用于对算法的测试。表2给出了详细的测试样本的故障识别结果。具体每一个关联向量机的详细结果如表3所示。

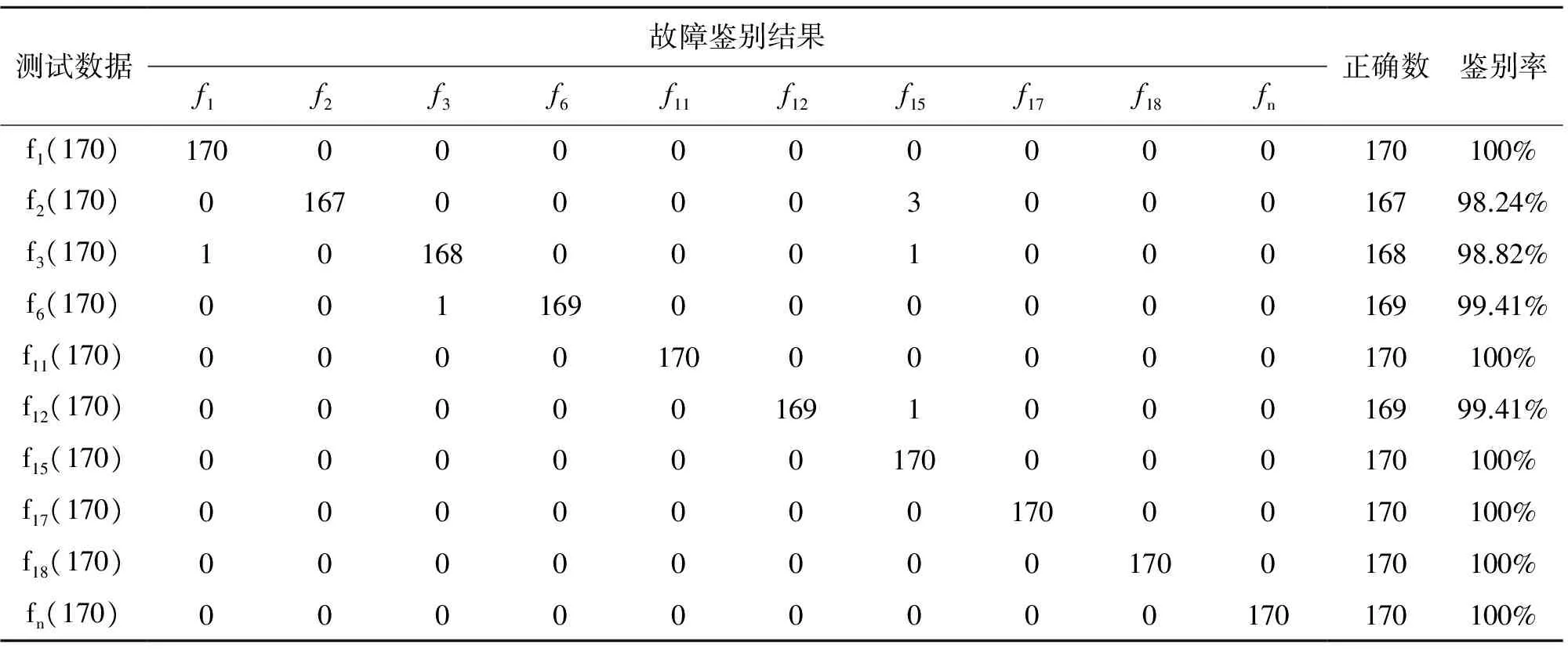
表2 测试样本的故障诊断结果(二叉树分类)

表3 RVM多分类器中的每一个关联向量机的详细结果(二叉树分类)

由表2我们可看出:f1、f11、f15、f17、f18和fn的所有测试样本均被正确识别。3个f2的测试数据被错误识别为f15,这是由于RVM5分类错误导致的;1个f3被错误识别为f1,这是由于RVM2分类错误导致的;1个f3被错误识别为f15,这是由于RVM3分类错误导致的;1个f6被错误认识别为f3,这是由于RVM4分类错误导致的;1个f12被错误识别为f15,这是由于RVM5分类错误导致的。且由表3可见,每个相关向量机的相关向量数量远远低于训练样本数据,即相关向量机具有很强的稀疏性,可以大大提高在线识别的实时性。

为了验证RVM二叉树多分类的优势,我们把RVM二叉树分类方式和RVM一对一分类方式的RVM多分类器进行比较。为保证比较的公平性,同样选择经过MVRVM模型得到的残差特征,选取相同的每种故障及正常状态各20组样本用于训练RVM一对一多分类器,剩余的170组模拟数据进行测试。测试结果如表4所示。

表4 测试样本的故障识别结果(一对一分类)

由表4我们可看出:f1、f6、f15、f18和fn所有测试样本均被正确识别。2个f2的测试数据被错误识别为f15,1个f2的测试数据被错误识别为f3,1个f3被错误认识别为f6,2个f3被错误识别为f15,1个f11被错误识别为f18,2个f12被错误识别为f15,1个f17的测试数据被错误识别为f1。可见对于RVM一对一多分类方法,虽有几处误识别,但所有故障模式的识别率也很高。但是由于采用RVM一对一实现多分类,对于本文的10种状态识别,需要10*(10-1)/2=45个RVM二分类器,而RVM二叉树方法仅需要9个RVM二分类器,因此其训练时间将远远大于RVM二叉树分类器,同时对于在线识别过程来说,一对一分类方法的平均运算量也是二叉树分类方法的5倍,因此在实时性方面,二叉树方法也是远远优于一对一分类方法。

5 结论

本文首次将基于MVRVM回归建模和RVM二叉树分类的故障诊断方法用于自确认气动执行器的故障诊断,利用波兰华沙工业大学开发的DABLib执行器模型库产生气动执行器数据,对所研究方法进行了验证,并对RVM二叉树分类和RVM一对一分类方法进行了比较,结果表明:①所研究方法能够正确建立气动执行器的模型,RVM二叉树分类法能够以较高的正确率识别气动执行器故障状态,且相关向量数远远小于训练样本数,大大提高了解的稀疏性。②二叉树分类和一对一分类方法的故障诊断的识别率和正确数都很高,但RVM一对一分类方法所建立的关联向量机较多,所以对于在线训练和识别,RVM二叉树分类比RVM一对一分类器占用更少的内存和消耗更少的CPU时间。总之,本文所研究方法是解决气动执行器故障诊断的小样本和非线性问题的一种有效方法。

[1] 师黎,费敏锐. 气动执行器故障诊断与容错控制的研究进展[J]. 自动化仪表,2004,25(8):4-9.

[2] 冯志刚,张学娟. 基于LS-SVM和SVM的气动执行器故障诊断方法[J]. 传感技术学报,2013,26(11):1610-1616.

[3] Henry M P,Clarke D W. The Self Validating Sensor:Rationale,Definitions and Examples[J]. Control Engineering Practice,1993,1(4):585-610.

[4] Feng Zhigang,Qiu Meng. Design and Implementation of Self-Validating Pneumatic Actuator Hardware System Based on DSP and MCU[J]. International Journal of Hybrid Information Technology,2014,7(6):101-114.

[5] Karpenko M,Sepehri N,Scuse D. Diagnosis of Process Valve Actuator Faults Using a Multilayer Neural Network[J]. Control Engineering Practice,2003,11(11):1289-1299.

[6] Faisel J,Ron J,Witczak M. A Neuro-Fuzzy Multiple Medel Observer Approach to Robust Fault Diagnosis Based on the DAMADICS Benchmark Problem[J]. Control Engineering Practice,2006,14(6):699-717.

[7] Michal B,Ron P,Michal S. Introduction to the DAMADICS Actuator FDI Benchmark Problem[J]. Control Engineering Practice,2006,14(6):577-596.

[8] 沈强,刘洁瑜,王琪,等. 基于相关向量机的MEMS陀螺仪随机漂移补偿[J]. 传感技术学报,2014,27(5):596-599.

[9] Thayananthan A,Navaratnam R,Stenger B,et al. Multivariate Relevance Vector Machines for Tracking[C]//Proceedings of the 2006 European Conference on Computer Vision,2006,3953:124-138.

[10] Thayananthan A,Navaratnam R,Stenger B,et al. Pose Estimation and Tracking Using Multivariate Regression[J]. Pattern Recognition Letters,2008,29(9):1302-1310.

[11] Dong Chao,Zhao Huijie, ,et al. Hyperspectral Image Classification and Application Based on Relevance Vector Machine[J]. Journal of Remote Sensing,2010,14(6):1273-1278.

[12] Tipping M E. Sparse Bayesian Learning and the Relevance Vector Machine[J]. Journal of Machine Learning Research,2001:211-244.

[13] 董超,田联房,赵慧洁. 遗传关联向量机高光谱影像分类[J]. 上海交通大学学报,2011,45(10):1516-1520.

[14] Yu Jintao,Ding Mingli,Meng Fangang,et al. Acoustic Emission Source Identification Based on Harmonic Wavelet Packet and Support Vector Machine[J]. Journal of Southeast University:English Edition,2011,27(3):300-304.

冯志刚(1980-)男,副教授,2009年获哈尔滨工业大学测试计量技术及仪器专业博士学位,现为沈阳航空航天大学自动化学院副教授,硕士生导师,主要从事自确认执行器、自确认传感器、系统故障诊断等方面的研究,fzg1023@yeah.net。

Self-Validating Pneumatic Actuator Fault Diagnosis Based on MVRVMRegression and RVM Binary Tree Classification*

FENGZhigang*,WANGRu,TIANFeng

(Department of Automation,Shenyang Aerospace University,Shenyang 110136,China)

In order to solve the fault diagnosis problem of self-validating pneumatic actuators,a fault diagnosis approach based on multi-variable relevance vector machine(MVRVM)and relevance vector machine(RVM)binary tree classification is proposed. The MVRVM regression is used to establish the normal model of the pneumatic actuator. The residuals generated by comparing the output of the model and the actual actuator are used as the nonlinear features of the pneumatic actuator. Then the RVM multi-classifier based on binary tree is established and trained by the residuals,which is used to identify the condition and fault pattern of the actuator. The proposed approach is verified using fault data generated by DABLib model and compared with RVM one-against-one multi-classification method. The results indicate that the proposed approach is a valid method to resolve the small sample and nonlinear problem in pneumatic actuator fault diagnosis.

self-validating(SEVA)pneumatic actuator;relevance vector machine(RVM);multi-variable relevance vector machine(MVRVM);relevance vector machine(RVM)binary tree classifier;relevance vector machine(RVM)one-against-one classifier;fault diagnosis

项目来源:国家自然科学基金青年基金项目(61104023)

2015-01-22 修改日期:2015-03-01

C:7230;0170L

10.3969/j.issn.1004-1699.2015.06.012

TP214;TP18

A

1004-1699(2015)06-0842-08