用质控图法和稳健统计法评估热裂解-原子吸收光谱法测量固体样品汞含量的不确定度

周瑞 狄一安 于跃 杨勇杰 李玉武

（国家环境分析测试中心，北京100029）

用质控图法和稳健统计法评估热裂解-原子吸收光谱法测量固体样品汞含量的不确定度

周瑞 狄一安 于跃 杨勇杰 李玉武＊

（国家环境分析测试中心，北京100029）

基于实验室长期积累的质控数据评估测量不确定度的top-down方法具有广泛应用前景，质控图法和稳健统计法是其中常见方法。质控图法要求测量数据中不含离群值，对测量数据时间顺序有明确要求。稳健统计法是指不用识别、剔除离群值，直接应用全部测量数据，将离群值对统计分析结果影响降低到最小的统计分析方法。基于质控图法、稳健统计和实验室长期积累的质控数据对固体样品汞含量热裂解-原子吸收光谱分析方法的测量不确定度进行了评估，对两种方法计算结果、实验室评估的测量不确定度和标准样品标称值的不确定度进行了比较。计算结果表明，两种方法结果基本吻合，基于实验室质控数据期间精密度评估的不确定度明显小于标准样品标称值，结果合理。

汞的测定；热解法；测量不确定度评估；质控图法；稳健统计-迭代法

0 前言

目前各种标准或指南中测量不确定度的评估方法大致可分为“bottom-up”和“top-down”两类［1］。“bottom-up”法注重细节，分析、计算分析步骤中每一操作环节所涉及的不确定度分量，计算合成标准不确定度，然后乘以包含因子得到扩展不确定度。“topdown”法利用从方法确认、实验室内质控和/或实验室间协作定值、能力验证等数据，注重从整体上、通过数月、数年等一段期间反映样品检测全过程的精密度数据直接评估测量不确定度。如精密度法［2］、质控图法［3］、线性校准法［4］和经验模型法［5－6］等。近年来国内文献中已出现不少用“top-down”技术来评估测量不确定度研究论文和研究背景介绍［7－12］。这些研究工作将测量不确定度与分析方法的质量参数联系起来，是“top-down”方法的成功应用。

固定污染源废气中汞的监测日益受到环境保护管理部门重视。2015年1月1日起开始将火电厂大气污染物汞及其化合物排放浓度纳入限值管理［13］，并在全国范围各大发电集团下属企业开展了监测试点。用于燃煤电厂废气测汞的活性碳法是美国EPA推荐的监测方法，国内环保部也已经将此方法列入标准制定计划，征求意见稿即将上网公开征求意见。与此方法配套的固体样品热裂解-塞曼效应扣背景原子吸收光谱法具有准确度高、精密度好、分析速度快等优点，是类似活性炭等固体样品汞含量测定的首选方法，在环境样品汞检测分析中已有应用［14］，但相关测量不确定度未见报道。利用基于“top-down”技术理念的质控图法、稳健统计-迭代法和实验室长期积累的质控数据对固体样品汞含量热裂解-原子吸收光谱分析方法的测量不确定度进行了评估，对两种方法评估结果、实验室测量不确定度和标准样品标称值的不确定度进行了比较，为全面评估固定污染源废气汞监测结果测量不确定度奠定了基础。

1 不确定度评估方法

1.1 质控图法［1，3］

在实际测量中，消除或修正系统误差之后，每次测量结果仍会出现一些无规律的随机性变化。通过A＊统计判断，确认数据的波动符合偶然误差正态性、独立性特点。在偏倚受控的期间精密度测量条件下，此时将同一浓度质控样品系列测量数据计算结果期间精密度sR′乘以2，即可视为实验室获得的扩展不确定度。实验室给出的sR′应大于sr，小于sR。具体计算步骤如下：

非离群测量结果xi按升序排列后，其标准化值wi按式（1）计算：

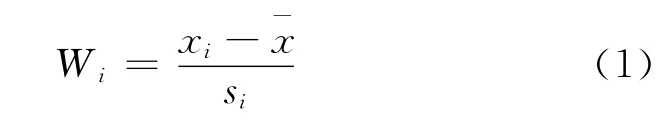
根据相关表格提供的数据，可将wi值换算成正态概率值pi。更方便的方法是利用微软Excel的函数公式NORMDIST（x，mean，std dev，cummulative）语句求出。例如，wi＝－0.64，NORMDIST（－0.64，0，1，TRUE）＝0.261 086，与查表值0.261 1完全一致。统计量A值和A＊值按公式（2）和（3）计算：

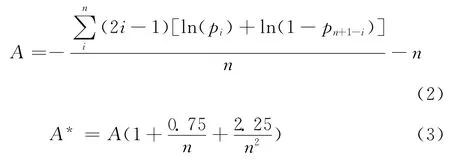
式中：A＊—正态统计量A的修正值。按s式计算时表示为A＊（s），按 MR式计算时表示为A＊（MR）；n—测量次数。

根据A＊（s）和A＊（MR）数值，有如下判定：

（a）A＊（s）＜1.0和A＊（MR）＜1.0，接受数据正态性和独立性的假定；

（b）A＊（s）＞1.0和A＊（MR）＞1.0，表明测量系统失控；

（c）A＊（s）＜1.0和A＊（MR）＞1.0，表明系列结果呈非独立性。

质控图法具有统计学的严格性，因此要求必须有充分的重复次数。

1.2 稳健统计-迭代法

稳健统计-迭代法是近年来ISO标准推荐的稳健统计方法，其应用早在20世纪80年代国外分析化学文献中已有报道，它不需要对离群值进行人为干预。其原理是对按顺序排列，位于数据排列两端远离中位值的可疑值或离群值均以较小权重予以保留，与中位值接近的值则以较大权重参与计算，充分利用了全部测量数据的信息。分析化学领域中，有些离群值很明显，容易删去，但有时判断离群值的分界线并不明显，不同的判别方法结论可能不同。在这种情况下，稳健统计方法尽量减小了离群值对平均值和标准偏差的影响，给出这两个统计量的估计值。稳健统计-迭代法的特点是它不需要假设数据是标准正态分布。在正态分布基础上，单峰分布，基本对称，存在离群值，即使有严重拖尾（heavy tails）现象时，它也能给出较合理的结果。

稳健统计-迭代法具体计算步骤如下：

测量结果xi按升序排列后，计算平均值和标准偏差s。以此数据为基础计算式（4）中的参数（方法1）。

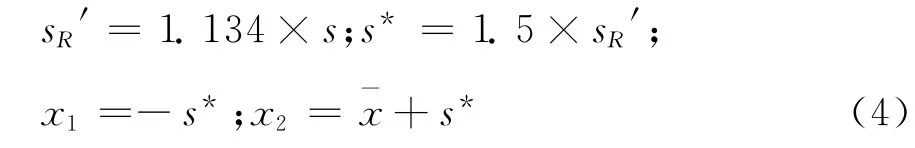
用x1和x2分别取代升序排列数据两端比x1小和比x2大的数据，重新计算新数列平均值和标准偏差s，重新计算x1和x2，分别取代两端数据，直至sR′无明显变化。最终结果按式（5）校正（n为数据个数）。

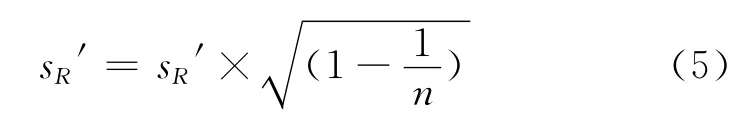
x1和x2初始值也可以按下列方式得到（方法2［1516］）：测量结果xi按升序排列后，取数列的中位值。用排序后的测量数据与中位值相减，求出此差值的绝对值数列的中位值作为标准偏差的估计值s0。以此数据为基础计算式（6）中的参数。

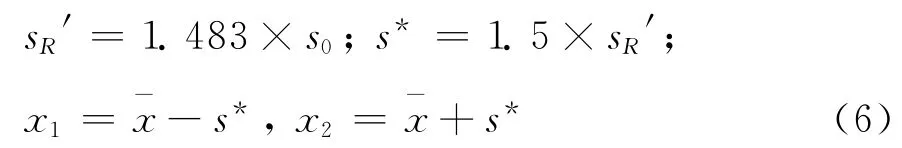
此时将同一浓度质控样品系列测量数据计算结果期间精密度sR′乘以2，即可视为实验室获得的扩展不确定度。质控图法和稳健统计-迭代法计算均在Excel软件上完成。

2 实验部分

2.1 分析步骤

测量步骤采用美国EPA标准。将固体样品称重后，放入样品舟内，先通过800℃以上的高温热解装置进行样品中汞的原子化、汞原子对254nm共振辐射的吸收、塞曼背景校正技术处理后经过原子吸收汞分析仪在线实时检测，积分得出样品峰面积，经工作曲线计算得出样品汞含量（ng）。称取不同质量土壤（或沉积物）标准样品（GSS-4土壤标样，汞含量为590 ng/g），换算成汞质量为横坐标，峰面积为纵坐标进行线性回归得到工作曲线（表1）。其斜率用于实际样品汞含量测定。工作曲线相关系数应大于0.999。

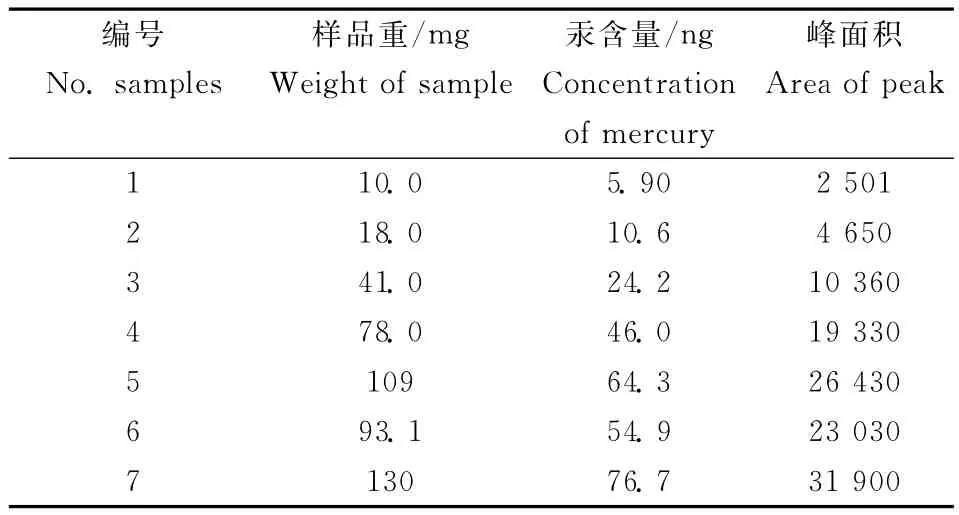
表1 工作曲线原始数据示例Table 1 Example of calibration data set

2.2 数据来源

分别对汞含量为（61±6）ng/g（GSS-7土壤标样）和（280±30）ng/g（GSD-10沉积物标样）两个标样作为质控样在日常检测工作中穿插在实际样品中，按同样操作程序进行测定，时间跨度为2a，测定数据见表2。经检验，表2汇集的测定结果不存在离群值。

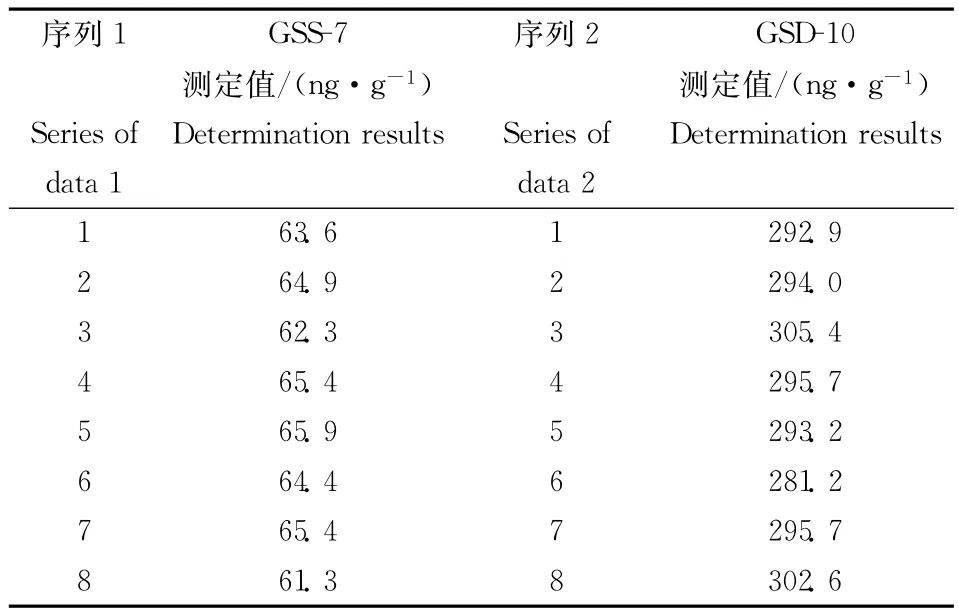
表2 日常检测汞质控样品的系列测量结果Table 2 Measurement data sets of quality control sample collected in routine mercury analysis

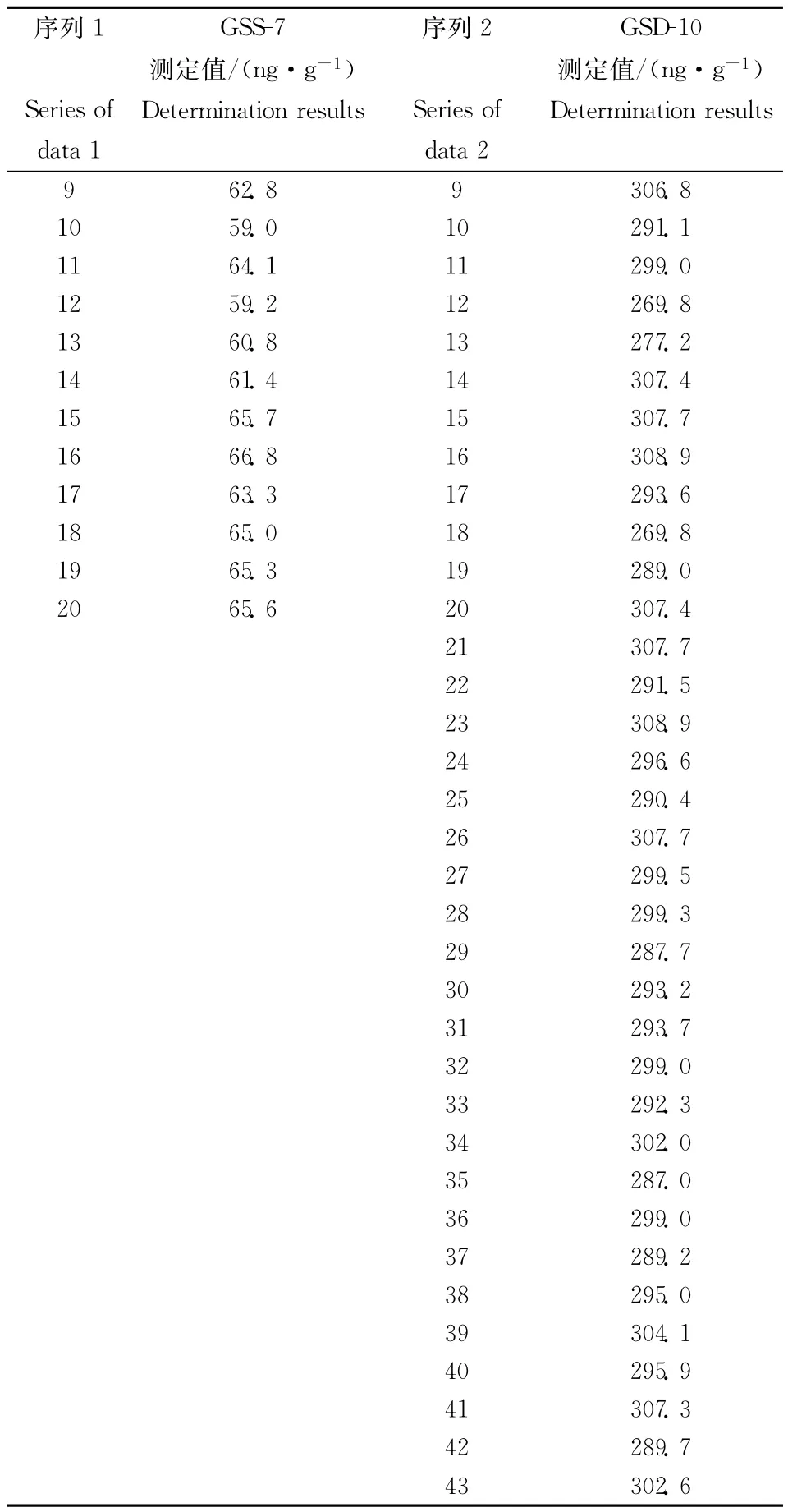
续表2

3 结果与讨论

表3-1和3-2显示了GSS-7和GSD-10两个质控样实验室测量不确定度质控图法计算过程及结果。表中数据按样品测量时间顺序排列，分别列出了根据标准偏差s和移动极差MR计算得出统计量A＊和期间精密度。

从表3-1和3-2两个质控样计算结果可以看出：A＊（s）＝0.658，0.807；A＊（MR）＝0.583，0.806，均小于1.0，因此接受数据正态性和独立性的假定。GSS-7和GSD-10质控样测量不确定度质控图法期间精密度计算结果分别为2.0和9.5。质控图法中正态性和独立性判据可用于判断质控数据的有效性，只有质控数据的正态性和独立性要求同时得到满足，期间精密度结果才可以用于不确定度评估。通过控制图发现移动极差的变化，确保其数据排列呈随机状态，可以及时发现测量体系是否存在系统误差。

稳健统计-迭代法用于能力验证数据处理已得到国际标准认可和推荐［14］，已受到国内检测能力验证专业机构关注［15－16］。用稳健统计方法得到的能力验证数据精密度可以作为实验室间标准偏差的估计值用于检测能力合格性判断。同理，用稳健统计方法处理实验室内部长期积累的质控数据得到期间精密度同样可以用于实验室内部同类样品、相同检测项目测量不确定度评估［12］。

利用稳健统计-迭代法对上述两个系列测量数据也进行了处理，得到实验室内部两个汞质控样期间精密度及测量不确定度。计算过程见表4-1和表4-2。表4两个系列质控数据经过5轮迭代计算期间精密度即可收敛。质控图和稳健统计法两种方法结果比较见表5。从表5可看出，两种方法计算结果没有明显差别。相对标准不确定度约为3.0%～3.6%。稳健统计法优点是它不需要对离群值进行识别和剔除，可将离群值对统计结果平均值和标准偏差的影响降低到最小。同时对测量数据顺序没有要求。

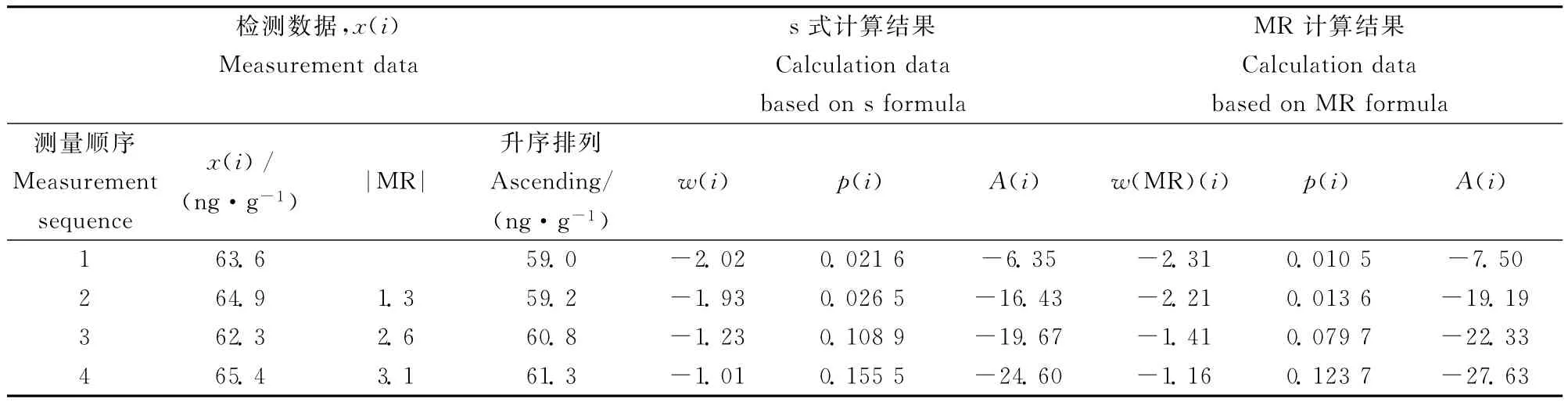
表3 -1 GSS-7质控样测量不确定度质控图法计算过程及结果Table 3-1 Example for evaluation of measurement uncertainty by quality control charting method（GSS-7）

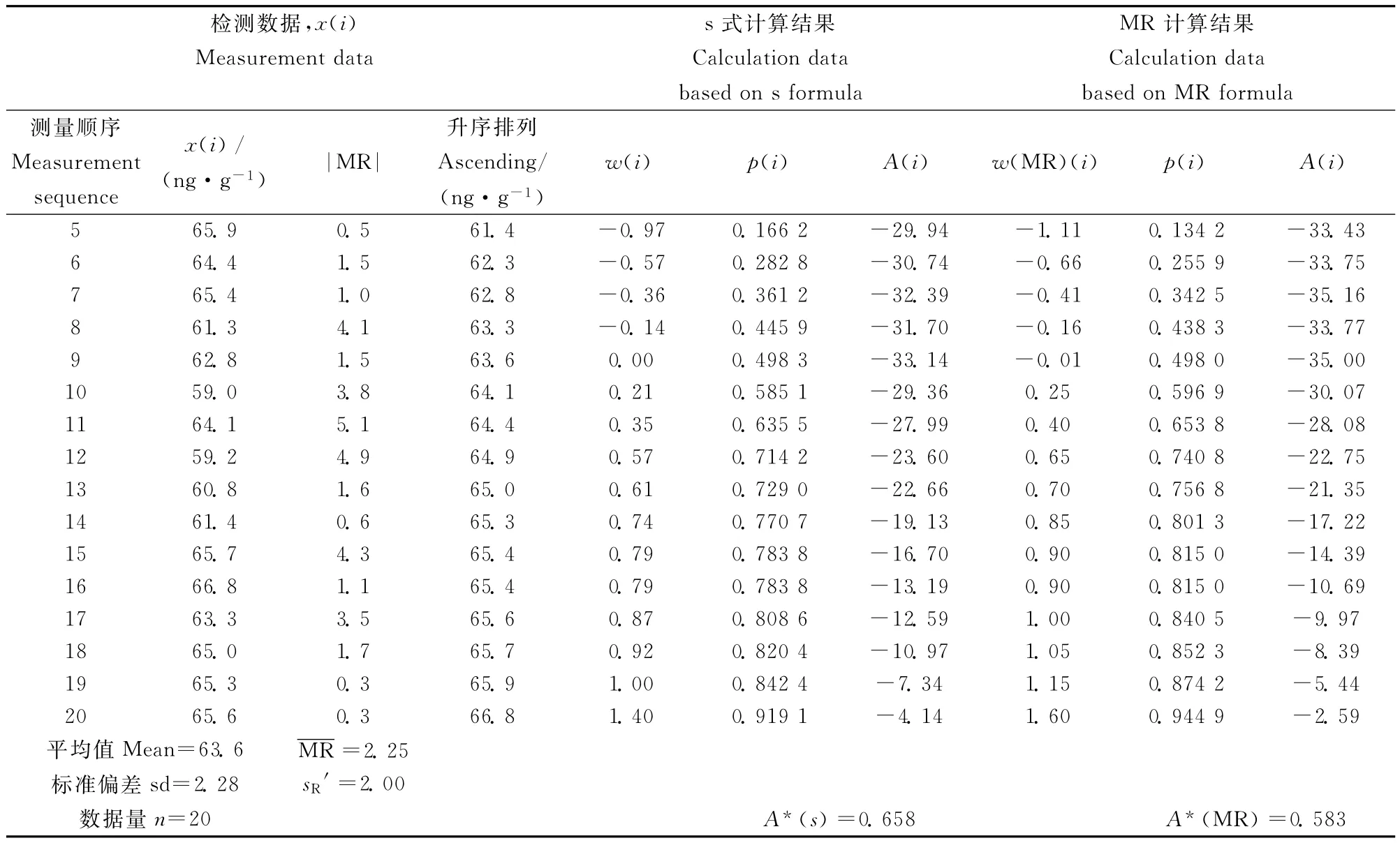
续表3-1

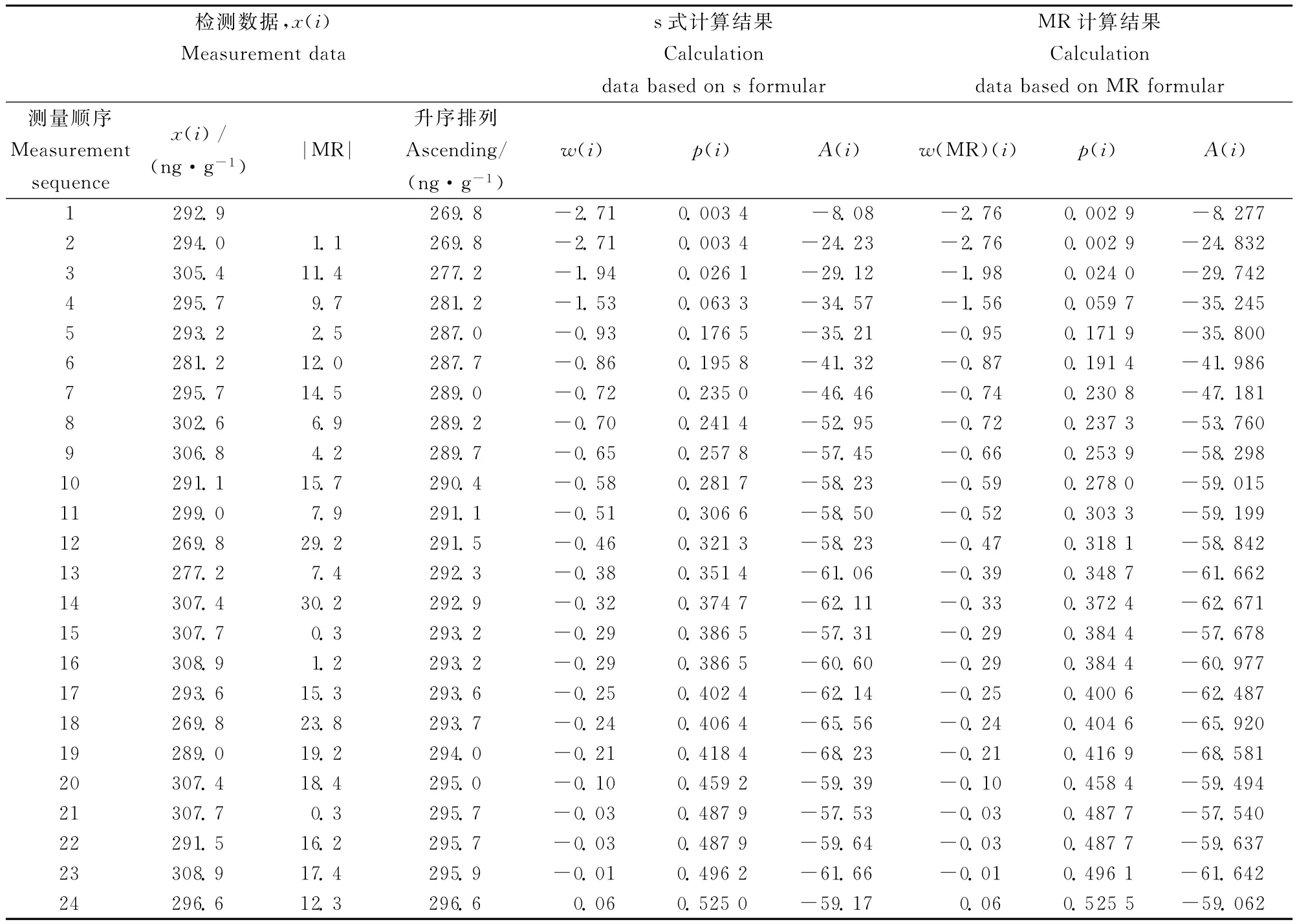
表3 -2 GSD-10质控样测量不确定度质控图法计算过程及结果Table 3-2 Example for evaluation of measurement uncertainty by quality control charting method（GSD-10）

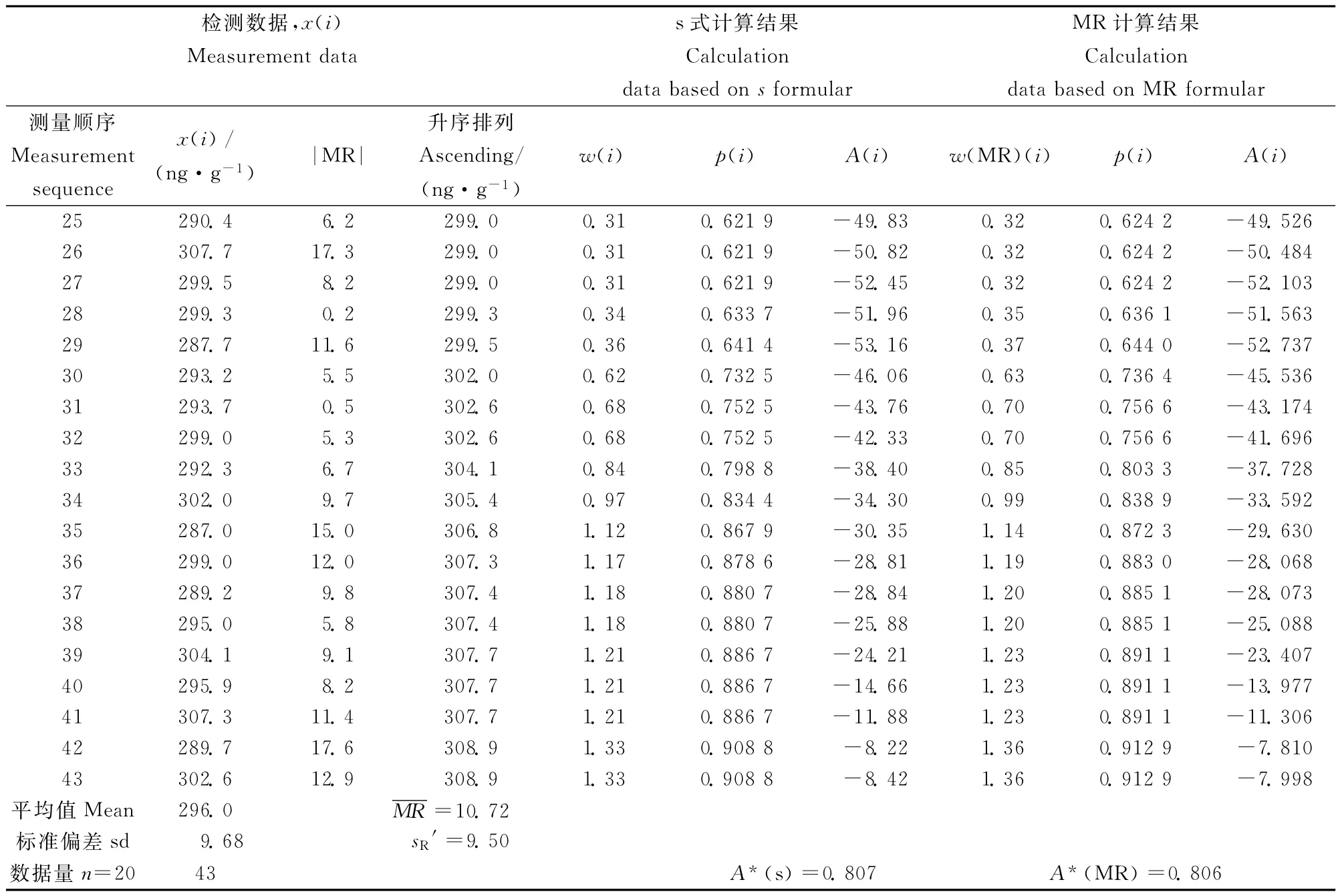
续表3-2

与标样原标称值（61±6）ng/g（GSS-7）和（280±30）ng/g（GSD-10）相比较，实验室内测量值平均值（63.7和297）略大于标准值，经t值检验，两者没有显著统计差别。两系列质控数据期间精密度均小于根据标准样品标准值不确定度计算的实验室间再现性标准偏差，结果合理。由于原标样定值采用的测试方法中涉及消解前处理，而固体样品直接进样分析减少了前处理过程的不确定度性因素，这也可能是固体直接进样测汞方法结果平均值偏高和期间精密度小的原因之一。

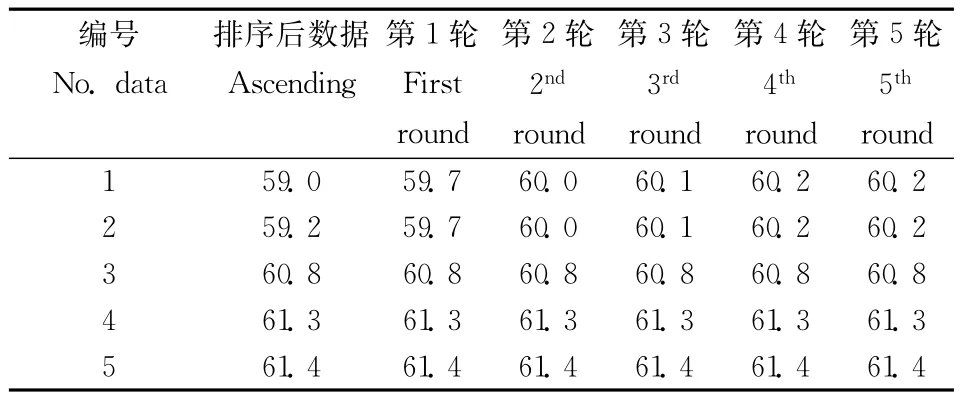
表4-1 GSS-7质控样测量不确定度稳健统计-迭代法计算过程及结果Table 4-1 Example for evaluation of measurement uncertainty by robust statistics-iteration method（GSS-7）/（ng·g－1）

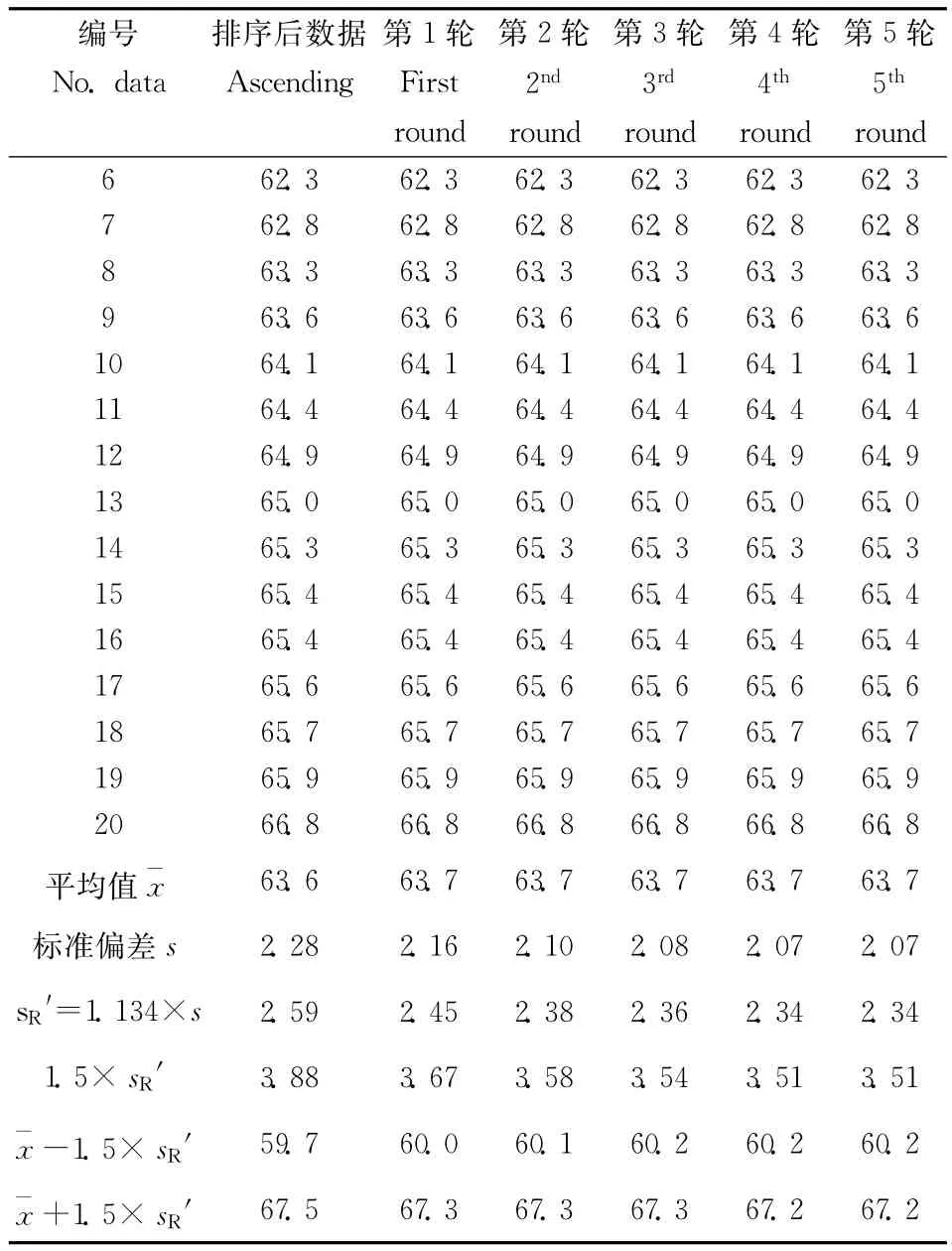
续表4-1/（ng·g－1）

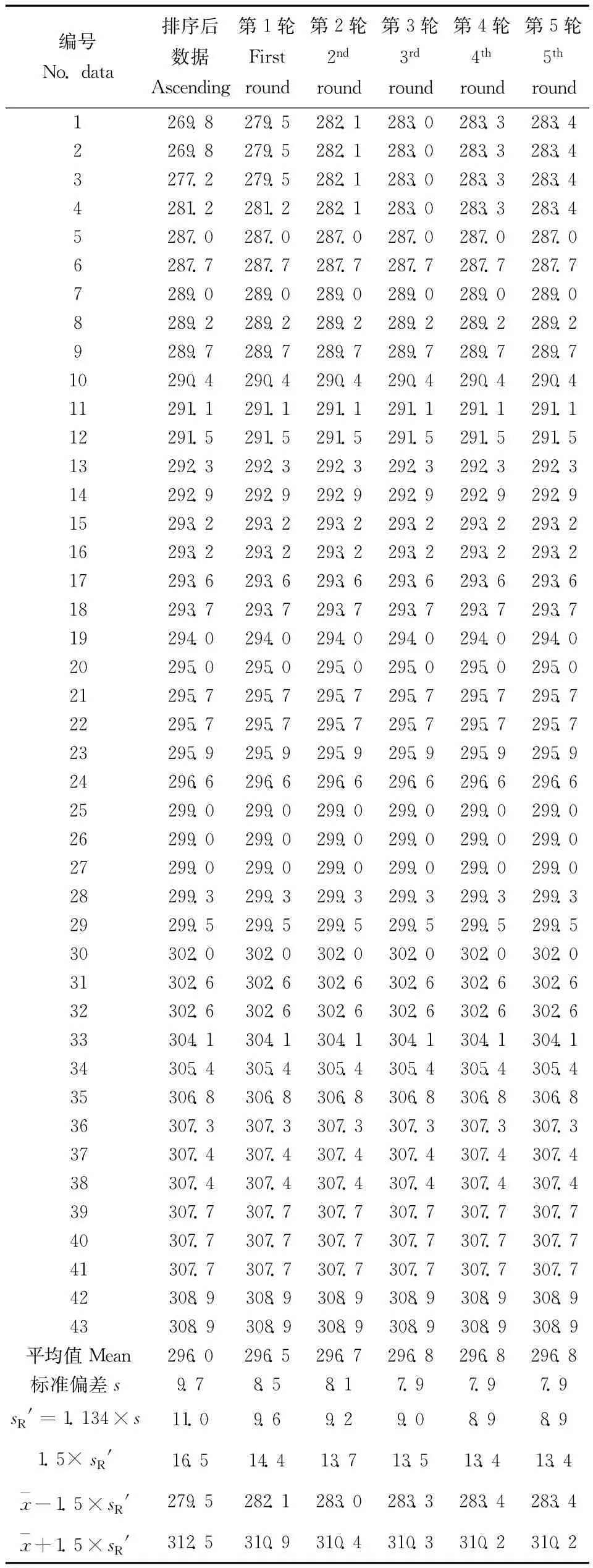
表4 -2 GSD-10质控样测量不确定度稳健统计-迭代法计算过程及结果Table 4-2 Example for evaluation of measurement uncertainty by robust statistics-iteration method（GSD-10）/（ng·g－1）

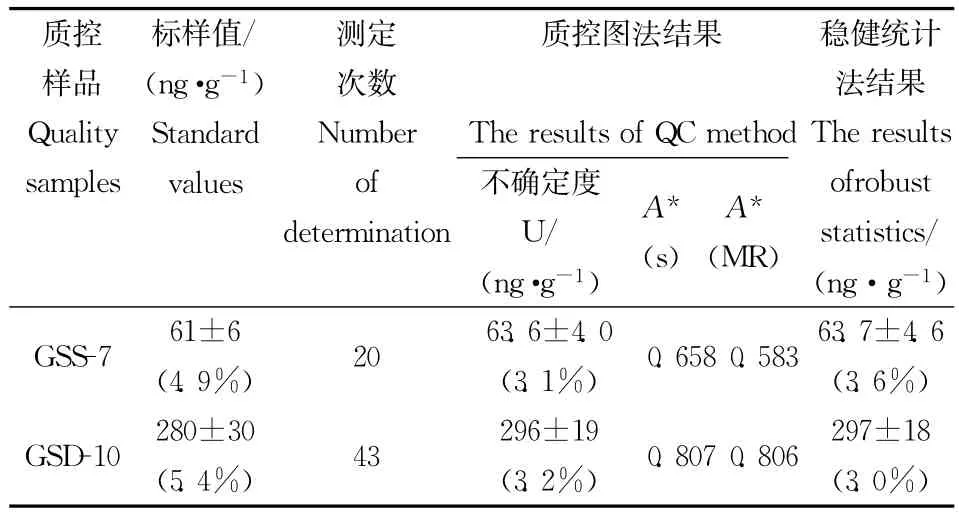
表5 质控图法和稳健统计法结果比较Table 5 Comparisonof result from quality control charting and robust statistics

将两系列质控数据分别除以其平均值，得到回收率。归一化后的数据作为一个系列数据分别用质控图法和稳健统计法处理，回收率平均值分别为99.7%和100.0%，相对期间精密度均为3.2%。这意味着，在这两个含量范围内的样品测定结果乘以0.032，可作为样品测量结果标准不确定度的估计值。

目前经CMA（计量认证）和CNAS（实验室认可）的化学实验室大多都运行有一套成熟的质量保证和质量控制体系。实验室在确保它的测量系统受控，对检测方法操作熟练的前提下，通过长期、大量的质控活动积累了完整的原始数据。这为成功应用“Top-down”方法，如质控图法和稳健统计法提供了可能。这也符合CNAS-GL06的要求，强调不确定度的评定应与实验室内部的质量控制紧密结合起来，这样才能确保其提供有效的量值溯源质量数据来进行不确定度评定。

“Top-down”评定方法大幅度减少了实验室有关人员进行不确定度评估的工作量，并且易于在日常检测工作中得到实施，便于在化学检测领域进行推广。由于化学检测的特殊性，使用这种方法评定测量不确定度快速、简便、可操作性强。所以在日常化学分析检测领域具有一定的可行性和推广性。

4 结论

利用质控图法和稳健统计法对两个系列固体汞标样测量数据评估了固体样品-热裂解-原子吸收光谱分析法测量不确定度。两种方法计算结果基本吻合，相对标准不确定度约为3.0%～3.2%。与标样标称值相比，实验室内期间精密度均小于标样定值的标准不确定度，结果合理。

［1］中国实验室国家认可委员会 .环境检测领域基于质控数据评定测量不确定度指南［S］.北京：中国标准出版社，2013.

［2］中国国家标准化管理委员会.GB/Z 22553—2010利用重复性、再现性和正确度的估计值评估测量不确定度的指南［S］.北京：中国标准出版社，2010.

［3］中国国家标准化管理委员会.GB/T 27407—2010实验室质量控制-利用统计质量保证和控制图技术评价分析测量系统的性能［S］.北京：中国标准出版社，2010.

［4］中国国家标准化管理委员会.GB/T 22554—2010基于标准样品的线性校准［S］.北京：中国标准出版社，2010.

［5］中国国家标准化管理委员会.GB/T 27411—2012检测实验室中常用不确定度评定方法与表示［S］.北京：中国标准出版社，2013.

［6］李玉武，狄一安，孙海容，等 .用经验模型评估环境样品测量不确定度［J］.中国无机分析化学（Chinese Journal of Inorganic Analytical Chemistry），2012，2（1）：1-8.

［7］熊英，郭巨权 .利用重复性和再现性的估计值评估测量不确定度［J］.岩矿测试（Rock and Mineral Analysis），2012，31（2）：350-354.

［8］李宣，慕俊泽，张斌，等.塑料中镉的测量不确定度评定［J］.分析试验室（Chinese Journal of Analysis Laboratory），2007，26（2）：71-74.

［9］罗惠明，任春华，梁希杨，等 .应用实验室能力验证结果评定蒸馏酒中甲醇浓度的不确定度［J］.检验检疫科学（Inspection and Quarantine Science），2007，17（Z1）：8-10.

［10］尹兰风 .复现性限与不确定度评定［J］.中国计量（China Metrology），2002（3）：44-45.

［11］孙海容，杨元华，曹实，等.采用统计控制图法评定检测结果测量不确定度［J］.现代测量与实验室管理（Advanced Measurement and Laboratory Management），2012，20（3）：14-16，60.

［12］狄一安，孙海容，孙培琴，等 .用质控图和稳健统计-迭代法评估环境检测实验室测量不确定度［J］.岩矿测试（Rock and Mineral Analysis），2014，33（1）：55-64.

［13］中国国家标准化管理委员会.GB 13223—2011火电厂大气污染物排放标准［S］.北京：中国标准出版社，2011.

［14］王翠萍，闫海鱼，刘鸿雁，等.使用Lumex测汞仪快速测定固体样品中总汞的方法［J］.地球与环境（Earth and Environment），2010，38（3）：378-382.

［15］佟艳春.拉伸试验能力验证结果的稳健统计指定值及其不确定度［J］.理化检验：物理分册（Physical Testing and Chemical Analysis Part A：Physical Testing），2010，46（2）：70-83.

［16］邢小茹，马小爽，田文，等 .实验室间比对能力验证中的两种稳健统计技术探讨［J］.中国环境监测（Environmental Monitoring in China），2011，27（4）：4-8.

Evaluation of Measurement Uncertainty of Mercury in Solid Samples by Pyrolysis Atomic Absorption Spectrophotometry Using Quality Control Charting and Robust Statistics

ZHOU Rui，DI Yian，YU Yue，YANG Yongjie，LI Yuwu＊
（National Research Center for Environmental Analysis and Measurements，Beijing100029，China）

There are broad application prospects for evaluation of measurement uncertainty in environmental test laboratory by top-down method based on quality control data accumulated in long-term routine analysis.Quality control charting method and robust statistics are two top-down methods.The quality control charting method needs no outliers and clearly requires time sequence in measured data.Robust statistics is a type of statistical analysis method where it is unnecessary to identify and delete outliers but it can also reduce the effect of outliers on the final results based on all measurement data.In this paper，quality control charting method and robust statistics（iteration method）are used to evaluate measurement uncertainty of mercury in solid samples by pyrolysis atomic absorption spectrophotometry，after calculating intermediate precision（sR’）of two quality data sets collected during last two years.The analysis results of the two methods，the measurement uncertainty evaluated in laboratory and that recommended by the standard reference materials manufacture are compared.The results show that themeasurement uncertainty evaluated by two methods is generally in line with each other for solid samples.The values of sR’from laboratory data are evidently smaller than that recommended by the manufacture，which is reasonable according to statistics principle.

mercury；quality control charting；robust statistics；evaluation of measurement uncertainty

O657.31；TH744.12＋5

：A

：2095-1035（2015）02-0001-08

2015-02-02

：2015-03-04

环保公益性行业科研专项（201209015）、科技部重大仪器专项（2014YQ060773）资助

周瑞，男，工程师，主要从事固定污染源废气及环境样品中汞的监测研究。E-mail：Zhourui＠cneac.com＊通信作者：李玉武，男，教授。E-mail：liyuwu＠cneac.com

10.3969/j.issn.2095-1035.2015.02.001