小尺度效应对纳米开关吸合行为的影响
□陈博 □谭亮
兰州理工大学机电工程学院 兰州 730050
近年来随着纳机电技术的发展,作为纳机电系统基础元器件的纳米开关,受到了众多研究学者的青睐。纳米开关主要有两种类型,分别是悬臂纳米开关和固支纳米开关。这种纳米开关是一种类梁结构,它可以看作是由中间被电解质隔开的可移动臂和固定臂组成,当在可移动臂和固定臂之间施加外加电压时,静电力会使可移动臂和固定臂之间发生吸附行为[1]。
在宏观理论下,分子间的作用力,如范德华力和克什米尔力等,这些微小力都是忽略不计的。但当纳米开关的尺寸和分子处于同一数量级时,小尺度效应对于其机械性能的影响就显得非常重要[2]。曹共柏等[3]采用经典的分子动力学方法,分析了两端固支的纳米梁的力学行为特征,结果显示发热是纳米梁耗散机制的重要方式,即谐振能量转化为梁中原子的热运动动能。许科峰等[4]提出了几种基于MEMS(微机电系统)各向异性腐蚀技术的纳米梁制作方法,通过利用MEMS技术中材料与工艺的特性实现单晶硅纳米梁的制作。徐临燕等[5]基于原子力显微镜(AFM)测量了纳米梁的杨氏模量。近年来,由于需要合适的模型和理论来分析小尺度的机械器件和设备的机械性能,这就使连续介质力学的尺寸依赖理论受到了持续的关注[6]。严格来说,经典的连续介质力学并不适用于纳米级的纳机电系统元器件的分析,但是由于纳米级别的对照试验和分子动力学模拟不仅实施起来比较困难,而且成本昂贵[7],所以一些研究学者建立了若干非经典的连续理论,如非局部弹性理论[8]和偶应力理论[9],来解释纳结构的尺寸依赖行为。Beni Y T等[10]利用修正的偶应力理论和修正的Adomian分解方法,研究了纳机电系统中吸附行为的尺寸依赖特性,他们的研究结果显示,小尺度效应使纳米梁的临界吸附电压增大了。为了更为客观地反映小尺度效应对纳机电器件的影响,Yang J等[11]基于非局部理论对受外加电压和分子间作用力共同作用的纳米开关的吸附行为进行了研究,他们提出了一个线性分布载荷(LDL)模型,以获得悬臂和固支纳米开关封闭形式的解决方案,同时还发现,小尺度效应使悬臂纳米开关的吸合电压增大了,纳米开关固支纳米开关的拉入电压减小了。 Peng J S等[12]用一个适合边界条件的线性负载模型替代了LDL模型,并且基于Eringen的非局部弹性理论对纳米促动器的吸附行为重新进行了稳定性研究。此外,Wang B L等[13]提出使用应变梯度弹性理论来研究电驱动纳米梁的尺寸依赖性。Mousavi T等[14]基于Eringen的非局部弹性理论对纳米开关的吸合行为进行了分析。Wang K F等[15]通过差分正交方法研究了受静电力和分子间作用力作用的纳米开关的吸合稳定性。
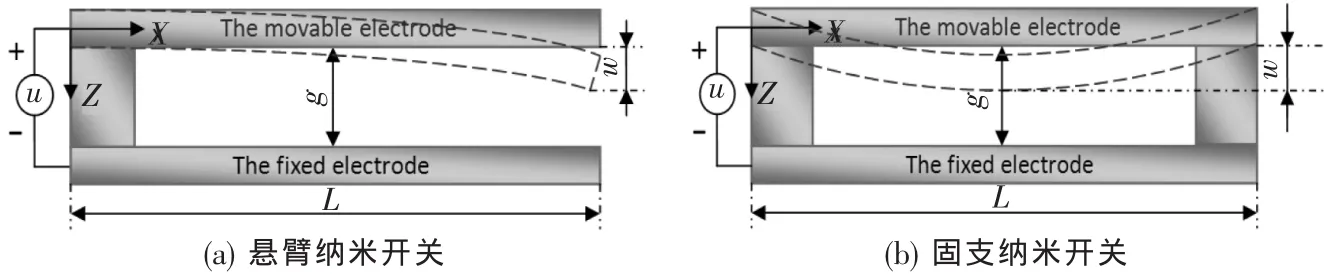
▲图1 纳米开关模型
为了进一步研究小尺度效应对纳米开关的影响,笔者引进了基于传统非局部理论和精确的能量变分法而获得的等效非局部理论,此理论建立在Eringen[16]的非局部弹性理论基础之上。笔者研究的主要内容是在得到受静电力和分子间作用力共同作用的纳米开关的控制方程后,利用解析法求解控制方程。
1 纳米开关模型
悬臂纳米开关和固支纳米开关都由一个可移动臂和一个固定臂组成,不同的是悬臂纳米开关可移动臂是类悬臂梁结构,而固支纳米开关可移动臂是类简支梁结构。在临界吸合电压作用下,可移动臂失稳而吸附在固定臂上,完成吸合行为。为研究纳米级结构的吸合行为,需要考虑范德华力、克什米尔力和静电力等微小力对其的影响。图1是纳米开关的模型。
在图1中,L为纳米开关的长度;U为外加电压;X和 Z为坐标轴;g为纳米开关固定臂 (The fied electrode)与可移动臂(The movable electrode)之间的初始距离;w为可移动臂变形后的挠度。
2 等效非局部理论模型
根据欧拉伯努利梁理论可知,沿坐标轴X方向的位移与应变之间的关系可表示为:

式中:εxx表示沿X轴向的正应变;t表示时间;z为沿Z轴方向的值。
为简化计算并更好地表达非局部纳米效应,引入非局部纳米参数τ:
式中:e0a是通过匹配实验和分子动力学模拟实验获得的材料常数。
在二维的情形下,通过格林公式得到的纳米开关的非局部应力与经典应力之间的关系为:

式中:σij为非局部应力;σij′为经典应力;▽为哈密尔顿算子。
当二维非局部理论问题过渡到一维问题时,式(3)可表示为:
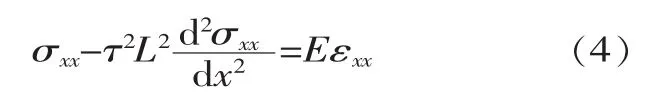
式中:σxx为轴向非局部正应力;E为弹性模量。
为了简化运算过程,对一些参数进行无量纲化:

进行无量纲化后,式(4)可表示为:
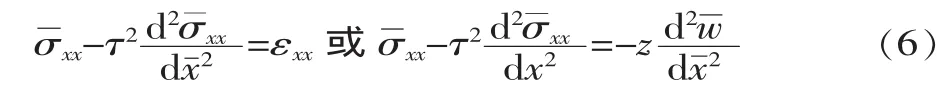
上式为二阶常微分方程,其通解可以表示为:

联立式(6)、式(7),可得积分常数 An的表达式:

一般当非局部参数τ逐渐趋于零时,非局部应力σxx就逐渐趋于宏观应力 σxx′,即所以,通解中的积分常数就必须为零,即 B1(z)=B2(z)=0。 进而,非局部应力的通解简化为:

有了非局部应力的表达式,就可以用它来表示可移动臂的应变能密度。在纳米开关变形后,单位体积内的能量密度μ为:

联立式(9)、式(10),单位体积内应变能的能量密度为:
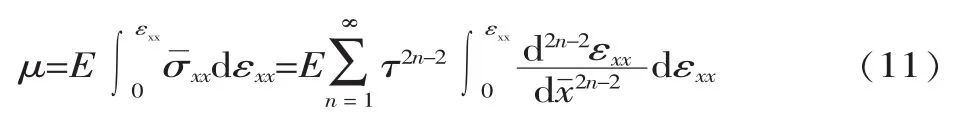
为了便于积分,把单位体积内应变能的能量密度分为三部分:

纳米开关的总应变能:

式中:U2为总应变能;V为总体积。
单位长度内所受到的克什米尔力[14]为:

式中:h=1.055×10-34Js,是普拉克常数除以2π所得;c=2.998×108m·s-1,为光速;b是可移动臂横截面的宽度。
可移动臂单位长度内受到的范德华力[15]为:

式中:A为哈莫克常数。
可移动臂单位长度上受到的静电力为:

式中:ε0=8.854×10-12F·m-1,是真空介电常数。
综上所述,可移动臂上所受到的均布载荷为:

由此均布载荷做的功W为:

等效非局部理论的理论基础是能量变分原理,通过这个过程可以得到等效非局部应变能、等效非局部弯矩和高阶的几何边界条件。为了能够应用能量变分原理,需要引入函数Z:

联立上述几个式子,可以得到:

式中:I为惯性矩。
由能量变分原理可知,能量函数的变分应为零,且在边界上的变分也为零,所以纳米开关的控制方程为:
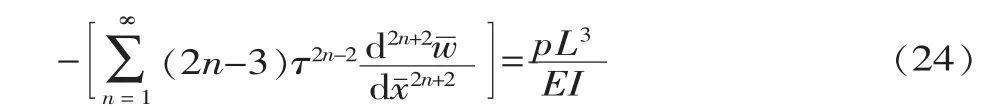
上式的通解为:

式中:Ci为待定常数,i=1~6。
高阶边界条件由自然边界条件和几何边界条件组成,其中自然边界条件也称为位移边界条件,是强约束的边界条件,必须在推导之前满足;几何边界条件也称为力的边界条件,是弱的边界条件,是在推导控制方程的过程中获得的。悬臂纳米开关的边界条件为:


▲图2 不同条件下纳米开关的挠度
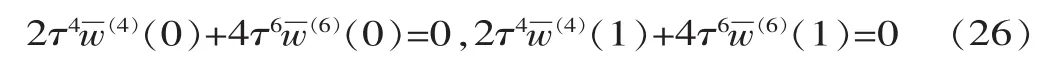
固支纳米开关的边界条件:

3 数值计算
如图2所示,描述了在不同条件下悬臂纳米开关和固支纳米开关可移动臂的吸合行为。图2(a)中,随着轴向坐标x值的增大,可移动臂上对应点的挠度也随之增大;图2(b)中随着x值的增大,可移动臂的挠度先达到一个峰值,而后逐渐减小到零。在图2(a)中,考虑非局部效应时的挠度要小于经典理论下的挠度,并且当非局部参数τ趋于零时,非局部理论的挠度曲线就与经典理论下的挠度曲线重合,这说明,非局部效应使悬臂纳米开关的挠度减小了,即悬臂纳米开关的弯曲刚度增大了。在图2(b)中,非局部效应使可移动臂的挠度较之于经典理论下有所增大。当非局部参数τ趋于零时,也回归经典理论,这说明,非局部效应使固支纳米开关的弯曲刚度减小了。
给定一个外加电压值,如u=1V,通过连续改变非局部参数τ的值,来获得相应的最大挠度。由图3可知,当非局部参数τ趋于零时,可移动臂的最大挠度就回归到经典理论,即始终保持为一定值。若非局部参数不为零,随着非局部参数的增大,悬臂纳米开关的最大挠度逐渐减小,而固支纳米开关的最大挠度则逐渐增大。
4 结论
综上所述,笔者基于等效非局部理论,研究了小尺度效应对悬臂纳米开关和固支纳米开关吸合行为的影响,即对两种纳米开关弯曲刚度的影响。为了更直观表达小尺度效应对纳米开关的影响,引入了非局部纳米参数,其值越大表示非局部效应越大,当其值趋于零时,非局部理论就回归到了经典理论。
研究结果显示,悬臂纳米开关和固支纳米开关的可移动臂越长,它们的吸合电压越小。对于同一长度的可移动臂,非局部参数越大,悬臂纳米开关的吸合电压越大,而固支纳米开关的吸合电压越小,但不会改变两种开关的吸合位移。而且,非局部效应对固支纳米开关的影响比对悬臂纳米开关的影响要大。两种纳米开关的计算结果,都是通过与经典理论的计算结果进行比较来判断其结论的准确性和合理性的。非局部效应使悬臂纳米开关的最大挠度和吸合电压比经典理论下的最大挠度和吸合电压减小了,却使固支纳米开关的最大挠度和吸合电压比经典理论下的最大挠度和吸合电压增大了,也就是说,非局部效应使悬臂纳米开关的弯曲刚度变大了,却使固支纳米开关的弯曲刚度变小了。

▲图3 非局部效应对纳米开关最大挠度的影响
[1] Taghavi N,Nahvi H.Pull-in Instability of Cantilever and Fixed-fixed Nano-switches [J].European Journal of Mechanics A/Solids,2013,41:123-133.
[2] Wang G F,Yang F.Postbucking Analysis of Nanowires with SurfaceEffect[J].JournalofAppliedLetters,2011,109(2):1-3.
[3] 曹共柏,焦继伟,陈云飞,等.单晶硅纳米梁的分子动力学模拟[J].传感技术学报,2006,19(5):1686-1688.
[4] 许科峰,于海涛,杨永亮,等.几种基于MEMS的纳米梁制作方法研究[J].传感技术学报,2007,20(9):1971-1976.
[5] 徐临燕,栗大超,胡小唐,等.基于原子力显微镜的纳米梁杨氏模量的测量[J].天津大学学报,2007,40(7):816-820.
[6] Ou Z Y,Pang S D.Fundamental Solutions to Hertzian Contact Problems at Nanoscale [J].Acta Mechanics,2013,224(4):109-121.
[7] Murmu T,Pradhan S C.Small-scale Effect on the Free Inplane Vibration of Nanoplates by Nonlocal Continuum Model[J].Physica E,2009,41(6):1628-1633.
[8] Eringen A C.On Differential-equations of Nonlocal Elasticity and Solutions of Screw Dislocation and Surface-waves[J].Journal of Applied Physics,1983,54(3):4703-4710.
[9] Ejike Uwadiegwu B C O.The Plane Circular Crack Problem in the Linearized Couple-stress Theory [J].International Journal of Engineering Science,1969,7(1):947-961.
[10] BeniY T,Abadyan M R,NoghrehabadiA,etal.Investigation of Size Effect on the Pull-in Instability of Beamtype NEMS underVanderWaalsAttraction [J].Procedia Engineering,2011,10(1):1718-1723.
[11] Yang J,Jia X L,Kitipornchai S,et al.Pull-in Instability of Nano-switches Using Nonlocal Elasticity Theory[J].Journal of Physics D:Applied Physics,2008,41(3):295-302.
[12] Peng J S,Luo G B,Yang L,et al.Pull-in Instability Behaviour of Nanoscale Actuators Using Nonlocal Elasticity Theory [J].Advanced Materials Research,2012,468 (1):2755-2758.
[13] Wang B L,Zhou S J,Zhao J F,et al.A Size-dependent Kirchhoff Micro-plate Model Based on Strain Gradient Elasticity Theory [J].European Journal of Mechanics A/Solids,2011,30(4):517-524.
[14] Mousavi T,Bornassi S,Haddadpour H,et al.The Effect of Small Scale on the Pull-in Instability of Nano-switches Using DQM [J].InternationalJournalofSolids and Structures,2013,50(2):1193-1202.
[15] Wang K F,Wang B L.Influence of Surface Energy on the Non-linear Pull-in InstabilityofNano-switches [J].International Journal of Non-Linear Mechanics,2014,59(1):69-75.
[16] Eringen A C.Nonlocal Continuum Field Theories [M].New York:Springer-Verlag,2002.
[17] Lamoreax,S K.The Casimir force:Background,ExperimEnts,and Applications [J].Reports on Progress in Physics,2005,68(1):201-236.
[18] Israelachcili,Jacob N.Intermolecular and Surface Forces[M].3rd ed,Amsterdam:Elsevier Inc,2011.
