独立型微电网中主电源逆变器的控制算法

李凯，曾斌，，唐刚，徐红兵，赵霁

（1.电子科技大学自动化工程学院，成都 611731；2.东方电气集团电力电子与控制事业部，成都 611731）

在能源需求和环境保护的双重压力下，分布式发电技术获得了越来越多的重视与应用。将分布式电源以微电网的形式接入大电网并网运行或者形成孤岛独立运行，与大电网互为支撑，是发挥分布式发电系统效益的有效途径[1-3]。微电网分为两种类型：联网型微电网和独立型微电网。独立型微电网不与常规电网相连接，利用自身的分布式能源满足微网内负荷的需求。当电网内存在可再生分布式能源时，常常需要配置储能系统作为主电源稳定电网电压的幅值和频率，保持电源与负荷间的功率平衡，并充分利用可再生能源。因而，用于储能系统与电网接口的离网型三相逆变器要求在不同负载条件下其输出电压幅值和频率在一定范围内保持恒定。

简单的PI线性控制很早就被应用于离网型逆变器的控制中，但在两相静止坐标系下的PI控制无法对给定的正弦交流信号进行无静差跟踪。同步旋转坐标系下的PI控制虽然可以实现对正弦交流信号的无静差控制，但是需进行坐标转换和解耦运算，增加控制系统的复杂度，另外对电压的谐波成分进行控制时，需多次坐标转换，且只能对指定次进行补偿[4-5]。比例谐振控制由于在谐振频率处不引入相位延时，且有很大增益，可对谐振频率的正弦信号实现无静差控制，且具有良好的动态性能，在逆变器的控制中得到广泛应用，但无法解决死区和非线性负载等引起的电压谐波问题，导致输出电压发生畸变[6-7]。为抑制谐波，重复控制器被引入到逆变器的输出波形控制中，可有效地提高逆变器输出电压波形质量[8-11]，但由于重复控制器的极点位于虚轴上，具有临界稳定特性，文献[12]提出了具有前馈和反馈环节的改进重复控制器。逆变器常采用LC和LCL滤波，滤波器固有的谐振特性会造成系统不稳定，为了抑制谐振，常采用无源阻尼和有源阻尼的方法[13-14]，但无源阻尼会引起系统损耗增加，同时也带来散热问题；有源阻尼会需要增加电容电流反馈，增加系统成本。

本文首先在分析独立型微电网主电源逆变器的数学模型的基础上，提出一种电压外环、电流内环的双闭环控制算法。电压外环采用重复控制-比例谐振控制复合的控制算法，电流内环采用电感电流反馈控制。其次基于传递函数分析控制系统的稳定性，进而进行控制参数设计。最后通过仿真和平台实验验证控制算法的可行性和有效性。

1 离网型三相逆变器数学模型

本文采用如图1所示的LCL型三相半桥逆变器拓扑结构，其中，L和Lo分别为交流侧和负载侧的电感，R和Ro分别为交流侧和负载侧电感的寄生电阻，C为交流滤波电容，采用星形连接。

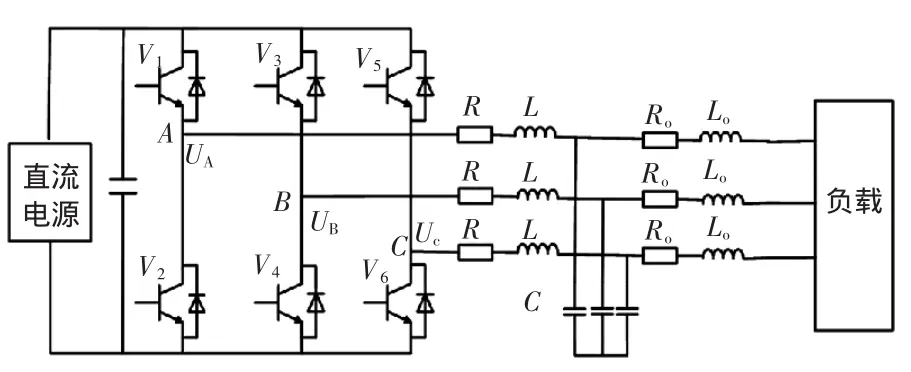
图1 三相逆变器电路拓扑结构Fig.1 Topology of three-phase inverter

假设三相负载平衡，则图1中三相LCL滤波器的每一相工作状态相同，因此可从三相电路拓扑结构图中提取出简化的单相电路拓扑结构来分析，根据基尔霍夫电压电流定律，可以得到

式中：Uo和U分别为逆变器负载电压和交流侧电压；io和i分别为逆变器负载电流和交流侧电流；Uc为电容电压；Z为负载阻抗。由此，可以得到Uo、U和io的关系式为

式中：Gl=Ls+R；Glo=Los+Ro；Gc=Cs，s为拉普拉斯运算符。

将输出电流io视为扰动输入，可以得到逆变器输出电压Uo同逆变器交流侧电压U的传递函数为

式（3）表明，控制对象是一个典型的二阶系统，其谐振频率为，阻尼比为由于电感的寄生电阻很小，因此系统在谐振频率处接近自由谐振。

2 基于复合控制的双环控制算法

本文提出一种适用于离网逆变器的双闭环控制策略，包括一个基于重复-PR复合控制的电压外环和一个基于比例环节的电流内环，系统控制结构框图如图2所示。

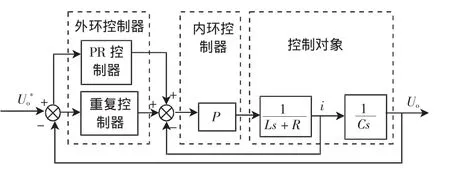
图2 双闭环控制结构框图Fig.2 Block diagram of dual-loop control strategy

2.1 电感电流反馈内环

双闭环控制结构中的电压外环是对输出电压进行控制，对于电流是间接控制，加入电流内环是为了对电流进行直接控制；对于LCL型滤波器的谐振问题，通过电感电流反馈可以增大系统阻尼，达到抑制谐振的效果。引入电流内环后系统的传递函数变为

式（4）加入电流内环后，谐振频率为ωn=，阻尼比为因此，电流内环的加入，等效于在电感寄生电阻中增加P值大小的电阻，增加系统阻尼，增强系统的稳定性。

2.2 重复-PR复合控制电压外环

重复控制技术的思想来至于内模控制原理，利用扰动的重复性来逐周期修正输出信号。重复控制用于逆变器控制可以将非线性负载引入的周期性重复出现的扰动信号消除，来改善输出电压的波形质量。在两相静止坐标系下，用于逆变器控制的改进型重复控制器[12]控制结构如图3所示，其中，K为比例常数，τ为低通滤波器时间常数，Kf为反馈和前馈系数，T为电网的基波周期。低通滤波器是为了削弱高频环节的积分，比例常数主要是为了限制系统的积分，增强系统的稳定性。

图3 重复控制器控制结构Fig.3 Block diagram of repeative control strategy

可以得到其传递函数为

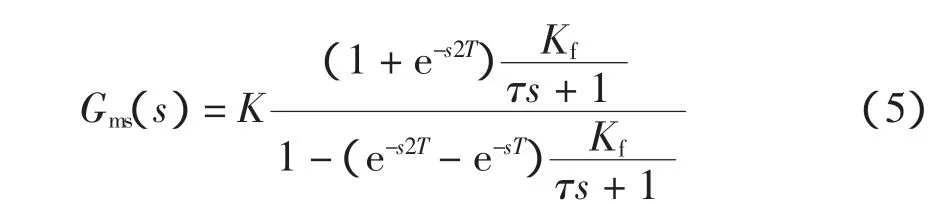
PR控制是一种用比例环节与广义积分环节并联的一种控制方式，比例环节可以提高系统的响应速度；而广义积分环节则是在设定频率形成谐振，使该谐振点有接近于无限大的增益，实现对给定正弦信号的“零误差”跟踪，只要令谐振控制器的谐振频率等于电网电压基波频率，就能够对基波的“无静差”跟踪。本文采用改进的PR控制器，其传递函数为

式中：Kp和Ki为PR控制器参数，Kp为比例常数，Ki为积分常数；ω为基波角频率；ωc为截止频率，改进PR控制器可以有效地增大系统的带宽，降低控制系统对电网频率轻微变化的敏感度。

通过以上分析可知，重复控制和PR控制具有互补性，PR控制实现对基波电压的无静差跟踪，重复控制实现对电压谐波的抑制。

3 控制参数设计

重复控制和PR控制复合并联控制的控制器参数设计，可以先进行PR控制电压外环和P控制电流内环参数设计，再进行重复控制参数设计。

3.1 PR控制和电流内环控制

由式（4）和式（6）可以得到，采用PR外环-P内环的双闭环控制的开环传递函数为

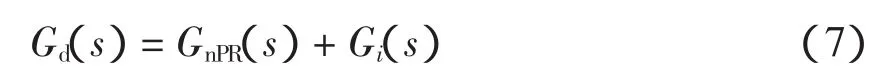
系统的闭环传递函数为

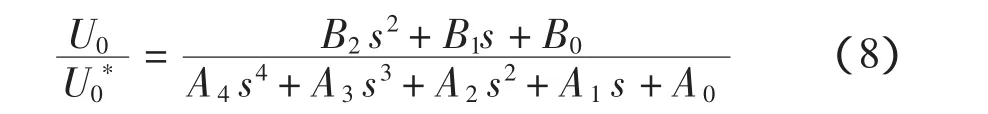
式中：B2=KpP；B1=2Pωc（Kp+Ki）；B0=ω2Kp；A4=LC；A3=2LCωc+（R+P）C；A2=LCω2+2ωc（R+P）·C+KpP+1；A1=ω2（R+P）C+2ωc（KpP+KiP+1）；A0=ω2（Kp+1）。

对应的特征方程为

根据劳斯判据由此可以得到使得系统稳定的Kp、ωc、Ki、P参数的关系式，选取控制参数时必须满足系统稳定的关系式为

本文研究的主电源逆变器的主电路参数L=0.16mH，R=0.06Ω，C=0.51μF（对应LCL谐振频率为25 kHz），本文选取的控制参数为Kp=0.04，ωc=15，Ki=10，P=2.5可以得到系统的闭环函数零极点分布如图4所示。可知零极点都在单位圆内，系统稳定。

图4 闭环传函零极点Fig.4 Root locusof closed loop control

3.2 重复控制

如式（5）含有前馈和反馈环节的重复控制器，只需设计K、τ和Kf3个参数。

低通滤波器主要是要削弱高频的积分效果，同时考虑到系统的控制带宽以及LCL滤波电路的高频谐振点（本文对应25 kHz），低通滤波器的截止频率都要小于此值，这里取低通滤波器的截止频率为500Hz，则时间常数τ为1/2πf=3.18×10－4s。

含前馈和反馈环节的重复控制器等效于无数个PR中的谐振环节并联，对于反馈和前馈系数Kf，加入Kf后，令0

对于比例常数K，目的是为了限制重复控制器的无限累加，通过牺牲静差来提高系统的稳定性，一般K值取略小于1的常数。同时，要考虑系统的稳定性。重复控制器等效于PR控制器的谐振部分，而且谐振频率是基波频率的整数倍，为了分析对系统稳定性的影响，只考虑重复控制外环和电流内环，由式（4）及式（5）可以得到，其开环传递函数为

根据判断系统稳定的小增益定理，可以推出系统稳定的一个含有K值的不等式。小增益定理判定系统稳定的条件对于任意ω，|Grd（jω）H（jω）|<1，系统的H（jω）为1，所以要让本系统稳定的充分条件为

对于任意ω都成立。这里取Kf值为0.8，τ值为3.18×10－4，代入式（10）得到的K取值范围为0～1.25，因此本文取K为0.9。

4 仿真和平台实验分析

为了验证本文控制策略的可行性和有效性，在Matlab/Simulink中搭建离网逆变器系统仿真模型进行仿真和搭建平台实验两个方面的验证。

4.1 仿真分析

仿真模型的系统参数为：主电路参数L=Lo=0.16mH，R=Ro=0.06Ω，C=0.51μF，电压给定值为相电压有效值U=220 V，频率给定值为工频f=50Hz，开关频率fk=10 kHz。仿真波形如图5所示。

图5 仿真波形Fig.5 Simulation waveform s

图5中，图（a）为逆变器输出的三相交流电压波形；图（b）为不可控整流电路负载条件下的a相电压电流波形，此时的电压THD为4.3%，电压偏差为0.6%；图（c）为空载条件下的电压电流波形，电压THD为4.32%，电压偏差为1.1%；图（d）为有功功率为30 kW的阻性负载条件下的电压电流波形，电压THD为1.52%，电压偏差为0.5%；图（e）为有功功率为30 kW，无功功率为10 kvar的负载条件下的电压电流波形，电压THD为1.54%，电压偏差为0.5%。可知本文提出的双闭环控制策略可以有效地实现电压波形的稳定输出，适用于不同负载情况，而且实现了对电压谐波的有效抑制。图（f）～（h）分别为系统负载跳变的功率波形、电压电流波形和电压偏差百分比，跳变过程中，电压和电流始终保持同相，而且半个周期内即可达到稳定，电压偏差都小于5%，说明本文采用双闭环控制策略可以保持系统的稳定运行，且具有良好的动态性能。

为了验证控制策略中重复控制器和电流内环的作用，仿真实验做了对比仿真，仿真结果如图6所示。

图6 电流内环和重复控制对比仿真结果Fig.6 Simulation results of inner current control and outer repetitive control

图6（a）和（b）仿真的负载条件为有功功率为10 kW，无功功率为10 kvar。对比图6（a）和（b）可知，没有电流内环时，逆变器输出电压已经不可控，超过了500 V，且呈发散趋势；而有电流内环的电压波形依然稳定可控，加入电流内环可以增加系统稳定性。图6（c）和（d）仿真的负载条件为不可控整流电路的非线性负载。对比图6（c）和（d）可知，加入重复控制器后，可以有效地减少20～40次的高频谐波，谐波含量从5.59%降到了4.30%，提高输出电压的波形质量。

4.2 平台实验分析

实验平台的参数同仿真平台所用参数。实验波形如图7所示，其中图7（a）为满载50 kW时a相电压电流波形，电压THD为3.5%，电压偏差为0.5%；图7（b）和（c）为空载和满载间切换的电压电流波形，图中空载时的电流属于实验平台所接变压器的励磁电流，从放大区域下方的放大图可以看出，本策略在实验平台上同样可以实现负载的平稳切换，且在半个周期内达到稳定，具有良好的稳态和动态性能。

图7 平台实验波形Fig.7 Experience result waveforms

5 结语

本文提出了一种独立型微电网中主电源逆变器的双闭环控制算法，通过理论分析、仿真及平台实验分析可以得到，采用该算法的主电源逆变器电压控制最大静态偏差为0.6%，最大电压总谐波失真为4.3%，且在非线性负载和负载突变下有良好的动态响应，可在独立微电网中采用逆变器接口的主电源中广泛应用，具有良好的工程指导作用。

[1]吴蓓蓓，苏建徽，张军军，等（Wu Beibei，Su Jianhui，Zhang Junjun，et al）.用于微电网孤岛运行的逆变电源控制方法（Control strategies of inverter in microgrid island operation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（1）：1-5.

[2]韩肖清，曹增杰，杨俊虎，等（Han Xiaoqing，Cao Zengjie，Yang Junhu，et al）.风光蓄交流微电网的控制与仿真（Control and simulation of wind-PV-battery AC microgrid）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（3）：50-55.

[3]潘远，李培强，李欣然，等（Pan Yuan，Li Peiqiang，Li Xinran，et al）.考虑主从控制策略的微电源逆变器设计（Design of micropower inverter considering master-slave control strategy）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（3）：25-30.

[4]Rowan T M，Kerkman R J.A new synchronous current regulator and an analysis of current regulated PWM inverters[J].IEEE Trans on Industry Applications，1986，22（4）：678-690.

[5]Haque M E，Muttaqi K M，Negnevitsky M.Control of a stand alone variable speed wind turbine with a permanent magnet synchronous generator[C]//IEEE Power&Energy Society General Meeting.Pittsburgh，USA，2008.

[6]Huang Long，Li Bin，Lyu Zhengyu，et al.PR controller for grid-connected invertercontrolusing directpole placement strategy[C]//IEEE 21st International Symposium on IndustrialElectronics.Hangzhou，China，2012：469-474.

[7]Shen Guoqiao，Zhu Xuancai，Zhang Jun，et al.A new feedback method for PR current control of LCL-filterbased grid-connected inverter[J].IEEE Trans on Industrial Electronics，2010，57（6）：2033-2041.

[8]粟梅，王辉，孙尧，等（Su Mei，Wang Hui，Sun Yao，et al）.基于改进重复控制器的三相四线逆变器设计（Design of three-phase four-leg inverter based on modified repetitive controller）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（24）：29-35.

[9]Chen S，Lai Y M，Tan S-C，et al.Analysis and design of repetitive controller for harmonic elimination in PWM voltage source inverter systems[J].IET Power Electronics，2008，1（4）：497-506.

[10]刘飞，邹云屏，李辉（Liu Fei，Zou Yunping，LiHui）．基于重复控制的电压源型逆变器输出电流波形控制方法（The repetitive control algorithm based current waveform correction for voltage source inverters）[J]．中国电机工程学报（Proceedings of the CSEE），2005，25（19）：58-63.

[11]王斯然，吕征宇（Wang Siran，Lyu Zhengyu）.LCL型并网逆变器中重复控制方法研究（Research on repetitive control method applied to grid-connected inverter with LCL filter）[J].中国电机工程学报（Proceedings of the CSEE），2010，30（27）：69-75.

[12]Escobar G，Leyva R J，Martinez P R，et al.A repetitivebased controller for the boost converter to compensate the harmonic distortion of the output voltage[J].IEEE Trans on Control Systems Technology，2005，13（3）：500-508.

[13]张宪平，周飞，赵波，等（Zhang Xianping，Zhou Fei，Zhao Bo，et al）.LCL滤波的风电网侧变流器有源阻尼策略（Active damping strategy for grid-side converter with LCL filter in wind power system）[J].电力自动化设备（Electric Power Automation Equipment），2010，30（6）：11-15.

[14]张学广，刘义成，王瑞，等（Zhang Xueguang，Liu Yicheng，Wang Rui，et al）.一种新型的PWM变换器LCL滤波器有源阻尼控制策略（A novel active damping control strategy for PWM converter with LCL filter）[J].电工技术学报（Transactions of China Electrotechnical Society），2011，26（10）：188-192.