顺应学生思维,让数学课堂柳暗花明
江苏扬州大学教科院附属杨庙小学(225125) 焦 凤
在传统教学中,教师常常认为学生所知甚少,因而会对教学难点反复强调,甚至“满堂灌”、“满堂问”,但效果并不理想。由此,小学数学教学的重点,就是要顺应学生的思维,找准学生已有认知和所学知识的差距,搭建沟通桥梁,疏通教与学的障碍。
一、把握学情,顺应生活经验
在小学数学教学中,教师不能忽视学生的已有经验,更不能武断地剥夺学生的已有认知,直接进行主观讲授,而是要借助已有经验,把握学生学情,为学生架设新知探究的平台。
例如,教学“三角形的高”时,很多学生通常是将垂直于水平面的纵向跨度称为高,这种认知与几何图形中的高是有本质区别的。因此,教师可以将这种经验认知作为突破口,先出示两个三角形让学生判断:哪个更高?为什么?
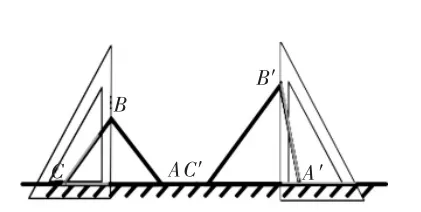
图1
有的学生用手掌水平放在三角形的顶点上,以到达掌心的高度为标准,衡量哪个三角形更高;也有学生沿着高的位置进行比划。此时我拿出三角板,让学生比划出三角形的高,并将三角板倾斜,启发学生思考:要怎样放?三角板的边和哪里垂直?如何垂直?学生体会到必须要将竖着的边和底边垂直才行。紧接着,我转动三角形,将底边AC改变为A′C′,边BC改变为B′C′,再将边AB改变为A′B′(如图1)。学生由此获得明确认知:从三角形的任意一个顶点到对边的垂线段,就是三角形的高。
这个引导过程,有效突破了学生原有生活经验对新知的干扰,促进了学生的认知从垂直于水平底面这一标准图示,向从点到对边的垂线段这个变式图示的提升,实现了高的本质的抽象和确立。
二、沟通联系,顺应现实起点
在小学数学教学中,教师要找到学生的原有认知与新知之间的矛盾点进行教学设计,在此基础上,还要顺应现实起点,进一步分析研究,展开逻辑推理,将所学新知和原有认知进行比对,沟通新旧知识之间的联系,找到需要增量的部分进行难点突破,帮助学生破除干扰,实现新知建构。
例如,教学“小数的初步认识”时,为了让学生理解小数的含义,并初步感知小数与分数的有机转换,可出示习题:课桌高80厘米,怎样用米做单位来表示?学生有的认为可以用、0.8表示,有的认为可以用表示。显然,在这个习题检测中,学生之所以出现认知分歧,主要是有关分数和小数的基础知识并没有打牢。为此,我从这一现实起点入手:1分米怎样用米表示?3分米呢?4厘米怎样用米表示?根据已有认知经验,学生通过直观的米尺观察,顺利建构了新旧知识的联系,认为1米=10分米,那么1分米就是米,也可以写成0.1米;3分米就是米,也就是 0.3米;1米=100厘米,那么 4厘米就是米,也就是 0.04米。
教师根据学生的认知现实,找到教学起点,并顺应这一现实问题,借助长度单位这个背景,将分数和小数的关系进行沟通,通过旧知和新知有机融合,带领学生沟通新旧联系,由此跨越认知中的思维误区。
三、激发潜能,顺应心理需求
在小学数学教学中,教师要顺应学生的心理需求,善加捕捉亮点,给予尊重和支持,聆听学生的所思所想,及时捕捉意外生成,激发学生的潜能。
例如,苏教版“圆柱和圆锥”的习题:圆柱形容器的侧面积是56.52平方分米,底面半径是3分米,求这个圆柱形容器的体积。这道题并不复杂,大部分学生都认为,只要求出圆柱体的高“56.52÷(2×3.14×3)=3(分米)”,然后利用体积公式“底面积×高”就可以了(3.14×32×3=84.78(立方分米)。但在解题时,有学生列出了不同的算式,也得到了同样的结果,很多学生认为答案只是巧合,并没有道理可言。我鼓励这位学生说出自己的想法,他认为,在圆柱体面积推导公式中,圆柱体能够被拼成一个近似的长方体,如果将这个长方体放在桌面上,那么圆柱体的侧面的一半就是长方体的底面,也就是圆柱体的底面积(56.52÷2),由此就可以得到:圆柱体的体积=侧面积÷2×高,56.52÷2×3=84.78(立方分米)。显然,通过教师的引导,学生的心理需求得到了满足,创新的动力被激发,为思维发展奠定了基础。
显而易见,尊重学生的已有起点,顺应学生思维,把握教学起点,能让数学课堂柳暗花明,这是一条非常值得尝试的有效路径。

