化归思想在高中函数中的应用

王婷婷

（山东省东营市胜利第十三中学）

在解析数学题时，通常会运用化归思想的思维策略，是因为运用它时会将数学问题变得非常简单，能够快速地将数学题解析出来。所以化归思想在高中数学解析中起着非常重要的作用。

一、化归的特点

复杂性和多向性是化归的两大特点。在条件适当时利用化归思想进行转换，是数学题求解成功的关键因素。因此，条件转换，不但包括针对数学题中所含有的条件进行转换，还将结论部分的转换包含其中，同时无论是外在形式还是内部结构都可以实现转换，所以化归表现出化归的多向性。纵向看数学这门课程，一般可以将各类的解题技巧或者形式多样的数学方法运用在化归思想解数学题当中，所以将化归思想运用在高中函数中，具有多样性。

化归还具有复杂性，这主要表现在，将亟待解决的函数题用a来表示，使用化归思想将a 向学过的内容b 转换，利用b 可以很容易地将问题解决，然而在解决完b 问题时，还需要将b 还原成为a 的形式，也就是得到a 函数问题的结果。在解决a 问题时比较繁琐，但是能够通过自己掌控的步骤来求出正确的解。根据解析得知化归具有复杂性。

二、在高中函数中化归思想的应用

（一）从未知转换为已知

为了快速解决函数中的未知问题，一般我们是用化归思想解决，运用该思路将已知与未知形成相关性，然后再运用熟悉的解题思路来解析问题。该种思路能够快速地解决函数问题，通常在三角函数中求得最值时，就是利用该方法将未知问题转化为熟悉的解题思路，进行“曲线”解决该问题。下面就来举例说明：

将y=sinx+cosx+sinx·cosx 这一函数的最值求出来：

解题思路为：可以将m 这一代换值引入函数中，m=sinx+cosx，那么可以得出sinx·cosx=·（m2-1）。

运用这样的化归思想之后，就可以将看似复杂的函数，转化为学生熟悉的二次函数，因此求解就较为简单，将刚才化归的函数代入y 公式中，可以得出：

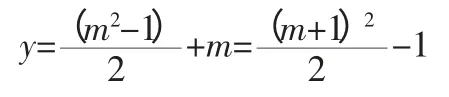
根据该题的解析，可以迅速地将看似复杂的函数进行求解。

（二）使用图形将函数解析题使用化归思想转化

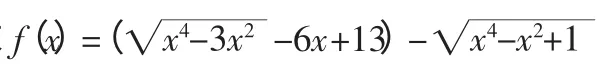
因此转化成为上面的函数时，就可以当作点A（3，2）到抛物线上的某个点P（x、x2）点的距离和B 点（0，1）到P 点的距离之差，如下图所示。

当PB 和PA 之间的间隔不等于AB 时，P0在AB 延长线上时，所设置的函数最大值为|AB|，当求出A 点和B 点的坐标时，就可以求出函数的最大值为。

该类型的题目通常都会采用化归思想的方式将策略向图形转换，然后再利用图形或者增添辅助线的方式来将结果算出，这是学生在解函数题时的一个捷径。即便很复杂的函数题，也都不会离开此规律，在注入化归思想的理念之后，就会很快地解决函数题。

此外，在高中函数中运用化归思想，还有特殊到普通的化归方法、常量与变量之间的化归、相等与不等的化归等。数学思想在高中数学函数学习中起着非常重要的作用，所以只要将化归思想融会贯通，学生在接触任何新型题材的函数题时，都不会被难倒。

学生在听完课后，感觉自己能够懂得教师的解题思路，却无法正确地将类似习题解答正确。究其原因在于没有熟练掌握教师所教授的教学思路。因此，在函数题解析中，学生只有熟练掌握化归思想，才能够在考试中游刃有余，立于不败之地。

［1］代琼.化归思想在高中函数教学中的应用研究［J］.数理化学习：高中版，2014（11）：10-11.

［2］周炎龙.化归思想在高中数学中的体现和教学［D］.河南师范大学，2013.