灰色预测模糊PID控制在调节阀智能定位系统中的应用

　，

(1. 北京航空航天大学 仪器科学与光电工程学院， 北京　100191； 2. 微纳测控与低维物理教育部重点实验室， 北京　100191)

引言

气动调节阀是过程控制系统中用动力操作去改变流体流量的装置，它是一种重要的执行器，广泛应用于石油、化工、冶金、造纸等行业的工业自动化过程。由于气动调节阀内部结构特性，使得调节阀本身存在一些固有的非线性特征，如死区、回差、滞后等。在调节阀的工作过程中，环境压力、流体特性、温度等条件可能随时发生变化，对象特性参数也会随之发生相应改变，因此调节阀系统同时具有时变性的特点。此外，气动调节阀多用于工业多干扰环境中，对流量控制的精度及系统的稳定性要求很高，这就要求气动控制系统必须具有较好的鲁棒性与抗干扰能力。因此，对于气动调节阀这种具有大惯性和滞后、参数不定常、易受外界干扰的非线性时变系统，很难建立精确的数学模型，其控制问题一直是气动控制系统的难点。文献[1]提出了一种基于误差相平面分析的PID控制和整定的算法，通过误差相平面分析提高偏差的辨识能力，但是单纯的PID算法在干扰和环境变化时易导致控制品质的降低。文献[2]介绍了一种结合Smith预估及模糊自适应PID的算法，利用Simth预估补偿控制对象纯滞后性，用模糊PID算法满足参数的不确定性和在线调整的适应性，但是当Smith预估模型和实际对象不匹配时，会对误差的变化异常敏感，使控制效果变差。

本研究在深入研究灰色预测理论和模糊控制算法的基础上，设计了一种以单片机作为控制核心，同时基于灰色预测模糊PID算法的成本低、控制精度高、自适应能力强、实时性好的调节阀智能定位系统。该系统的控制器以模糊整定PID环节来提高系统调节精度、改善动态性能，再结合灰色预测模型实施“超前控制”来抑制系统滞后性引起的阀门定位不准以及稳定性较差等问题，从而增强控制效果，提高调节阀定位系统的控制精度。

1　调节阀智能定位系统

本研究提出的调节阀智能定位系统是以单片机为核心并融合灰色预测模糊PID复合控制算法的一种控制系统，图1是其整体架构。

如图1所示，由外部给定的指令信号经取样单元处理，作为阀位设定值信号输入；由位置反馈单元检测到的阀门位置的真实值，作为阀位反馈值信号输入。两路输入信号经过单片机内部的12位A/D转换器最终转变为单片机可接收的数字电压信号。中央处理单元将两路信号经必要处理后比较得误差信号e，并通过复合算法对e值进行处理，输出相应的电控信号。通过驱动电路使I/P转换单元电磁阀进行相应的进/排气操作，完成电气转换以驱动执行机构的阀杆上下移动，从而控制阀门的开关状态及行程，使其迅速动作到预定位置，提高控制系统的灵敏度和精确性。

2　复合算法控制器设计

2.1　控制器结构

灰色预测模糊整定PID控制算法是一种优势互补的控制方法[3，4]，适用于阀门位置的闭环控制。针对本系统设计的复合算法控制器结构如图2所示。

图2中模糊控制器的两个输入分别为阀门位置的预测偏差和预测偏差的变化率。灰色预测模型设置在反馈回路中，系统偏差为设定值与输出的h步预测值之差。调节阀智能定位系统的位置反馈单元检测到阀门位置的真实值，由灰色预测模型对当前时刻k之前的n个连续采样阀位真实值数据进行处理得到k+h时刻的预测值，该预测值作为阀位反馈值信号，与设定值比较得到阀门位置的预测误差。单片机的CPU接受该误差信号后， 将阀位预测误差及其变化率作为模糊整定控制器的输入信号，模糊控制器将它们分成若干个模糊集合，通过模糊化、模糊规则、 去模糊化等步骤[5]对PID控制器的参数进行在线整定，并输出控制量ΔKP、ΔKI、ΔKD到PID控制器，使参数能够根据阀门的真实状态进行调节。

图1　调节阀智能定位系统整体架构

图2　复合算法控制器结构框图

2.2　灰色预测模型的应用

灰色预测模型可通过对系统输出数据序列的处理，预测未来发展趋势，从而确定相应的控制策略对系统进行“超前控制”[6]。系统采用一阶单变量灰色预测模型GM(1,1)，取灰色预测的数列长度为5，即设所测的系统输出时间序列为：

y(0)(k,1),y(0)(k,2),y(0)(k,3),

y(0)(k,4),y(0)(k,5)

(1)

对序列各时刻数据累加生成(AGO)新数列，以减弱原始数据序列受不确定因素干扰的影响。新生成的数据列为：

(2)

对序列y(1)(k,i)的每个相邻数据分别求取均值，得到z(1)(k,i)：

z(1)(k,i)=0.5[y(1)(k,i)+y(1)(k,i-1)](3)

故得模型GM(1,1)的微分方程：

y(0)(k,i)+az(1)(k,i)=bi=1,2,3,4,5(4)

相应的白化方程为：

(5)

其中，a为发展系数；b为灰色作用量。

对模型参数a、b进行辨识，由最小二乘法可推出：

(6)

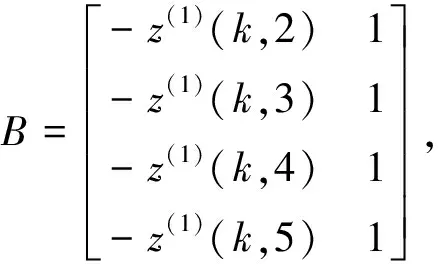
Y=[y(0)(k,2),y(0)(k,3),y(0)(k,4),y(0)(k,5)]T

故白化方程的解为：

(7)

对上式离散化，得微分方程的时间响应序列：

(8)

将y(1)(k+1)经累减生成(IAGO)有：

y(0)(k+1)=y(1)(k+1)-y(0)(k)

(9)

经递推法可得原始输出数据列的h步向前预测值：

(10)

经以上步骤即可利用反馈回路中的灰色预测模型GM(1,1)得到k+h时刻的输出预测值， 用预测误差e(k)=x(k)-y(k+h)代替原测量误差e(k)=x(k)-y(k)，提高阀位控制的实时性和准确性。其中，输出向前预测步数h依系统滞后性的大小适当选取，滞后性或惯性若大则预测步数也选大些，反之则选小些。

2.3　模糊控制算法的实现

模糊控制法是一种智能控制方法，它可以不需要被控对象的数学模型，直接应用于非线性系统[6]。PID控制是一种广泛应用于工业控制领域的算法，但其控制参数不能在线整定，影响控制的效果。可将模糊控制法和常规PID控制相结合，利用模糊规则对PID、参数在线整定[7,8]，提高阀门位置定位的精度。

将单片机采样得到的数字化的阀门位置偏差及其变化率模糊化得到E和EC，并以PID参数的修正量ΔKP，ΔKI，ΔKD为输出，应用模糊集合理论建立KP、KI、KD参数与E、EC之间的函数关系，最后PID控制器输出控制量到电气转换单元促使调节阀阀杆进行相应动作。

调节阀智能定位系统中单片机内部ADC参考电压为2.5 V，转换精度12位。因此，控制器的输入偏差E的基本论域为[0,212]，偏差变化率EC的基本论域为[0,2000]，将它们的基本论域均化成离散论域[-6,6]，并选取负大、负中、负小、零、正小、正中、正大{NB、NM、NS、ZO、PS、PM、PB}7个语言变量值档次。相关文献表明，采用形状较尖的隶属度函数曲线，其模糊子集分辨率较高，控制灵敏度较好。因此，E和EC采用如图3所示的三角形隶属度函数曲线。

将ΔKP、ΔKI、ΔKD也分成7个模糊区段{NB、NM、NS、ZO、PS、PM、PB}，其模糊论域为[-3,3]，也采用三角形隶属度函数如图4所示。

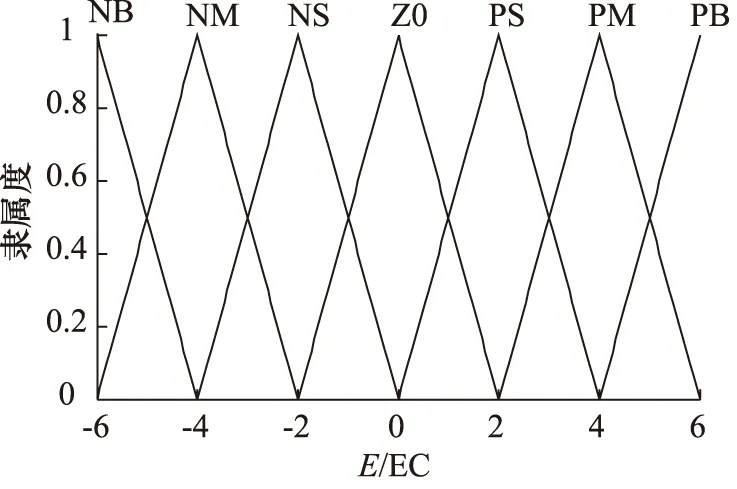
图3　E和EC的隶属度函数

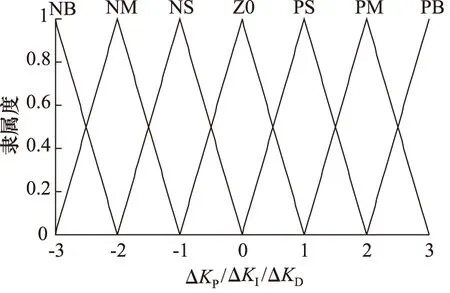
图4　ΔKP、ΔKI、ΔKD的隶属度函数

采用Mamdani模糊推理方法[9]，根据阀门位置的实际操控经验，将现场操作者在操作过程中可能遇到的各种情况和相应的控制策略汇总成表，制定控制规则。选取控制量的基本原则为：当误差大或者较大时以消除误差为主，当误差较小时以防止超调、稳定系统为主。KP越大系统响应速度越快，但过大会产生超调使系统不稳定；KI影响系统的稳态精度，越大则静态误差消除越快，但过大会使响应初期产生积分饱和现象从而增大超调；KD对系统动态特性影响较大， 过大会使响应过早提前制动以至于调节时间延长，过小会使响应曲线产生毛刺， 增加了执行机构不必要的调节浪费，对系统有害。因此，根据上述参数对系统输出特性的影响情况，归纳出了参数调整量ΔKP、ΔKI和ΔKD的模糊控制规则表如表1所示。

由表1可知，当误差E为负大、误差变化EC为负时，此时负误差有增大趋势，为尽快消除已有的负大误差，并抑制误差变大，应使控制量增加较快；当误差变化EC为正时，负误差有减小的趋势，控制量应取较小的值。当误差E为负中时，同误差为负大时类似，需尽快消除误差。当误差为负小时，系统接近稳态，微调即可。当误差为零时，看误差变化的大小微调控制量。当误差为正时，分析情况类似。需要指出的是，由专家经验获得的模糊规则在实际应用中对被控对象的控制效果可能并不是最好的，而且针对不同的调节阀控制对象其控制规则也不尽相同，这需要实际应用时随时调整其中的某些参量，直至达到最优控制效果。

采用重心法解模糊化[10]，得到KP、KI、KD的变化量后，计算应用于PID控制器的参数KP、KI、KD的公式为：

KP=KP0+ΔKP·qP

KI=KI0+ΔKI·qI

KD=KD0+ΔKD·qD

(11)

式中，qP，qI，qD是参数KP、KI、KD的调整因子，KP0，KI0，KD0是用常规PID整定法得到的整定值。

3　仿真研究

3.1　气动调节阀执行机构模型辨识

针对气动调节阀响应指令信号的变化时具有滞后和惯性的特点，建立了系统的二阶加纯滞后传递函数模型[11]：

(12)

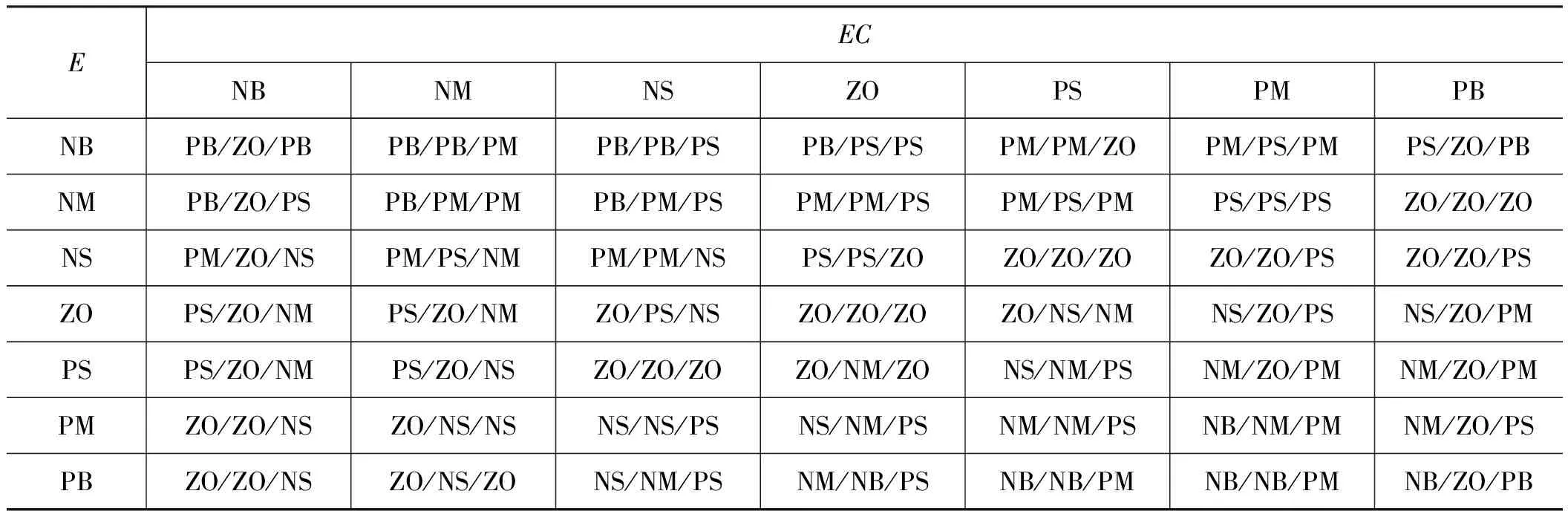
表1　ΔKP/ΔKI/ΔKD的模糊控制规则表

式中，U(S)为CPU输出的控制电压；Y(s)为执行结构位移输出量；m1、m2及n1、n2为待辨识参数。

采用最小二乘法对气动调节阀执行机构进行系统辨识，将上式转化为标准最小二乘法形式，其时域表述为：

m1u(t-δ)+m2u(t-δ)=

y(t)+n1y(t)+n2y(t)

(13)

假定u(t)为阶跃信号，幅值为A，将上式二次积分并化简为：

+0.5m2δ2)A+(m1-m2δ)tA+0.5m2t2A

(14)

将上式化为如下形式：

γ(t)=φΤ(t)θ

(15)

其中，θΤ=[n1,n2,-m1δ+0.5m2δ2,m1-m2δ,m2]。

由实际输入输出数据及最小二乘法求取向量θ的估计值，并设θi为估计量的第i个元素。最后得模型参数：

(16)

对调节阀定位系统进行采样实验，位置反馈单元测量一次输出位移量的时间间隔为Δt=0.02 s，采样数据达到稳态后停止采样，设总共选取的采样数据的长度为N=3600，截止时间tN约为72 s，系统延时0.1 s。最终得传递函数表达式为：

(17)

3.2　PID参数优化

为进行复合控制算法的仿真分析，首先应确定PID控制器的初始参数。本研究采用Signal Constraint模块[12]对PID参数进行优化，以获取普通PID控制的最优控制参数。参数寻优的约束条件设为：超调量≤20%，上升时间3 s，调节时间为20 s，误差范围±0.5%。分别采用梯度法、模式搜索法、简单搜索法三种算法进行了寻优试验，发现对于本系统模型采用模式搜索法的寻优效果最好，得到了如图5所示的PID参数优化效果曲线。寻优后获得的PID参数初值为：KP0=1.3288，KI0=0.1936，KD0=0.3361。

图5　signal constraint 模块对PID参数寻优效果图

3.3　仿真结果

在MATLAB/Simulink环境下进行仿真，以验证灰色预测模糊PID复合控制器的控制效果。采用S-Function 函数编写Grey prediction仿真模型，取建模维数m=5，预测步数h=3，采样周期设为2 s，每隔一个周期进行阀位当前值的数据采集、灰色预测和控制指令的求解。通常根据调节阀阀位目标值设定当前反馈值的控制范围，当灰色预测模型的预测输出值超出了该设定范围时，控制系统会及时调整执行机构的动作速度，使当前阀位变化量保持在规定的范围之内。模糊控制器使用fuzzy logic toolbox中的集成模块，按照第2.3节的理论输入相应隶属度函数和49条模糊控制规则并设置相关参数。模型搭建完成后进行仿真实验，系统仿真时间设为30 s。对比常规PID、模糊整定PID和灰色预测模糊整定PID控制器构成的系统的阶跃响应曲线，结果如图6所示。

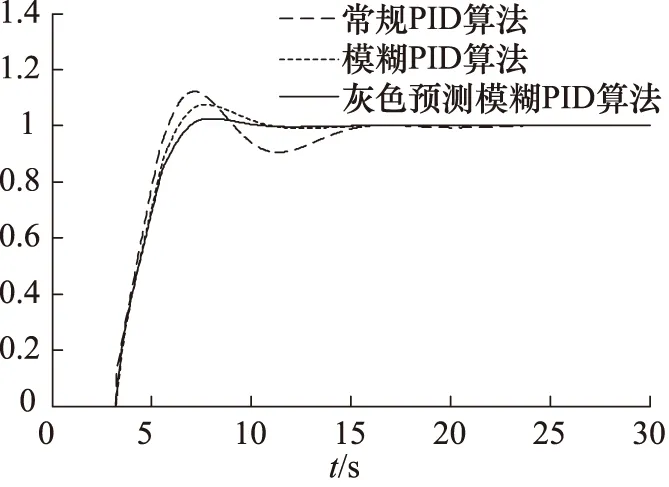
图6　系统阶跃响应曲线

由图6的响应曲线可得出表2所示的三种控制算法的性能指标对比：

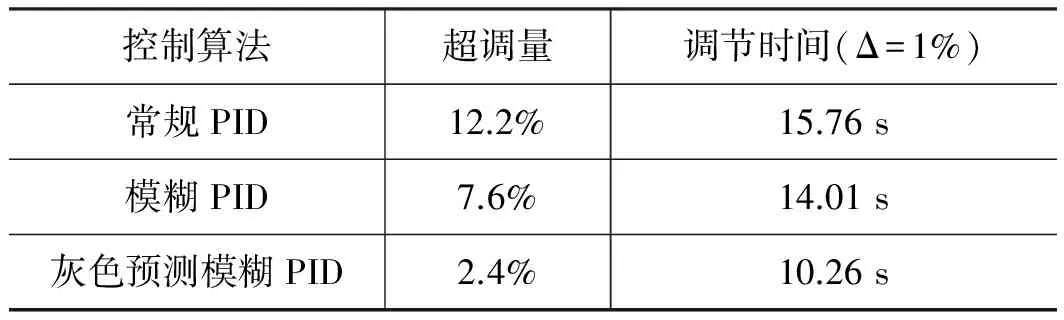
表2　系统阶跃响应性能指标

仿真结果表明： ① 常规PID算法的方式固定，参数不能根据外界环境的变化实时调整，故在此算法的控制作用下，系统超调量最大、调节时间最长、振荡最为明显，因此对于大惯性、纯滞后和时变性的气动调节阀系统，常规PID算法的控制效果不理想，且抗干扰能力较差；② 在常规算法中加入模糊环节后，因模糊PID算法能够在线调节控制参数，故在一定程度上提高了响应速度，降低了超调量和调节时间，系统振荡情况得到改善。但是，模糊PID算法的滞后特性使得系统误差不能及时消除，属于“事后控制”，系统响应仍存在较大超调，且需花费较长调节时间，对于要求高精度和高速度的气动调节阀系统，还需效率更高的控制算法；③ 灰色预测模糊PID算法中，灰色预测模型可将系统不确定部分进行粗略估计，并对不确定部分及外界未知干扰实施一定补偿，属于“超前控制”，可以很好的解决调节阀定位系统的滞后性问题，且系统每采样一个阀位输出值就能建立一个新的模型，增强了系统的自适应能力，故该算法在仿真实验中系统的响应性能最为出色。灰色预测模糊PID算法结合了常规PID，模糊环节和灰色预测模型的优势，实现对控制参数的高效在线整定，其算法计算量较小，实时性也很好，增强了系统的整体控制效果。

由于工业控制现场的调节阀种类、参数各异，不同的气动调节阀其系统模型也不尽相同，若将控制系统按流量、温度和压力等参数来分类，属于同一类别的系统，其对象特性往往比较接近，故采用的控制器形式和整定的参数均可互相参考。系统控制规律的选择主要有下面几种情况： ① 对于一阶惯性加纯滞后对象，如果负荷变化不大，控制要求精度较高，工艺要求不高，可采用PI控制；② 对于纯滞后时间较大，负荷变化也较大，控制性能要求较高的场合， 可采用PID控制； ③ 对于高阶惯性环节加纯滞后对象，负荷变化较大，控制性能要求很高时，需采用复合控制算法，如模糊PID、灰度模糊PID等高精度控制算法。本研究的灰色预测模糊复合控制算法可以满足阀位智能调节控制系统对阀门定位的实时性和精度的要求。仿真结果表明，该算法响应速度快、超调小、调节精度高、稳态性能好，其调控性能优于常规PID控制和模糊整定PID控制。

4　结论

(1) 针对惯性、时滞的气动调节阀建立了二阶加纯滞后仿真模型，采用最小二乘法进行参数辨识，对调节阀系统进行了采样实验，获得了仿真所用的调节阀执行机构模型的传递函数；

(2) PID控制器初始参数的确定是系统进行仿真实验的关键，本研究采用Simulink最优化软件包中的Signal Constraint模块对普通PID的控制进行了参数寻优，限定了系统阶跃响应的相关条件，获取了较为合理的参数；

(3) 灰色预测的“超前控制”作用可以很好的解决调节阀定位系统的滞后性问题，与模糊控制算法的结合可以实现对PID参数的在线整定，其调控性能超越了常规的两种控制算法。

参考文献：

[1]冯卫星,樊泽明,王亮.智能阀门定位器PID参数自整定及控制算法设计[J].机床与液压,2009,37(11):143-144.

[2]刘娜,何永勃,苏兴国.基于预估模糊自适应PID控制的智能电气阀门定位器的应用研究[J].自动化与仪器仪表,2010,(4):66-67.

[3]Ranjbari L,Shirdel A,Aslahi-Shahri M,et al.Designing Precision Fuzzy Controller for Load Swing of User Overhead Crane [J].Neural Computing & Applications,2015,(26): 1-6.

[4]LUO Y, ChE X, HE Z, et al. Grey Self Adaptive Fuzzy Sliding Mode Control for Flight Simulator Servo System[J]. Lecture Notes in Computer Science,2008:265-274.

[5]王耀南.智能控制系统[M].长沙:湖南大学出版社,2006.

[6]卢懿.灰色预测模型的研究及其应用[D].杭州：浙江理工大学,2014.

[7]李战明,张永江.基于计算型模糊推理算法的模糊控制器设计[J].计算机工程与应用,2014,50(14):259-264.

[8]Sie W, Lin R L B. Enhancing Grey Prediction Fuzzy Controller for Active Suspension Systems [J]. Vehicle System Dynamics International Journal of Vehicle Mechanics & Mobility, 2006, 44(5):407-423.

[9]M Lee W, S Liao Y. Adaptive Control of the Wedm Process Using a Self-Tuning Fuzzy Logic Algorithm with Grey Prediction [J]. International Journal of Advanced Manufacturing Technology, 2007, 34(5-6):527-537.

[10]陈磊,暨仲明.基于气动调节阀的一体化智能测控装置与应用[J].杭州电子科技大学学报,2014,34(3):103-106.

[11]周欢喜.气动智能阀门定位器设计与实现[D].南京：南京理工大学,2014.

[12]刘文定,王东林.MATLAB/Simulink与过程控制系统[M].北京:机械工业出版社,2012.