基于CFD技术的特高压断路器液压缸缓冲特性研究

　， ， 　， 小勇

(武汉大学 动力与机械学院， 湖北 武汉　430072)

引言

本研究对象是特高压断路器液压缸。特高压断路器是特高压输电系统的核心部件[1]。在断路器分合闸过程中，由于液压操动机构具有高速度大能量，且要求高稳定性和低故障率，同时液压缸内部流场的压力达到100 MPa以上，如果不对其进行适当缓冲，会导致系统不稳定，产生很大的噪声，甚至可能损坏液压缸及其他液压元件[2-4]。对于断路器液压缸缓冲特性的研究，国外开展的较早，Murali和Beegamudre[5]于1979年建立了液压缸缓冲的数学模型，并对缓冲过程进行流体动力学分析。国内则侧重于对缓冲装置的研究，丁凡[6]研究了采用短笛型缓冲装置的高速液压缸缓冲过程，介绍其理论及试验结果。刘伟[7]等建立了控制阀及液压缸的仿真模型，并对断路器分合闸特性进行仿真分析，同时通过试验测试液压缸油压以及位移速度等特性。邹高鹏[8]等分析了阶梯型柱塞的缓冲机理，借助AMESim对关键参数进行变参分析。孟尧[9]等提出使用MATLAB对缓冲过程进行仿真，分析了缓冲装置的各个参数对缓冲效果的影响。影响液压缸缓冲效果的因素较多，本研究着重研究油液过流面积、柱塞运动速度以及油液属性对缓冲特性的影响。

本研究采用CFD流场分析法研究特高压断路器液压缸的缓冲特性，运用动网格技术准确地模拟液压缸内部流场形态，得到压力分布和速度分布，并通过改变液压油的体积弹性模量、黏度和密度来研究油液属性对缓冲特性的影响。

1　缓冲过程及几何模型

1.1　缓冲过程分析

如图1所示，在缓冲过程中柱塞向右运动，同时推动液压油进入节流孔。根据过流面积的变化情况，可将缓冲过程分为圆面节流、锥面节流和环面节流三个阶段。

图1　柱塞运动示意图

在圆面节流阶段，缓冲柱塞离节流孔较远，油液的流动是由节流孔处的圆面来限制的。由于该阶段油液的过流面积较大，因此缓冲效果不明显。

在锥面节流阶段，柱塞的前端与节流孔形成一个圆台，油液的过流面为锥面。由公式(1)：

(1)

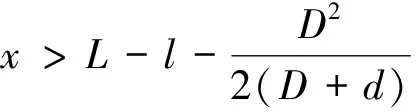
由于该阶段油液的过流面积随着柱塞的移动而逐渐减小，从而导致油腔压力逐渐升高，具有一定的缓冲效果。

在环面节流阶段，柱塞进入节流孔，油液的过流面为两者之间形成的环面，由于该阶段过流面积最小，因此油腔压力较大，缓冲效果明显，但过高的油压也会影响系统的稳定性。

1.2　几何模型

本研究中的特高压断路器液压缸的缓冲柱塞为台阶形，模型结构如图2所示。

图2　九级台阶模型结构示意图

柱塞的最小直径dmin=52.6 mm，最大直径dmax=54.8 mm，其余尺寸为D=55 mm，l=85 mm，L=230 mm。 由于液压缸是回转体，可将图2中心线上半部分的流场区域作为计算域，即对模型进行适当简化，在受到计算机硬件条件限制以及保证计算精度的前提下，以二维模型代替三维模型进行计算。将两个圆形出口改为环形出口，经过多次计算已验证该简化对计算结果基本无影响。

2　数值模拟

2.1　基本方程

流体流动所遵循的物理定律是建立流体运动基本方程的依据。质量守恒、动量守恒和能量守恒控制方程的通用形式如下[10]：

(2)

式中，u为速度矢量；t为时间；φ为通用变量，代表u，v，w和T等求解变量；Γ为广义扩散系数；S为广义源项。

2.2　湍流模型

由于液压缸活塞杆的高速运动以及内部流道结构的不规则，使得液压缸内流场相当复杂。该流场的最小雷诺数可认为是在排油腔位置。由雷诺数计算公式Re=ρ·U·L·u-1可知当其大于临界雷诺数Rec(2000)时，特征速度U>0.6667 m/s，根据实际情况可知在液压缸的工作过程中，内部流体的流动状态主要是湍流，可以用k-ε湍流模型对其进行计算。

k-ε湍流模型引入了湍流黏度系数μt，它是湍动能k和耗散率ε的函数[11]，即：

(3)

标准k-ε湍流模型的k和ε方程形式如下：

(4)

(5)

式中，Gk表示由于平均速度梯度引起的湍动能产生；Gb表示由于浮力影响引起的湍动能产生；YM表示可压缩湍流脉动膨胀对总的耗散率的影响。附加的经验常数如下：C1z=1.44；C2z=1.92；C3z=0.09，湍动能k和耗散率的湍流普朗特系数分别为σk=1.0，σz=1.3。

2.3　网格及边界条件

由于每个时间步的计算域都不相同，本研究采用动网格瞬态计算方法。如图3所示，缓冲柱塞作为运动边界，当其进入节流孔后，两者的最小间隙为0.1 mm，为了保证仿真的精度，将节流孔附近分割出的一个面划分为8层四边形结构化网格，该部分网格在仿真过程中不参与网格重生，其余部分为三角形网格。本模型在初始时刻共有117617个网格单元，其中有112个结构化四边形网格。通过编写profile文件将速度赋予该模型的运动边界，时间步长由网格尺寸以及柱塞瞬时速度来确定。出口采用压力出口边界条件，液压缸内壁为绝热无滑移的静止壁面，近壁面采用标准壁面函数，通过多次仿真发现采用Coupled算法最易收敛。

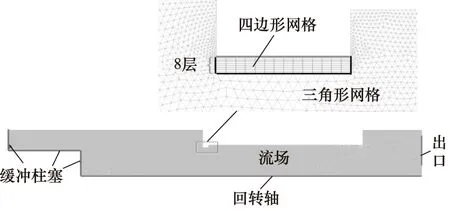
图3　流场网格

由于工作时长只有几十毫秒，因此假设系统的温度在该过程中保持不变。将液压油作为黏性可压缩流体进行计算，其体积弹性模量为2 GPa，动力黏度值为17 cp。

3　数值模拟结果与分析

通过数值计算得到液压缸流场的压力云图和速度矢量图以及流场压力值。

缓冲过程中每个时间步流场最大压力的变化如图4中的压力曲线所示，柱塞的运动速度如图4中的速度曲线所示。从图中可以看出：压力值在初始阶段较小且基本无波动，同时柱塞的速度逐渐增大；在柱塞接近节流孔时压力值迅速增加，到达峰值后再逐渐减小并有明显的波动，在该过程中柱塞的运动速度迅速下降。

图4　流场压力与柱塞速度变化曲线

在柱塞运动过程中流场的压力主要是受过流面积的影响。当柱塞离节流孔较远时，流场处于圆面节流阶段，过流面积为2375.8 mm2，此时流场压力对柱塞的缓冲作用较小，因此柱塞运动速度逐渐增大。

当缓冲柱塞靠近节流孔时，流场从圆面节流进入锥面节流阶段，根据公式(1)可得此时柱塞位移x=130.9 mm，此后流场压力迅速增大，对柱塞具有较大的缓冲作用，柱塞的运动速度开始下降。当柱塞的位移为x=145 mm时，流场进入环面节流阶段，在x=157.7 mm处压力达到最大值。由于每级台阶的直径不同，过流面积也在变化。环面节流阶段油液过流面积最大为202.8 mm2，最小为17.3 mm2。通过对比可发现，圆面节流阶段的油液过流面积远大于环面节流阶段。

分析其原因，当柱塞进入到锥面节流阶段，油液过流面积随着柱塞移动不断减小，会对无杆腔的油液造成“挤压”，由图4可知此时的柱塞运动速度较大，在较小的过流面积和较大的运动速度的共同作用下，无杆腔油压迅速增大。如图5所示为锥面节流阶段的流场形态，此时柱塞位移为140.42 mm。无杆腔内压力分布较为均匀，几乎都达到了最大值，因此可以用流场的最大压力值近似表示无杆腔的压力。由图5中的局部压力云图和速度矢量图可知，节流锥面已经形成，无杆腔内的高压油通过节流锥面，压力逐渐降低，过渡到排油腔内的低压油，油液速度方向垂直于节流锥面。

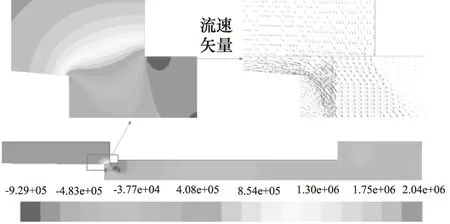
图5　位移x=140.42 mm流场形态

由于环面节流阶段油液的过流面积远小于圆面节流阶段，因此压力值较大。但由于此阶段柱塞的运动速度也在逐渐减小，所以压力的整体趋势是减小的。如图6所示，此时第二级台阶位于节流孔中，可以从图中看出节流环面的存在。

图6　位移x=164.09 mm节流孔附近局部流场形态

在下一级台阶进入节流孔前的一段时间内，节流形式会从环面节流变为锥面节流，由图4可知该阶段压力剧烈波动。如图7所示，此时柱塞的位移为173.84 mm，第二级台阶即将进入节流孔，对比图6可以看出第二级台阶与节流孔形成节流锥面，在柱塞的这一小段位移内，节流面积逐渐减小，压力上升。不难得出在每级台阶进入节流孔前，两者之间会形成节流锥面，进入节流孔后就形成节流环面。环面节流与锥面节流阶段交替出现，在最后一级台阶进入节流孔后，流场保持环面节流直至行程末端。而在柱塞的最后一级台阶进入节流孔后，因过流面积过小导致压力剧增。

图7　位移x=173.84 mm节流孔附近流场形态

4　变参分析

液压油的属性主要有密度、黏度、体积弹性模量等，液压油质量的优劣直接影响液压系统的工作性能[12]。

4.1　体积弹性模量的影响

为了研究油液的体积弹性模量对缓冲特性的影响，在其他参数不变的情况下，体积弹性模量分别取为2 GPa，1.5 GPa，1 GPa，计算结果如图8所示。

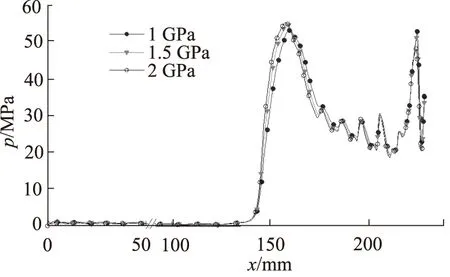
图8　不同体积弹性模量的压力曲线

图8中各结果曲线的趋势基本一致，在柱塞进入节流孔之前，流场压力较小，各曲线基本重合。当柱塞进入节流孔后， 各曲线出现差异。 体积弹性模量为2 GPa 的油液峰值压力为55.32 MPa，其对应的位置为157.7 mm；体积弹性模量为1.5 GPa的油液峰值压力为54.86 MPa，其对应的位置为158.4 mm；体积弹性模量为1 GPa的油液峰值压力为53.28 MPa，其对应的位置为159.3 mm。由此可知，液压油的体积弹性模量越大，流场出现峰值压力的位置就越靠前，峰值压力也越大。在柱塞运动后期，各压力曲线基本重合。油液的体积弹性模量越大，则其“弹性”越小，传动刚度越大[13]。因此在柱塞进入节流孔后其流场压力也越大，缓冲效果也越明显。

4.2　黏度的影响

为了研究液压油的黏度对缓冲特性的影响，现取其在常压下0，20 ℃以及40 ℃时的动力黏度值30 cP， 17 cP和10 cP分别计算，结果如图9所示。

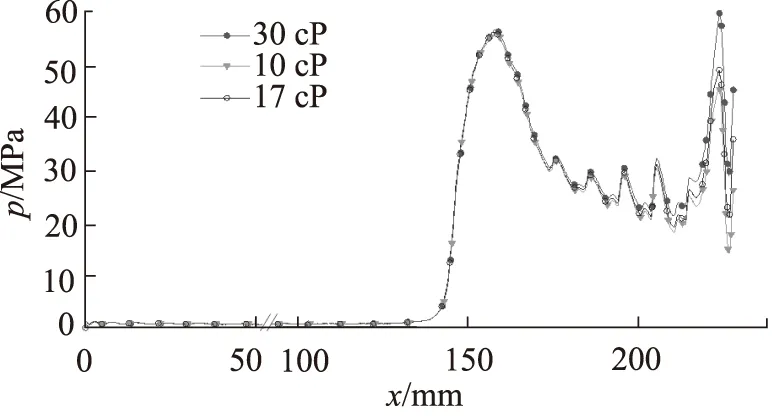
图9　不同黏度的压力曲线

由图9可知，在柱塞运动的初始阶段各压力曲线基本重合。从位移x=153 mm开始，各曲线出现较明显的差异，此时第二级台阶已进入节流孔，此后黏度为30 cP的油液压力最大，黏度为10 cP的油液压力最小。因此可知，当液压油的过流面积较大时，黏度对流场压力的影响较小，而当过流面积较小时，黏度会对流场压力产生较大影响。油液黏度越大，其分子之间的内摩擦力也越大，油液的流动受阻[14]。当过流面积较大时这种现象并不明显，但当缓冲柱塞与节流孔的间隙较小时，油液流动受阻明显。因此在柱塞运动后期，黏度值越大的油液缓冲压力也越大，波动也越剧烈，易造成液压系统不稳定。

4.3　密度的影响

为了研究油液的密度对缓冲特性的影响，现分别将常温常压下的油液密度取为800 kg/m3、850 kg/m3、900 kg/m3进行计算，结果如图10所示。

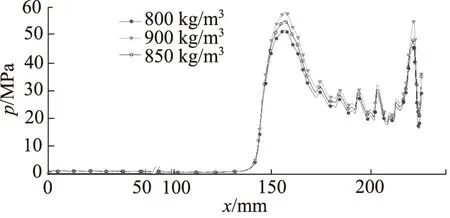
图10　不同密度的压力曲线

从位移x=146.5 mm开始，各压力曲线出现明显分离，此时柱塞的第一级台阶已有部分进入节流孔。此后，密度为900 kg/m3的油液压力最大，密度为800 kg/m3的油液压力最小，各曲线变化趋势相同。由此可知，当油液过流面积较大时，密度对压力的影响基本可忽略，而当油液的过流面积较小时，密度会对压力产生较大影响。油液的密度越大则其单位体积的质量也越大，从而使推动油液前进所需的力较大，导致油液的压力也越大[15]。当过流面积较小时该现象明显，其对柱塞的缓冲效果也越好，但过高的油压会导致系统不稳定。

5　结论

(1) 以柱塞形状为台阶形的特高压断路器液压缸为研究对象，采用CFD动网格技术对缓冲过程中的流场进行数值模拟；

(2) 在缓冲过程中，流场压力主要受过流面积的影响。在柱塞运动的初始阶段，流场压力较小且趋势平稳。从第一个锥面节流阶段开始，油液压力急剧上升，并在第二级台阶位于节流孔中时出现最大值。此后油液压力的整体趋势是减小的，而由于节流锥面的存在，在每级台阶靠近节流孔时压力值都会出现波动；

(3) 通过对液压油属性进行变参分析得到如下规律：液压油的体积弹性模量越大，流场出现峰值压力时柱塞的位移就越小，峰值压力也越大；当过流面积较小时，油液黏度或密度越大，缓冲压力也越大，且波动越剧烈。在实际的工程应用以及研究中应考虑液压油属性对缓冲特性的影响。

参考文献：

[1]孙艳玲，王永良，雷琴，李铁．特高压断路器液压操动机构仿真研究[J]．高压电器，2014，50(10)：10-19．

[2]伍中宇.超高压断路器液压操动机构特性研究[D]．杭州：浙江大学，2008．

[3]Wei Liu， Bing Xu， HuaYong Yang， HongFei Zhao， JunHui Wu．Hydraulic Operating Mechanisms for High Voltage Circuit Breakers: Progress Evolution and Future Trends[J]. Science China Technological Sciences，2011，54(1)：116-125．

[4]丁孺琦，徐兵，刘伟，王永良.百万伏大功率操动机构液压系统优化设计[J]．液压气动与密封,2012(9)：4-8．

[5]Murali，Beegamudre N．Analysis of Hydraulic Cylinder Cushioning[J]．Hydraulics & Pneumatics，1979，32(5)：72-75．

[6]丁凡．短笛型缓冲结构的高速液压缸缓冲过程的研究[J]．中国机械工程，1998，9(10)：51-54．

[7]刘伟，徐兵，杨华勇，伍中宇．高压断路器液压操动机构特性分析[J]．中国机械工程学报，2010，46(10)：148-155．

[8]邹高鹏，王永良．高压断路器配液压操动机构液压缸缓冲特性的仿真研究[J]．液压与气动，2011,(9)：73-75．

[9]孟尧，刘忠，李晶晶．基于MATLAB的沟槽型节流缓冲装置仿真与分析[J]．机床与液压，2014，42(5)：132-135．

[10]孙露，谷正气，杨易，杨滨徽，龚旭．轿车与卡车超车过程中瞬态气动特性分析[J]．中南大学学报，2011，42(9)：2681-2686．

[11]张淑佳，李贤华，朱保林，胡清波．k-ε涡黏湍流模型用于离心泵数值模拟的适用性[J]．机械工程学报，2009，45(4)：238-242．

[12]时培成，王幼民，王立涛．液压油液数字建模与仿真[J]．农业机械学报，2007，38(12)：148-151．

[13]岳国良，李楠．航空液压油体积弹性模量的测定方法[J]．合成润滑材料，2011，38(1)：19-21．

[14]朱仁宗，杜彦亭，金明哲．液压油黏度对超高压系统的影响[J]．机床与液压，2003(4)：249-250．

[15]闫清东，李晋，魏巍．工作油液温度对液力变矩器性能影响计算流体力学分析及试验研究[J]．机械工程学报，2014，50(12)：118-12．