8 MN液压机电液比例控制系统的仿真分析

， ，

(四川大学 制造科学与工程学院， 四川 成都 610065)

引言

8 MN双动拉伸液压机的液压系统由使工件成形的拉伸滑块系统、防止工件折皱的压边系统、配合压机单动的模具缓冲垫系统、工作台移动系统、控制这些系统工作的辅助控制系统五个基本单元构成，并且把比例电磁阀应用在液压系统中较为重要的拉伸滑块系统、压边滑块系统和模具缓冲垫系统。运用电液比例阀能够实现压力、流量、方向的连续变化方便地实现机电液一体化控制，用于液压机液压系统中，可以有效地提高液压机的性能[1,2]。

为了掌握8 MN液压机电液比例控制系统的工作特性和相关参数的变化，以便进一步对该系统进行改进和完善，达到提高液压系统的可靠性、控制精度和响应特性的目的，对液压系统进行了计算机仿真分析。

1 建立液压控制系统的模型

建立液压系统的数学模型通常有两种途径：理论法和实验法[3]。采用理论法对液压系统的元件构成进行分析，通过推导建立压力控制系统和速度控制系统的两种框图模型，分别如图1和图2所示。

2 液压机电液比例系统控制策略分析

研究表明模糊自适应PID控制简单、方便，使控制系统具有良好的动态和稳态特性。模糊自适应PID控制器由模糊推理和参数可变PID控制构成。其原理如图3所示。

模糊控制器首先对输入量进行模糊化， 转换成模糊论域中的模糊变量，然后根据模糊规则进行模糊推理，得到模糊控制量，再对模糊控制量进行解模糊，最后输出PID控制器Kp、Ki、Kd三个参数的变化量。模糊自适应PID控制器运行时不断检测e和ec，然后根据模糊控制规则对PID的三个参数实时修改，以实现不同状态下控制系统仍具有良好的动态和稳态特性。

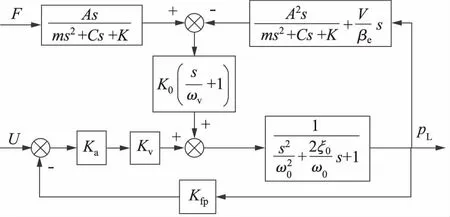
图1 压力控制系统框图模型

图2 比例速度控制系统框图模型

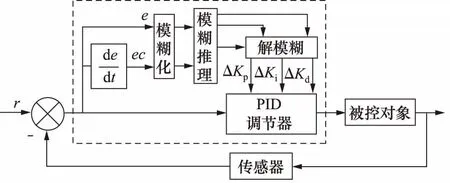
图3 模糊自适应PID控制结构图

1) 输入输出变量

模糊自适应PID控制器采用两输入、三输出的控制器。以控制系统的误差e和误差变化率ec为输入；以PID控制器三个参数Kp、Ki、Kd的增量ΔKp、ΔKi、ΔKd为输出。

2) 模糊化

为了完成模糊推理计算，需将精确量进行模糊化。模糊论域一般表示为：[-N，-N+1，…，0，…，N-1，N]，其中N为整数。模糊子集通常选择七个语言词的集合，表示为：{ NB，NM，NS，ZO，PS，PM，PB }，分别代表负大，负中，负小，零，正小，正中，正大。输入变量的模糊论域一般取N≥6，输出变量的模糊论域一般取N≥7。这样能满足模糊集论域中所含元素个数为模糊语言集总数的2倍以上，保证各个模糊集合能较好地覆盖论域，避免出现失控现象[4]。

在实际的控制系统中，输入变量的基本论域的范围与其模糊论域的范围并不一致，这时需要通过量化因子进行论域间的转换，量化因子定义为：

(1)

式中，emax为误差e基本论域中的最大值；ecmax为误差差变化率ec基本论域中的最大值。同样，输出的模糊控制量的模糊论域与其基本论域也会不一致，需要乘以一个比例因子将其转换到基本论域中去，比例因子定义为：

(2)

式中，umax为输出变量基本论域的最大值。

模糊语言值最终通过隶属函数来描述。工程应用中为了减小计算量，常常使用占用内存较小的三角形和高斯型隶属函数。当系统偏差和系统偏差变化率比较小的时候，采用分辨率极强的三角形隶属函数，当偏差和偏差变化率较大的时候，通常采用高斯型隶属函数[5]。

3) 模糊控制规则

模糊自适应PID控制的核心就是建立三个输出控制量ΔKp、ΔKi和ΔKd与输入量e和ec之间的模糊关系，使系统在不同的状态下仍然具有很好的动态、静态性能。根据Kp、Ki和Kd对系统的调节作用，可以建立起模糊控制规则表，如表1～表3所示[6]。

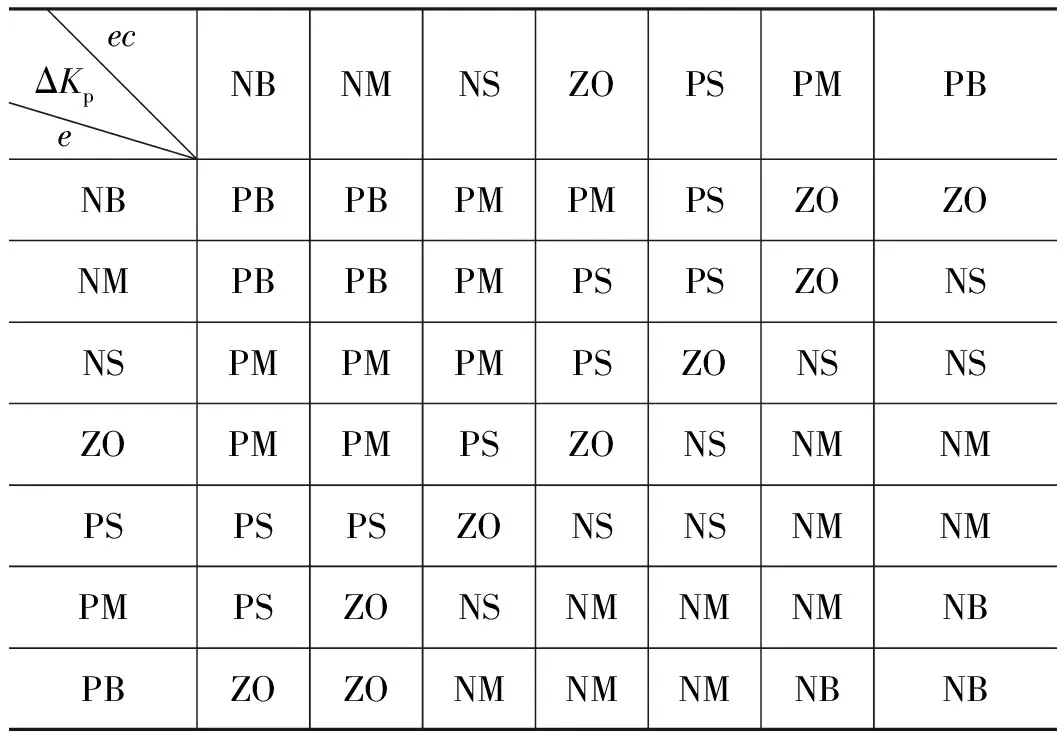
表1 ΔKP模糊控制规则表

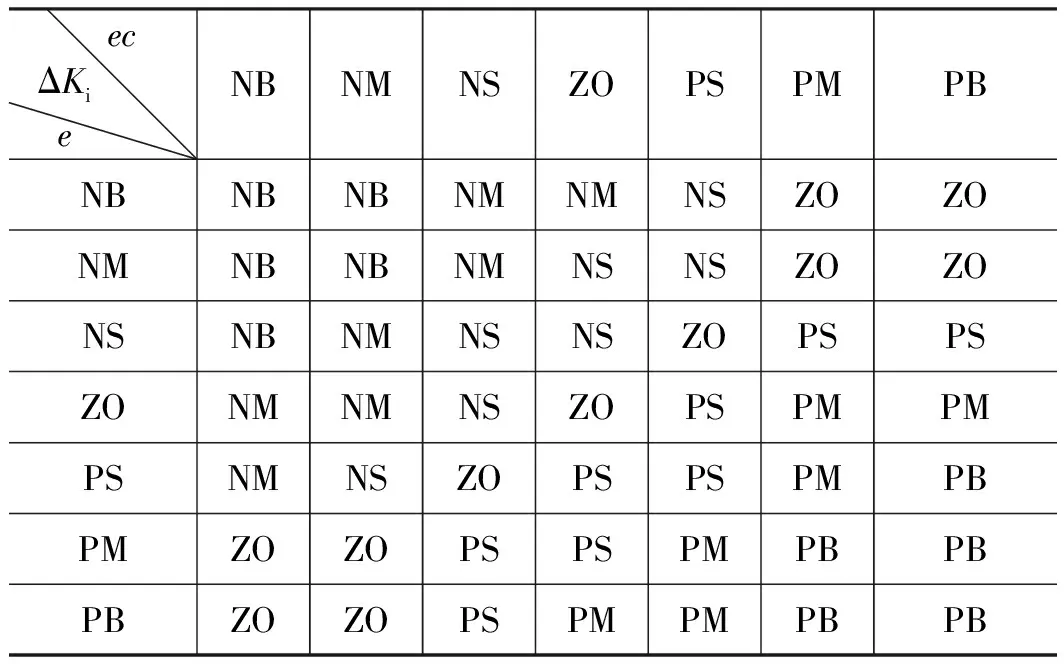
表2 ΔKi模糊控制规则表

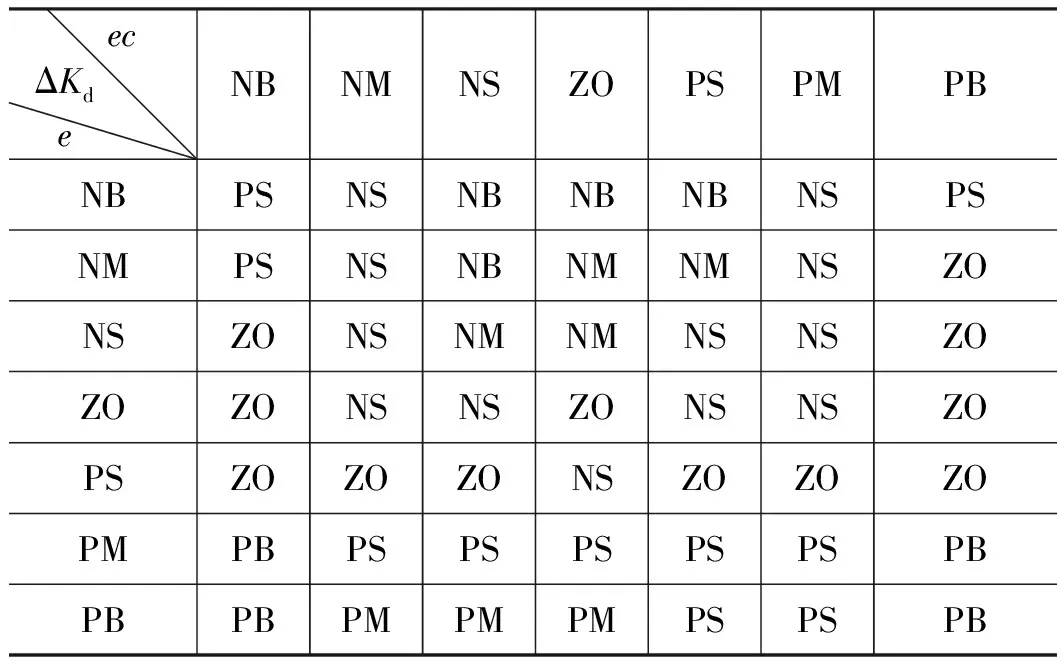
表3 ΔKd模糊控制规则表

模糊自适应PID控制器是个2输入3输出的控制系统，总共有49条模糊控制规则，把这些规则写成如下启发式语句：

if (eis NB) and (ecis NB) then (ΔKpis NB), (ΔKiis NB),(ΔKpis PS)

采用工程中常用的Mamdani模糊推理法，它可以实现具有多个前件多条规则的推理，能够满足要求。

4) 解模糊

常用的解模糊的方法有最大隶属度法、加权平均法、取中位数法。加权平均法全面考虑模糊控制量的相关信息，并且运算简单本研究采用此种方法。

3 液压系统仿真分析

基于机理建模法建立了系统的数学模型，采用MATLAB对控制系统进行仿真分析。

3.1 模糊自适应PID控制器设计

首先根据各液压元器件的自身特性尺寸，来计算出元件各自的相关参数，其中包括液压缸，比例溢流阀以及比例方向阀等。通过两种阀来确定出压力传感器和速度传感器的增益。根据这些参数，利用MATLAB中的模糊逻辑工具箱对模糊控制器进行设计。模糊自适应PID控制器为2输入(e,ec)、3输出(ΔKp、ΔKi、ΔKd)的控制器。比例阀的输入电压为-10 V～10 V，因此，偏差e和偏差变化率ec的基本论域分别为：e[-10,10]，ec[-30,30]；输入量的模糊论域都为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}。输出量ΔKp、ΔKi、ΔKd的基本论域分别为：ΔKp[-4,4]，ΔKi[-10,10]，ΔKd[-0.2,0.2]，输出量的模糊论域都为{-8，-7，-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6，7，8}。则量化因子和比例因子计算如下：Ke=0.6，Kec=0.2，Kup=0.5，Kui=1.25，Kud=0.025。

在MATLAB模糊管理编辑器中编辑输入输出量的隶属度函数。输入量的隶属度函数，中间部分使用分辨率极强的三角型函数模糊化，边缘部分采用分辨率稍弱的高斯型函数模糊化。偏差e和偏差变化率ec隶属度函数相同，三个输出量全部采用三角型函数模糊化。再将表1～表3中的模糊控制规则输入到编辑器中[7]。

3.2 比例压力控制系统仿真分析[8]

在MATLAB的Simulink仿真环境中建立液压机比例压力控制系统的仿真模型。分别建立未加控制策略的系统仿真模型和添加模糊自适应PID控制策略模型。初步确定三个参数的初始值为：Kp0=0.8，Ki0=12，Kd0=0.04。输入电压设置为5 V，仿真时间设置为2 s，未加控制器时的响应曲线如图4虚线所示。

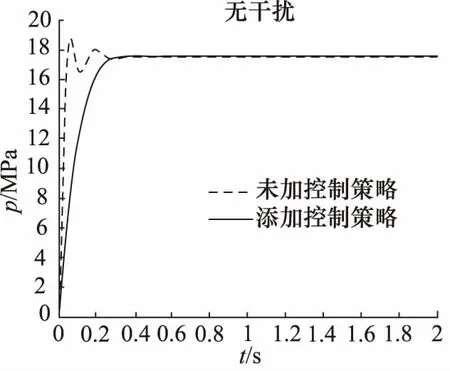
图4 压力控制系统无干扰响应曲线

经过分析，比例压力控制系统的最大输出压力为18.8 MPa，稳态输出压力为17.5 MPa，最大超调量为7.43%，上升时间约为0.04 s，调整时间约为0.4 s。系统调整时间长，稳定时有较大的振荡。

加入模糊自适应PID控制器之后的阶跃响应曲线如图4实线所示。此时当输入电压为5 V时，输出的最大压力为17.62 MPa，稳态输出压力为17.56 MPa，最大超调量为0.342%，调整时间约为0.28 s。加入模糊自适应PID控制后，系统达到稳态的过程无振荡出现，调整时间缩短。

系统在负载干扰作用下的响应曲线如图5所示，扰动F设为1 MN。未加控制策略时系统扰动较大，最大压力为19 MPa，压力变化18.57%，调整时间约为0.55 s。在模糊自适应PID控制策略下，系统最大输出压力18.1 MPa，压力变化3.43%，调整时间约为0.3 s。系统加入了模糊自适应PID控制后稳定性提高，响应更加迅速

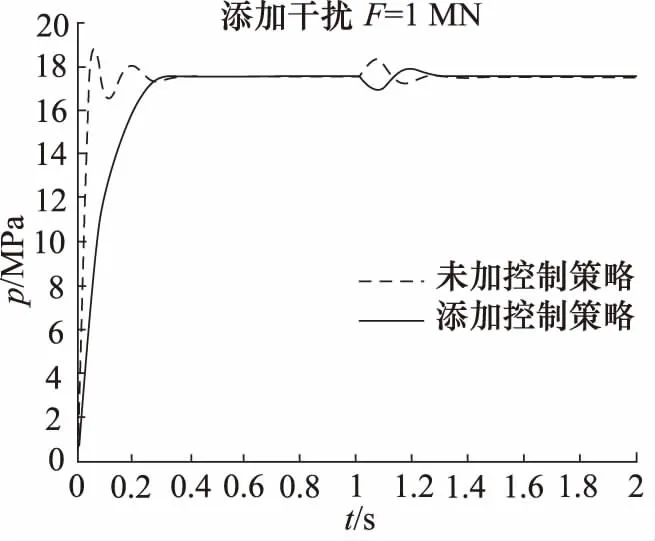
图5 压力控制系统干扰响应曲线

3.3 比例速度控制系统仿真分析

仿真模型中输入的电压5 V，仿真时间设置为2 s。模糊自适应PID控制器中三个参数的初始值确定方法同压力控制系统一样。在MATLAB中求得三个参数的初始值：Kp0=4.8，Ki0=160，Kd0=0.36，带入相关数据后，系统的阶跃响应如图6。未加控制策略时，最大输出速度为23.2 mm/s，稳态输出速度为16.6 mm/s。最大超调量39.76%，上升时间约为0.068 s，调整时间约为0.6 s。系统调整时间较长，达到稳定时有较大的振荡；添加模糊自适应PID控制策略后，速度控制系统最大输出速度为17 mm/s，稳态速度为16.6 mm/s，最大超调量为2%。上升时间约为0.15 s，调整时间约为0.28 s。达到稳态过程不会出现较大的振荡。

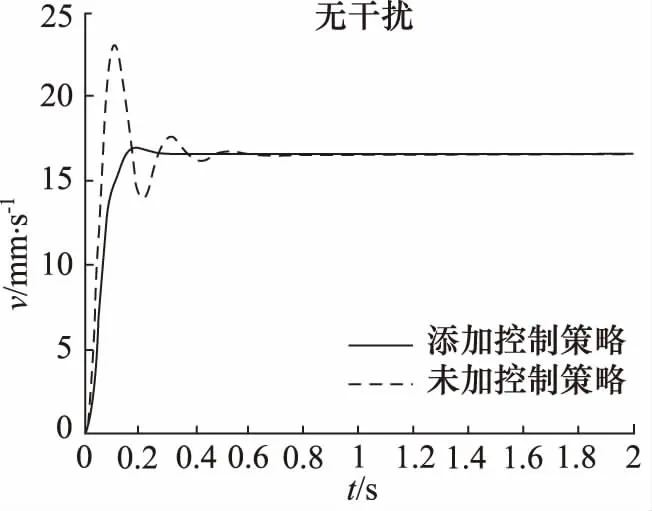
图6 速度控制系统无干扰响应曲线

运行过程中，将扰动力设为8 MN，观察系统的响应曲线。如图7所示，在外界干扰作用下，未加控制策略时系统速度有较大的波动，最小速度14.4 mm/s，稳态时速度为15.2 mm/s，速度波动为13.25%，稳态速度变化为8.43%；系统加入模糊自适应PID控制策略后，干扰作用下速度几乎没有出现波动，最小速度为16.4 mm/s，速度波动1%。稳态速度没有发生较大变化。加入控制策略之后，系统抗干扰能力强。

图7 速度控制系统干扰响应曲线

4 结论

根据理论建模方法建立了液压机比例压力控制系统和比例速度控制系统的数学模型。通过对不同控制策略的分析与研究，确定采用模糊自适应PID控制策略对液压机比例压力和比例速度控制系统进行改进，以提高系统的动态响应特性。

利用MATLAB中的Simulink环境建立系统的仿真模型，分析系统在不同工作状态下的响应曲线。根据仿真的响应曲线得出模糊自适应PID控制策略能够有效的改善系统的动态特性。

参考文献：

[1] 牛占海，王宏武，刘榛.对电液比例控制系统的综述[J]. 机械研究与应用，2004,17(6)：16-17.

[2] 许益民. 电液比例控制系统分析与设计[M]. 北京：机械工业出版社，2005.

[3] 伍洪云，陈飞，黄飞.电液比例溢流阀动态性能的实验研究[J].液压与气动，2009,(6)：72-74.

[4] 曹春平，孙宇. 液压机压边力模糊PID智能控制系统研究[J]. 中国机械工程，2010,21(21):2551-2554.

[5] 强宝民，刘保杰. 电液比例位置控制系统的新型PID控制算法研究[J].液压与气动，2012,(2):15-18.

[6] 陈晓冲，王万平. 常规PID控制和模糊自适应PID 控制仿真研究[J]. 机床与液压，2004,(12):65-66.

[7] Karam M. Elbayomy et al. PID Controller Optimization by GA and Its Performances on the Electro-hydraulic Servo Control System[J]. Chinese Journal of Aeronautics,2008,(21):378-384.

[8] 杨益兴.模糊自适应PID 控制器及Simulink仿真实现[J]. 舰船电子工程，2010，30(4):127-130.