电液加载系统的多余力抑制方法

,

(北京航空航天大学 自动化科学与电气工程学院, 北京 100191)

引言

加载系统是一种力(力矩)伺服系统，有主动式和被动式加载两种方式。被动式加载系统属于位置扰动型施力系统[1]，其特点是对运动的被加载对象施加负载。通过加载系统可以在实验台上模拟载荷谱，以检验被试验设备的带载性能。

从第一台电液负载模拟器原理样机[2]诞生至今，加载系统的应用从航空航天领域的舵机和作动器系统加载，扩展到了舰船减摇鳍系统的加载[3]、海洋拖曳系统加载[4]、运输工具的路况和负载的模拟[5]、车辆和发动机加载[6]等领域，还衍生出了飞行模拟器操纵负荷系统的力感模拟[7]、车辆控制中的助力转向系统等不以试验性能为目标的应用。为了满足不同设备的加载需求，加载系统的驱动方式除电液方式外，还出现了电动和气动方式，加载谱的形式有惯性负载、弹性负载、摩擦负载、静负载、可变负载以及动载叠加静载型负载等。

但加载系统存在一个不可回避的问题，即如何抑制被加载对象运动所引入的干扰(多余力)。多余力输出不仅影响力跟踪精度，而且降低了加载系统的闭环带宽，严重影响力控制性能。因此，为了保证仿真和试验的可靠性与置信度，加载系统的设计包含两个主要内容：力跟踪问题和多余力抑制问题[8]。本研究讨论目前多余力抑制方法的研究及进展。

1 多余力建模

对加载系统来说，实际的输出加载力和指令信号对应的期望加载力之间的误差称为加载误差。加载误差是由扰动和指令信号产生的。对加载系统而言，由被加载对象的位置扰动引起的加载误差远远超过其他扰动及指令信号所引起的加载误差，一般把位置扰动引起的加载力称为多余力。

不同类型的加载系统结构基本类似，一般都由加载机构、驱动装置、力(力矩)传感器以及控制器组成，工作时被加载对象的输出端与加载机构的输出端通过力(力矩)传感器刚性连接。我们以图1所示的直升机桨距调节液压助力器实验用电液伺服加载系统为例，进行多余力的分析。图1中，xM和xL分别表示桨距调节液压助力器活塞杆、加载液压缸活塞杆的位移。

根据液压控制理论，联立加载机构的支配方程，可以得到输出加载力FL与伺服阀开口量xv和桨距调节助力器位移xM之间的传递函数为[8]：

(1)

式中，AL为加载液压缸的有效工作面积(m2)；BL为加载液压缸的阻尼系数(N·s/m)；Kq和Ktm分别为加载端伺服阀流量增益(m2/s)和系统综合流量-压力系数(m5/(N·s))；mL加载端负载等效质量(kg)；VL为加载系统容腔和管路的总容积(m3)；βe为加载系统液压油的等效弹性模量(N/m2)；Ks为力传感器的刚度(N/m)。 式(1)说明，FL除与xv(控制信号)有关外，不仅与操纵侧助力器的运动速度有关，而且还跟运动的加速度以及加速度的变化率有关。只要被加载对象存在运动，多余力就不可避免，对加载力的输出产生干扰。

定义FL与xv和sxM(s)之间的传递函数分别为:

(2)

图1 直升机桨距调节液压助力器加载实验用电液加载系统

(3)

(4)

式中，Ksv为伺服阀增益(m/A)，ωsv和ζsv分别为伺服阀的固有频率(rad/s)和阻尼比。假设ur为控制量电流输入(A)，Fd为多余力干扰输入(N)，则可得简化后的加载机构方块图如图2所示。

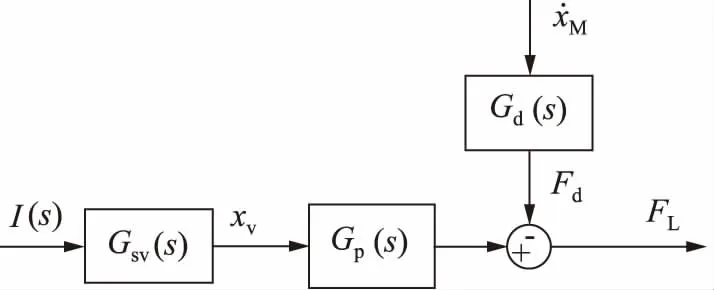
图2 加载系统结构简图

图3是一个具体的加载机构频率特性。由图3可知，多余力在低频段呈微分特性，随着频率的增加，其幅值以+20 dB斜率上升，降低了系统频宽；在中频段多余力基本上趋于饱和及稳定；而在高频段，随着频率的增加，其幅值以+60 dB斜率上升、相位急剧上升，当然，实际的位置扰动频率不会出现在此区域内。在多余力没有得到有效的抑制前，系统很难获得理想的加载性能。因此，多余力抑制问题是加载系统设计必须解决的首要问题。

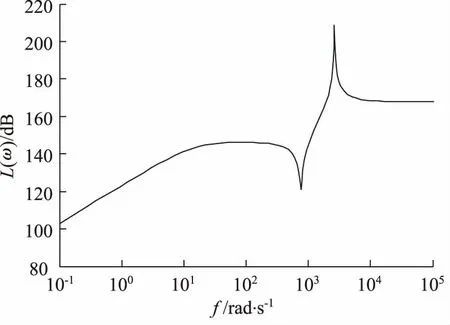
图3 助力器电液加载系统多余力幅频特性

2 多余力抑制

多余力既与加载系统的结构参数有关(如AL,VL,mL,Ks,Ktm)，也与扰动输入有关。因为扰动输入可以观测，采用扰动补偿抑制多余力更为方便。下面从两个方面讨论多余力抑制策略。

2.1 结构设计抑制方法

从结构设计角度抑制多余力的方法又可分为两类。一类是在系统物理结构设计及元件选择时，针对影响多余力的个别环节和参数进行合理选择和修正，其本质是通过增大液压或机械结构的滤波作用，在结构上减小被加载对象运动给加载系统带来的干扰，由于补偿原理的局限性，这类补偿只能消除部分多余力，且灵活性差。另一类结构设计抑制多余力方法是设法通过液压或机械方式消除加载系统的位置扰动，理论上可以达到完全消除多余力的目的，如双阀流量补偿和位置同步补偿方法。这类方法结构复杂、系统造价高和高频时同步控制实现困难。

第一类方法代表性的成果有：文献[9]采用降低连接刚度的方式设计负载模拟器，通过在负载模拟器与舵机之间用刚度较低的弹簧杆连接，减小舵机运动造成的多余力矩对负载模拟器的影响。但弹簧杆的引入同时也降低了系统的前向增益、频宽和快速性。文献[10]选用高频响的压力伺服阀或者大预开口的流量伺服阀来消除多余力，预开口伺服阀的压力-流量特性曲线的斜率特别大，对流量变化敏感性小，适应于被动式力伺服系统。但是国内生产的压力伺服阀和大预开口流量伺服阀的性能不稳定，频响较低，无法满足伺服加载系统的要求。

第二类方法代表性的成果有：文献[11]在加载马达的两负载腔之间相对于加载伺服阀并联一个补偿伺服阀，将加载马达的速度信号作为补偿阀的控制信号，对强制流量进行补偿，抵消强制流量引起的多余力矩。哈尔滨工业大学刘庆和教授等开发了一种带有位置同步补偿马达的双马达电液负载模拟器[12]，它在加载马达和基座之间引入一个位置同步补偿马达，同步马达与舵机受同一指令控制而同步运动，将原来的被动式加载系统近似转换为主动式，使作用在加载马达上的位置扰动接近于零。这类方案的机械机构复杂、体积大、成本较高、不易加工和维护、系统调试困难，而且要使位置同步马达很好地跟随不同的承载对象运动，需要设置不同的控制参数。位置同步系统的刚度和快速性会影响加载系统的控制精度，并且要求位置同步系统的频宽接近甚至超过承载系统，这样才能有较好的效果。

2.2 控制策略抑制方法

产生多余力的原因是被加载对象的位置变化扰动，这种位置变化是被加载系统工作所必须的。从如何对待和处理这种扰动的方式上，可以将控制策略抑制多余力的方法分为两类：一类按照扰动补偿的思想，为多余力设计独立的补偿环节，代表性方法有：结构不变性原理、速度同步补偿和多变量解耦控制；另一类则将加载系统的所有扰动作为一个整体予以考虑，代表性方法有：鲁棒控制、内模控制、干扰观测器、非线性方法和智能控制等方法。

1) 结构不变性原理

采用结构不变性原理克服多余力(力矩)的方法由北京航空航天大学刘长年教授在20世纪70年代末提出[1]。其原理是利用被加载对象的速度反馈信号来设计补偿环节Gcom(s)，实现补偿与扰动的对消，这种补偿属于开环补偿，不影响加载通道的系统结构及特性。本研究讨论的电液加载系统其补偿环节Gcom(s)可以设计为：

(5)

要实现完全的对消，必须满足两个条件：被加载对象的速度获取绝对准确以及设计的补偿环节Gcom(s)与实际系统模型完全匹配并且物理可实现。但是，实际系统的不确定性总是存在的，测量噪声和延时使准确的速度信号获取困难，补偿环节存在很难物理实现的高阶微分项，所以，在工程中只能近似实现结构不变性原理，多余力很难完全消除，而且补偿环节不具鲁棒性。虽然如此，近似实现结构不变性原理的补偿环节可以在低频位置扰动情况下消除多余力的绝大部分，而且其结构简单、实现容易以及利用的全部是系统的可测输出特点让它在工程中依然得到了应用。

文献[4]在海洋拖曳系统的电液负载模拟系统中采用了基于结构不变性原理的速度前馈补偿设计抑制多余力。文献[7]在飞行模拟器操纵负荷系统中，采用电液加载系统模拟飞行员操纵驾驶机构时的操纵力感，为了保证力感模拟的逼真度，采用结构不变性原理设计补偿环节消除操纵杆运动引起的多余力。文献[13]利用驱动伺服机构位置反馈信号进行辨识，构造理想的速度补偿信号进行流量前馈补偿，并利用最小二乘法在线辨识补偿信号修正相位。文献[14]在电动加载系统中，提出被加载对象电流前馈补偿法，使补偿环节微分阶数降低两阶，降低了实现难度。

2) 速度同步补偿

为了解决结构不变性原理中被加载对象速度获取问题，寻找相位滞后和噪声小的速度信号，速度同步补偿[15]方法通过利用被加载舵机的伺服阀控制信号近似获得扰动速度再采用结构不变性原理实现多余力矩的抑制，该方法的依据是阀控位置伺服系统的数学模型在低频段近似为一个积分环节，那么伺服阀输入指令作为积分环节的输入，实际上就是舵机系统的速度指令。速度同步补偿器采用PD控制器设计其传递函数，以提取系统最超前的速度和加速度信号。严格地讲，该方法应称为“速度同步获取补偿法”，否则容易引起歧义。利用舵机伺服阀输入指令作为速度信号，其准确性和平滑度明显优于直接从舵机位置输出微分获取速度信号，因而取得了比结构不变性原理好的多余力抑制效果。速度同步补偿是基于结构不变性原理的，因此这种补偿具鲁棒性不好。

文献[16]对电液加载系统设计了一种双环控制方式，引入位置同步环对舵机运动干扰进行解耦。文献[17]设计了一个非线性参数估计的自适应非线性补偿器提高了多余力补偿环节的鲁棒性。

3) 多变量解耦控制

多变量解耦控制工作原理是取被加载对象和加载系统的输入信号和输出信号分别作为输入量和输出量，将整个系统看成是多变量系统，引入解耦控制器，应用前馈控制的原理，解除控制回路的耦合，适当选择解耦器参数消除多余力。文献[18]尝试运用解耦控制方法来克服负载模拟器的多余力矩，设计的控制器中含有较强的微分环节，物理上难以实现，在实际中要对其进行简化，只能实现近似解耦。文献[19]为了解决阀控非对称缸负载模拟器多余力矩的干扰问题，加载伺服阀采用流量-压力伺服阀，位置伺服阀采用流量阀，然后设计解耦控制器，提高了加载系统的跟踪精度和频带宽度，同时也提高了被加载系统的控制性能。文献[20]提出了自适应最优解耦控制策略，有效消除了助力器与加载通道以及加载通道相互之间的耦合作用，提高了加载指令的跟踪精度。

但这种方法不仅需要知道加载系统的准确数学模型，而且要知道被加载系统的准确数学模型。因此，系统模型的不确定性以及被加载对象的不可知性限制了这种抑制方法的应用。

4) 鲁棒控制

为了弥补对数学模型的过分依赖，并综合考虑参数变化、模型变动和外来干扰等不确定性，要求加载系统具有鲁棒稳定性和鲁棒性能，这符合鲁棒控制设计思想。鲁棒控制理论以基于状态空间模型的频率设计方法为主要特征，对系统的频域特性进行整形，同时考虑系统的抑制扰动特性和鲁棒性要求，是解决控制对象模型不确定性和外界扰动不确定性问题的有效方法。加载系统进行鲁棒控制设计时，被加载的运动干扰被看作外部干扰的一部分，把最大扰动情况作为系统的扰动抑制指标，并结合系统对指令跟踪和不确定性抑制的要求来设计反馈控制器，通过提高加载系统的鲁棒性来消除位置系统的影响，即消除多余力。方法有定量反馈控制、H∞控制、μ综合设计等。

文献[21]采用混合灵敏度方法设计了航空舵机电液负载模拟器的鲁棒控制器，仿真结果表明系统符合“双十”指标。文献[22]将加载系统鲁棒性问题转化为线性矩阵不等式(LMI)问题，给出了问题的一个凸约束条件，不需要预先调整任何参数和正定对称矩阵，从而大大降低了问题求解的保守性。文献[23,24]在加载系统鲁棒控制设计时，将系统的不确定性分散成多个小的不确定性摄动块，采用μ综合设计，在H∞设计中导入定标函数改善系统的鲁棒性能，最大程度地降低设计的保守性。文献[25]利用定量反馈方法、文献[26]采用在线调整的定量反馈技术分别设计了加载系统的鲁棒控制器。

由于加载系统的多余力属于强干扰，其强度远远超出系统其它所有的干扰，用最大扰动情况作为系统的扰动抑制指标，系统的鲁棒性要求限制了力跟踪性能的提高，设计得到的鲁棒控制器具有一定的保守性。

5) 内模控制

内模控制作为一种独特的控制系统结构，采用被控对象的内部模型和反馈修正的先进控制策略。其设计思路是将对象模型与实际对象并联，设计控制器逼近模型的动态逆，并通过附加反馈低通滤波器以增强系统的鲁棒性。内模控制不需要深入了解工作过程的内部机理，也不需要通过复杂的系统辨识辨识模型。内模控制具有良好的跟踪调节性能、鲁棒性能，能消除不可测干扰的影响，且结构简单、设计简便，在线调节参数少，因而被广泛采用于抑制控制系统扰动问题。文献[27]在用频率测试法对电动加载系统的标称模型进行辨识的前提下，设计了加载系统内模控制器，实现多余力矩的抑制和消除，并将反馈低通滤波器的求解问题转化为标准的H∞问题求解。文献[28]采用内模控制方法设计了内模控制器抑制多余力矩，采用混合灵敏度方法设计了串联控制器使系统达到闭环带宽要求。

6) 干扰观测器

干扰观测器的设计方法是利用系统的输入、输出信号通过加载模型的标称逆模型，观测出系统的等效输入干扰，并通过低通滤波器Q(s)将等效补偿输入到控制输入端，实现干扰的抑制，同时使系统近似于标称模型，提高系统的鲁棒性。基于扰动观测器的设计方法通常为双回路结构：内回路补偿器抑制系统的等效输入干扰，使实际系统变成给定的标称模型，并满足鲁棒性要求；外回路控制器满足性能指标要求。它具有计算量小、实时好、不需额外的传感器等优点。干扰观测器的设计关键是低通滤波器Q(s)的设计。采用常规的方法进行Q(s)设计很不方便，可以转化为鲁棒内回路的H∞混合灵敏度问题设计[29]。文献[30]采用扰动观测器补偿的方法对电动式舵机负载模拟器的多余力进行了动态补偿，取得了很好的控制效果。文献[8]采用干扰观测器补偿的方法在直升机桨距调节助力器电液加载系统中的取得了较为理想的多余力抑制效果。

扰动观测器只是在低频段将负载模拟器系统近似为标称模型，这方便了系统外回路控制器的设计，但系统在中高频段存在的干扰和不确定性等没有被考虑，所以不能保证系统高频时的性能。而且采用鲁棒内回路的混合灵敏度方法设计Q(s)时的权函数物理意义不太明确。

7) 非线性方法

当前非线性控制理论已经取得了显著的研究和应用成果，对于加载系统这类具有明显非线性特征的系统，采用非线性方法进行控制器设计是非常合适的。加载系统的非线性设计方法主要研究系统的非线性特性和参数的不确定性，被加载对象的运动干扰被作为外部干扰的一部分。

文献[31]提出一种基于反步控制的全状态反馈控制方法，利用Lyapunov函数的稳定性定理保证了设计控制器的稳定性，在建立系统非线性模型的基础上，将系统方程重组成多个虚拟子系统，利用反步控制思想对每个虚拟系统设计虚拟控制量，进而一步步反向推导出含有加载系统和被加载系统各个状态量的非线性控制器。文献[32,33]采用了反步控制算法调整参数的非线性自适应方法。文献[34]采用反演设计算法并设计GCMAC神经网络逼近系统不确定性，从前向后逐步递推得到了系统的控制Lyapunov函数，设计了自适应反演控制器，确保系统稳定且输出跟踪误差渐近收敛于零，有效解决了位置扰动和系统参数不确定性问题，提高了载荷谱跟踪精度。文献[35]采用非线性定量反馈技术先设计了一个鲁棒反馈控制器使力控制闭环对伺服阀流量、压力的非线性和系统的典型不确定性不敏感，然后在QFT的框架下设计了一个针对运动干扰的补偿器来提高力跟踪的带宽。

8) 智能控制

智能控制主要包括专家控制、模糊控制、神经网络控制、多模变结构智能控制、学习控制和自学习控制、仿人智能控制和混沌控制等。其中，神经网络控制在加载控制系统研究中应用较为广泛。神经网络控制的基本思想是从仿生学的角度，模拟人脑神经系统的动作方式，使机器具有人脑那样的感知、学习和推理能力，神经网络不需要知道系统的准确模型，具有能够以任意精度逼近任意连续非线性函数，对复杂不确定问题具有自适应和自学习能力等优点。

文献[36]利用神经网络非线性逼近和自学习特性，为电动加载系统设计了一种参数自整定智能PID控制器。文献[37]利用对角回归神经网络(DRNN)与PID并联进行控制与调节的控制方法，速度信号作为神经网络的参考输入，使系统具有了很好的自适应消扰能力。文献[38]采用多层前馈神经网络对系统进行辨识和控制等方法来减小不确定性以及外扰动的影响，自适应逆控制中的反馈在自适应迭代过程中只用于改变模型参数，避免了因反馈而可能引起的不稳定问题，同时使系统动态特性的控制与对象扰动的控制分开而互不影响。文献[39]采用改进的CMAC神经网络与PID控制器并联构成复合控制结构，改进的CMAC利用存储单元的先前学习次数作为可信度，消除了常规前馈型CMAC的过学习现象。文献[40]采用自适应CMAC神经网络与自适应神经元控制器并联构成复合控制结构，以系统的指令输入和实际输出作为CMAC的激励信号，以系统的当前控制误差为CMAC的训练信号，利用误差在线自适应调整学习率，消除了常规前馈型CMAC的过学习和不稳定现象。文献[41]提出了随动系统负载模拟器一种基于改进的自学习函数扩展小波神经网络智能控制器，在误差大时采用Bang-Bang控制，误差小时采用基于函数扩展的小波神经网络和模糊补偿控制，同时采用基于改进的差分演变算法来估计控制器的参数。文献[42]提出了一种具有输出平滑性的改进CMAC+PD复合控制算法，该方法通过新的权值更新公式，在权值更新时直接达到减小误差和提高输出平滑性的目的。

但是，随着加载系统加载指标的提升，如加载力矩从0.1 N·m超小力矩到70000 N·m超大力矩，多余力从原来消除80%提升到95%以上，加载力的频率响应也从低频0.02 Hz到高频80 Hz等，尤其是中小力矩和高频位置扰动加载的高精度加载的要求，独立采用一种多余力抑制方法往往很难达到实现加载要求的多余力抑制要求。

2.3 多余力复合抑制方法

根据以上对多余力抑制方法的分析，虽然在低频加载系统设计中取得了一定的成果，但是可以看到，如果不针对多余力设计鲁棒补偿，难以在参数摄动情况下获得满意抑制效果。于是，很多学者在加载系统控制方案设计时都提出了与前馈补偿相结合的复合控制方案，在实现更理想的多余力抑制效果的同时提高加载系统的鲁棒性。

李运华等在1998年就提出了一种按职能分工的复合多余力抑制方法[43-45]，首先设计了一个基于结构不变性原理的定常补偿器，抑制多余力矩的影响，然后设计一个内环鲁棒自适应控制器，用来提高补偿多余力矩通道的鲁棒性，外环设计一个2阶无静差控制器满足跟踪连续时变参考信号的要求。

文献[46]设计了H∞鲁棒控制和基于结构不变性原理前馈补偿相结合的加载系统复合控制器，前馈补偿包含速度补偿和加速度补偿项，H∞混合灵敏度问题采用LMI的方式进行求解，在中低频取得了很好的多余力抑制效果，并保证了系统的鲁棒性和稳定性，但是由于没有进行加速度变化率的补偿，在高频出现了性能的弱化。

文献[47]为了保证电动负载模拟器力矩精确地加载，设计了基于迭代学习控制和舵机位置前馈补偿结合的复合力矩控制器，引入了舵机位置前馈补偿，并设计基于指令力矩幅值和相位修正的迭代学习控制器，基于P型控制器实现对幅值和相位的迭代学习。

文献[48]采用经典控制和现代控制相结合的复合控制策略，从按职能分工的角度设计控制器，将前馈、神经网络以及传统的校正控制相结合。利用前馈消除由角位移引起的线性定常多余力矩；利用神经网络消除非线性等因素引起的多余力矩(如由角加速度和角加加速度引起)，同时提高系统的响应速度。并且由于神经网络的非线性辨识能力，使系统表现出很好的鲁棒性。

文献[49]采用速度前馈补偿与前馈逆模型观测器相结合的方法在飞行模拟器操纵负荷系统的力感模拟系统中进行系统多余力的抑制，前馈逆模型观测器对速度前馈补偿后的剩余多余力进行二次抑制。

在考虑系统的不确定性并结合扰动补偿进行多余力抑制方面，最近已取得相关成果，文献[50]提出了一种速度前馈补偿并采用双环串级控制策略的复合多余力抑制方案，如图4所示。首先，通过一个速度定常补偿器消除由速度引起的多余力的绝大部分，内环控制采用基于扰动观测器的设计来补偿由多余力的剩余部分以及系统中的其他干扰所组成的等效输入干扰，进一步抑制多余力，并增强系统的鲁棒性，使系统在一定频带范围内近似为一个标称模型，如果设计基于双环串级控制策略的鲁棒外回路控制则能进一步提高系统的加载精度及改善系统在高频区域的鲁棒性。

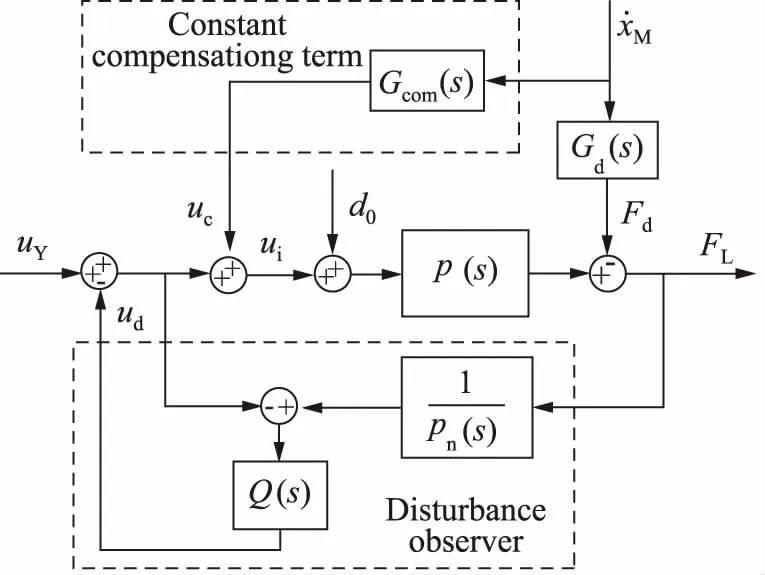
图4 多余力复合抑制方案

这种方案与文献[43]类似，加载系统的控制输入ui(相当于伺服阀的线圈电流)由三部分组成：

ui=ur+uc-ud

(6)

式中，uc为消除多余力的补偿输入；ud为补偿所观测的系统等效输入干扰的干扰补偿；ur为跟踪力指令的控制输入。

在这种复合抑制方案中，扰动观测器的设计关键是低通滤波器Q(s)的设计，采用文献[29]提出的一种系统化的优化方法设计Q(s)，通过定义一个辅助控制器K(s):

(7)

其中，K(s)为一个稳定的传递函数，可将Q(s)的设计转化为K(s)的求解。这样通过求解H∞混合灵敏度问题得到K(s)，然后就可得到Q(s)。

图5表示所提出的复合补偿方案在系统供油压力存在摄动情况下的多余力抑制仿真结果。仿真时，运动干扰为7sin14t(mm/s)，指令力输入为0，系统标称工作压力为21 MPa，速度采用直接微分的方式获取。

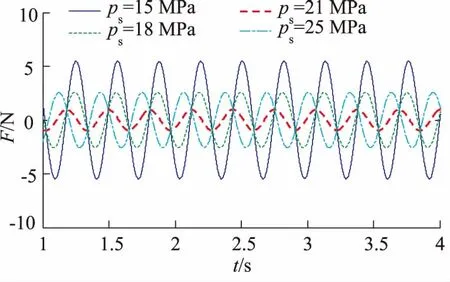
图5 复合多余力补偿对供油压力摄动的多余力抑制效果

从图5的仿真结果可以看出，采用复合抑制方案，多余力得到了有效的抑制，剩余的多余力基本上趋于0，而且，在模型摄动时，多余力的抑制也表现出很好的鲁棒性。

3 结论

多余力的抑制是加载系统设计中的一个关键问题，有效地抑制多余力是取得期望加载性能的前提条件。任何一种消除多余力的方法都有其局限性，要从系统结构设计和控制策略两方面考虑，将多种方法有机地结合起来，寻找一种合理并有效的方式，才能取得理想的抑制效果。

参考文献：

[1] 刘长年.液压伺服系统优化设计理论[M].北京:冶金工业出版社,1989.

[2] 池谷光荣.油圧式模擬負荷系の有用性评价[R].航空宇宙技術研究所报告,1975.

[3] 薛红军,邓攀,张国龙.船舶舵机加载系统多余力抑制控制策略[J].船舶工程,2014,36(5):77-85.

[4] 杨钢,刘迎雨,杜经民,李宝仁.基于模糊PID控制器的电液负载模拟系统[J].华中科技大学学报(自然科学版),2012,40(4):59-62.

[5] 郑玉才,刘涛,刘长荣.车辆悬挂系统液压负载模拟器设计[J].农业机械学报,2007,38(7):16-18.

[6] Radpukdee T., Jirawattana P. Design of an Engine Load Simulator[A]. ASME International Mechanical Engineering Congress and Exposition [C]. 2005:17-25.

[7] 赵劲松,叶正茂,韩俊伟.飞行模拟器操纵负荷系统内回路的逆模型控制[J].西安交通大学学报,2012,46(4):38-44.

[8] Yunhua Li, Zhiqing Sheng, Shaoping Wang. Design of Disturbance Observer of Electro-hydraulic Loading System for Helicopter Manipulating Booster[C]. The Fourteenth Scandinavian International Conference on Fluid Power, SICFP15, May 19-21 2015, Tampere, Finland.

[9] 郝经佳,赵克定.一种采用弹簧挠性连接的电液负载仿真台的设计方法[J].机床与液压,2001,(1):59-60,106.

[10] 李阁强,韩建海,张彪,等.正开口阀在电液负载模拟器中的应用[J].液压与气动,2007，(12):42-44.

[11] 王经甫,叶正茂,李洪人.双阀并联控制在船舶舵机电液负载模拟器多余力抑制中的研究[J].机械工程学报,2005,41(4):229-233.

[12] 张立勋,王安敏,周继成,等.位置同步补偿提高飞行器负载模拟器频宽的研究[J].哈尔滨工业大学学报,1995,27(3):123-126.

[13] 张金英,赵英娜,延皓,李长春,孙萌.电液伺服负载模拟器多余力补偿及控制策略[J].北京交通大学学报,2014,38(1):146-152.

[14] 李瑞,王明艳.电动负载模拟器抑制多余力的结构补偿控制[J].机床与液压,2013,41(3):62-64.

[15] 焦宗夏,华清,王晓东,等.电液负载模拟器的复合控制[J].机械工程学报,2002,38(12):34-38.

[16] Wang Chengwen, Jiao Zongxia, Wu Shuai, Shang Yaoxing. An Experimental Study of the Dual-loop Control of Electro-hydraulic Load Simulator (EHLS)[J]. Chinese Journal of Aeronautics,2013,26(6):1586-1595.

[17] Yao Jianyong, Jiao Zongxia, Shang Yaoxing, Huang Cheng. Adaptive Nonlinear Optimal Compensation Control for Electro-hydraulic Load Simulator [J]. Chinese Journal of Aeronautics,2010,(23): 720-733.

[18] 胡庆超,余蔚淳.多变量电液加载系统的解耦[J].液压与气动,1988，(3):28-29.

[19] 李阁强,李水聪,黄飞.阀控非对称缸被动式电液力伺服系统的解耦控制研究[J].机床与液压,2013,41(1):7-10.

[20] 袁朝辉,张伟,穆旭.直升机旋翼协调加载自适应最优解耦控制[J].中国机械工程,2007,18(22):2691-2696.

[21] 袁锐波,赵克定,李阁强,罗璨.基于混合灵敏度方法的负载模拟器的控制研究[J].南京理工大学学报,2006,30(5):537-541.

[22] 王燕山,李运华,王益群.基于LMI的电液伺服加载系统多目标鲁棒控制[J].北京航空航天大学学报,2007,33(8):911-914.

[23] 齐潘国,王慧,韩俊伟.基于结构化奇异值设计方法的液压操纵负荷系统鲁棒控制[J].吉林大学学报(工学版),2011,41(4):1004-1009.

[24] 李阁强,赵克定,袁锐波.miu理论在电液负载模拟器中的应用[J].航空学报,2007,28(1):228-233.

[25] Nam Y, Hong S K. 2002. Force Control System Design for Aerodynamic Load Simulator [J]. Control Engineering Practice,2002,10(5): 549-558.

[26] Dinh Q T, Ahn K K, Yoon J I. A study on Force Control of Electric-hydraulic Load Simulator Using an Online Tuning Quantitative Feedback Theory[C]. International Conference on Control, Automation and Systems,2008,2008:2622-2627.

[27] 史航. 基于内模控制的电动负载模拟器伺服系统设计[D].哈尔滨:哈尔滨工业大学,2007.

[28] 袁兵,吴维峰,姚郁.基于内模方法的电动负载模拟器控制系统设计[J].系统仿真学报,2009,21(2):122-125.

[29] Kim B K, Choi H T, Chung W K. 2002. Analysis and Design of Robust Motion Controllers in the Unified Framework[J]. ASME Journal of Dynamic System, Measurement, and Control,2002,124(2):313-321.

[30] 方强,姚郁.电动负载模拟器扰动观测器系统优化设计[J].哈尔滨工业大学学报,2007,39(3):349-353.

[31] 张彪,赵克定.基于反步控制的被动力伺服系统全状态反馈控制[J].西安交通大学学报,2008,42(1):82-86.

[32] YAO Jianyong, JIAO Zongxia, YAO Bin, et al. Nonlinear Adaptive Robust Force Control of Hydraulic Load Simulator[J]. Chinese Journal of Aeronautics,2012,(25):766-775.

[33] Chengwen Wang, Zongxia Jiao, Shui Wu, Yaoxing Shang. Nonlinear Adaptive Torque Control of Electro-hydraulic Load System with External Active Motion Disturbance[J]. Mechatronics,2014,(24):32-40.

[34] 张伟,穆旭,袁朝辉,李昆.基于自适应反演的电液负载模拟器设计[C].Proceedings of the 25th Chinese Control Conference, 2005: 253-255.

[35] Mark Karpenko, Nariman Sepehri. Electrohydraulic Force Control Design of a Hardware-in-the-loop Load Emulator Using a Nonlinear QFT technique[J]. Control Engineering Practice,2012,(20):598-609.

[36] Han Huatao, Yang Bo. A CMAC Based Self-tuning Intelligent PID Controller for Electric Load Simulator[C]. Third International Conference on Instrumentation, Measurement, Computer, Communication and Control, 2013:1443-1448.

[37] 华清,焦宗夏.负载模拟器的DRNN神经网络控制[J].机械工程学报,2003,39(1):15-19.

[38] 袁朝辉,李凌.基于自适应逆控制的无人机负载模拟器复合控制[J].西北工业大学学报,2005,23(2):256-260.

[39] 杨波,王俊奎.基于改进的CMAC的电动加载系统复合控制[J].航空学报,2009,29(5):1314-1318.

[40] 杨波,王哲.舵面电动加载系统的自适应CMAC复合控制[J].北京航空航天大学学报,2010,36(3):333-337.

[41] 王超,刘荣忠,侯远龙,高强,王力.基于改进WNN的随动负载模拟器研究[J].系统仿真学报,2015,27(2):344-351.

[42] 杨波,程龙.提高电动加载系统输出平滑的CMAC复合控制[J].北京航空航天大学学报,2013,39(6):723-727.

[43] 李运华,焦宗夏,王占林.舵机力矩负载模拟器的混合控制方法研究[J].航空学报,1998,19(7):60-64.

[44] 李运华.抑制电液力矩控制系统的多余力矩的新方法[J].机械工程学报,2000,36(3):4-7.

[45] Yunhua Li. Development of Hybrid Control of Electro-hydraulic Torque Load Simulator [J]. ASME Journal of Dynamic Systems, Measurement, and Control, 2002,124(3):415-419.

[46] Jingfu Wang, Lihua Liang and Songtao Zhang, et al. Application ofH∞Control Based on Mixed Sensitivity in the Electro-hydraulic Load Simulator[C]. Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation,2007:2991-2996.

[47] 牛国臣,王巍,宗光华.基于迭代学习的电动负载模拟器复合控制[J].控制理论与应用,2014,31(12):1740-1747.

[48] 袁朝辉,徐鹏,朱伟,何长安.基于神经网络的无人机负载模拟器的复合控制[J].计算机仿真,2006,23(3):37-40.

[49] Jinsong Zhao, Gang Shen, Chifu Yang, et al. Feel Force Control Incorporating Velocity Feed Forward and Inverse Model Observer for Control Loading System of Flight Simulator[J]. System and Control Engineering, 2012:1-15.

[50] Zhiqing Sheng, Yunhua Li. An Improved Hybrid Suppression Method for Extraneous Force of High-frequency Electro-hydraulic Loading System[C].IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM2015, July 7-9，2015, Bussan, Korea.