桥梁汽车荷载响应的极值外推方法综述
阮 欣,周军勇,石雪飞
(同济大学 桥梁工程系,上海200092)
汽车荷载是公路及桥梁结构的主要可变荷载,是影响结构安全与耐久性能的重要因素.近期,汽车荷载相关量测技术迅速发展[1],获得了大量的车辆及荷载数据,为汽车荷载及其响应的研究提供了广泛基础.在此基础上,桥梁汽车荷载响应评估及荷载模型研究正成为新的热点[2-4].极值外推是基于短时汽车荷载响应数据预测长周期极端值的重要方法,然而,汽车荷载随机性大、时变性强,使得荷载响应及其分布也具有高度不确定性,如何选择有效的外推方法预测极值,并保证外推精度和效率,一直是研究的重点与难点[5].
论文将系统介绍桥梁汽车荷载响应的主要极值外推方法,分析各方法的基本原理和应用状况,研究影响极值外推的关键参数,并基于实测的动态车辆称重数据(动态称重系统测取,weigh-in-motion,WIM),比较研究各种外推方法的适用状况、外推效率及精度,探索桥梁汽车荷载响应极值外推的研究与发展方向.
1 主要外推方法
极值理论是研究小概率事件极端值变异性的建模与分析方法,最早用于极端自然灾害如地震、台风、洪水等的预测[6],随着风险控制理念的推广与应用,小概率事件的分析逐渐受到广泛关注,并拓展到各类极端风险事件的对策研究中.
汽车荷载在不同的交通组成和运营状态下,对桥梁结构的响应呈现显著差异.然而,对于结构的设计和评估,往往仅需关注重现期内汽车荷载引起的极端响应,实际条件下考虑测试数据的代价和计算效率,只能获取有限时长范围内的荷载响应时程,因此基于数据样本时间的不对称及关注的极值特性,促成了极值理论在汽车荷载领域的应用.
目前桥梁汽车荷载研究中使用的极值外推方法,可总结为:基于随机变量假定拟合经验外推、基于经典极值理论的最大值外推、基于穿越次数的Rice公式外推和基于数值模拟的极值统计规定等4类.
1.1 基于随机变量假定拟合经验外推
早期,针对短时车辆数据无法满足长回归周期的 可 靠 度 计 算 问 题,Nowak[7-8],Moses[9]和Sivakumar[10]等将车辆荷载响应假定为随机变量,通过对随机变量经验分布的拟合,获取相关参数并进行高可靠度水平的直线外延,获取相关极值.
Nowak等[7-8]在美国早期的桥梁设计规范中率先采用正态概率纸直线外推方法,通过安大略省交通管理部门收集的卡车数据,评估了设计基准期75年的荷载响应极值.基本原理是:首先,基于车辆数据对效应影响面的加载求荷载响应时程,计算的基础数据容量为n,时长m,d;其次,将荷载响应累积概率分布绘制于正态概率纸上,并根据数据的尾端走势进行直线拟合外延;最后,基于结构设计基准期T最大值累积概率水准p=1-m/(365nT),计算可靠度水平Φ-1(p)对应的荷载响应极值.
Nowak方法[7-8]实质是假定荷载响应的尾部满足正态分布,考虑了所有数据样本,根据经验取用部分尾部数据直线拟合外延,但是尾部数据的选择没有明确说明,导致外推极值离散性较大,可能会估测偏高.对此,Moses[9]在 Nowak[7-8]基础上只选择高端的20%数据,根据选择数据的均值μ20%与方差σ20%计算设计基准期T的荷载响应极值的均值Emax.Emax=μ20%+tσ20%,其中t=Φ-1(1-m/(0.2×365nT)).该研究成果直接应用于美国国家公路与运输协会(AASHTO)组织编写的《桥梁评估活荷载系数校核》报告中.
Moses[9]方法使用直观简便,避免了 Nowak[7-8]数据选择直线外推的主观性,但该方法无法计算设计基准期内的最大值方差,误差会累积从而降低外推的精度.Sivakumar[10]则在 Moses[9]基础上改进,在选择高端5%数据基础上,计算了设计基准期内的最大值均值μ和方差σ如式(1),该方法用于美国公路合作研究项目(NCHRP)的研究报告《交通数据在桥梁设计中的应用》中.

式中:N为测方式数据的容量的5%;μ5%,σ5%分别为尾端5%数据的均值和方差;μ,σ分别为设计基准期T内最大值的均值和方差.
上述三种典型方法均假定正态分布能描述荷载响应尾部走势,通过对样本的正态分布参数估计,计算关注极值的统计特征.该方法能高效获取荷载响应极值,对于数据样本的利用率很高,能够快速外推响应极值,适用于桥梁汽车荷载响应的快速评估,也关注到了荷载响应的尾端数据走势是评估荷载响应极值准确性的关键.然而,该外推方法的客观性不强,外推精度较难把握.首先,荷载响应尾部采用正态分布拟合的可信度如何评估需要研究;其次,极值外推关键是尾部数据,到底选取多少数据不会影响外推的准确性需分析;最后,荷载响应极值的可靠度标准不统一,受每天观测的基础数据量影响.
1.2 基于经典极值理论的最大值外推
根据经典极值理论,如若数据样本之间满足独立同分布假定,且采用的基础底分布能够完全描述数据的分布特征,则样本的最大值分布函数就可以精确地表达,如式(2)所示.

式中:X1,…,Xn是独立同分布随机变量;F(x)是底分布;Pr(Mn≤x)是最大值分布.
基于经典极值理论,诸多学者进行了车辆荷载响应极值的研究工作,其中公路桥梁车辆荷载研究课题组[11]就是采用上述方法,对车辆荷载响应数据进行优度检验,认为一般运行状态下最大值分布满足韦伯分布,密集运行状态下满足正态分布,以此外推荷载响应极值.
经典极值理论的问题是,实际中寻找能够完全描述基础样本特性的底分布是很难实现的,只能研究样本的渐进分布.因此,在上述基础上,极值类型定理得到了广泛应用.Fisher-Tipper定理[6]认为,满足独立同分布的基础随机变量,根据极值渐进性,数据的最大值分布都可以归类到三种极值分布中,且这三种极值分布可以采用统一的表达形式描述(如式(3)),称为广义极值分布(generalized extreme value distribution,GEV分布).

式中:μ,σ,ξ分别为位置参数,尺度参数和形状参数
渐进极值理论为车辆荷载响应极值研究提供了理论 基 础,O'Brien[12],O'Connor[13],Caprani[14],Fu[15]等采用渐进极值理论对不同交通状态下汽车荷载响应进行了极值预测,并用于结构的状态评估、荷载模型修正中.然而,上述方法存在的主要问题是,如何构建最大值样本以及如何验证最大值样本拟合的准确性.
构建最大值样本,目前研究主要有三种方法:①确定样本区间(1d、1月或者1年),只选取区组最大值(block maxima method)作为极值观测样本[16];②对样本进行排序,建立次序统计模型(order statistics method),选取区组的最大r个数据作为极值观测样本[17];③ 确定区组数据阈值,如果数据满足独立同分布假定,则超阈值的样本分布(peaks over threshold method)可以用广义 Pareto分布描述[18-19].可知,上述方法都面临样本区间选择问题,一些学者取用一定时段作为样本区间[18],还有学者选用1月作为样本区间[16],总体而言,区间大小的选择应该尽可能满足样本之间符合独立同分布假定,但是区间长度的选择又面临样本数据利用率问题.考虑汽车荷载的时变特性,综合数据利用率,笔者认为,取用1d作为样本区间较能兼顾.此外,次序统计模型和阈值模型虽能更多利用单组样本的极值信息,但是序数及阈值的确定,目前还没有统一的方法,而这是影响极值拟合准确性的关键.
综上,基于经典极值理论的最大值外推方法具有客观的理论基础,但是存在数据利用率低的问题,当样本有限时,外推极值的变异性可能较大,导致完整意义上的极值估测的准确性较难把握.因此,解决基础数据量问题,是最大值外推方法在车辆荷载响应研究中的主要障碍.
1.3 基于穿越次数的Rice公式外推
穿越次数(level crossing method)是另外一种预测随机过程极端值的方法,对于均方可微的随机过程,可构建其穿越次数分布图,基于穿越次数与荷载响应重现期的关系,建立极值预测模型.美国学者Rice率先对随机过程的穿越界限问题进行了研究,建立了给定时间内基于平稳高斯过程穿越次数期望值的数学模型[20],如式(4)所示:
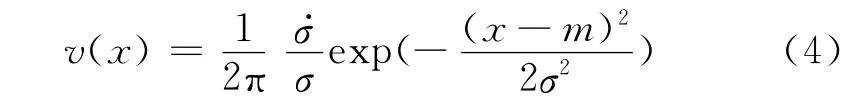
式中:σ、和m分别是X的标准值、随机过程导数X·的标准差和平均值;
Rice理论为汽车荷载响应极值预测提供了一种方法,随后Ditlevsen证明[21-22],对于大跨桥梁,汽车荷载是一个随机过程,考虑到结构效应影响面分布范围长,如若影响面的分布是随跨长变化的非零值,且影响区域相比单个重车所占区域显著大,则可将车辆荷载响应模拟为白噪声过程.此外,如果影响面随加载长度变化足够缓慢且连续,而桥跨长度与连续车辆的间距比值足够大,则该车辆响应满足平稳高斯过程,可用Rice公式预测响应极值.
Rice公式提供了穿越次数直方图尾部拟合的简化方法,充分利用了包含在荷载响应时程中的所有信息,能够高效地利用数据.然而,Rice公式拟合同样需要解决拟合的准确性的问题,研究表明[23],数据的拟合起点、区间分组长度和检验的显著水平是决定Rice公式外推准确性的关键.初期,相关学者都是根据经验方法确定Rice公式拟合起点[23],随后Cremona[24-25]引入 Kolmogorov-Smirnov(K-S)检验方法针对尾端不同效应拟合起点进行优度检验,从而确定最优起点用以荷载响应极值计算,并探讨了区组长度和检验显著水平的影响,研究成果用于实桥的换索评估及局部疲劳寿命预测中.
改进的Rice公式外推方法解决了拟合起点选择经验性问题,但在寻找最优拟合起点、最优分组区间及适宜显著水平上,仍需通过反复试算确定,外推的效率不高.此外,不同荷载响应是否都能够用Rice公式拟合,采用其他经验公式拟合,其准确性等问题,都需要进一步的研究.
1.4 基于数值模拟的极值统计规定
极值外推是解决预测极值与统计数据时长、可靠度水准等信息不一致问题,数值模拟的极值统计推定则是采用数值模拟方法(如蒙特卡洛方法),获取结构效应大范围长时间回归周期的荷载响应时程,以此取定样本给定可靠度标准的极值.O'Brien[26]尝试生成长达10 000年的车流模拟数据,将基于短时间随机车流响应特性的“极值外推”转化长时间车流响应的“统计推定”.
数值模拟的极值统计方法计算代价很高,假定双向八车道车辆日均交通量为80 000,设计基准期100年,则计算最大值样本的其中一个样本需要产生的随机数将达到29.2亿,即便选取基础数据的高端10%或5%进行模拟,随机数的产生及程序的计算效率也是该方法的主要弊端,存在很大局限.
2 影响极值外推的参数分析
目前的桥梁汽车荷载响应极值外推方法中,方法的客观性、数据利用率、外推效率与外推极值准确性等,是评价外推方法适用的标准.这其中,基础数据和底分布拟合是影响极值外推的关键参数.
2.1 基础数据
基础数据的测量精度、数据时长等,会显著影响荷载响应是否表达结构真实车辆服役状况,从而影响极值外推.目前,动态车辆数据多通过WIM系统采集,车辆的行驶速度、路面平整度及测试地址等与WIM数据测试精度高度相关[27].然而,经过 WIM设备传感技术的发展,现有的WIM数据精度都能够满足工程计算需求[27].
此外,考虑车辆荷载的显著时变性,基础数据的时长也是影响极值预测的关键.目前,诸多学者采用不同时长的数据进行荷载响应极值外推,Pan[28]用5 d的模拟车流数据作为荷载响应计算基础,O'Connor[3]利用实测4d数据模拟更长时间的随机车流.然而,基础数据应该采用多长时段,才能反映桥梁汽车荷载响应特征以支持极值外推,需要关注.
选取国内某高速实测28d的四车道WIM数据(该数据是基于连续28d共1 082 195辆车的测试结果),统计车重的特征参数随累积时长的变化规律如图1所示.考虑到极值研究重点关注高端尾部数据,且最大值数据的出现具有随机性,单纯统计最大值数据随累计时长变化规律意义不大,分析数据高尾部分的走势,才能较为准确地估测极值,因此研究中分别取所有数据、20%高尾、10%高尾和5%高尾数据分析.图1a和1b分别是各累积天数均值(经过对21d数据均值规整化处理)和变异系数随累积时长的变化规律.发现,统计参数在21d后基本趋于稳定,车重高端数据离散性也很小.说明,在条件允许下,应该选择至少3周实测车辆数据进行荷载响应计算及极值外推,才能基本反映实际车流对桥梁的作用状况.

图1 数据统计特征参数随累计时长的变化规律Fig.1 Change regulation of time-dependent characteristic parameters of data statistics
2.2 底分布拟合
底分布是描述外推数据样本特性的关键,车辆荷载研究重点关注最不利响应,因此底分布应该尽可能描述数据的尾部走势.基于随机变量假定拟合经验外推,底分布就是所选择基础数据样本的经验分布;经典极值理论的最大值外推,底分布是最大值样本分布;基于穿越次数的Rice公式外推,穿越次数直方图就是底分布;数值模拟的极值统计规定,考虑到计算代价高,这里不比较.根据文献[4]的研究结论,不同加载长度的结构效应,受车辆荷载加载的影响不同,而可能呈现差异性的底分布形状(短加载长度受重车影响大,长加载长度受加载区域内平均荷载水平控制),这里分别考察典型的短加载及长加载跨径,20m和1 000m虚拟简支梁桥,在28d实测WIM数据作用下的结构响应特性.
随机变量的正态概率纸尾部拟合如图2所示,横轴是荷载响应,纵轴为概率的正态分布逆值(即可靠度指标).可知,整体数据并不严格在一条直线上,但是两组数据的尾部走势基本在一条外延直线上,说明,经验外推方法不依赖于效应的加载跨径,此外正态分布虽无法表达底分布的整体状况,但对于尾部走势估计的可信度较高,具有合理性.
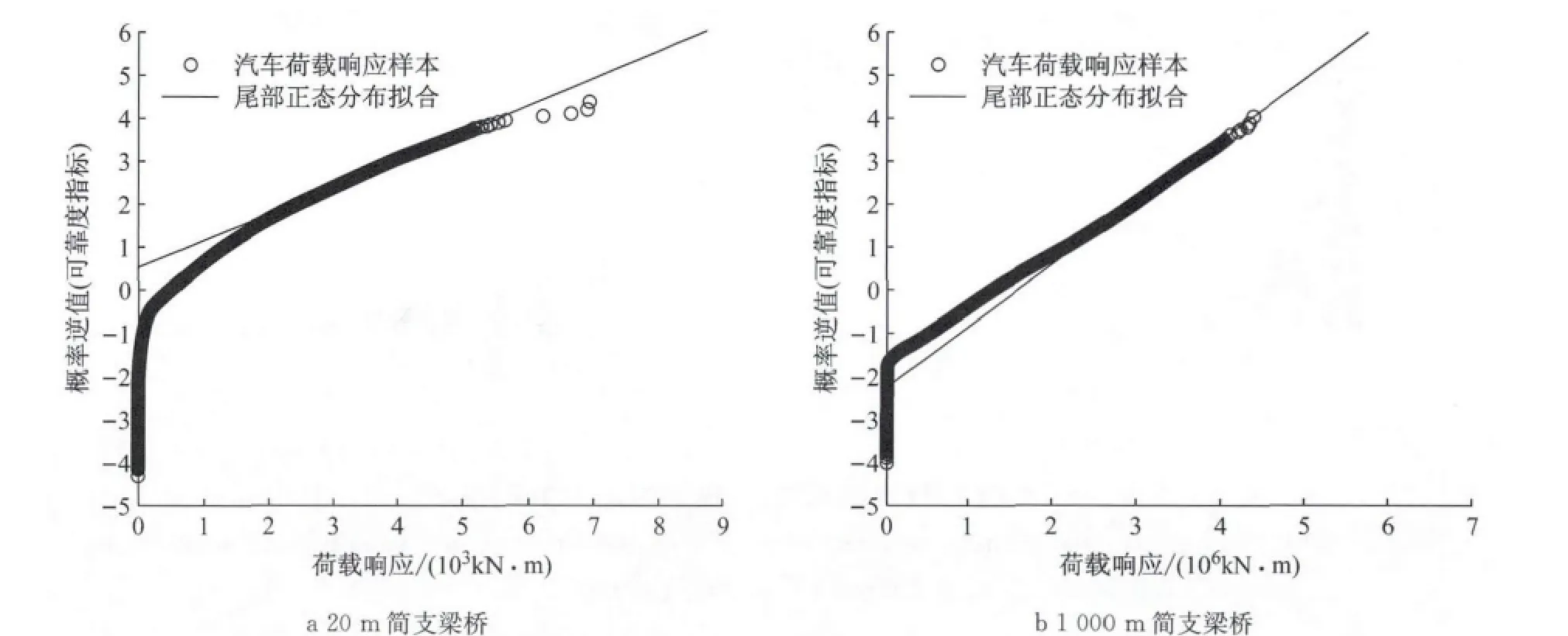
图2 不同跨径虚拟简支梁桥跨中弯矩效应的荷载响应正态分布尾部拟合Fig.2 Nail fitting of normal distributions of mid-span bending moment in simply supported bridges with different hypothetic spans
基于经典极值理论的最大值外推,采用区组最大值(选择区间为1d)构建底分布样本,对底分布进行拟合如图3所示.可知,两组数据最大值样本有限,数据零散变异性强,无法采用一种极值分布或者经验分布描述数据的特征.说明,最大值外推方法同样不依赖于效应的加载跨径,且当数据样本有限的条件下,采用最大值外推方法,获取的极值精度很难把握.

图3 不同跨径虚拟简支梁桥跨中弯矩荷载响应最大值样本拟合Fig.3 Sample fitting of maximum value of mid-span bending moment in simply supported bridges with different hypothetic spans
基于穿越次数的Rice公式外推,根据桥梁汽车荷载响应时程构建各点响应的穿越概率直方图,选择最优起点进行Rice公式拟合如图4所示.可知,随着跨径的增大Rice公式拟合的准确性越来越差,直接导致外推极值的精度降低.说明,Rice公式拟合穿越概率直方图,并不能应用于所有长加载效应的荷载响应计算中,不仅是拟合起点、区间、优度检验方法的优化,寻找合适经验分布拟合穿越概率直方图尾部走势,也至关重要.
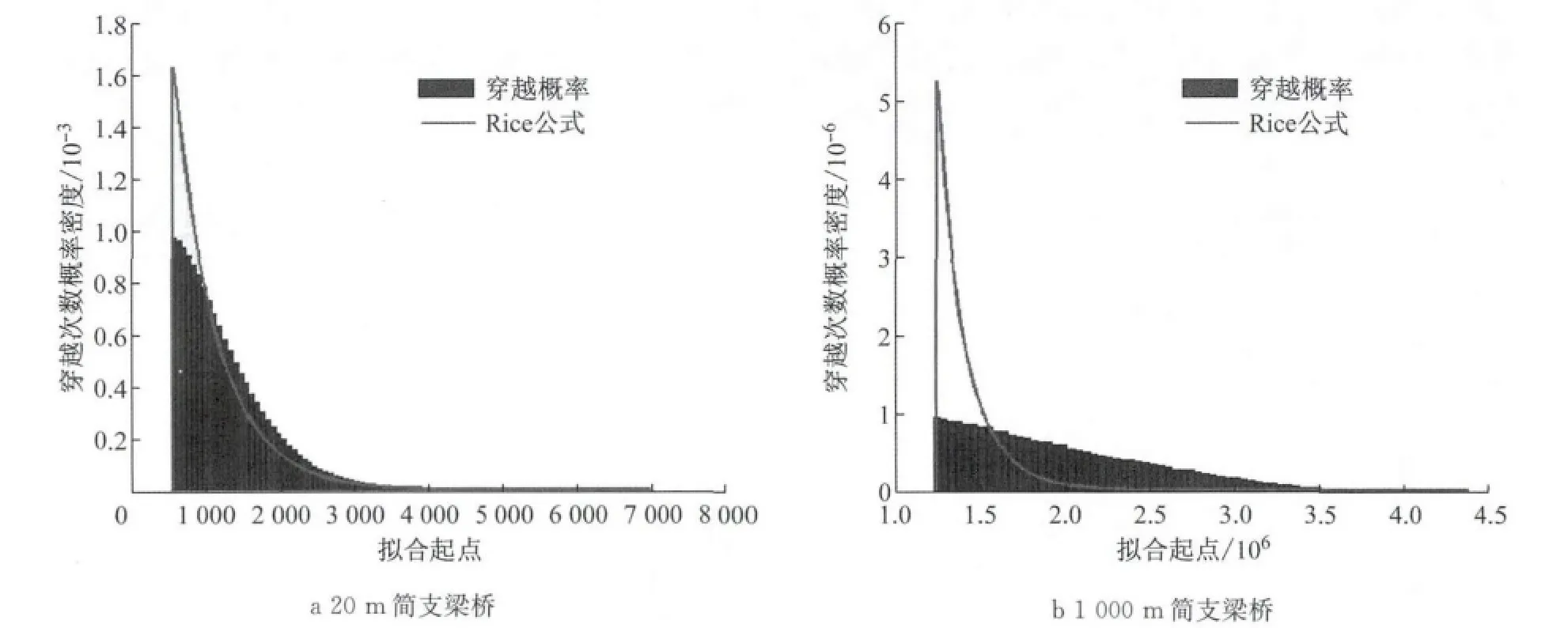
图4 不同跨径虚拟简支梁桥跨中弯矩荷载响应穿越次数概率图Rice公式拟合Fig.4 Rice Formula fitting of the probability of level crossing times of mid-span bending moment in simply supported bridges with different hypothetic spans
综上,底分布的拟合是影响外推极值的另一重要因素.对于经验假定外推,需要确定应该选择多少数据量以兼顾数据利用效率和直线外推准确性问题;对于最大值外推,则需要扩展或者测取尽可能多的数据样本以支持外推;对于穿越次数Rice公式外推,已经不仅仅是寻找最优拟合起点、区间、优度检验方法,关于适宜的经验分布描述穿越次数直方图尾部走势,也极其重要.
3 极值外推方法的比较研究
比较研究目前桥梁汽车荷载响应的主要极值外推方法,考虑到数值模拟方法的计算代价很高,穿越次数Rice公式对长加载效应外推准确性差,这里比较分析拟合经验外推和最大值外推方法.拟合经验外推比较Nowak、Moses、Sivakumar等方法,考虑到最大值外推方法与拟合经验外推方法的可靠度标准取法不一致(第1.1和1.2节),简单地统一可靠度标准会影响外推的过程,这里分开研究.
以28d高速公路四车道实测WIM数据为基础,各经验外推方法的比较如图5所示,横坐标是设计基准期,纵坐标是预测极值与我国规范D60计算值比较.可知,响应极值随设计基准期增加;三种外推方法之间Nowak方法预测极值显著大于Sivakumar方法和Moses方法;100年设计基准期的预测极值,要高于我国规范计算值;此外,荷载响应极值随着跨径的增加,与规范的比值降低,但仍然大于1.这三种经验外推方法均将可靠度指标表达为基础数据容量的关系,导致可靠度标准不统一,外推效率很高,但是精度各异,需要寻找统一的可靠度标准,以支持快速外推.
最大值外推要求基础数据样本具有较大容量,这里以28d四车道 WIM数据为基础,采用文献[29]中合成车流方法,生成时长1年的荷载数据(数据的统计特征参量与实测28d数据一致),对结构加载计算荷载响应.同样取区组(1d)最大值作为基础样本,进行最大值外推,假定1年只观测1d[11],获取不同加载跨径的响应极值见表1.表1中最大值外推极值与D60计算比值和图5外推极值与D60规范计算比值,可作为两种外推方法比较的参考,但是相互之间因为可靠度标准不一,其数值没有可比性.
表中分别对比了28d实测数据和1年合成车流作为基础样本,进行最大值外推的结果(其中1950年重现期就是目前规范荷载取值可靠度标准).可知,28d基础数据的极值外推结果离散性大,随着加载跨径增加,荷载响应外推极值与规范计算比值没有一致规律;1年合成车流外推极值与规范计算比值,随加载跨径呈现显著的降低规律,而且对于千米级加载跨径的荷载响应,比值仅为0.78,说明现有规范对于短加载跨径可能不安全,对长加载跨径偏保守,与文献[30-31]结果一致.综上,在数据样本量小的情况下,采用最大值外推精度低,外推极值离散性很大;当数据样本多时,最大值外推的精度和外推效率都较好.因此采用最大值外推,需重点解决基础数据样本容量问题,样本量有限时,不建议采用该方法.

图5 不同经验外推方法的极值特性比较Fig.5 Comparison on extreme value properties obtained by different empirical extrapolation methods

表1 荷载效应不同时长样本的最大值外推Tab.1 Maximum extrapolation of traffic load responses based on samples with different time lengths
4 结论
论文对目前桥梁汽车荷载响应的极值外推方法进行了综述,介绍了4种主要的外推方法,并对影响外推极值的关键参数:基础数据和底分布进行了研究分析,重点比较了经验外推方法和最大值外推方法,提出汽车荷载响应极值外推的发展方向.
(1)极值外推在桥梁汽车荷载中应用,主要是解决短时量测数据预测长回归周期荷载响应极值问题,预测的精度在于是否能准确描述底分布尾部数据走势.
(2)条件允许情况下,应该至少选择21d以上实测车辆数据作为荷载响应极值外推基础,才能较为准确反应荷载响应的基本统计特征.
(3)底分布对外推极值影响很大,假定拟合经验外推需重点描述底分布尾端数据走势,此时需解决高端尾部数据量选择问题;最大值外推方法受限于基础数据容量,从而影响最大值分布的拟合;穿越次数Rice公式对于不同加载长度荷载响应,不能准确描述穿越次数直方图尾部走势,除了考虑最佳拟合起点、区间和优度检验方法,经验分布的选择也至关重要.
(4)比较研究表明,经验极值外推方法具有一定可信度,但需解决可靠度统一问题;最大值外推效率和精度很高,但是需要较大的数据样本,样本量小时,外推极值的准确性较差,不建议采用.
[1] O'Brien E J,Znidaric A,Ojio T.Bridge weigh-in-motionlatest developments and applications worldwide[C]∥Proceedings of the International Conference on Heavy Vehicles.Paris:John Wiley,2008:39-56.
[2] Getachew A,O'Brien E J.Simplified site-specific traffic load models for bridge assessment[J].Structure and Infrastructure Engineering,2007,3(4):303.
[3] O'Connor A,Eichinger E M.Site-specific traffic load modeling for bridge assessment[J].ICE-Bridge Engineering,2007,160(4):185.
[4] 周军勇.大跨径多塔缆索承重桥汽车荷载模型研究[D].上海:同济大学.2014.ZHOU Junyong.Traffic load model for long span multi-pylon cable supported bridges[D].Shanghai:Tongji University.2014.
[5] O'Brien E J,Enright B,Getachew A.Importance of the tail in truck weight modeling for bridge assessment[J].Journal of Bridge Engineering,2010,15(2):210.
[6] 史道济.实用极值统计方法[M].天津:天津科学技术出版社,2006.SHI Daoji.Practical extreme statistical method[M].Tianjin:Tianjin Science and Technology Press,2006.
[7] Nowak A S.Live load model for highway bridges [J].Structural Safety,1993,13(1):53.
[8] Nowak A S,Rakoczy P.WIM-based live load for bridges[J].KSCE Journal of Civil Engineering,2013,3(17):568.
[9] Moses F,Portersvile P A.Calibration of load factors for LRFR bridge evaluation[M].Washington D C:National Academy Press,2001.
[10] Sivakumar B,Ghosn M,Moses F.Protocols for collecting and using traffic data in bridge design[M].Washington D C:National Academy Press,2011.
[11] 公路桥梁车辆荷载研究课题组.公路桥梁车辆荷载研究[R].北京:中交公路规划设计院.1997.Research Group of Vehicle Loads Research for Highway Bridge.Vehicle loads research for highway bridge[S].Beijing:China Highway Planning and Design Institutes,1997.
[12] O'Brien E J,Hajializadeh D,Sheils E.etal.Estimation of lifetime maximum distributions of bridge traffic load effects[C]∥Proceedings of the 6th International IABMAS Conference.Stresa:Taylor &Francis,2012:1482-1488.
[13] O'Connor A,O'Brien E J.Traffic load modeling and factors influencing the accuracy of predicted extremes[J].Canadian Journal of Civil Engineering,2005,32(1):278.
[14] Caprani C C,O'Brien E J.The use of predictive likelihood to estimate the distribution of extreme bridge traffic load effect[J].Structural Safety,2010,32(2):138.
[15] Fu Gongkang,You Ji.Extrapolation for future maximum load statistics[J].Journal of Bridge Engineering,2011,16(4):527.
[16] Hajializadeh D,O'Brien E J,Enright B.etal.Probabilistic study of lifetime load effect distribution of bridges[C]∥6th International ASRANet Conference.Croydon:Dublin Institute of Technology,2012:49-56.
[17] 韩大建,杜江.工程结构作用极值分析方法研究[J].建筑科学与工程学报,2008,25(2):68.HAN Dajian,DU Jiang.Research on extreme value analysis method of actions on engineering structures[J].Journal of Architecture and Civil Engineering,2008,25(2):68.
[18] 李植淮,李春前,孙健康 等.基于GPD模型的车辆荷载效应极值估计[J].工程力学,2012,29(S1):166.LI Zhihuai,LI Chunqian,SUN Jiankang,etal.Estimation of extreme vehicle load effect based on GPD model[J].Engineering Mechanics,2012,29(S1):166.
[19] Zhou Xiaoyi.Statistical analysis of traffic loads and traffic load effects on bridges[D].Paris:University Paris-Est,2013.
[20] Rice S O.Mathematical analysis of random noise[J].Bell System Technical Journal,1945,24:52.
[21] Ditlevsen O.Traffic loads on large bridges modeled as whitenoise fields[J].Journal of Engineering Mechanics,1994,120(4):681.
[22] Ditlevsen O,Madsen H O.Stochastic vehicle-queue-load model for large bridges[J].Journal of Engineering Mechanics,1994,120(9):1829.
[23] Flint A R,Jacob B.Extreme traffic loads on road bridges and target values of their effects for code calibration[C]∥ IABSE Reports.Schweiz:John Wiley,1996:469-477.
[24] Cremona C.Optimal extrapolation of traffic load effects[J].Structural Safety,2001,23(1):31.
[25] Cremona C.Probabilistic approach for cable residual strength assessment[J].Engineering Structures,2003,25(3):377.
[26] O'Brien E J,Cantero D,Enright B,etal.Characteristic dynamic increment for extreme traffic loading events on short and medium span highway bridges [J].Engineering Structures,2010,32(12):3827.
[27] Jacob B,Feypell-De La Beauelle V.Improving truck safety:potential of weigh-in-motion technology[J].IATSS Research,2010,34(1):9.
[28] Pan Ling,Han Dajian.A study on assessment method of traffic load effect of bridge in service [C]∥2th International ISCM Symposium and the 12 th International EPMESC Conference.Washington D C:AIP Conference Proceedings,2010:1225-1230.
[29] 阮欣,周小燚,郭济.基于合成车流的桥梁车辆荷载响应极值预测[J].同济大学学报:自然科学版,2012,40(10):1458.RUAN Xin, ZHOU Xiaoyi, GUO Ji.Extreme value extrapolation for bridge vehicle load effect based on synthetic vehicle flow [J].Journal of Tongji University:Natural Science,2012,40(10):1458.
[30] 阮欣,周军勇,石雪飞.中法高速公路车流及荷载特性对比[J].同济大学学报:自然科学版,2013,41(9):1392.RUAN Xin,ZHOU Junyong,SHI Xuefei.Comparison on highway traffic flow and load properties of China and France[J].Journal of Tongji University:Natural Science,2013,41(9):1392.
[31] 阮欣,周军勇,石雪飞.随机车流作用下多塔斜拉桥总体荷载响应特性[J].同济大学学报:自然科学版,2014,42(1):25.RUAN Xin,ZHOU Junyong,SHI Xuefei.Overall vehicle load response characteristic of multi-span cable-stayed bridge under stochastic traffic flow [J].Journal of Tongji University:Natural Science,2014,42(1):25.

