基于视觉感知偏差的公路几何平纵协调性分析技术
陈雨人,余 博,贺思虹
(同济大学 道路与交通工程教育部重点实验室,上海201804)
“平纵组合不当”是产生公路危险路段的主要原因之一,平纵组合对安全的影响要远远大于单个平、竖曲线的影响,不良的线形组合会导致交通事故明显增加,一些研究者专门做过研究,比如梁夏等[1]研究发现平纵完全错开事故率是组合重合的1.61倍.事实上,平纵协调是现代公路设计中的重要内容,我国公路路线规范 (JTG D20—2006)(以下简称《规范》)对于平纵线形组合设计做出了原则性的规定,要求设计车速不小于60Km·h-1的公路几何线形要进行组合设计,尤其当平曲线半径小于2 000m,竖曲线半径小于15 000m时,组合设计显得更为重要.其核心就是要求平纵均衡,驾驶员可以正确地感知信息,避免出现较大偏差.由于《规范》只给出了原则性要求,因此国内外学者针对公路几何平纵组合的具体评价方法和分析手段都进行了广泛深入的研究,归纳起来大致可以分为:(1)基于动力学的稳定协调性评价,主要通过分析车辆在平纵组合路段复杂的受力状态及其稳定性而进行评价,比如林声等[2]、刘建蓓等[3]基于空间曲率对公路几何平纵协调性进行分析;(2)基于运行车速的评价方法,主要思路是分析车辆在平纵组合路段的运行速度,比如符锌砂等[4]通过运行车速预测模型、刘建蓓等[3]通过相邻路段运行速度差和速度梯度来评价公路几何平纵组合的协调性;(3)基于视觉的安全协调性评价,主要通过分析是否存在错视觉以及视觉连续性等评价路线平纵组合的安全性,比如潘兵宏等[5]通过动视觉原理研究在视觉上如何保持连续和流畅,提出了通过平曲线半径和纵坡的关系来考察平纵均衡情况,杨轸等[6]通过特征信息变化率对公路线形质量进行评价,认为平曲线半径越小,驾驶员获得的公路特征信息变化率就越大,魏连雨等[7]通过计算曲线所需要的视距对竖曲线和平曲线的组合情况进行评价;(4)基于经济指标评价路线平纵组合的协调性,这主要从燃油经济性方面进行的评价.
上述这些研究总体来说都各有特点,其中通过驾驶员视觉角度研究公路线形平纵组合应该是比较主流的方法,从国外研究来看也是如此,Flides和Triggs[8]认为公路透视图的形状在几何图形上更加复杂,且比平面图能提供更多的曲率信息,或者说透视图信息显示了比单纯平面或者纵断面更丰富的内容.显然,其中最为关键的是公路透视图及其中心线,它提供了绝大部分的几何信息及平纵组合情况.我国《规范》认为透视图不仅可用来判断平面线形和纵面线形以及公路和风景是否协调,而且小自超高缓和段的连接,大至构造物的设计,差不多在公路几何设计的所有领域中都可以利用.不过从目前国内外研究成果来看,应用公路透视图及中心线信息来分析平纵组合以及视觉上的连续和流畅等方面仍然比较模糊定性,在实际应用中难以操作.从数学角度来看,公路透视图中心线是由多段曲线组合而成的,随着车辆的不断运动,这些多段曲线持续在驾驶员视野中动态变化,驾驶员正是从这些不断变化的多段曲线中获得操控车辆的重要信息,产生了期望车速和其他行为.如果这些被感知的信息和公路条件所能提供的相差比较大,就容易带来诸如运行车速和设计车速不一致、心理预期和实际供给不符合等情况,产生种种紧张、不舒适和判断失误等问题.特别是平面信息感知方面更是如此,由于透视的影响,驾驶员会把平曲线感觉更平坦了或者更尖锐,Fildes和 Triggs[8]、Zakowska[9]发现驾驶员在遇到小半径或者小偏角平曲线时,则倾向于感觉到的平曲率变小.而不当的平纵组合有可能加大了视觉感知的偏差,Bidulka[10],Hassan和 Easa[11]等研究表明,平曲线与凹曲线重合时会显得更加平坦,而在与凸曲线重合时感觉更加弯曲.
因此可以认为,这里存在着一个公路对象—透视图—视觉信息感知的认知过程,驾驶员眼中的透视图主要是由公路的平纵线形结合横断面产生三维映射产生的,其核心是透视图上面的中心线,由驾驶员通过视觉感知并产生信息认知.由于平纵组合以及其他因素的影响,驾驶员获得的“感知平曲率”和“实际平曲率”之间可能会存在偏差,当这种偏差超过一定范围时,就可能会导致驾驶行为出现问题,增大交通事故发生的可能性.相反,如果驾驶员 “感知平曲率”的信息和 “实际平曲率”比较吻合,整个驾驶过程就可能是连续舒适的,此时的平纵组合设计可以被认为处于协调状态.
1 公路透视图中心线计算模型及其水平分量的计算
1.1 公路“透视图中心线”计算模型
公路透视图中心线是由一系列连续点构成的具有特定形态的线形,对其形态的描述是关键,不少学者 都 对 此 进 行 过 研 究,比 如 Brummelaar[12]和Kanellaidis[13]等观察发现,平曲线在透视图中的形态类似抛物线或者是双曲线,因此长期以来,用抛物线来描述透视图中心线是一种比较常用的分析方法,除此以外,还有“双曲线模型”、“直线-抛物线模型”、改进的“双曲线模型”、“回旋曲线模型”和“样条曲线模型”等[14].不过这些模型基本上都属于二次函数,一般只能描述存在一个拐点的中心线形态,对于描述简单平曲线形成的透视图是合适的,但如果需要描述类似S曲线、复曲线等比较复杂的形态就无能为力了.因此,根据透视图中心线特点,采用三次曲线描述更为恰当,可以将拐点增加到2个,可以满足大部分情况下公路透视图中心线形态描述的需要.从数学角度来说,三次Bezier、三次B样条和Catmull-Rom样条都是比较常用的三次曲线,无论从控制点位置和还是从曲线拟合情况来看,Catmull-Rom样条曲线都要明显比其他两种样条曲线更适合用来建立公路透视图中心线计算模型[14].
1.2 “水平分量中心线”的确定
如图 1 所示,设 (P1L、P2L、P3L、P4L)和 (P1R、P2R、P3R、P4R)分别为透视图左右边线上对应的控制点,(P12、P13、P14)分别为两直线{P1LP2L,P1RP2R}、{P1LP3L,P1RP3R}和{P1LP4L,P1RP4R}的交点,根据透视学原理,如果没有纵断面的影响,(P12、P13、P14)应该位于同一条视线消失线上,但是如果有纵断面影响以后,这些点就可能在该消失线上下移动.本文的“水平分量”中心线是指透视图中心线向视平面投影形成的中心线,可以通过计算控制点(P1,P2,P3,P4)在视平面上对应的投影点获得.设(P1,P2,P3,P4)在 视 平 面 的 投 影 点 为 (P1_H,P2_H,P3_H,P4_H),根据透视原理,P1和P1_H是同一个点,不需要专门计算.这里以计算P2的投影点P2_H为例介绍计算过程,如图1a,连接(P1L、P2L)和(P1R、P2R),并延长交于点P12,过该点向视线消失线做垂线,得到点P12_H,然后过P2点向视平面做垂线,与P1P12_H相交的交点即为P2_H.同样,先求(P1L、P3L)和(P1R、P3R)、(P1L、P4L)和(P1R、P4R)的交点,然后按照类似方法可以求出P3_H和P4_H点,其过程分别如图1b和c所示.
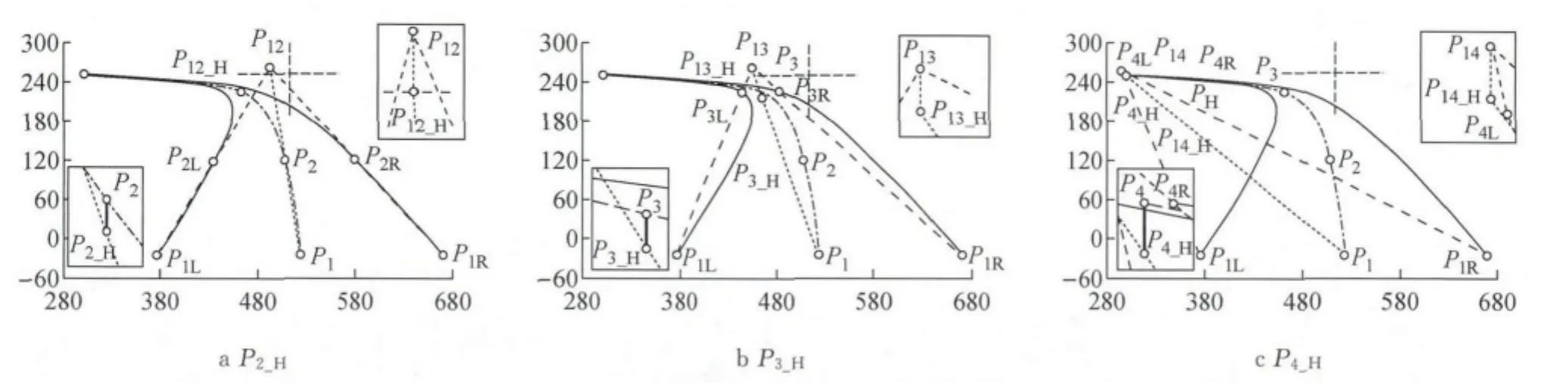
图1 透视图中心线水平分量计算方法Fig.1 A calculation method of the centerline horizontal component in the perspective view
1.3 透视图形状参数的计算
设[Vs_i(i+1),Vk_i(i+1)]和 [Ps_i(i+1),Pk_i(i+1)]分 别为表达“透视图中心线”和“水平分量中心线”在“近景”、“中景”和“远景”三个区域形态的形状参数,其中i=1,2,3,有关形状参数的计算方法可参考文献[14],这里主要介绍水平分量指数的计算.
1.4 水平视觉感知偏差分量指数的计算
所谓平纵协调,应该使得驾驶员平纵组合情况下通过透视图中心线能够对公路几何信息正确的感知,不产生比较大的偏差.事实上如果不存在纵断面影响,那么“实际感知”和“水平分量”就应该是一样的,因此这里所说的偏差就是“实际感知”和“水平分量”之间的差别.为此,采用水平视曲率分量指数来表达视觉感知偏差的情况,具体计算方法如下:
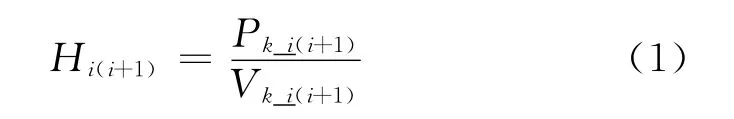
其中:i=1,2,3,Vk_i(i+1)和Pk_i(i+1)分 别 为 “近 景”、“中景”和“远景”三个区域的视曲率及其水平分量,Hi(i+1)表示视觉感知水平偏差的分量指数.
2 不同平纵组合产生视觉感知偏差规律分析
为了分析不同平纵组合所产生的视觉感知偏差的情况,根据传统的几种典型的平纵组合进行试验和计算,平面分为 “单交点曲线”、“同向曲线”和“反向曲线”三种情况,纵断面分为 “单凸曲线”、“单凹曲线”、“凸曲线+凹曲线”和“凹曲线+凸曲线”4种情况,共有12种组合方式,既包括常规的“平包竖”和“顶点对顶点”等被认为协调性好的情况,也包括“顶点对起终点”等被认为协调性最差的情况.绘制12种组合的透视图并计算形状参数和水平分量指数,其中以样本1,2,3,4,7和10为例列在表1中.
样本{1,4,7,10}平面设计完全相同,都为“单交点曲线”,纵断面设计不同,依次为“单凸曲线”、“单凹曲线”、“凸曲线+凹曲线”和“凹曲线+凸曲线”.不同的纵断面设计对相同平面的影响差别很明显,“单凸曲线”使得中心线的实际感知曲率比水平分量来得小,同时“单凹曲线”使得中心线的实际感知曲率比水平分量来得大.对应样本{1,4,7,10},“近景”水平分量指数分别为(1.01,1.15,0.91,1.28),“中景”为(0.86,1.10,0.83,1.20),而 “远景”则为(0.76,0.86,2.56,0.49),总体来说纵断面对“中景”和“远景”视觉曲率的影响是比较大的,由于不同纵断面的影响,驾驶员感知到的水平曲率会有10%~25%的变化.
样本{1,2,3}平面设计不相同,分别为“单交点曲线”、“同向曲线”和“反向曲线”,纵断面设计相同,都为“单凸曲线”.相同的纵断面设计对不同平面设计的影响差别也比较明显,对应样本{1,2,3}的“近景”的水平分量指数为(1.01,1.10,1.06),“中景”为(0.86,0.84,1.04),而“远景”则为(0.76,1.13,0.93),总体来说纵断面对“中景”和“远景”视觉曲率的影响也是比较大的.因此,对应不同的平面设计,由于纵断面设计的影响,驾驶员感知到的水平曲率会有5%~15%的变化.
上述说明,平纵组合对驾驶员视野中、远端的影响比较大,而对近处的影响比较小.此外,从数据也可以看出凹曲线成分有使驾驶员对水平曲率感知比实际大的情况,而凸曲线的成分有使驾驶员感知水平曲率比实际要小的可能,因此通过控制平纵组合可以调节驾驶员视觉感知产生的偏差.即使平面设计相同,由于纵断面的影响,完全可能产生不同的信息感知,关键相对平曲线来说,竖曲线成分的影响有多大.由此可见,公路路线几何平纵组合对驾驶员的信息感知会产生影响,但是由于透视的作用,内在的关系比较复杂,并不是一一对应的关系,因此对于公路平纵协调程度的分析,仅仅从平纵设计指标这端来分析是不完善的,应该从驾驶员视觉感知端来分析才更为可靠.

表1 不同平纵组合产生视觉感知的水平分量指数计算Tab.1 Horizontal component index calculated about different combinations of horizontal and vertical design
3 基于驾驶员视觉感知偏差的公路路线几何平纵组合分析
通过不同平纵组合产生视觉感知偏差规律分析,可以明确对于类似公路几何平纵组合设计的评价,最有效的办法就是要从驾驶员视觉感知的角度进行,这就需要解决两个方面的问题,一个是评价分类阈值的确定以及具体使用的评价方法.
3.1 基于视觉感知偏差的分类阈值的确定
本文采用区间估计方法来计算满足一定置信水平的视觉感知评价阈值的范围,取显著性水平α=0.05,则置信度=1-α=0.95.通过从总体中抽取样本,根据一定的正确度与精确度的要求,构造出适当的区间,作为总体的分布参数所在范围的估计.
使用以往已经进行过安全评价的高速公路资料作为样本,所采用的数据为从驾驶员视角拍摄的高速公路照片,样本路段涉及两段,其中一段是浙江上三高速,另一段是京沪高速临沂段,随机选择了100个存在路线几何平纵组合的作为样本,分别提取“实际感知”和“水平基准”中心线,计算相应的视觉感知偏差值,图2是相关视觉感知偏差的分布情况,概率密度函数都呈正态分布,表明视觉偏差分布服从一定的规律性,可以作为总体参数估计的样本,现在要以此为基础,估计总体视觉感知偏差的分类阈值.

图2 视觉感知水平分量指数的概率分布密度函数Fig.2 Horizontal component of visual perception index probability distribution density function
设x1,x2,…,xn是来自总体X的样本,θ是一个待估计的参数,对于给定的α((0<α<1),若能找到两个统计量θ1(x1,x2,…,xn)和θ2(x1,x2,…,xn),使得P(θ1≤θ≤θ2)=1-α,称[θ1,θ2]为参数θ置信水平为1-α的置信区间,θ1为置信下限,θ2为置信上限,1-α称为置信水平或者置信度、置信概率,表示区间估计的可靠性,越大越可靠,而α为显著性水平,越小越可靠.由于总体的σ未知,因此使用样本标准差S代替σ,建立置信区间使用的统计量是:,服从t分布.根据区间估计的定义,总体均值应该满足P(-tα/2≤T≤tα/2)=1-α,也就是,从而有,μ的置信区间为.本文选择α=0.05,n=100,查表,μα/2=1.960,获得视觉感知水平分量指数在95%置信水平下的阈值范围分别为“近景”[0.85,1.15],“中景”[0.75,1.25]和“远景”[0.6,1.4].
3.2 基于视觉感知水平分量分类阈值的评价方法
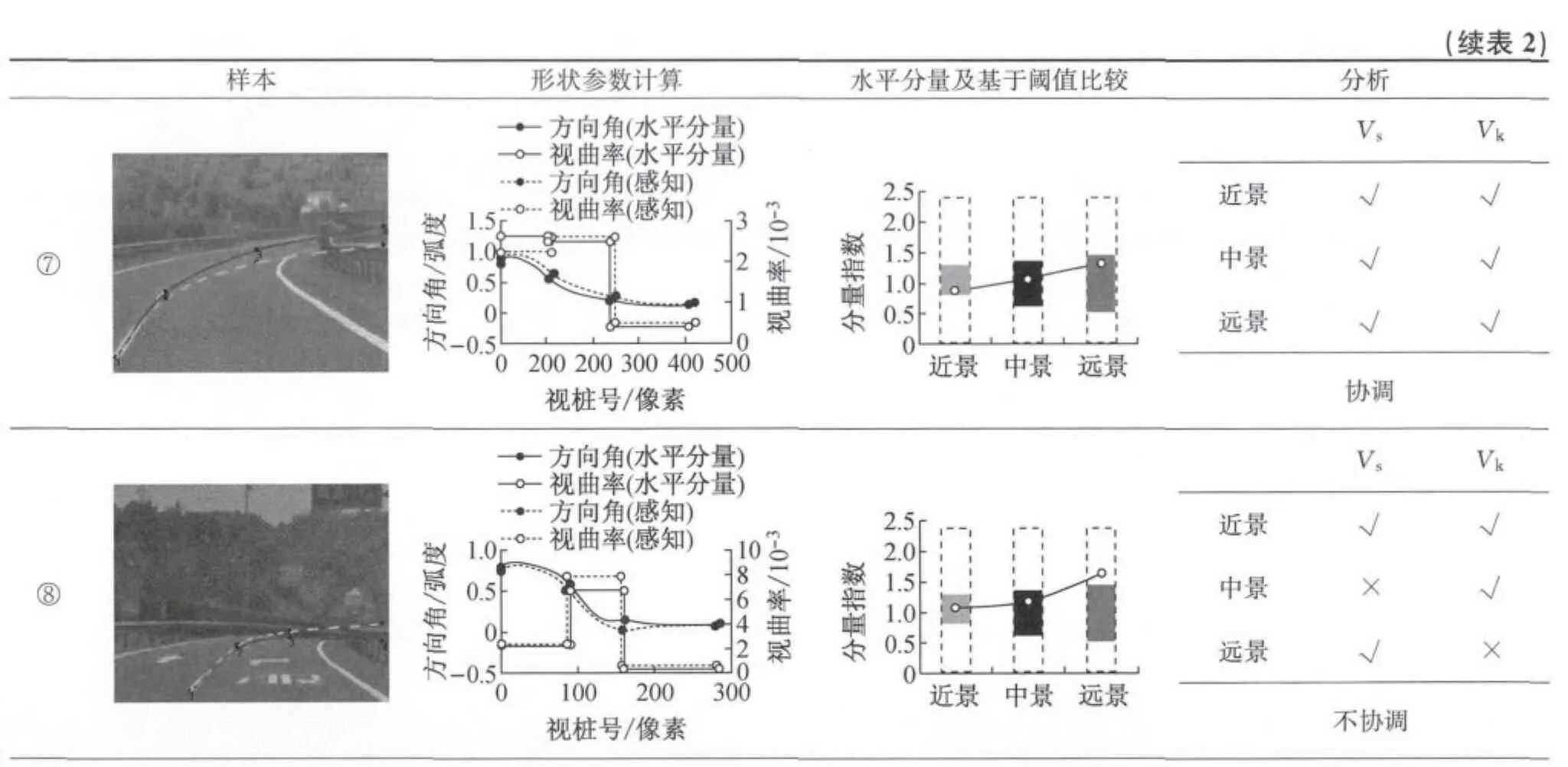
从平纵组合试验数据中选择8个在当初安全评价报告中被认为是平纵不协调的资料,应用本文研究的方法进行平纵协调性分析,见表2.表中,Vs为视曲线长,Vk为视曲率.第1列是驾驶员视角图像资料,第2列是透视图形状参数的计算,第3列是驾驶员视觉感知水平分量计算及基于分类阈值的比较,第4列是结论分析.具体评价如下:
① “近景”和“远景”的水平分量指数虽然都在阈值范围内,但是水平感知偏差较大,而且“中景”处的水平分量指数已经超过阈值范围,同时视曲线长度也不够,因此的确属于平纵组合不协调;② 通过计算发现,水平曲率的感知偏差比较大,部分已经超过阈值范围,其余虽然没超过阈值,但是已经非常接
近,因此该位置应该被认为平纵协调性差;③ “近景”、“中景”和“远景”的水平视觉感知偏差都在阈值范围内,同时视曲线长度都足够,因此该位置平纵组合是协调的;④ 水平曲率感知偏差较大,尤其是在“近景”部分,因此认为平纵组合不协调;⑤ 水平视觉感知偏差接近阈值,虽然视曲线长度满足要求,但是该位置在平纵组合方面是不协调的;⑥ 通过计算发现视距不够,尤其是“远景”部分的视曲线长度没有达到要求,虽然水平感知偏差没有超过阈值范围,带该位置平纵组合仍然属于不协调;⑦ 水平感知偏差稍大,但是并没有超出评价阈值范围,因此该位置平纵组合是协调的;⑧ “远景”部分水平感知偏差比较大,已经超过阈值范围了,所以该位置的平纵协调性差.

表2 应用案例分析Tab.2 Case study
?
4 结语
本文目的是寻找更加有效和可靠的平纵协调的评价技术,能够切实满足目前公路安全评价和致因分析的技术要求,能够把真正平纵协调不理想的位置寻找出来并加以改进,提高公路交通的安全性和舒适性.另一方面本文也期望由此深入,通过视觉感知偏差控制的计算和分析,为平纵组合设计提供参考,使得公路几何设计更加符合使用者的需求.本文评价方法中基于CatMull_Rom曲线的透视图视觉模型和视觉感知偏差的计算是关键,对评价阈值的确定采用了数理统计的方法,在今后的工作中,还需要对评价阈值进行更为细致准确的标定,这实际应该是一个不断完善的过程.
[1] 梁夏,郭忠印,方守恩.道路线形与道路安全性关系的统计分析[J].同济大学学报:自然科学版,2002,30(2):203.LIANG Xia,GUO Zhongyin,FANG Shouen,Statistic analyses of relations between road alignment and road safety[J].Journal of Tongji University:Natural Science,2002,30(2):203.
[2] 林声,郭忠印,周小焕,等.公路线形空间几何特性模型及其应用[J].中国公路学报,2010,23(增刊):47.LIN Sheng,GUO Zhongyin,ZHOU Xiaohuan,etal.Models of highway alignment spatial geometric properties and their applications[J].China Journal of Highway and Transport,2010,23(Supplement):47.
[3] 刘建蓓,郭忠印,胡江碧,等.公路路线设计安全性评价方法与标准[J].中国公路学报,2010,23(增刊):28.LIU Jianpei,GUO Zhongyin,HU Jiangbi,etal.Safety evaluation method and standard of highway alignment design[J].China Journal of Highway and Transport,2010,23(Supplement):28.
[4] 符锌砂,刘 震.基于平纵组合线形的理论运行速度预测模型[J].长安大学学报:自然科学版,2010,30(3):24.FU Xinsha, LIU Zhen.Prediction model of theoretical operating speed based on combination alignment of cross and vertical section[J].Journal of Chang an University:Natural Science,2010,30(3):24.
[5] 潘兵宏,赵一飞,梁孝忠.动视觉原理在公路线形设计中的应用[J].长安大学学报:自然科学版,2004,24(6):20.PAN Binghong,ZHAO Yifei,LIANG Xiaozhong,Application of dynamic vision theory in highway alignment design[J].Journal of Chang an University:Natural Science,2004,24(6):20.
[6] 杨轸,潘晓东,方守恩,等.基于道路特征信息变化率的公路线形质量评价[J].公路交通科技,2006,23(10):1.YANG Zhen,PAN Xiaodong,FANG Shouen,etal.Highway alignment evaluation based on road characteristic information variation[J].Journal of Highway and Transportation Research and Development,2006,23(10):1.
[7] 魏连雨,杨春风,崔洪军,等.竖凸曲线与平曲线组合设计的新方法[J].中国公路学报,2002,15(1):15.WEI Lianyu,YANG Chunfeng,CUI Hongjun,etal.A new design method to achieve the coordination of crest and horizontal curve[J].China Journal of Highway and Transport,2002,15(1):15.
[8] Flides B N,Triggs T J.The Effects of road curve geometry and approach distance on judgements of curve exit angle[J].Journal of Transportation Engineering,1982,11(4):135.
[9] Zakowska L.Road curve evaluation based on road view perception study[J].Transportation Research Record,Journal of the Transportation Research Board,1999,1689(1):68.
[10] Bidulka S,Sayed T,Hassan Y.Influence of vertical alignment on horizontal curve perception:phase I:examining the hypothesis[J].Transportation Research Record,Journal of the Transportation Research Board,2002,1796(1):12.
[11] Hassan Y,Easa S M.Effect of vertical alignment on driver perception of horizontal curves [J].ASCE Journal of Transportation Engineering,2003,129(4):399.
[12] Brummelaar T.The reversal point in the perspective road picture[J].Australian Road Research,1983,13(2):123.
[13] Taiganidis I,Kanellaidis G.Approximate perspective design of roads[J].Journal of Transportation Engineering,1999,125(4):314.
[14] 陈雨人,王瑞云、董永杰,等.应用CatMull-Rom样条曲线描述道路透视图中心线特征的方法研究[J],重庆交通大学学报:自然科学版,2015,34(4):48.CHEN Yuren,WANG Ruiyun,DONG Yongjie,etal.Methods about using CatMull-Rom spline to describe characteristics of road centerline in perspective view[J].Journal of Chongqing Jiaotong University:Natural Science,2015,34(4):48.

