钢筋混凝土高墩多水准抗震性能试验
管仲国,李晓波,李建中
(同济大学 土木防灾国家重点实验室,上海200092)
在过去的20年里,中国在西部山区己建成十余座百米以上墩高的高墩桥梁,其中陕西咸(阳)旬(邑)高速公路三水河特大桥最大墩高达183.5m[1].高墩由于结构较柔,一般具有较长振动周期,可以避开地震的卓越能量频段,同时高墩的变形能力较大,因此在防倒塌、保障生命安全上具有较好的保障[2].但在强震作用下损伤是难以避免的,而高墩桥梁的损伤修复要比普通桥梁困难得多.2008年汶川地震中,都汶高速公路庙子坪岷江特大桥5号主墩墩底部位产生两道贯通性裂缝,最大裂缝宽度0.8mm.由于主墩墩高102.47m,入水深度70余米,给震后修复带来了很大困难,最终采用钢沉箱进行加固,并聘请专业的潜水员辅助施工,整个修复过程历时近1年,耗资巨大[3].同时,高墩桥梁一般都位于关键的枢纽地位,一旦发生震害,所导致的直接、间接经济损失也要大得多.由此可见,高墩桥梁的抗震设计应以早期损伤控制为主.然而,目前对桥梁墩柱的抗震性能试验研究较多都是关注其极限延性能力,而对早期损伤状态的研究则较少.
本文对4个箱形截面柱模型进行了拟静力试验,研究了滞回性能、残余裂缝、混凝土压碎与剥落、以及极限破坏等多水准性能状态.
1 试验概况
1.1 试件设计
试件设计以云南昆石公路上的一座高墩桥梁为基础,模型和原型之间采用相同的断面纵筋配筋率和轴压比,其中纵筋直径为12mm,配筋率为1.93%,设计轴压比为0.1.共包括4个悬臂墩试件,主要试件设计参数见表1.由于高墩结构一般采用箱型断面,试验模型也采用箱形断面形式,同时为加工方便,各试件均采用等截面B·W(宽×高)为600 mm×768mm,如图1所示.试件的变化参数包括墩高和配箍率,其中墩高L为4.0~4.6m;体积配箍率为0.42%~1.18%,保持箍筋间距不变,分别采用直径为6,8和10mm的光圆钢筋.
材性试验结果:折算混凝土抗压强度标准值为43.5MPa;主筋屈服强度为340MPa,极限强度为512MPa.
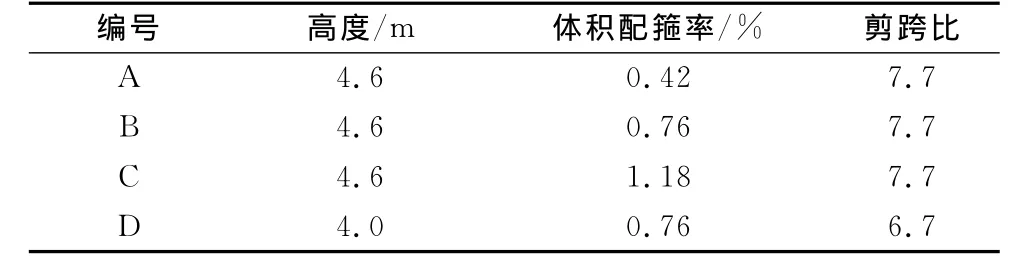
表1 试件主要设计参数Tab.1 Detail parameters of specimens
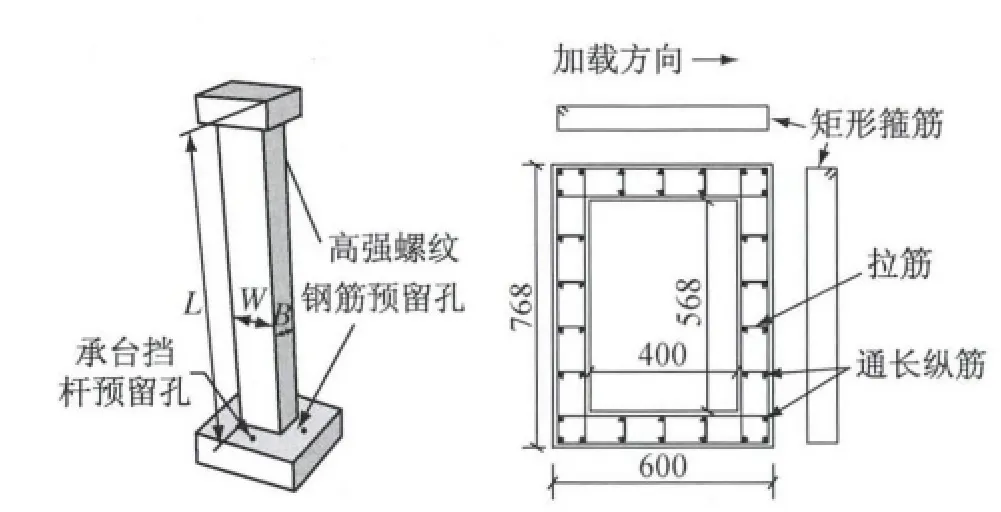
图1 试件构造示意与截面配筋方案Fig.1 Dimension and reinforcement details
1.2 加载装置与加载制度
墩柱加载模式为典型的悬臂墩加载,具体加载装置如图2所示.墩底由锚栓将墩底承台固定于地板上;竖向荷载由墩柱两侧的锚固拉杆和1 000kN穿心千斤顶提供,保持总轴力626kN;水平加载系统由水平反力墙和德国SHENK公司生产的630 kN电液伺服高性能作动器提供,位移行程±250 mm.
加载过程中,弹性阶段采用荷载控制的方式,以40%、60%和80%的屈服荷载加载三个等级.此后采用位移控制加载,主要以偏移率为控制指标.为了较好地观测早期的裂缝发展状况,当残余裂缝宽度小于0.6mm时,位移加载的步长采用0.1%偏移率,大于0.6mm时,步长0.3%偏移率,每一个加载等级均施加3个循环.
1.3 量测内容
如前言部分所述,本次研究的重点内容为高墩结构的多水准抗震性能,因此试验过程中,除了滞回性能以外,还重点观测了早期损伤中裂缝的发展过程,监测裂缝宽度的发展历程.当裂缝出现后,选取最大裂缝位置并用裂缝显微镜测量其宽度,跨越裂缝安装夹式引伸计(Epsilon Model 3541,测量精度0.005mm),如图3所示,并记录引伸计的初始值.如此,裂缝宽度的变化就可以由引伸计的张开位移来获得.此外,试验过程中还采用裂缝显微镜对裂缝宽度进行观测,以便与引伸计的量测结果进行比对和验证.
2 试验结果分析与多水准性能控制
现有的混凝土结构多水准性能,往往采用轻微、中等、严重、倒塌等程度性副词进行描述,彼此间的界限相对较为模糊.从实际震害上看,结构更直观的表现是损伤状态.为此,本文基于试验研究,更多地从直观的损伤状态以及所对应的修复需要,来区分不同的性能等级.

图2 加载装置Fig.2 Testing setup
2.1 滞回曲线
墩顶水平荷载滞回曲线如图4所示,其中偏移量为墩顶水平位移与墩高的比.由于试验中的竖向荷载是采用锚固拉杆施加的,图4在数据处理中,通过扣除锚杆拉力的水平分力对水平荷载进行了修正.此外,试件B由于在加载后期发生了竖向拉杆锚固端螺栓滑丝破坏,此后改为无轴力加载.从图中可以看出,高墩构件由于主要以受弯为主,滞回曲线较为平滑饱满,此外,随着配筋率的提高,屈服后承载力的下降趋势也逐渐变缓.
基于Opensees平台,采用纤维模型梁法进行了数值模拟.其中,混凝土本构关系采用Kent-Park模型,钢筋采用考虑屈服-强化的Chang-Mander模型,此外,还考虑了柱底纵筋在基座中的屈服渗透效应[4].从图中对比可以看出,数值模拟与试验结果符合较好,这表明采用纤维模型可以较好地模拟高墩结构的滞回性能.

图3 引伸计测量示意Fig.3 Clip gage and the schematic diagram for measuring

图4 滞回曲线Fig.4 Hysteretic curves
2.2 残余裂缝
一般认为钢筋混凝土结构是带裂缝工作的.对于不同的环境条件,当裂缝宽度小于某一限值(一般为0.1~0.3mm)时,并不会对结构的耐久性产生明显不利影响.以此类推,若震后某一结构承载能力基本没有损失,仅发生了较小的残余裂缝损伤,则可以不对其进行任何加固.而当残余裂缝宽度超过限值时,即使结构的承载力无明显损失,仍需进行耐久性加固.由此可见,残余裂缝宽度实际上是决定结构中是否需要进行耐久性加固的一个重要指标.然而,目前对于残余裂缝的研究非常少,尤其是试验研究.其中的一个原因就是拟静力试验当屈服发生以后一般应采用位移控制加载,而这一过程不便于在荷载零点进行裂缝观测.Lehman[5]、Calderone[6]等对开裂行为的研究也都是在试件完全回到位移零点时进行的.由于在实际地震中,当动力作用消失后,结构将静止在其内力平衡位置上,而不是回到位移零点,因此这种完全复位的状态是难以实现的.
本次试验中通过夹式引伸计对裂缝宽度进行了全过程监视,进而对残余裂缝进行了重点研究.4个试件在试验过程中的开裂状态与裂缝发展基本相似.当荷载等级达到60%名义屈服荷载时,距墩底0.11H~0.13H(H为计算墩高)范围内可见三道裂缝,其中,墩高较矮的D试件,裂缝平均间距150 mm左右,墩高较高的A、B、C试件,平均间距200 mm左右,卸载后均可完全闭合,表明结构仍处于弹性状态;当位移加载幅值达到0.8%~1.0%偏移率时,残余裂缝开始出现,宽度约为0.01~0.02mm,此时选取最大裂缝位置,安装引伸计并监测其发展.
图5所示为D试件的裂缝宽度分别与加载位移和水平力的滞回关系.从图中可以看出:裂缝宽度随位移和荷载的变化关系有很大的差异,随荷载变化的非线性表现更强,滞回特征也更为明显.但在同一加载等级下,三次重复加载,裂缝变化路径基本相同.这表明,裂缝宽度的增加主要受加载位移幅值的大小影响,同一等级下的重复加载对裂缝宽度的影响较小,其他试件的规律与之相似.Leman在试验中也观察到了类似的现象.图6以试件A为例,给出最大裂缝、对应卸载至荷载零点和重新回到位移零点时的裂缝宽度对比.可以看出,引伸计的观测结果与裂缝显微镜基本一致.此外,对应卸载荷载零点时的裂缝宽度要明显大于位移复位时的裂缝宽度.由此可见,采用位移复位后的裂缝宽度将会严重低估实际震害中的残余裂缝损伤.
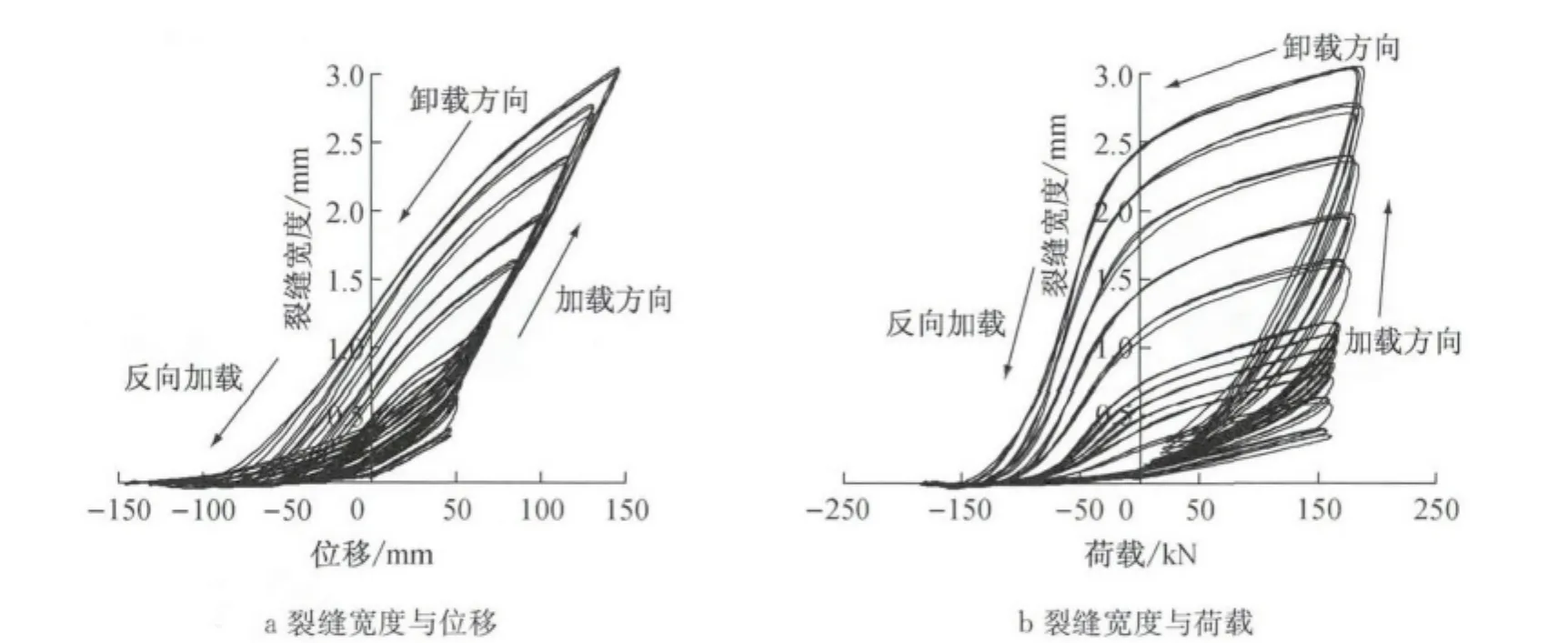
图5 裂缝宽度变化Fig.5 Progression of crack width

图6 不同状态下裂缝宽度对比Fig.6 Comparison of different crack widths
由于当动力作用消失以后,结构将重新静止在新的荷载平衡位置上,因此相比之下,采用卸载至荷载零点时刻的裂缝宽度作为残余裂缝估计更为合理.此外,相关研究表明,从统计意义上看,结构在地震中的塑性变形绝大部分会以永久变形的形式保留下来,而拟静力试验中卸载至荷载零点意味着全部的塑性变形均得到保存,因此采用这个估计,结果也将更加偏于安全[7-8].

图7 残余裂缝与塑性角位移Fig.7 Residual crack width vs.plastic rotation
残余裂缝的大小,在一定程度上也反映了塑性铰区永久塑性变形的大小.图7给出了残余裂缝宽度与墩底塑性角位移之间的关系,其中,残余裂缝和塑性角位移均取卸载至荷载零点时的值.可以看出,两者之间总体上呈现线性关系.这意味着,对残余裂缝的控制可以间接通过控制塑性铰塑性变形的大小来实现.
考虑到数据结果的离散性.式(1)按90%保证率给出了残余裂缝宽度wR的偏上限估算:
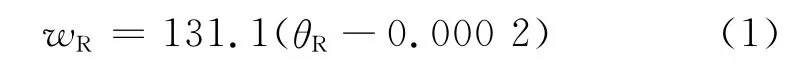
式中,θR为塑性角位移.
由此可见,若性能设计中能允许发生0.1~0.3 mm的残余裂缝宽度,由式(1)可知,此时按90%保证率的塑性角位移偏下限值约为0.001~0.002 5,即0.1%~0.25%的残余位移,此时所对应的位移延性系数约为1.12~1.31,这表明容许一定的残余裂缝损伤、但并不需要进行任何加固,则可比完全基于强度设计多出10%~30%的强度折减空间.需要指出的是,影响混凝土结构裂缝宽度的因素还有很多,即使是对应相同的裂缝宽度,影响其耐久性的因素也很复杂,对此还应开展更广泛的研究.
2.3 混凝土压溃与剥落
混凝土压溃是墩柱损伤状态的另一个重要界限标志.在此之前,除刚度以外,原结构的完整性和承载能力均基本保持,可能的修复工作也主要是裂缝注浆和封闭等耐久性加固措施;而在此之后,由于混凝土完整性受到破坏,结构刚度下降较大,甚至结构承载力也受到削弱,需要更多的结构性加固措施,如混凝土补强、钢筋调直等,而对于发生混凝土保护层严重剥落、纵筋屈曲的情况,则还要根据情况进行纵筋补强,甚至是整个塑性铰区补强加固等.
图8a和8b所示分别为本次试验中发生混凝土压溃(剥落发生的前一级)和严重剥落时的破坏特征.表2所示为各试件对应混凝土发生压溃和剥落时所对应最大墩顶偏移率和塑性铰区最大角位移.可以看出,不同配箍率对混凝土压溃时的偏移率几乎没有影响,对混凝土剥落的影响也仅在10%左右.平均而言,对应混凝土压溃时的最大偏移率为2.39%;对应混凝土剥落时的最大偏移率为3.36%.

图8 混凝土压溃与剥落Fig.8 Concrete crushing and spalling
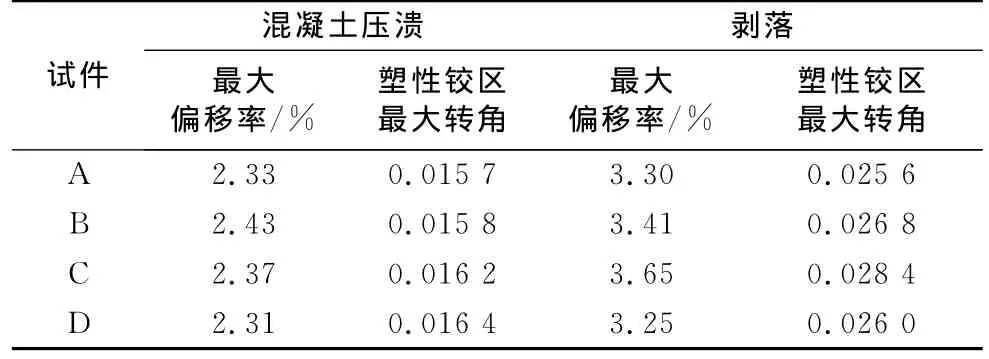
表2 混凝土压溃与严重剥落下的特征位移Tab.2 Characteristc deformations on concrete crushing and spalling
表3统计了美国太平洋地震工程中心(PEER)的混凝土柱试验数据库[9],以及宋晓东[10]共计24个矩形截面悬臂墩的试验结果,其中轴压比的变化范围为0.05~0.25.总体上,对应混凝土压溃时的偏移率分布较为集中,均值0.024,标准差0.005,与本次试验结果的符合较好.对于明显剥落状况,由于不同观察者的判别标准差异较大,故未作统计.
2.4 极限状态
目前,对于墩柱的极限状态已开展了较多的研究.其中对极限变形能力的预测算法,较为普遍采用的是Priestley和park等[11]建议的等效塑性铰方法.该方法假定柱底的塑性曲率在一个等效塑性铰长度内均匀分布,再通过试验回归得到等效塑性铰长度的计算公式.
迄今为止,有关等效塑性铰长度Lp的计算公式有很多,其中Priestley[12]在1992年所建议的公式应用较为广泛,并已被美国国家高速公路与交通运输协会标准(AASHTO)和中国规范中采用[12],具体如下:
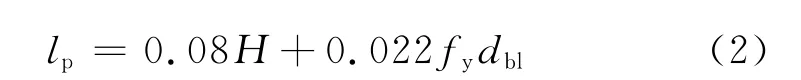
式中:H为悬臂墩墩高或者塑性铰截面到反弯点的距离;fy为纵筋屈服强度;dbl为纵筋直径.

表3 矩形柱试件统计数据[9]Tab.3 Statistic data for cantilever columns with rectangular sections[9]
2008年,Berry等[13]指出用(f′c为混凝土圆柱体抗压强度)替换fydbl能更好地考虑纵筋的屈服渗透效应,并根据37个选自PEER数据库中的墩柱试验数据,重新回归得到了新的等效塑性铰长度计算公式:

本次试验中,试件C因加载装置已达到极限位移能力未发生破坏,其余各试件的破坏状态均为纵筋屈曲后发生断裂.表3所示为各试件发生极限破坏时墩顶偏移率试验值和基于式(2)和式(3)的预测值的对比.可以看出,Priestley公式[12]的预测结果偏差较大,最大可达一倍以上.相比之下,Berry公式[13]与试验结果的符合性相对较好.事实上,在宋晓东的高墩试验中,也发现了类似的现象,即按Priestley公式法的预测结果要比试验结果大一倍左右.Priestley公式主要关注的还是普通墩柱,与墩高相关的回归系数取0.08,而Berry的样本中,约20%的墩柱具有6以上的长细比,与墩高相关的回归系数取0.05.

表3 极限状态下的偏移率Tab.3 drift ratios on ultimate state %
3 结论
基于4个高墩模型,进行了拟静力试验,重点研究了残余裂缝宽度、混凝土压溃与剥落、以及极限破坏状态等,主要结论如下:
(1)高墩构件滞回曲线平滑饱满,随着配筋率的提高,屈服后承载力的下降趋势逐渐变缓;
(2)对应位移零点时的裂缝宽度要远小于对应荷载零点时的裂缝宽度,采用位移零点时的裂缝宽度会严重低估结构的残余裂缝响应;
(3)对应荷载零点时残余裂缝宽度与塑性角位移呈线性对应关系,允许高墩结构产生0.1~0.3mm的残余裂缝,相比完全弹性反应,可有10%~30%的强度折减空间;
(4)在低轴压比条件下,对应混凝土压溃时的墩柱最大变形样本分布相对较为集中,对应的最大偏移率约为2.39%;
(5)高墩构件极限状态下的等效塑性铰长度与Berry公式的符合性相对较好.
[1] 卢皓.非规则高墩桥梁抗震性能分析方法与试验研究[D].上海:同济大学,2013.LU Hao.Analysis method and experimental study on seismic performance of irregular girder bridges with high piers[D].Shanghai:Tongji University,2013.
[2] 李建中,宋晓东,范立础.桥梁高墩位移延性能力的探讨[J].地震工程与工程振动,2005,25(1):43.LI Jianzhong,Song Xiaodong,Fan Lichu.Investigation for displacement ductility capacity of tall piers [J].Earthquake Engineering and Engineering Vibration,2005,25(1):43.
[3] 黄显彬,杨虹,恩文海,等.都汶高速公路庙子坪岷江特大桥震后5号主墩加固技术[J].建筑技术,2010,41(2):136.HUANG Xianbin,YANG Hong,EN Wenhai,etal.Du Wen expressway miaoziping minjiang river bridge after earthquake main pier on the 5th reinforcement technology [J].Architecture Technology,2010,41(2):136.
[4] Zhao J,Sritharam S.Modeling of strain penetration effects in fiber-based analysis of reinforced concrete strunctures [J].ACI Structural Journal,2007,104(S14):133.
[5] Lehman D, Moehle J, Mahin S,etal.Experimental evaluation of the seismic performance of reinforced concrete bridge columns[J].Journal of Structural Engineering,2004,130(6):869.
[6] Calderone A J,Lehman D,Moehle J.Behavior of reinforced concrete bridge columns having varying aspect ratios and varying lengths of confinement[R].Berkeley:University of California,2000.
[7] Japan Road Association.Specifications for highway bridges,Part V,Seismic Design[S].[S.l.]:Japan Road Association,2002.
[8] Lee W K,Billington S L.Modeling residual displacements of concrete bridge columns under earthquake loads using fiber elements[J].Journal of Bridge Engineering,2010,15(3):240.
[9] Berry M, Parish M, Eberhard M.PEER structural performance database user's manual[R/OL].[2004-12-31].Berkeley:University of California,http://nisee.berkeley.edu/spd.
[10] 宋晓东.桥梁高墩延性抗震性能的理论与试验研究[D].上海:同济大学,2004.SONG Xiaodong.Study on ductile seismic capacity of tall bridge piers in test and theory [D].Shanghai:Tongji University,2004.
[11] Park R,Pristley M J N,Gill W D.Ductility of square confined concrete columns [J].Journal of Structural Division,1982,108(ST4):929.
[12] Paulay T,Pristley M J N.Seismic design of reinforced concrete and masonry buildings[M].New York:John Wiley &Sons,Inc.,1992.
[13] Berry M,Lehman D,Lowes L.Lumped-plasticity models for performance simulation of bridge columns[J].ACI Structural Journal,2008,105(3):270.

