刍议小学高年级数学教学中读图能力的培养策略

[摘 要] 图形，是数学信息的重要载体；教学中要培养学生直接从图中搜集、分析和处理信息的能力，即培养读图能力. 小学高年级数学教学中，所接触的线段图、几何图形、坐标图等图象较抽象，条件隐蔽，关系复杂. 可以采用“图文结合，化零为整”，“图绘结合，化静为动”，“图型结合，化虚为实”，“图策结合，化难为易”等策略，有效培养和提升学生的读图能力.

[关键词] 小学数学；读图能力；培养策略图形，是数学信息的重要载体；《数学课程标准》指出：“要培养学生直接从图中搜集、分析和处理信息的能力”，强调读图能力的培养.小学数学低、中年级常常用直观、趣味性强的图形、图象呈现数学信息，学生已经初步学会读图，具备了初步的读图、析图能力. 高年级教学中，接触到的图象有情景主题图，更多的是线段图、几何图形、坐标图等，这些图象往往更为抽象、条件更为隐蔽，关系更为复杂. 如何进行读图能力的有效培养，提高分析和解决问题的能力，是小学高年级数学教学中亟待解决的问题. 笔者拟从“四个结合，实现四化”入手，谈谈个人的体会.

图文结合，化零为整

高年级的教材中，大量存在情景主题图、图文信息题，它们的信息较为零散. 这类题目，旨在让学生运用观察、阅读、归纳、分析的方法，获取有用的信息，以进行演算和推理，培养学生获取信息的能力、信息转化能力和应用信息的能力. 图文结合，就是要把图形和文字的信息进行综合、叠加，化零为整，又要把图文信息相互对应，将它们所蕴涵的信息进行相互补充和相互支撑. 我们要引导学生有序观察，多角度思考，保持信息的完整性，筛选出有效的信息，并提出问题，形成解决问题的方案.

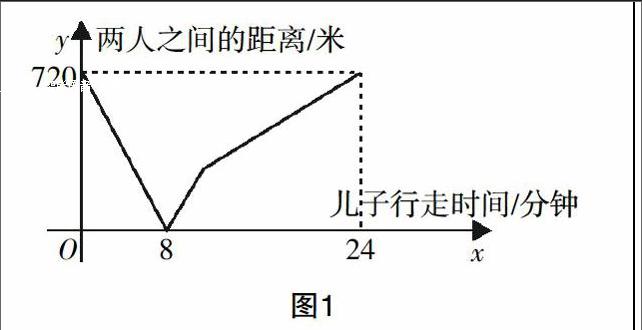
比如：爸爸从甲地走向乙地，儿子从乙地走向甲地，两人同时出发，两人之间的距离与儿子行走时间的关系如图1所示，根据图象可得爸爸比儿子每分钟多走（ ）米.

[儿子行走时间/分钟][两人之间的距离/米][720][O][x][y][8][24]

这是一道图文信息题，题干文字中提供了两个主要信息：一是爸爸和儿子是相向运动，二是求速度差. 图象中提供的信息更为丰富，图象的横坐标上，时间变量从0到24分钟，有8分钟和24分钟两个明确的时间信息；纵坐标上，路程变量是0到720米. 若图文相离，则信息不全，无从解题，甚至偏离正确的思路，使问题复杂化. 如果读图时，通过图文结合，整合信息，细心观察、分析图象含义，就可以抓住图中关键信息——8分钟和24分钟，算出父子速度以及儿子的速度，进而解决问题，即：①速度和：720÷8=90（米）②儿子速度：720÷24=30（米）③速度差：90-30=60（米）.

图绘结合，化静为动

静态的读图与动态的绘图操作，似乎是不相干的事，其实不然，“能根据文字绘出或想象出图意”是读图能力提高的一个标志. 读图需要借助对图形特征的认识、需要借助操作的经验和感知.陆游诗云“书上得来终觉浅，绝知此事需躬行.” 实践出真知，化静为动，图绘相益. 读图为绘图操作提供信息支持，画图操作为读图奠定感性基础. 图绘结合，有助于学生直观地读出信息，厘清数量关系.

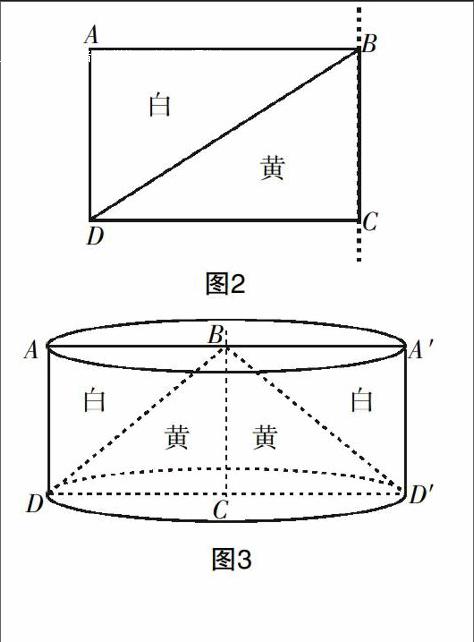
如图2：长方形ABCD以BC为轴旋转一周后，其中白色部分和黄色部分体积比是多少？面对这个静态的图形，学生会如何读图呢？经调查发现，学生读图解答时主要有三种情况：（1）从图中直观看图，轻率得出白色、黄色两部分经旋转后的体积比为1∶1；这种结论受到 “先入为主”效应的影响——学生直观感知：图形一样，旋转后的图形也一样，因而体积也一样. （2）根据题意进行想象，绕BC边旋转后是一个圆柱体；但学生想象会存在困难，分析结论时，意识停留在圆柱体沿直径的一个纵截面上——长方形AA′DD′（见图3），白色与黄色区域相同，得出体积相等的错觉；这种情况是学生想象能力发展水平还不够而引起的，也有学生探究问题的深度不够及对所学知识的概念理解不深入. （3）思维和空间想象能力比较强的孩子，凭借读图分析能顺利、正确解题；事实表明，这种情况为数不多，约占30%. 如果在读图时，教师引导学生采取“图绘结合、化静为动”策略，根据题意画出示意图（见图3），就很容易发现：黄色部分是一个与圆柱等底等高的圆锥，体积占圆柱体的三分之一，白色部分体积则占圆柱体的三分之二，从而得出V白和V黄的比是2∶1.

[D][A][B][C][白][黄][图2]

[D][A][B][C][白][黄][A′][D′][黄][白]

图形结合，化虚为实

小学生的思维发展，从感性思维向形象、抽象思维过渡，高年级学生已经具备了一定的空间想象能力，但发展水平还很有限；面对立体图形的读图，往往还是受年龄心理特征的约束，对想象的立体图形的感觉“虚而不实”，总体表现“平面强、立体弱”. 对于立体图形的读图能力的提高，我们认为可以图形结合，化虚为实. 利用实物或模型操作，既激发了学生的学习兴趣和学习积极性，同时带来真实、丰富的感知，积累大量的表象. 图形结合，还可以唤醒学生的生活体验和知识经验，建立起图象与立体图形的空间联系，形成“空间感觉”.

如图4，根据正面、上面、左侧面的视图，所观察到的物体是什么样子？共有多少块小正方体？本题的读图，需要较强的空间想象能力，要依据三份视图进行三维构建，学生无从下手或构建不完整. 教师可以引导学生用小正方体学具，尝试搭拼图型，再把图形与实物模型进行对照，打通平面图形与立体图形之间的联系，提高空间想象能力、读图能力. 当然，用尝试画图的方式，也能殊途同归，都能实现对学生读图能力的提升.

[正面][上面][左侧面][（Ⅰ） （Ⅱ） （Ⅲ） （Ⅳ）]

图策结合，化难为易

策，方法也. 分割、旋转、平移、转化、等量代换等方法都是读图活动中有效的策略. 高年级教学中，常有较为复杂的图形，往往数量关系较为隐蔽. 读图、分析处理图形信息时，借助这些策略，可以实现信息的有效转化，使读图化繁为简，化难为易，图形的数量关系进一步清晰，有利于形成简明的解题思路.

读图时，采用的策略不同，所获取的信息就不同，分析和解决问题的方法也就不同，应注重解题策略的优化. 如图5，求阴影部分的面积. 方法1：采用分割法，在正方形中添加对角线，把阴影部分分割成八个弓形，再求和. 方法2：重叠法；图中有4个半圆，即2个圆，试想，如果这2个圆铺满正方形，没有重叠，则2个圆的面积正好等于正方形的面积；而图形中有出现重叠，则说明2个圆的面积减去正方形的面积正好等于阴影部分的面积.

=[8 cm][8 cm]

又如图6：（1）面积比较：S△AOD（ ）S△BOC；（2）图中有（ ）对面积相等的三角形.学生在读图中，会凭视觉、直觉认为S△AOD略大，造成错误结论.如果在读图时，结合梯形的高或平行线之间距离相等的性质，就能读出图中△ACD与△BCD等底等高，即S△ACD=S△BCD，运用等量消去策略，减去S△ODC，可得S△AOD=S△BOC，进而得出图形中有3对面积相等的三角形. 读图中，能否运用相关的策略，读出图形信息，对于分析和解决问题至关重要.

[D][A][B][C][O]

总之，图形是一种数学语言，读图就是要读出图形所传递的数学信息；在小学高年级数学教学中，要激发学生读图兴趣，更要多渠道、多角度进行读图能力的培养，并进行必要的方法指导和训练，以期提升读图能力，乃至提高学生数学素养和数学能力.