高空高速拦截时导弹寄生效应影响分析*

李 亚

(中国空空导弹研究院制导控制系统研究所,河南洛阳 471009)

高空高速拦截时导弹寄生效应影响分析*

李 亚

(中国空空导弹研究院制导控制系统研究所,河南洛阳 471009)

高空高速拦截时,导弹制导时间常数和转弯速率时间常数较低空大幅增加,导引系统寄生耦合效应极有可能引起较大脱靶量,导致拦截失败。针对这一问题,文中建立五阶线性化制导控制系统模型,通过理论分析和仿真验证两种形式重点研究了寄生效应的影响因素及对制导性能的约束。结果表明,寄生效应制约着系统最小制导时间常数,提高系统响应快速性须首要缓解寄生效应;提升导弹攻击速度可有效减小寄生效应影响。

高空高速拦截;寄生效应;制导系统最小时间常数

0 引言

高空高速飞行器的快速发展迫使空空导弹的作战空域从低层稠密大气区拓展到30 km高度左右的稀薄流区。在高空,弹体过载响应性能很差,制导时间常数和转弯速率时间常数较低空大幅增加;此外,对高速目标实施拦截时,相对速度大、拦截时间短,很小寄生耦合效应都有可能引起大的脱靶量[1-2],导致拦截失败。因此,为解决高空高速目标的拦截问题,有必要对现役空空导弹上广泛采用的比例导引律在高空高速环境下的寄生效应影响进行分析,从而为该作战环境下的制导控制系统设计提供参考。

文中首先建立五阶线性化制导控制系统模型,通过理论分析和仿真验证来重点研究高空高速拦截时寄生效应的影响因素及其对制导性能的影响。

1 制导控制系统模型

结合高空高速拦截的技术特点,为便于模型的推导,作如下假设:

a)末制导时间短,可假定弹目接近速度Vc近似为常量[3];

b)暂不考虑加速度指令限幅。

1.1 寄生回路模型

以某雷达导引系统[4]为例,如图1所示。R为天线罩斜率,θH为导引框架角,r=R·θH为天线罩折射角,ε为跟踪误差角,D为光轴倾角,γ为速度倾角,α为攻角。

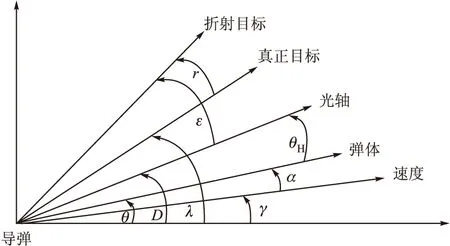
图1 某雷达导引头天线罩几何关系

由图1知,θ=α+γ那么:

(1)

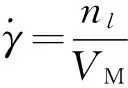
(2)

同时:

(3)

至此,可建立寄生效应模型如图2所示。

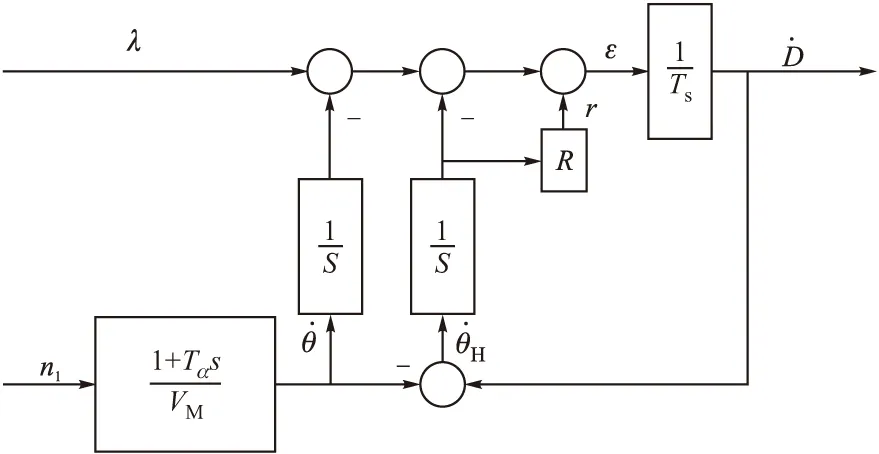
图2 导引系统寄生回路

红外成像导引头的寄生效应[5-7]源于伺服平台的摩擦力矩,原理与此基本类似。

1.2 噪声滤波器模型

1.3 飞控系统模型

1.4 制导控制系统模型

图3 五阶线性化制导控制系统

2 寄生效应对比例制导性能的影响

采用理论分析和数字仿真验证的形式对高空高速拦截时寄生效应的影响进行研究。首先根据图3推导出了寄生效应影响模型,理论分析给出定量结论,再通过数字仿真进行验证。

2.1 理论分析

(4)

(5)

(6)

(7)

(8)

继续推导得:

(9)

因tgo=tF-t(tF为制导时间,t为当前时刻)则:

(10)

代入式(9)得:

(11)

通常情况下|R|≪1,则Fτ-R≈Fτ,那么:

(12)

2.2 仿真验证

数字仿真验证时,取T=0.5,nT=1g,Tα=5,R=-0.01。结果如图4、图5所示。

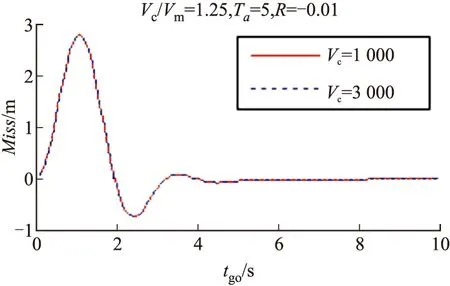
图4 相同Vc/Vm下寄生效应的影响

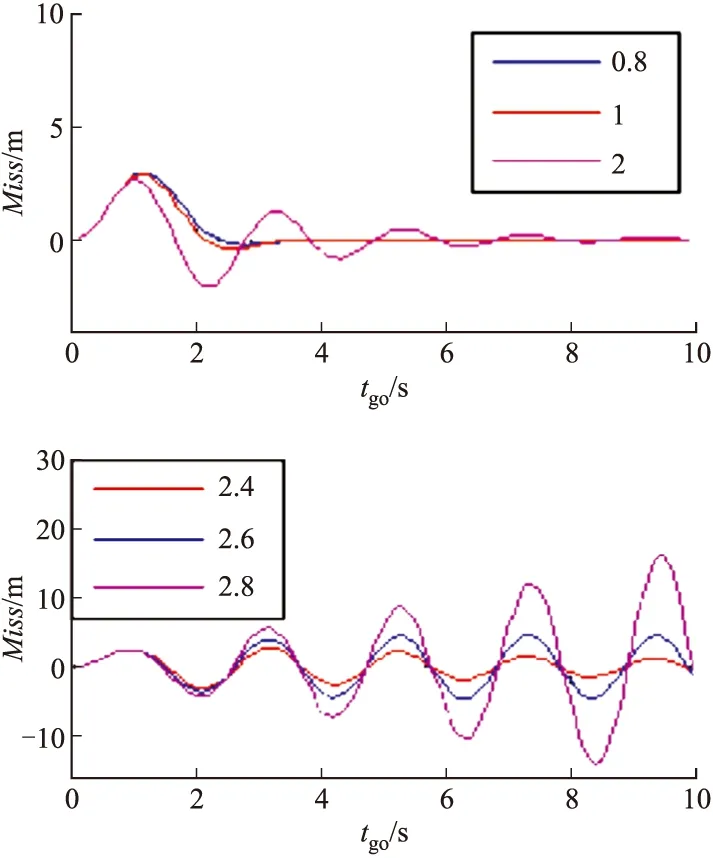
图5 不同Vc/Vm下寄生效应的影响

对于特定的控制系统,适当增大制导时间常数可在一定程度上缓解寄生效应的影响(如表1所示,R=-0.01)。

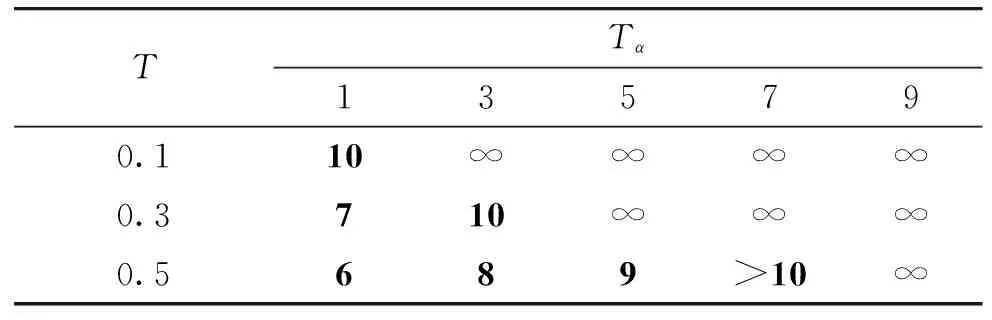
表1 稳定控制系统Tα和T匹配性统计

分析表1可知,当天线罩斜率R一定时,随着转弯角速率时间常数Tα的增大,控制系统最小制导时间常数T也在逐步增大;且Tα与系统稳定性成反比。

对控制系统进行稳定性分析。

(13)

通常有Tα/T>1,则由稳定性判据可得制导系统最小时间常数为:

(14)

可知,制导系统最小时间常数与转弯角速率时间常数Tα、导引头天线罩斜率R成正比。设计小的制导时间常数必须首先设法减小Tα和R,即减小寄生效应。

在高空,Tα通常较大,即便使用姿控直接力系统对Tα的改善效果也并不明显。而对于R,可通过设计自适应算法进行实时补偿。由表1可知,Tα=5,R=-0.01时,制导时间常数T须大于0.4,否则系统就会失稳;但若通过自适应补偿将R降到-0.001,那么制导系统时间常数就可减至0.1,从而大大提高系统响应的快速性。这一点对机动目标的高空高速拦截至关重要。

反过来,对于特定的制导控制系统,假定期望的制导时间常数为T,由式(14)可知,其所能容忍的最大天线罩斜率为:

(15)

如果R>Rmax,须通过某种方式将其有效值补偿到Rmax以下,以保证制导时间常数能够降至期望水平。否则即使采用直接力控制将制导时间常数降至某一极小值,也无法工程应用。

3 结论

高空高速拦截时,弹体转弯角速率时间常数较低空时大幅增加,加剧了系统的寄生耦合效应,严重约束着其响应快速性的提升。文中基于五阶线性化制导控制系统模型,理论、仿真研究了高空高速拦截时寄生效应对比例制导律性能的影响,形成结论如下:

2)寄生效应制约着系统最小制导时间常数,提高系统响应快速性须首要缓解寄生效应。

[1] 李富贵, 夏群利, 祁载康. 导引头隔离度寄生回路对最优制导律性能的影响 [J]. 宇航学报, 2013, 34(12): 2658-2667.

[2] Nesline F W, Zarchan P. Radome induced miss distance in aerodynamically controlled homing missiles [C]∥Proceedings of AIAA Guidance and Control Conference, AIAA, New York, 1984.

[3] Zarchan Paul. Tactical and Strategic Missile Guidance [M]. 5thEdition. Progress in Astronautics and Aeronautics,Volume 219. Published by the American Institute of Aeronautics and Astronautics Inc, 2007.

[4] 王嘉鑫, 林德福, 祁载康, 等. 全捷联相控阵雷达导引头隔离度寄生回路研究 [J]. 北京理工大学学报, 2013, 33(11): 1124-1129.

[5] 周卫文, 梁晓庚, 贾晓洪. 平台式导引头跟踪回路对制导系统的影响 [J]. 四川兵工学, 2011, 32(5): 1-4.

[6] 崔莹莹, 夏群力, 祁载康. 导引头稳定平台隔离度模型研究 [J]. 弹箭与制导学报, 2006, 26(1): 22-25.

[7] 杜运理, 夏群利, 祁载康. 导引头隔离度相位滞后对寄生回路稳定性影响研究 [J]. 兵工学报, 2011, 32(1): 28-32.

[8] Nesline F W, Zarchan P. A new look at classical versus modern homing guidance [J]. Journal of Guidance and Control, 1981, 4(1): 78-85.

Investigation on Parasitic Effects for Intercepting High-speed and High-altitude Targets

LI Ya

(Guidance and Control System Department，China Airborne Missile Academy, Henan Luoyang 471009, China)

Since there would be a significant increase in missile guidance time constant and turning rate time constant when intercepting high-altitude and high-speed targets, compared with those at low altitude, small parasitic effect of seeker could probably cause large miss, resulting in failure of intercepting mission. To deal with this issue, the fifth-order linearized mathematic model was constructed on guidance and control system and both analytical ways and simulation ways were employed to investigate parasitic effect’s relating factors and its influence on performance of proportional guidance. The results show that the parasitic effects of seeker constrain the guidance time constant, it means that a smaller guidance time constant must firstly loose the system parasitic effects and this could be reached by improving the missile’s speed.

high-speed and high-altitude target interception; parasitic effect; minimum time constant of guidance system

2014-08-17

航空基金(20120112001)资助

李亚(1983-),男,河南商丘人,工程师,硕士研究生,研究方向:空空导弹精确制导技术。

V448.234

A