具有碰撞角约束的微分对策导引律研究*

徐兴元,蔡远利

(1 河南科技大学信息工程学院,河南洛阳 471023;2 中国空空导弹研究院,河南洛阳 471009;3 西安交通大学电子与信息工程学院,西安 710049)

具有碰撞角约束的微分对策导引律研究*

徐兴元1,2,蔡远利3

(1 河南科技大学信息工程学院,河南洛阳 471023;2 中国空空导弹研究院,河南洛阳 471009;3 西安交通大学电子与信息工程学院,西安 710049)

控制碰撞角度可以提高拦截弹的打击效果。文中提出了一种具有碰撞角约束的微分对策导引律,能够同时对脱靶量和碰撞角进行控制。把拦截弹和目标当作两个独立的受控对象,通过最小化代价函数同时得到了拦截弹的最优机动策略和目标的最优逃避策略。仿真结果表明,文中提出的微分对策导引律适用于拦截高速机动目标,而且在满足厘米级脱靶量的情况下,拦截弹在交汇点处不需要过大的横向加速度指令,从而避免指令被限幅。

拦截弹;碰撞角;微分对策导引律;机动目标

0 引言

传统的比例导引律不能实现对终端碰撞角度的控制,但是一些比例导引律的变种形式,可以实现预先确定的碰撞角度[1-4]。偏差比例导引律[1]是在传统的比例导引律的基础上再加上一项随时间变化的偏差项,这一偏差项可以使导弹以特定的角度碰撞目标。椭圆弧导引律[2]是另一种针对静止目标的偏差比例导引律,这种制导方法假定导弹始终位于一条预先确定的连接导弹和目标的椭圆弧上,且所需的终端速度方向位于目标点的切线上,因此只要控制导弹沿该椭圆飞行,即可在命中目标的同时满足碰撞角度要求。变系数比例导引律[3]是根据弹目运动的数学模型,通过在线调整导引系数以满足终端角度约束的一类导引律。基于虚拟目标的轨迹预测比例导引律[4]首先设计以期望角度向真实目标运动的虚拟目标,然后控制导弹追踪此虚拟目标并保证终端时刻形成尾追状态,从而满足末速方向要求。上述几种比例导引律的变种形式都具有制导形式简单,对导航信息偏差的敏感性较低的优点,但所得到的导引律依赖于各种假设与简化,仅适用于静止目标或者缓慢移动的目标。

以最优控制理论为基础的最优导引律可以考虑导弹和目标的动力学问题,并可以考虑制导过程起点或终点的约束条件或其它约束条件,如能量消耗最少、终端脱靶量最小、最短时间、最小控制量、特定的碰撞角度等。Ryoo等[5]研究了匀速导弹具有碰撞角度和控制量约束的最优导引律。Sang等[6]提出了基于李雅普诺夫稳定理论和参数最优化方法的碰撞角控制导引律。Lee等[7]提出了同时控制时间和碰撞角度的最优导引律。Lee等[8]设计了同时满足终端角度和加速度约束的最优导引律。最优导引律的缺点体现在,对目标加速度估计误差、剩余飞行时间估计误差灵敏度高,对测量元件也提出很高的要求。另外,最优导引鲁棒性较差。

微分对策的概念早在20世纪50年代就提出来了,但一直未在导弹制导领域得到重视。微分对策导引律是将最优控制与对策论相结合得到的。微分对策导引律与最优导引律的区别在于:最优导引律是一个单边优化问题,所得到的仅仅是拦截弹的最优机动策略;而微分对策导引律是一个双边优化问题,通过最小化代价函数同时得到拦截弹的最优机动策略和目标的最优逃避策略。由于在实战中导弹和目标是一对独立受控对象。显然,基于“零和博弈”思想的微分对策导引律更符合工程需要。

总体来讲,现有的各种具有角度约束的导引律,针对静止目标或者缓慢移动的目标具有较好的性能,而对于高速机动目标,这些导引律往往并不具备足够高的精度。原因在于过小的脱靶量往往需要拦截弹在交汇点处提供很大的横向加速度,甚至造成制导指令被限幅,引起脱靶。文中提出的具有碰撞角约束的微分对策导引律可以克服这一问题。

1 问题描述与建模

末制导段的弹目运动关系如图1所示。假定拦截弹和目标的运动为二维平面飞行,二者的速度均为常量。由于末段飞行时间较短,假定拦截弹和目标速度与初始视线的夹角为小量,运动方程可以沿初始视线线性化。

图1 拦截弹和目标平面飞行简图

图1中,X轴沿初始视线方向;下标P(Pursuer)表示拦截弹的相关状态,下标E(Evader)表示目标的相关状态;VP和VE分别为拦截弹和目标的速度;aP和aE分别为拦截弹和目标的横向加速度;γP和γE分别为拦截弹和目标的弹道倾角;弹目相对距离为R;θ为视线角;弹目双方偏离初始视线的相对位移表示为y。aP和aE垂直于X轴的分量表示为aPN和aEN,且aPN=aPcosγP0,aEN=aEcosγE0。根据各个物理量的定义,弹目相对运动方程[9]为:

(1)

(2)

(3)

(4)

假定目标的横向加速度是一阶滞后的,则:

(5)

为了较好的表达文中的研究思想,把拦截弹当作零阶滞后系统处理,即:

(6)

如果考虑系统滞后,可以按照类似的方法处理,但导出的导引律形式要复杂得多。

根据上文的描述,给出如下线性系统模型:

(7)

式中:状态变量x1=y;x2为弹目相对横向加速度;x3为目标的横向加速度;x4为期望碰撞角度,x4=γP+γE。

系统状态方程为

(8)

式中:uP为拦截弹的制导指令;uE为目标弹的制导指令。根据式(7)～式(8)有:

(9)

(10)

假定在中制导律的作用下,γP+γE大致满足期望的碰撞角,而且弹目双方在飞行末段偏离飞行三角形小量。因此,三角形得以维持,弹目接近速度近似为常量,剩余飞行时间用下式估计[9]:

(11)

2 导引律推导

考虑到终端状态误差最小和最少的能量消耗,定义线性二次型性能指标为[10]:

(12)

式中:e(tf)=x(tf)-xf为终端状态误差,xf为期望状态。(e(tf))TSe(tf)体现了对终端状态误差的约束。最小化代价函数(12)分别得到满足终端状态误差的拦截弹最小控制量uP(t)和目标弹最大控制量uE(t)。μ为弹目双方机动能力的比值。文中的导引律要求对脱靶量和碰撞角度进行控制,也就是控制状态x1和x4,通过下式对系统简化。

(13)

式中:Ω(tf,t)为状态转移矩阵;D为一常矩阵,且:

(14)

Ω(tf,t)=

(15)

新变量Z(t)的导数为:

(16)

选取加权矩阵:

(17)

式中a1和a2为非负常数。定义γf=γP+γE,tg=tf-t,代价函数式(12)变为:

(18)

当考虑目标横向加速度滞后时,所得到的导引律形式比较复杂,下面仅给出目标横向加速度零滞后,即τE=0时的导引律。令τE=0,则:

(19)

(20)

利用最优控制理论的方法,根据式(18)～式(20),求解出拦截弹和目标的最优制导律分别为:

(21)

式中:

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

引入变量Z(t),不仅使问题得到了简化,而且Z(t)有重要的物理意义。Z1(t)表示零控脱靶量,Z2(t)表示零控碰撞角。Z1(t)和Z2(t)如下式所示:

(31)

(32)

为了应用式(21)所示的微分对策制导律,拦截弹需要获取必要的信息。假定拦截弹能够获取视线角θ(t)的信息且θ(t)为小量,则y≈θR,有:

(33)

3 性能分析

利用表1所示的参数验证所提出导引律的有效性。所得的仿真结果如图2～图6所示。图2表示具有各种碰撞角的弹目飞行轨迹;图3表示对应图2中各条飞行轨迹的拦截弹最优制导指令;图4表示对应图2中各条飞行轨迹的目标弹最优制导指令;图5表示脱靶量的变化;图6表示碰撞角的变化。仿真结果表明,在满足0.1 m脱靶量的条件下,能够同时控制碰撞角度,且所需的制导指令不大,可以避免指令被限幅。另外,在仿真时假定拦截弹和目标的速度均为1 500 m/s,也就是说,拦截弹相对于目标并没有速度优势,这是所提出导引律的一大优势。由图3看出,当碰撞角太大时,拦截弹的最大制导指令明显变大,因此,对于特定的碰撞角,选择合适的初始角度可以有效减小最大制导指令。

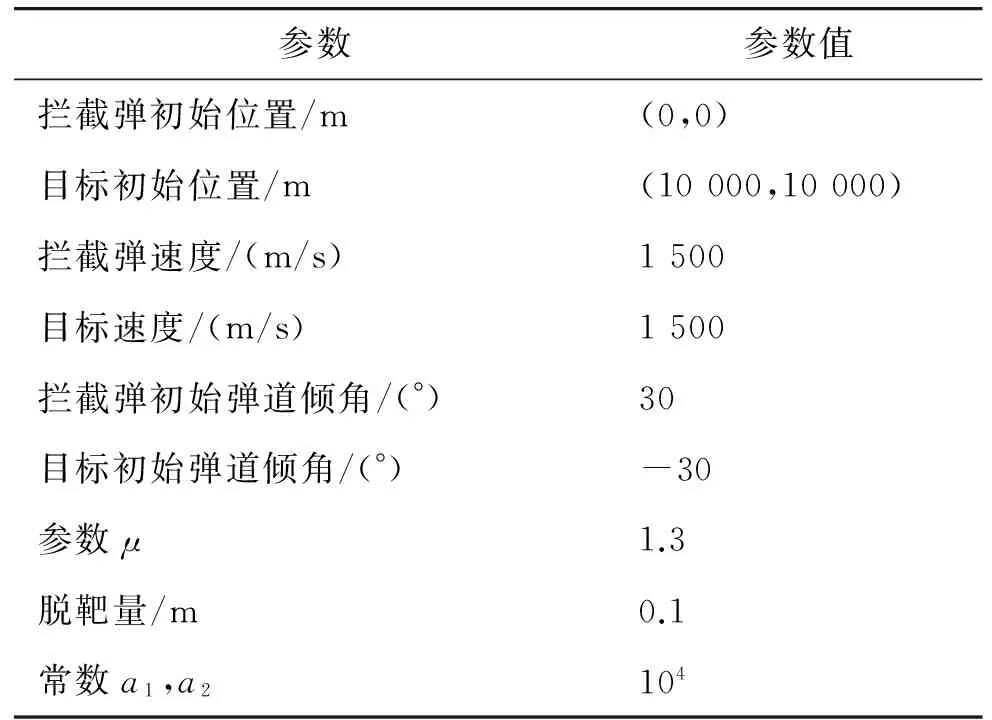
表1 非线性仿真的初始参数

图2 弹目飞行轨迹

图3 拦截弹制导指令

图4 目标弹制导指令

图5 脱靶量的变化

图6 碰撞角的变化

4 结束语

文中提出了一种具有碰撞角约束的微分对策导引律,文中给出了较详细的推导过程并通过数字仿真验证了其有效性。当设定脱靶量为0.1 m,拦截弹和目标具有相同的初始速度时,拦截弹在交汇点处不需要太大的横向加速度指令。虽然微分对策导引律是在假定弹目双方偏离初始视线小量的情况下,通过运动方程线性化得到的,但仿真结果表明弹目双方偏离初始视线较大时,导引律仍然具有很好的性能。

文中提出的微分对策导引律依赖精确估计剩余飞行时间,因此研究更精确的估计剩余飞行时间的方法是必要的。另外,拦截弹初始发射角度对制导性能有很重要的影响,对于特定的碰撞角,选择合适的初始角度可以减小最大制导指令,这也是今后的一个研究内容。

[1] Kim K S, Jung B, Kim Y. Practical guidance law controlling impact angle [J]. Journal of Aerospace Engineering, 2007, 221(1): 29-36.

[2] Yoon M G. Relative circular navigation guidance for three-dimensional impact angle control problem [J]. Journal of Aerospace Engineering, 2010, 23(4): 300-308.

[3] 朱战霞, 王建培. 一种攻击地面固定目标的变系数比例导引律 [J]. 飞行力学, 2000, 18(4): 46-49.

[4] 张汝川, 顾文锦, 赵红超. 基于落角约束的超声速导弹制导方案研究 [J]. 飞行力学, 2009, 27(3): 45-49.

[5] Ryoo C K, Shin H S, Tahk MJ. Energy optimal waypoint guidance synthesis for antiship missiles [J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 80-95.

[6] Sang D, Min B M, Tahk M J. Impact angle control guidance law using Lyapunov function and PSO method [C]∥ SICE Annual Conference, Kagawa University, Japan, 2007.

[7] Lee J I, Jeon I S, Tahk M J. Guidance law to control impact time and angle [J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 301-310.

[8] Lee Y, Ryoo C, Kim E. Optimal guidance with constraints on impact angle and terminal acceleration [C]∥AIAA Guidance, Navigation and Control Conference, Austin, USA, 2003.

[9] George M Siouris. Missile guidance and control systems [M]. New York, USA, Springer, 2004: 181-207.

[10] 吴受章. 最优控制理论与应用 [M]. 北京: 机械工业出版社, 2008: 59-75.

Differential Game Guidance Law with Impact Angle Constraint

XU Xingyuan1,2,CAI Yuanli3

(1 Information Engineering College，Henan University of Science and Technology, Henan Luoyang 471023, China;2 China Airborne Missile Academy, Henan Luoyang 471023, China;3 School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710079, China)

Control of impact angle can considerably increase interceptor’s lethality in terminal engagement. A differential game guidance law was proposed in this paper, which can achieve a specified impact angle as well as zero terminal miss distance. The adversaries in conflict were considered as two independent controlled objects, through minimizing the cost function, one can obtain the adversary’s optimal maneuver strategy simultaneously. Simulation results show that the proposed guidance law is suitable for intercepting high-speed maneuvering target., and, centimeter level miss distance requires less guidance command to avoid command saturation near terminal time.

antimissile interceptor; impact angle; differential game guidance law; target maneuver

2014-07-29

中国博士后科学基金(2013M542002);航空科学基金(20130142002)资助

徐兴元(1972-),男,河南洛阳人,博士,研究方向:导航、制导与控制。

V249.12

A