火箭发动机平衡流与非平衡流模拟研究*
刘 仔,李艳臣
(1 哈尔滨工程大学航天与建筑工程学院,哈尔滨 150001;2 上海卫星装备研究所,上海 200240)
火箭发动机平衡流与非平衡流模拟研究*
刘 仔1,李艳臣2
(1 哈尔滨工程大学航天与建筑工程学院,哈尔滨 150001;2 上海卫星装备研究所,上海 200240)
文中通过数值模拟研究平衡流与非平衡流的差异和适用情况,为两相流数值模拟中选择合理的计算模型提供相应的参考。采用高雷诺数条件下的k-ε湍流模型、双流体模型以及全流速SIMPLE方法分别对发动机内的两相平衡流与非平衡流进行模拟研究。计算结果表明,平衡流与非平衡流计算得到的两相流场在喷管的扩张段存在差异,且差异随着膨胀比的增加而更加明显,因此当喷管扩张比较大时按非平衡流计算更准确。
k-ε湍流模型;双流体模型;平衡流;非平衡流
0 引言
现代固体火箭发动机广泛采用含有金属颗粒的复合推进剂,而复合推进剂燃烧形成的两相流动对固体火箭发动机的性能存在巨大的影响。目前,两相流场对发动机性能、颗粒沉积和流场的影响国内外都进行了大量研究工作[1-6],但固体火箭发动机内的两相流场仍然存在着许多的问题亟待解决,比如对于两相平衡流与非平衡流的模拟研究就相对较少。平衡流与非平衡流是根据流体相与颗粒相之间的滞后进行区分的,两相无滞后为平衡流,两相滞后为非平衡流。将固体火箭发动机的内流场看作平衡流或者非平衡流分别进行数值计算时得到的发动机性能与内流场的结构存在巨大的差异,因此研究平衡流与非平衡流计算结果的差异和适用条件具有重要的工程实际意义。
1 数值计算方法
在推导气相与颗粒相的控制方程时,需要给出忽略颗粒布朗运动所贡献的压强、颗粒内部温度一致和颗粒满足拟流体假设等假设[7]。利用雷诺输运定理推导得出双流体模型中颗粒相与气相的控制方程。
1.1 气相控制方程湍流模型选择
连续方程:
(1)
动量方程:
(2)
能量方程:
(3)
在进行数值计算时,文中选择RNGk-ε两方程湍流模型,采用标准壁面函数法对发动机壁面进行处理。
1.2 颗粒相控制方程
连续方程:
(4)
动量方程:
(5)
能量方程:
(6)
1.3 物理模型与边界条件
计算模型如图1所示。固体火箭发动机两相流中颗粒相为Al2O3,气相则为推进剂燃烧产生的燃气。Al2O3颗粒的直径为3.0 μm,质量分数为16.7%,密度为3 960.0 kg/m3,比热为1 408.0 J/(kg·K),燃气的定压比热为1 667.43 J/(kg·K)。选择入口a为质量流量入口,两相总的质量流量为3.0 kg/s,气相与颗粒相的总温设置为3 200.0 K,壁面b设置为固定无滑移壁面,对称轴c设置为对称轴边界,出口d设置为压力出口。

图1 物理模型
2 算例验证
利用文中的计算方法对文献[8]中的算例进行模拟。由图2可知,文中计算结果与文献结果基本一致,验证了文中计算方法的合理性与正确性。
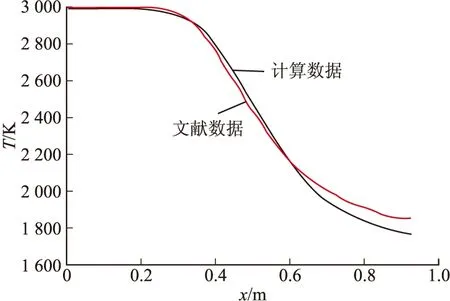
图2 喷管轴线混合物温度对比
3 计算结果分析
由图3可知,在喷管内平衡流与非平衡流计算得到的颗粒体积分数分布存在巨大差异。非平衡流计算结果表明,在喷管扩张段内存在明显的无颗粒区;在喷管收敛段内,流场受固壁的限制,在壁面附近形成颗粒聚集现象,在惯性力作用下,形成了喷管喉部下游的粒子聚集带,该现象与文献[9]一致。平衡流的计算结果表明,在喷管扩张段内不存在无颗粒区。平衡流与非平衡流结果的不同是因为平衡流忽略颗粒与气相之间的滞后,即在非平衡流中颗粒的随流性比平衡流差。非平衡流中喷管内的无颗粒区在扩张段内是先增大后减小,因为该发动机的喷管扩张段是曲线型面,出口位置壁面的曲率小于中部位置壁面的曲率,而颗粒的随流性较差,无法完全按照喷管型面变化进行运动。

图3 喷管内颗粒的体积分数
由图4可知,在发动机喷管扩张段轴线上平衡流的混合物速度较非平衡流的混合物速度高,且差值随着喷管膨胀比的增大而增大;因为非平衡流中考虑气相与颗粒滞后的影响,而平衡流不考虑气相与颗粒滞后的影响,即两相流损失平衡流小于非平衡流,同时该影响随着混合物的膨胀而不断的积累。由图5可得,在发动机轴线扩张段上平衡流中颗粒的速度高于非平衡流中颗粒的速度,其中颗粒速度的差值随着喷管膨胀比的增大而增大;因为平衡流中不考虑两相之间的滞后,即平衡流中颗粒的速度与气相的速度始终保持一致,而非平衡流中颗粒的速度低于气相的速度。
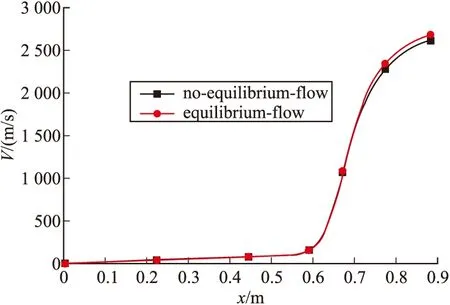
图4 发动机轴线混合物速度

图5 发动机轴线颗粒速度
由图6可得,平衡流与非平衡流计算得到的轴线混合物温度存在差异,其中差异随着喷管膨胀比的增大而加剧;因为平衡流中不考虑两相滞后损失,即平衡流中混合物的膨胀能力高于非平衡流中混合物的膨胀能力,两相损失逐渐积累增大,所以平衡流的混合物温度低于非平衡流的温度,差值逐渐增大。由图7可知,平衡流与非平衡流计算得到的轴线气相马赫数在喷管扩张段明显不一致;因为平衡流中不考虑两相滞后的影响,即平衡流中颗粒的运动不需气相的带动,对气相的膨胀抑制作用小于非平衡流,所以平衡流的气相马赫数高于非平衡流,同时由于影响作用的不断积累,导致气相马赫数的差值随着喷管膨胀比的增大而增大。
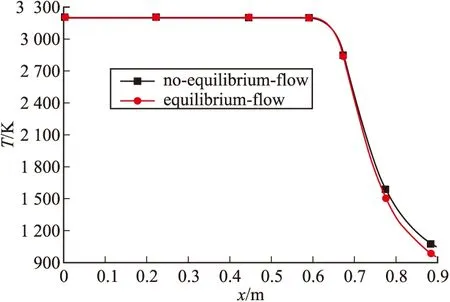
图6 发动机轴线混合物温度

图7 发动机轴线气相马赫数
推力F是固体火箭发动机的主要性能参数之一,推力系数Cf是表征喷管性能的参数[10],其中Cf=F/(PcAt)。表1给出了平衡流与非平衡流条件下发动机的推力与推力系数。由表1可知,按非平衡流计算得到的发动机推力小于按平衡流计算得到的发动机推力,推力系数非平衡流大于平衡流;因为平衡流不考虑两相滞后损失,非平衡流要考虑两相滞后损失。

表1 两种流动下发动机的性能参数比较
4 结论
通过对固体火箭发动机内的平衡流与非平衡流进行模拟研究,发现非平衡流与平衡流模拟结果存在很大差异。其中在发动机喷管扩张段轴线上两种流动计算得到的物理参量差异比较明显,同时差值随着喷管膨胀比的增大而增大;在发动机喷管扩张段内非平衡流存在着明显的无颗粒区,而平衡流基本不存在无颗粒区;两种流动计算得到的发动机推力、推力系数也存在差异。综上当喷管扩张比不大时两种模型均适用,并且都能得到比较一致的结果,但当喷管扩张比较大时选择非平衡流进行计算相对较好,可以避免按平衡流计算带来的误差。
[1] Hwang C J, Chang G C. Numerical study of gas-particle flow in a solid rocket nozzle [J]. AIAA Journal, 1988, 26(6): 682-689.
[2] Sachdev J S, Groth C P T, Gottlieb J J. Numerical solution scheme forinert, disperse, dilute gas-particle flows [J]. International Journal of Multiphase Flow, 2007, 33(3): 282-299.
[3] 武利敏. 固体火箭发动机两相流计算模型分析与比较 [D]. 哈尔滨: 哈尔滨工程大学, 2007.
[4] 于勇, 张夏, 陈维. 用双流体模型模拟超音速气固两相流动 [J]. 航空动力学报, 2010, 25(4): 800-807.
[5] 吴限德, 张斌, 陈卫东, 等. 固体火箭发动机喷管内气粒两相流动的CFD-DSMC模拟 [J]. 固体火箭技术, 2011, 34(6): 707-710.
[6] 贺征, 郜冶, 顾璇. 锥柱型装药固体火箭发动机两相内流场中颗粒运动的数值模拟 [J]. 宇航学报, 2005, 26(3): 354-357.
[7] 方丁酉. 两相流体力学 [M]. 长沙: 国防科技大学出版社, 1988: 1-68.
[8] 刘晓俐. 高金属含量固体火箭发动机的相关问题研究 [D]. 哈尔滨: 哈尔滨工程大学, 2006.
[9] 李东霞, 徐旭, 蔡国飙, 等. 火箭发动机气体-颗粒两相流双流体模型研究 [J]. 固体火箭技术, 2005, 28(4): 238-243.
[10] 董师颜, 张兆良. 固体火箭发动机原理 [M]. 北京: 北京理工大学出版社, 1996: 31-33, 95, 101-126.
Simulation Research of Equilibrium Flow and Non-equilibrium Flow in Rocket Motors
LIU Zai1,LI Yanchen2
(1 College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China;2 Shanghai Institute of Spacecraft Equipment, Shanghai 200240, China)
To provide corresponding reference for choosing reasonable calculation model in numerical simulation of two-phase flow, the difference and suitable situation of equilibrium flow and non-equilibrium flow were studied through numerical simulation. Thek-εturbulence model under high Reynolds number, two-fluid model and full-speed SIMPLE method were used to simulate equilibrium flow and non-equilibrium flow in solid rocket motors. Calculation results show that the difference existing in the expansion nozzle segment, and the difference is more obvious with increase of expansion ratio. We can conclude that the simulation result of two-phase is more accurate when the expansion ratio of nozzle is relatively large.
k-εturbulence model; two-fluid model; equilibrium flow; non-equilibrium fow
2014-07-11
刘仔(1991-),男,四川邻水人,学士,研究方向:固体火箭发动机内的流动、传热与燃烧。
V435
A

