基于线性方程组的门限匿名认证方案

殷凤梅，濮光宁，张 江，侯整风

1.合肥师范学院，合肥 230601

2.安徽财贸职业学院，合肥 230601

3.合肥工业大学 计算机与信息学院，合肥 230009

1 引言

随着计算机网络的飞速发展，电子商务、电子政务和网上银行得到广泛应用，此类应用中，为了增强系统的安全性能，身份认证技术必不可少，在一些特殊的场合下，认证的身份还需要匿名保护。因此，匿名认证[1]成为了信息安全领域的研究热点，很多无条件匿名认证方案[2-7]应运而生。可对于完备的匿名认证，可追踪的匿名认证可以防止“匿名”特性被滥用。

2001年，Shouichi和Susumu[8]基于随机自规约关系产生了临时的公私钥，实现了移动环境下的可追踪匿名认证方案，但该方案中存在可信中心权利过大的问题。2005年，田子健等[9]借鉴环签名的思想，提出一种动态可追踪的匿名认证方案，该方案既可以由示证人自由选择匿名子集，又可以追踪匿名的身份。2008年，Jung等人[10]提出了A3RP协议，实现可追踪的匿名认证方案。但这两个方案的匿名追踪不是门限追踪，容易导致成员的身份信息被随意的追踪，降低了隐私的安全性。2012年，刘方斌等[11]借助民主签名思想提出了无可信中心的门限追踪Ad Hoc网络匿名认证，有效地解决了Ad Hoc网络中的匿名认证问题，但该方案采用Shamir的Lagrange插值算法计算成员的秘密份额和群公钥，计算和相互通信开销较大，效率较低。

本文借助石润华等人[12]提出的门限秘密共享的思想，提出了一种基于线性方程组的门限匿名认证方案，其安全性依赖于离散对数求解的困难性。与文献[11]相比，秘密份额和群公钥的计算代价较小，匿名认证过程更简单。

2 基于线性方程组的门限匿名认证方案

2.1 系统初始化

本文方案是基于线性方程组的求解理论，当系数矩阵的秩等于t时，可以求出t个未知变量，继而得到每个成员的秘密份额。

方案中存在n个成员Ui(1≤i≤n)，可信中心选取参数p、g并公开。其中，p是安全的大素数，q是p-1的素因子，g是GF(p)上的q阶生成元。

定义一个序列如下：

其中，c0是n个成员共享的秘密，c1，c2，…，ct-1是t-1个随机数（要求ci(0≤i≤t-1)之间线性无关），每个si(0≤i≤n)由它前面的t项相加modp得来。即

因此，产生如下线性方程组：

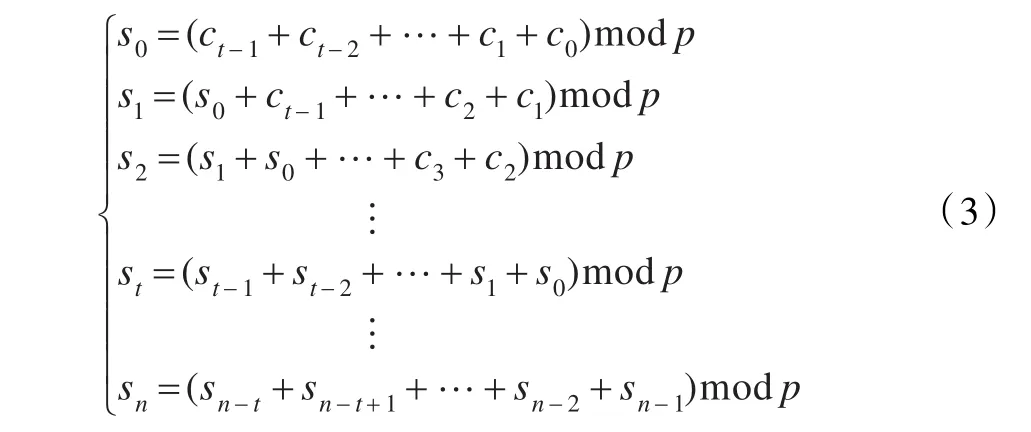
由于s0与共享的秘密c0直接相关，因此对s0保密。将式（3）中每个方程均用ci(0≤i≤t-1)表示，可以得到式（4）：

其中，Bn×t成员可以计算得到，即相当于对所有成员公开。将si作为秘密份额分发给用户Ui，公开C0，计算成员Ui的公钥Si并公开。C0、Si可通过式（7）、（8）计算得到：

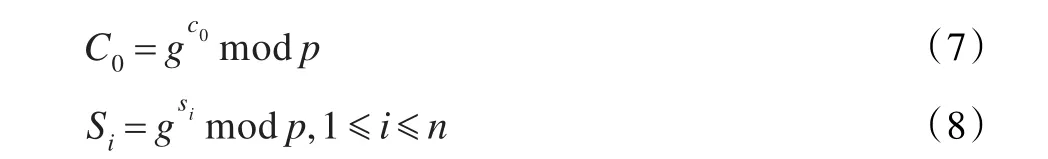
由于C是t维向量，反过来，共享的秘密c0与t个成员si之间的关系可以用式（9）表示：

而bji′(1≤i≤t)可以由矩阵 B计算得到。

2.2 匿名认证

匿名认证包含两个方面：一要求示证者可以证明自己的身份；二要求在认证中不泄露示证者的身份信息。

示证者Up想证明自己属于组织U，为了不暴露自己的身份，需要其余任意t-1个成员协助，组成认证集合UR={U1，…，Ut-1，Up}。

随机数的详细获取过程可参考文献[13]。

（4）Up根据式（10）计算Kp并公开，根据式（11）计算Ep并公开：

（5）Up秘密地选随机数hp，根据式（12）计算Hp并公开，根据式（13）计算Qp并公开：

（6）认证集合UR中每个成员Ui(i∈UR)，根据式（14）计算fi：

（7）根据式（15）联合计算Fp：

（8）若式（16）成立，则证明Up属于组织U：

2.3 匿名追踪

为了防止“匿名”特性被滥用，在某些情况下，需要追踪并揭示示证者的身份信息，即考虑匿名可控问题。如此一来，匿名认证和匿名追踪似乎有些矛盾，为了兼顾两者，匿名追踪不能是随意的追踪，必须是达到门限值t个成员，联合才能追踪示证者的身份，即实现匿名的门限追踪。

（1）t个成员记为Ui(1≤i≤t)组成追踪集合UZ={U1，U2，…，Ut}，使用各自的秘密份额根据式（17）计算wi，并根据式（18）联合计算Wp：

（2）根据式（19）可得到示证者的公钥，即示证者的身份：

2.4 实验数据

令n=11，t=5，p=47，根据式（4），si可由ci(0≤i≤4)线性表示，两者之间的线性关系可以使用矩阵表示，如式（20）：

假设共享的秘密c0=13，根据文献[14]的证明，取生成元g=5，根据式（7）计算C0=513mod47=43并公开。选取随机数c1=3，c2=7，c3=9，c4=11。

（1）根据式（20）计算可得si序列：

（2）如果U6想证明自己属于组织U，需要组织中的4个成员，假设是U1，U3，U4，U8协助认证，则认证集合UR={U1，U3，U4，U8，U6} 。

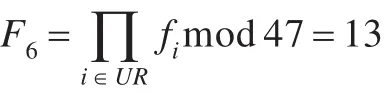
以上随机数ci以及p等数据的选择都是一般的整数，主要用来模拟验证方案的正确性，在实际应用中，可以从Miracle大数运算库选择位数较高的大数，提高方案的安全性。

3 方案分析

3.1 正确性

（1）系统初始化的正确性分析

n个成员可通过式（4）获得各自的秘密份额，且成员数n可以任意扩展。

由于每个si(0≤i≤n)由它前面的t项相加modp而得，因此所有的si都可以转换成由ci(0≤i≤t-1)线性表示，即通过式（4）所示的方程组求解。另外，每个si都由它前t项计算得来，因此，式（2）所示的序列可以无限扩展，即n的值不固定。

（2）匿名认证的正确性证明

可通过式（16）认证示证者Up属于组织U。

证明引理[15]gtmodqmodp=gtmodp。由式（11）、（7）、（9）、（14）、（15）可得：

（3）匿名追踪的正确性证明

可通过式（19）追踪示证者Up的身份，即公钥Sp。

证明由式（18）、（17）、（12）、（7）可得：

3.2 安全性

本文方案的安全性基于对离散对数问题的求解，而离散对数的求解在现阶段是非常困难的。

（1）本文方案具备匿名性

在匿名认证过程中，示证者公开的Ep中并不包含示证者的身份信息，因而，Ep的公开不会泄露示证者的身份。另外，示证者提供的fp中虽然隐含秘密份额的身份信息，但如果想非法获得，就必须求解离散对数问题，而离散对数的求解非常困难。因此，在匿名认证中，示证者的身份满足匿名性。

（2）本文方案具备可追踪性

如果t个成员各自提供正确的Wi，按照式（18）联合计算出Wp，根据式（19）便可恢复出示证者的公钥Sp即身份信息。

（3）本文方案具备门限性质

在系统初始化过程中，由于Ct中含有t个未知数，需要t个方程才能求解出成员的秘密份额；在匿名认证和匿名追踪过程中，Fp和Wp都需要t个成员联合才能计算出来，因而本方案具有门限性质。

（4）本文方案具备完备性

所谓的完备性是指外部成员无法通过匿名认证。在匿名认证过程中，外部成员企图通过认证，就必须提供正确的fi，fi是根据成员的秘密份额si计算得来的，由于离散对数的难解性，外部成员不可能获得秘密份额，因此，外部成员无法通过匿名认证。

（5）匿名认证过程抗伪造攻击

匿名认证过程的伪造攻击可以从两个方面来分析。

①抗示证者的伪造攻击

从式（14）可知，认证成员提供的fi需要使用认证成员的随机数ki'，虽然开始时认证成员的随机数ki是由示证者选择并提供的，但经过匿名认证集合中全体成员的相互协作，认证成员获得了新的秘密随机数ki'，且对示证者是保密的，因此，示证者无法伪造出认证成员的fi。

②抗认证成员的伪造攻击

在匿名认证过程中，由于fi的计算需要使用认证成员自身的秘密份额si，而si是安全保密的，因而认证成员的fi不可能被其他成员伪造出来。

（6）匿名认证过程抗一致性攻击

所谓的一致性攻击是指两次认证是否认证同一个用户。由于每次匿名认证，示证者选择的随机数kp和hp是不固定的，认证成员获得的随机数ki'也是不固定的，因而不能判定两次认证是否是认证同一个用户。

3.3 有效性

（1）协议性质分析

与现有的匿名认证方案进行比较，本文方案同时具有匿名性、门限可追踪性、完备性、抗伪装攻击和一致性攻击，详见表1。

（2）计算代价分析

从表1中可以看出，文献[11]也能实现门限匿名追踪，下面将主要与文献[11]在计算代价上进行比较。为了方便比较，用Tmul代表模乘计算费用，Texp代表模指数计算费用，Th代表哈希函数计算费用，t是门限值，n是成员数，模加/异或运算的时间复杂度相当小，计算费用可以忽略。

文献[11]采用Shamir的Lagrange插值算法计算成员的秘密份额信息，计算的开销是n(t-1)Tmul+n(t-2)Texp，在匿名认证中借鉴民主签名的思想，需要选择2n-1个随机数，计算3n个中间数据xj、yj、zj。本文方案采用线性方程组理论获得成员的秘密份额，计算开销是(t-1)Tmul，在匿名认证中，需要选择t个随机数，计算t个中间数据fi，t个fi进行连乘运算。两种方案的计算代价详见表2。

表2中的数据表明，实现同样功能的情况下，本文方案的计算代价相对较小。

表1 可追踪匿名认证方案性质比较

表2 门限可追踪匿名认证方案计算代价比较

4 结束语

基于线性方程组的求解理论，提出了一种门限匿名认证方案，其安全性依赖于离散对数求解的困难性。与已有的方案相比，本文方案不仅能实现匿名认证，更能实现匿名追踪，且具有门限性质。整个过程中，计算代价相对较小，匿名认证过程相对较简单。在电子商务、移动通信等众多领域，本文方案将具有广阔的应用前景。

[1]Ateniese G，Herzberg A，Krawczyk H，et al.Untraceable mobility orhow to travelincognito[J].ComputerNetworks，1999，31（8）：871-884.

[2]Kong J J，Hong X Y，Gerla M.An identity-free and ondemand routing scheme against anonymity threats in mobile Ad Hoc networks[J].IEEE Transactions on Mobile Computing，Frequency，2007，6：888-902.

[3]Lee C H，Deng X T，Zhu H F.Design and sccurity analysis of anonymous group identification protocols[C]//Proceedings of Pulic Key Cryptography，February 2002，Paris，France.Berlin Heidelberg：Springer-Verlag，2002：188-198.

[4]Eliane J，Guillaume P.On the security of homage group authentication protocol[C]//Proceedings of Cayman Islands，British West Indies，Feb 19-22，2001，2339：106-116.

[5]Xu Z M，Tian H，Liu D S，et al.A ring-signature anonymous authentication method based on one-way accumulator[C]//Proceedings of Communication Systems，Networks and Applications Conference，2010：56-59.

[6]周彦伟，吴振强，蒋李.分布式网络环境下的跨域匿名认证机制[J].计算机应用，2010，30（8）：2120-2124.

[7]宋成，孙宇琼，彭维平，等.改进的直接匿名认证方案[J].北京邮电大学学报，2011，34（3）：62-65.

[8]Hirose S，Yoshida S.A user authentication scheme with identity and location privacy[C]//Proceedings of the 6th Australasian Conference on Information Security and Privacy，Sydney，Australia，July 11-13，2001，2119：235-246.

[9]田子健，王继林，伍云霞.一个动态的可追踪匿名认证方案[J].电子与信息学报，2005，27（11）：1737-1740.

[10]Paik J H，Kim B H，Lee D H.A3RP：anonymous and authenticated ad hoc routing protocol[C]//Proceedings of Information Security and Assurance Conference，2008.

[11]刘方斌，张琨，李海，等.无可信中心的门限追踪Ad Hoc网络匿名认证[J].通信学报，2012，33（8）：208-213.

[12]石润华，仲红，黄刘生.公开可验证的门限秘密共享方案[J].微电子学与计算机，2008，25（1）：29-33.

[13]殷凤梅，濮光宁.允许新成员加入的无可信中心秘密共享方案分析[J].重庆科技学院学报：自然科学版，2011，13（6）：173-175.

[14]张清华.基于密钥交换中离散对数生成元的研究[J].重庆邮电学院学报，2002，14（3）：90-92.

[15]Harn L.Efficient sharing（broadcasting）of multiple secrets[J].IEE Proc Comput Digit Tech，1995，142（3）：237-240.