认知无线电中基于比例公平的资源分配方案

周刘纪，刘开华，马永涛

天津大学 电子信息工程学院，天津 300072

1 简介

认知无线电（Cognitive Radio，CR）作为一种能够有效提高频谱利用率的无线通信技术[1]，可以检测频谱空洞并在不影响授权用户网络通信质量的情况下为次用户网络提供接入服务。为了衡量次用户对授权用户通信的干扰程度，文献[2]提出了认知无线电网络中干扰温度的概念，当次用户和授权用户共享同一段频谱时，次用户对授权用户的干扰必须限制在一定范围内，否则将不能保证授权用户的通信服务质量（Quality of Service，QoS）。

协作通信[3]是一种能够有效对抗信道衰落，增加系统吞吐量的空间分集技术，协作技术应用在认知无线电网络中可以提高资源分配的公平性和系统吞吐量[4]。研究表明，采用OFDM调制技术会因为信号的非正交性而导致授权用户与认知用户发送端在通信过程中相互干扰，经典的功率分配算法（例如贪婪算法和注水算法）会对授权用户造成较大的干扰。因此，在不影响授权网络通信性能的前提下，研究资源分配具有很高的实用价值。

在协作通信中，关于功率分配的研究[5-9]都假定中继用户是专门用来辅助其他用户进行数据转发的，但一些如蜂窝通信等无线网络，每个用户都需要传输自己的数据，不能把用户发送端充当纯中继作用，在不影响用户发送自己数据的同时协助其他用户发送数据[10]是关切问题。通过最大化最小速率（maximize-worst）可以提高用户资源分配公平性，该准则把过多资源分配给了性能差的用户，会降低系统的传输效率。

文献[11-12]提出在各子载波上的发射功率进行均分（EPA）来提高用户资源分配的公平性。文献[13]在此基础上提出了EPA-PRG（Proportional Rate Greedy）算法，该算法能够在满足用户资源分配公平性的前提下提高系统的吞吐量而不增加算法复杂度。文献[14]考虑到了公平性却没有解决功率分配问题；文献[15]在确保次级用户公平性的前提下提出了最大化系统容量的资源分配算法。这些算法均没有考虑到对授权用户的干扰。

针对以上算法的不足，本文提出了基于OFDM的功率和子载波分配及配对算法（OFDM-PASA），研究的系统传输模型中，协作用户之间通过放大转发（AF）协作模式进行数据传输，利用空间分集技术提高资源分配有效性，在对本文算法求解过程中采用迭代梯度法逼近求解性能函数以获得的最优解。

2 系统模型

2.1 基于OFDM-AF的认知无线网络传输模型

图1 认知用户基于协作的系统传输模型

如图1所示，由一个授权用户发送端（Primary Transmitter，PT）和一个授权用户接收端（Primary Receiver，PR）组成的授权网络拥有一段已授权的频谱。由K个次级用户发射端（Secondary Transmitter，ST）和一个次级用户接收端（Secondary Receiver，SR）组成的认知系统没有分配到频带，只能共享授权用户的频谱进行信息传输。假定每个ST已经分配好固定的ST进行协作传输，例如协作组k中，ST1与ST2互为中继进行数据传输。

授权用户和认知用户的频谱分配情况如图2所示[16]。授权用户占用频段带宽为B，ST通过频谱感知技术能够感知到被授权用户占用的频带，并检测出其他可使用的空闲频谱资源，这些可用频谱被均匀分成N个子频带，子频带的带宽设为Δf。

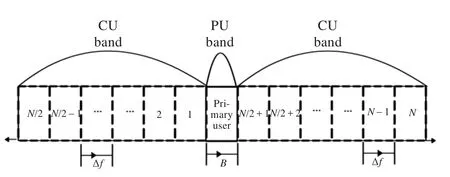
图2 认知无线电频谱接入模型

认知协作组k中，STi利用子载波n进行数据传输时对授权频带所造成的干扰为[17]：

式中，Ts表示一个OFDM符号的持续时间；i=1，2表示认知协作组k中STi在子载波n上到PR的信道衰落系数，dn表示第n个子载波与授权频段间的距离。由式（1）可知距PU频段越近，载波对PU产生的干扰越大，为方便分析，本文仅考虑次级网络对授权网络的干扰。

ST以连续的帧进行数据发送，如表1所示，发送第t帧数据时，T1时隙ST1通过子载波n以的功率因子将数据x1(t)广播到SR以及ST2，ST2把所接收到的数据放大为，并在T2时隙通过子载波E(n)以功率因子把数据转发到SR。发送第t+1帧数据时ST1与ST2的数据发送顺序相互交换，即在T1时隙ST2通过子载波n以的功率因子将信息x2(t)广播到SR和ST1，ST1把所接收到数据放大为(t+1)，T2时隙通过子载波E(n)，以功率因子把放大后的数据(t+1)转发到SR。

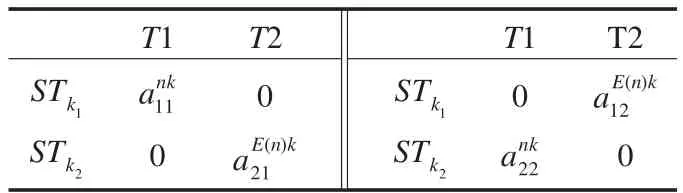
表1 功率分配因子

以协作方式进行数据传输过程中，ST以子载波n广播到中继ST的数据，中继ST以子载波E(n)进行转发，即E(n)表示与子载波n配对的子载波。认知协作组k中STi在子载波n上向STj发送数据的功率因子用表示。ST各时隙的功率因子分配如表1所示，本文假设所有ST的最大发送功率相等，即==P。

[18]，认知协作组k中ST1和ST2在子载波n上的所能达到的最大数据传输速率可以表示为：

式中，表示STi到STj的信道衰落系数，SR节点用“0”表示，为有效信道增益，为源节点子载波n发射功率，为中继节点时子载波n发射功率。认知协作组k中，STi在第n个子载波上所加的噪声是均值为0，方差为Nink的高斯白噪声。一般情况下，通过AF中继的信号都具有较高的信噪比，因此，式（2）分母中“1”可忽略，进而简化为式（3）：

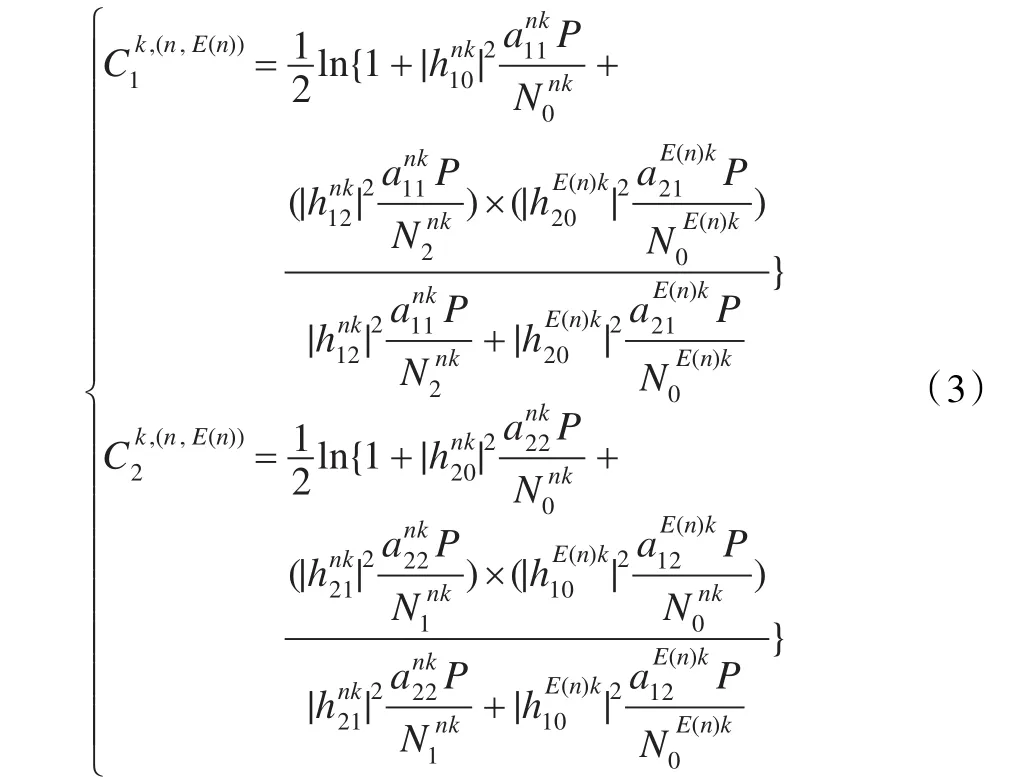
次级网络采用OFDM调制技术，分配给各协作用户组进行数据传输的子载波互不重叠，因此各ST发送的信号不会相互干扰。为了提高认知用户资源分配的公平性以及提高系统数据传输效率[3]，需要为ST分配最优子载波并为各子载波进行配对，同时还需要对各子载波上的发射功率进行优化。

2.2 基于OFDM-AF功率和子载波分配方案

令ρkn表示子载波分配因子，只有当子载波n被分配到认知协作组k时ρkn=1，否则令ρkn=0，(1≤k≤K，1≤n≤N)。为了使ST->SR通信过程中对授权用户造成的干扰低于门限值Ith，ST的发送功率必须满足以下约束不等式：

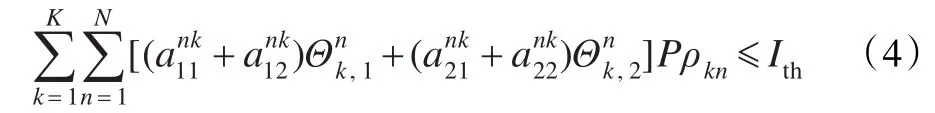
用户在进行通信的过程中数据传输速率必须大于一定值，否则无法满足正常通信所要求的数据率。多用户的认知无线电系统中，需要公平性地为ST分配功率及子载波资源。

综上所述，功率及子载波分配方案可用如下数学方程进行描述：

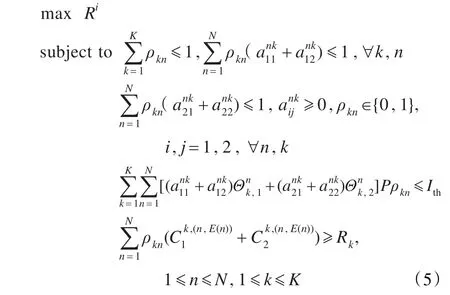
目标函数Ri是根据系统的优化目标而定，可以是以提高系统传输效率为目的的maximize-total优化目标函数，也可以是以提高用户资源分配公平性为目的的maximize-worst优化目标函数。本文的研究是使这两个指标得到平衡，采用比例公平maximize-pro-fair优化目标函数；式中Rk表示第k组ST->SR能正常进行通信的最低数据传输速率。优化目标可以是提高系统传输效率、用户资源分配公平性，效率与公平性兼顾，因此目标函数Ri表述为：

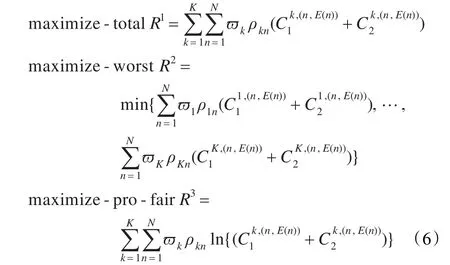
3 功率和子载波分配及配对方案

式中λ1n，λ2k，λ3k，λ4，λ5k为拉格朗日乘法因子。提取出具有分配因子、ρkn的项，可以得到K个不等式方程：

假设式（8）的最大值为Ψk，则优化模型（7）的剩余项为：

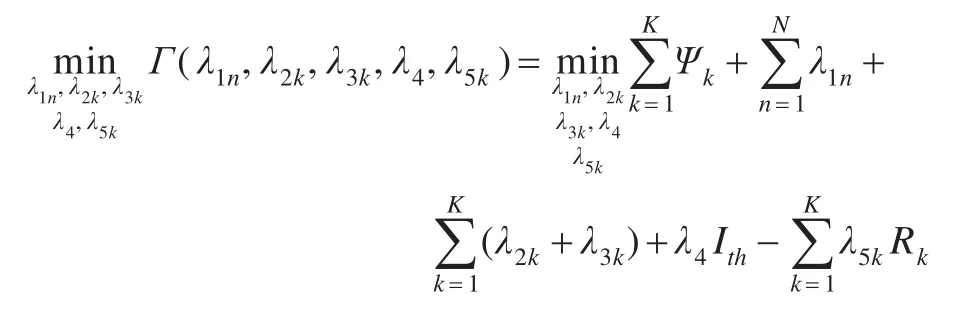
3.1 协作方式下的功率因子分配

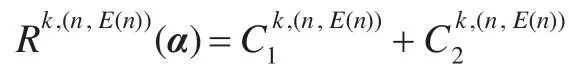
由式（10）解得：

将式（12）分别代入式（11）可得：

由式（11）和式（13）求得最优功率分配因子：

上式表明，如果没有为协作用户分配功率，认知用户发送端的功率分配问题退化为多级功率灌水问题。

3.2 分配用于协作的最优子载波集

式中ζ表示权重值，ζ越大表示资源分配过程中资源分配准则越偏向于提高公平性，反之偏向于提高系统传输速率。式（15）中由于存在ρkn∈{0，1}，是一个混合二进制整数优化问题，由函数

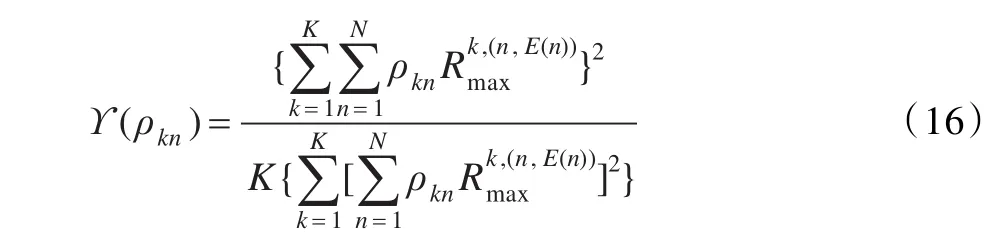
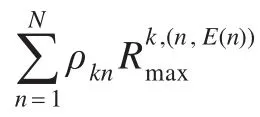
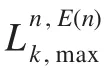
为协作用户分配最优子载波集的算法流程为：

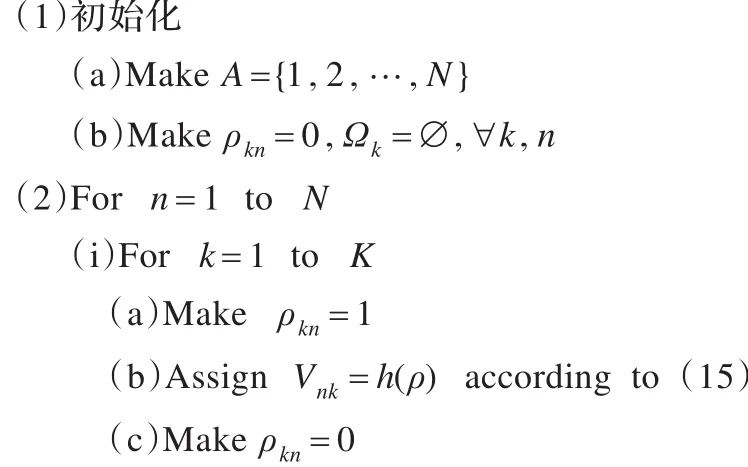
3.3 为最优子载波集进行配对

令βn，j表示子载波配对因子，当子载波n与子载波j配对时令βn，j=1，否则令βn，j=0 。在为ST分配好用于协作的最优子载波集Ωk后，协作用户ST以子载波n发送到中继ST的数据，中继需要选择最优的子载波E(n)并通过子载波E(n)把这些数据转发到目的接收端SR，通过子载波的优化配对可以提高系统传输效率。认知协作组k中子载波配对过程可以表示为：

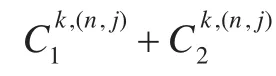
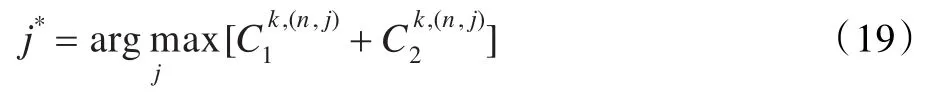
则这个子载波j*与子载波n配对，即：

为ST分配好用于协作的最优子载波集后，子载波配对的算法流程可以描述为：

3.4 优化对偶变量

其拉格朗日乘性因子可按以下梯度迭代公式进行更新：

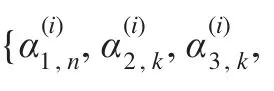
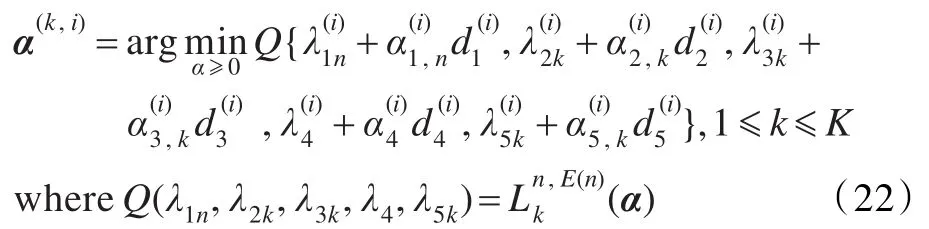
3.5 算法比较

算法1功率均分-子载波分配（Equal Power Allocation versus Subcarrier Allocation，EPA-SA），该算法下各子载波上的功率进行平均分配以提高用户资源分配公平性，但子载波按照本文所提子载波分配算法进行分配并配对。

算法2功率分配-子载波未分配（Power Allocation versus Subcarrier Non-Allocation，PA-NSA），采用文中所提功率分配算法对各子载波发送功率进行优化分配，但子载波分配是根据发射端（ST）到接收端（SR）的信道增益大小进行分配及配对的。

算法3功率均分-子载波未分配（Equal Power Allocation versus Subcarrier Non-Allocation，EPA-NSA），该算法下对各子载波上的发射功率进行平均分配，子载波按照各发射端（ST）到接收端（SR）信道增益大小进行分配及配对。

4 仿真结果与分析

在对本文OFDM-PASA功率及子载波分配算法进行实验仿真过程中，运用到了凸优化和CVX程序包，假设认知系统中所有信道都是瑞利衰落信道，衰落系数，i={1，2}，j={0，1，2}，∀n，k是均值为0，方差为1的独立复高斯随机变量。在分析比较频谱资源和功率分配的公平性时，使用公平测度函数[22]来反映资源分配的公平性：

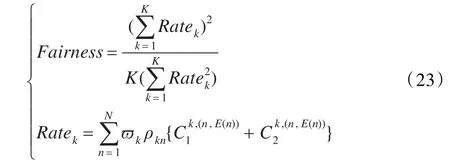
运用Matlab软件对本文OFDM-PASA资源分配及配对算法进行仿真，并将本文所提资源分配算法与其他资源分配算法进行对比分析。仿真过程参数设置如下：Ts=4 μs，Δf=0.312 5 MHz，B=0.312 5 MHz，子载波数N=10，认知用户组数K=2，进行10 000次蒙特卡洛测试。

图3表明系统吞吐量随信噪比增加而增加，因为信道所能传输的信息量随着信噪比的增大而增加。从图中可以看出，OFDM-PASA资源分配方案下系统所能获得的传输速率最高。与PA-NSA、EPA-SA资源分配方案相比，当系统传输速率一定时，认知用户采用OFDM-PASA资源分配方案能够获得1～2 dB的协作增益，与表现最差的EPA-NSA分配方案相比，能提高2.5 dB的协作增益。

图3 各分配方式下系统Rate-SNR曲线

图4表明在不同资源分配方案下认知用户的公平性均随信噪比的增大而增加，因为信噪比越高，各协作用户组在提高数据发送速率的能力上是相当的。通过对比用户在不同分配方案下所能达到的公平性可知，当信噪比一定时，用户资源分配的公平性是按照EPA-NSA、PA-NSA、EPA-SA、OFDM-PASA顺序递增的。EPA-NSA分配方案下认知用户资源分配公平性是最低的，而且公平性曲线的浮动比较大，OFDM-PASA方案下用户所能达到的公平性是最高的且稳定度也是最好的，OFDM-PASA和EPA-SA资源分配方案中均采用本文优化函数对子载波进行了优化分配及配对，由于EPA-SA方案中没有对认知用户发射端功率进行协作分配，因此在该分配方案下用户资源分配公平性不高，PA-NSA方案下ST虽然在各子载波上发送功率进行了协作分配，但并没有采用本文算法对各子载波进行分配及配对，而仅仅根据信道增益大小进行分配，因此PA-NSA的性能曲线也较OFDM-PASA差。

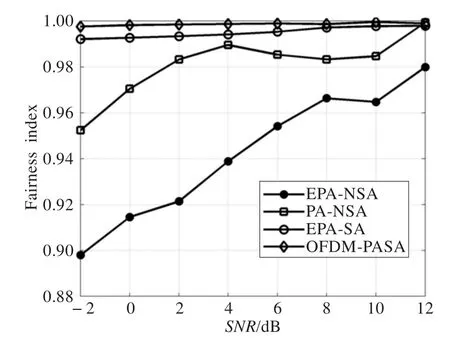
图4 各分配方式下系统Fairness-SNR曲线

图5 单组SU用户下的Fairness-SNR曲线

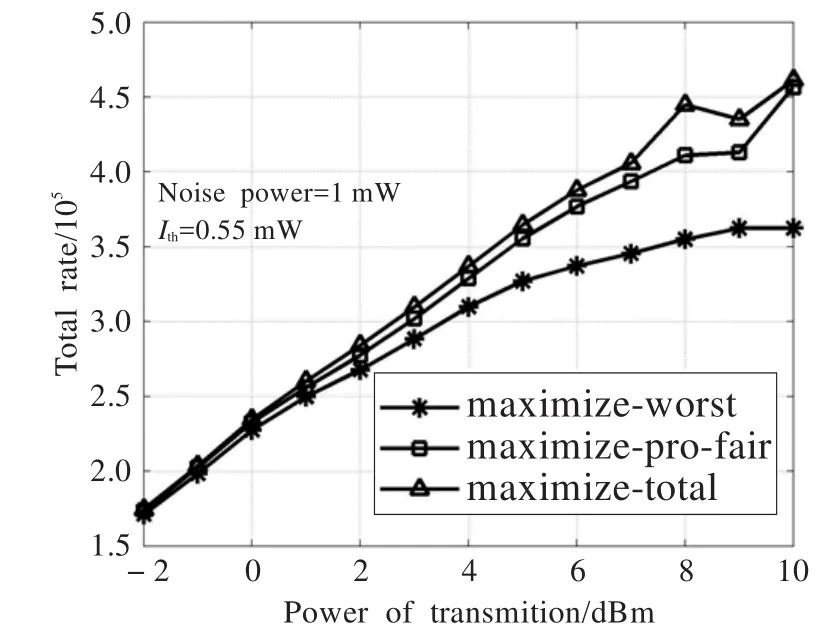
图6 单组ST下的Rate-SNR曲线

通过对图5和图6进行比较分析可以看出，maximize-worst测度函数以最大化最差的ST速率为优化目标，因此在最大最小优化函数下认知网络系统传输效率最差但资源分配的公平性最高。在maximize-pro-fair优化函数下用户资源分配的公平性和认知网络系统的传输效率在三者中都处于中间，这说明采用maximize-pro-fair目标优化函数可以很好地权衡系统传输效率与用户资源分配公平性的关系，同时还能满足各用户的通信性能要求，采用maximize-total测度函数系统所获得的吞吐量最大，但所获得的用户公平测度最小。

如图5所示，随着信噪比的增加，maximize-worst和maximize-pro-fair优化目标函数的公平性均有所下降，而maximize-worst目标函数的公平性基本保持在“1”不变。这是因为在信噪比大的时候，各ST均能获得较好的数据传输率，考虑到提高认知网络系统吞吐量，此时资源分配较偏向于能最大化系统吞吐量的用户。当信噪比较小时，ST->SR的通信性能不能完全满足要求，此时资源分配较偏重于使各ST均能达到最低数据传输率，此时用户分配的资源公平性较高。随着信噪比的增加，公平测度曲线趋于稳定，用户所获得的传输效率提升幅度相当。

随着信噪比的增大，各优化目标函数下的系统传输效率均能得到大幅提高，如图6所示。且在优化目标函数maximize-total下的系统传输效率始终是最高，在比例公平maximize-pro-fair目标函数下，系统的传输效率处于中间水平，但maximize-total与maximize-pro-fair所获得的系统吞吐量的差别很小，几乎可以忽略。总体来说，本文使用的maximize-pro-fair目标函数能够平衡系统吞吐量与认知用户资源分配公平性这两个指标。

5 结束语

提出了基于OFDM的功率分配和最优子载波分配及配对算法OFDM-PASA，与已有的资源分配算法不同，本文把用户协作发送数据的思想运用到认知无线电系统中，同时考虑了参与协作转发数据的中继用户也需要发送自己的数据，认知协作用户相互充当对方的中继进行数据转发；提出以比例公平maximize-pro-fair测度函数作为优化目标。仿真结果证明，maximize-pro-fair测度函数可以使系统传输效率和用户资源分配公平性这两个指标得到均衡。本文所提的资源分配算法对认知用户发送端的子载波进行了最优化分配及配对，并对其功率因子进行了优化，因此相比其他算法，所提的算法无论在系统吞吐量还是认知用户资源分配的公平性方面都具有很好的效果，仿真结果也证明了本文算法的优越性。

参考文献：

[1]Haykin S.Cognitive radio brain-empowered wireless communications[J].IEEE Journal on Selected Areas in Communications，2005，23（2）：201-220.

[2]Xing Yiping，Mathur C N，Haleem M A，et al.Dynamic spectrum access with QoS and interference temperature constraints[J].IEEE Transactions on Mobile Computing，2007，6（4）：423-433.

[3]Laneman J N，Tse D N C，Wornell G W.Cooperative diversity in wireless networks：efficient protocols and outage behavior[J].IEEE Transactions on Information Theory，2004，50（12）：3062-3080.

[4]Liang Y，Veeravalli V V，Poor H V.Resource allocation for wireless fading relay channels：Max-min solution[J].IEEE Transactions on Information Theory，2007，53（10）：3432-3453.

[5]Yang Dejun，Fang Xi，Xue Guoliang.HERA：an optimal relay assignmentscheme forcooperative networks[J].IEEE Journal on Selected Areas in Communications，2012，30（2）：245-253.

[6]Liu Jia，Shroff N B，Sherali H D.Optimal power allocation in multi-relay mimo cooperative networks：theory and algorithms[J].IEEE Journal on Selected Areas in Communications，2012，30（2）：331-340.

[7]Kim K，Shin Y.An improved power allocation scheme using particle swarm optimization in cooperative wireless communication systems[C]//Proceedings of the 17th Asia-Pacific Conference on Communications，2011：654-658.

[8]Oberoi J S，Pareek U，Naeem M，et al.EDA-based joint power，subcarrier allocation and relay assignment scheme for multiuser relaying in OFDMA-based cognitive radio systems[C]//Proceedings of the 5th International Conference on Signal Processing and Communication Systems（ICSPCS），2011：1-7.

[9]Ashrafinia S，Pareek U，Naeem M，et al.Source and relay power selection using biogeography-based optimization for cognitiveradio systems[C]//Proceedingsof2011 IEEE Vehicular Technology Conference（VTC Fall），2011：1-5.

[10]Tourki K，Gesbert D，Deneire L.Cooperative diversity using per-user power control in the multiuser mac channel[C]//Proceedingsof2007 IEEE InternationalSymposium on Information Theory，2007：1911-1915.

[11]Maciel T F，Klein A.On the performance，complexity，and fairness of suboptimal resource allocation for multiuser MIMO-OFDMA systems[J].IEEE Transactions on Vehicular Technology，2010，59（1）：406-419.

[12]Papoutsis V D，Fraimis I G，Kotsopoulos S A.User selection and resource allocation algorithm with fairness in MISO-OFDMA[J].IEEE Communications Letters，2010，14（5）：411-413.

[13]Lu Weishan，Ji Fei，Yu Hua.General resource allocation algorithm with fairness for SDMA/MISO/OFDMA systems[J].IEEE CommunicationsLetters，2011，15（10）：1072-1074.

[14]Papoutsis V D，Fraimis I G，Kotsopoulos S A.Fairnessaware user selection and resource allocation in MISOOFDMA[J].European Transactions on Telecommunications，2010，21（6）：567-573.

[15]Mohanram C，Bhashyam S.A sub-optimal joint subcarrier and power allocation algorithm for multiuser OFDM[J].IEEE Communications Letters，2005，9（8）：685-687.

[16]Tang Lun，Hu Lin，Wang Huan，et al.Power allocation based on convex optimization theory for fading channels in OFDM-based cognitiveradio networks[C]//Proceedings of 2009 International Conference on Wireless Communications&Signal Processing，2009：1-5.

[17]Weiss T，Hillenbrand J，Krohn A，et al.Mutual interference in OFDM-based spectrum pooling systems[C]//Proceedings of IEEE 59th Vehicular Technology Conference.[S.l.]：IEEE，2004：1873-1877.

[18]卢为党，吴宣利，沙学军，等.基于OFDM协作中继的机会主义频谱共享协议及其最优资源分配[J].通信学报，2012，33（11）：74-83.

[19]Yin R，Zhang Y，Yu G D，et al.Centralized and distributed resource allocation in OFDM based multi-relay system[J].Journal of Zhejiang University：Science C Computers&Electronics，2010，11（6）：450-464.

[20]Yong L，Wang W B，Kong J，et al.Power allocation and subcarrier pairing in OFDM-based relaying networks[C]//Proceedings of IEEE International Conference on Communications.[S.l.]：IEEE，2008：2602-2606.

[21]Wei Y，Lui R.Dual methods for non-convex spectrum optimization ofmulticarriersystems[J].IEEE Transactions on Communications，2006，54（7）：1310-1322.

[22]Papoutsis V D，Fraimis I G，Kotsopoulos S A.User selection and resource allocation algorithm with fairness in MISO-OFDMA[J].IEEE Communications Letters，2010，14（5）：411-413.