基于金字塔凸壳算法的初始凸包快速优化算法①

张忠武，周 宇，孟祥华，肖 永

(佳木斯大学建筑工程学院，黑龙江 佳木斯154007)

0 引 言

凸包作为计算几何研究当中重点解决的问题之一，当前许多理论问题与实际问题都需要凸包作为重要的解决工具.如地理信息系统中进行区裁剪、洪水淹没区域范围确定等应用都将应用到凸包算法.因此凸壳问题特别是平面点集的凸壳更加得到学术界的重视与关注.凸包问题主要是获取点集的最外围顶点，但一般情况下凸包顶点只是海量数据点集的极小一部分，凸壳内部包含了大量对凸壳生成无用的非凸壳顶点.所以可采用尽可能多删除不包含在凸壳边界上的非凸壳顶点的方法，减少数据点集数量进而提升凸壳算法的执行效率，这种方法被称为快速凸包技术［1］.Floyd 四边形法以及余翔宇编写的八边形法就是基于快速凸包技术所提出的凸壳算法，两种算法都是将海量数点集预先进行处理，剔除不能作为凸壳顶点的凸壳内点［2］.从理论上来说快速优化技术不能降低凸壳算法的时间复杂度，可是实际当中数据大多呈现正态分布，多数情况下快速优化算法对提升实际的执行效率有很大帮助.结合传统的凸包算法提出了金字塔凸壳算法，其算法步骤与特点适合将快速优化技术结合进来.本文将快速优化算法改造成适应金字塔算法的初始近似凸壳算法，便于其在金字塔凸壳算法中实现，降低平面点集中非凸壳顶点数量，提升整体算法实际运行效率.

1 初始近似凸壳算法的工作原理

初始近似凸壳算法是基于传统快速凸包技术改进而来的，其工作原理同样是用最少的时间代价事先剔除不能作为顶点的尽可能多的凸壳内点，从而达到提升金字塔算法的实际时间效率.初始近似凸壳算法的基本思想是首先在点集S 中查找获取横坐标数值最大、最小与纵坐标数值最大、最小的4 个方向的极值点，再将4 个极值点连接起来构成最小外接矩形PLPBPRPT.如果横纵坐标轴方向上的极值点不只4 个，可取各自方向的任意点作为最值点.这对后期使用金字塔凸壳算法无影响，这源自于金字塔凸壳算法的基本思想［3］.至此已将平面离散数据点集S 划分成五部分:Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，见图1.点集Ⅴ所含数据点一定是非凸壳顶点，不可能用于生成凸包的凸壳顶点;另外点集Ⅰ，Ⅱ，Ⅲ，Ⅳ它们彼此之间无交叉数据点相互独立，每个点集上的数据点能否作为凸壳顶点都由各自点集中点的位置决定，和其他点集中的数据点无关联，同时各点集中的凸壳顶点必是整个点集的顶点，为此这四个点集的凸壳顶点获取方法相同，可以采用金字塔算法寻找四个点集的凸壳顶点，最后将这些凸壳顶点顺次连接成所求得整个点集的凸包.

2 初始近似凸壳算法的实现

遍历点集中所有点查找横纵坐标四个方向相应的极值点，连接四个方向上极值生成4 条有向线段PL→PT、PR→PT、PL→PB、PR→PB将平面数据点集S 划分成五个区域［4］.然后根据判断点线位置关系的行列式值大小判断平面数据点集中所有点归属哪个子点集，具体判断方法如下:逐个选取平面数据点集中的点进行判断，若点位于有向线段PL→PT左侧，则该点属于点集Ⅰ;若点位于有向线段PR→PT右侧，则该点属于点集Ⅱ;若点位于有向线段PL→PB右侧，则判定该点归属于点集Ⅲ;若点位于有向线段PR→PB左侧，则点将作为点集Ⅳ中的点;否则，该点属于点集Ⅴ.当判定所有点归属之后，分别只对Ⅰ、Ⅱ、Ⅲ、Ⅳ点集中的数据点采用金字塔算法求出相应各子集的凸壳顶点，之后再将各子集的凸壳顶点顺次连接生成整个平面数据点集的凸壳.具体步骤如下:

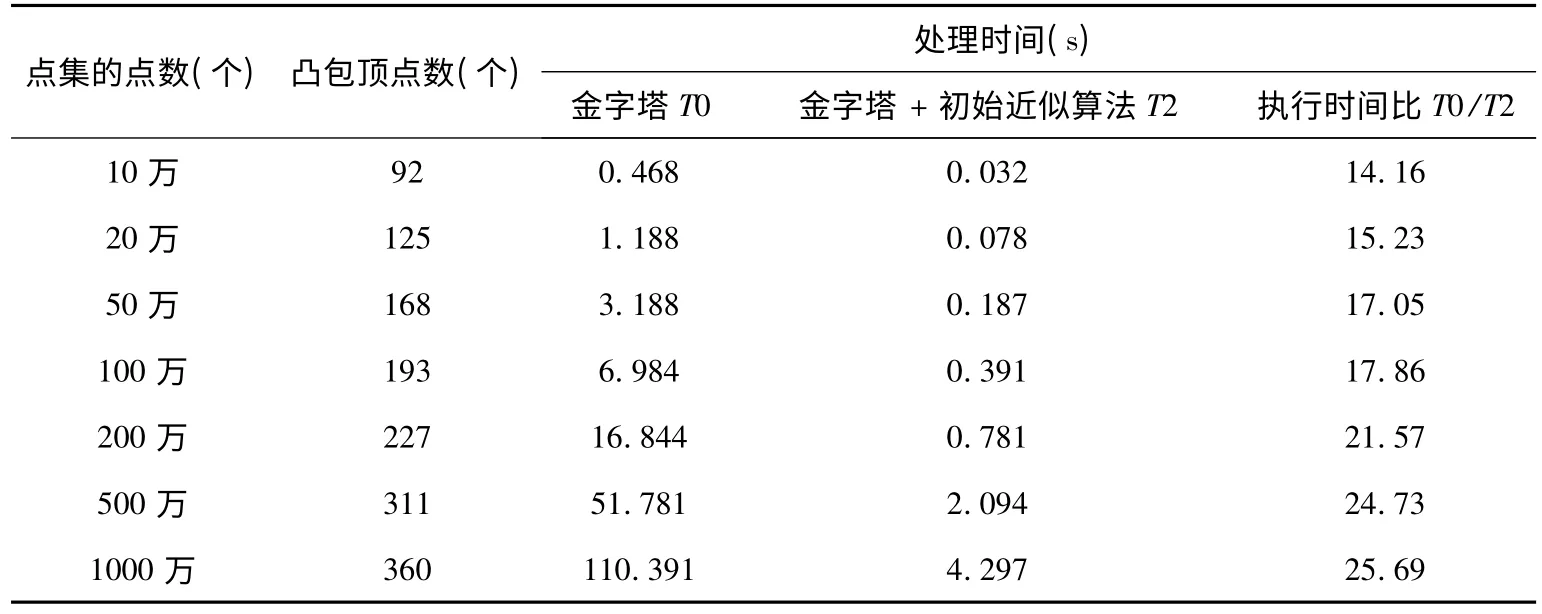
表1 初始近似凸壳算与金字塔算法相结合的测试数据

步骤1 查找点集横纵坐标上四个方向的极值点，当各方向上含有多个极值点时任选一个，再将四个极值点进行有向连接，生成四个各有向线段PL→PT、PR→PT、PL→PB、PR→PB;

步骤2 循环判定点集中各点与各条有向线段的位置关系，进而确定该点属于Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ哪个子集;

步骤3 对Ⅰ、Ⅱ、Ⅲ、Ⅳ每个子集中的点，分别采用金字塔凸壳算法查找出各自子集中的凸包顶点，见图2，再将其将顺次连接生成最终凸包;

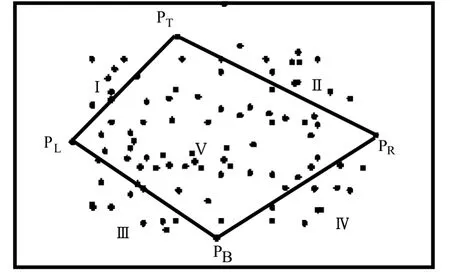
图1 近似的粗凸包对平面点集的划分

3 算法的加速效率分析

根据对初始近似凸壳算法实现步骤进行分析可知，步骤1 与步骤2 分别需要进行n 次的循环，时间复杂度为(n)，所以初始近似凸壳算法加速优化效率的好坏主要取决于删除非凸壳顶点后，平面数据点集的规模与凸壳顶点个数，其中顶点个数是不变的，因此主要取决于点集规模.在步骤3 中各点集都采用金字塔算法，若剔除后点集规模为m、顶点数为k，步骤3 的时间复杂度为O(1/4km).为验证初始近似凸壳算法的加速优化效率，笔者进行大量实验，具体实验数据见表1.对表1 的实验数据分析可知，初始近似凸壳算法提升金字塔凸壳算法的执行效率14 ～25 倍，同时凸包内点越集中、越密集时，其加速优化效率越明显.

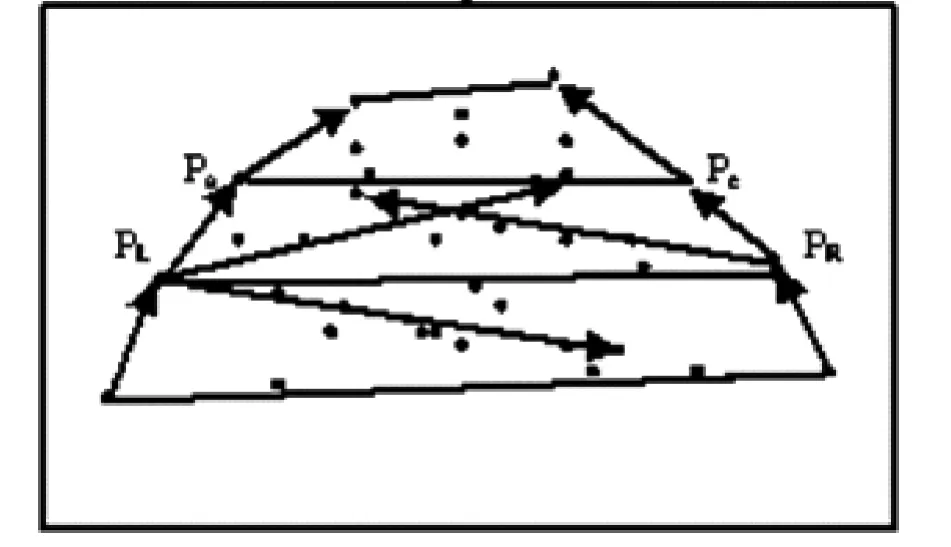
图2 子集凸壳顶点生成过程

初始近似凸壳算法加速效率取决于点集划分时，点集V 中含有多少不参与凸壳顶点判断的点的数据量.为提升初始近似凸壳算法的加速优化效率笔者还采用余翔宇编写的八边形法凸包快速算法，由八个极值点构成的凸八边形作为点集近似凸包，目的是将更多点集划分到凸壳内点集中提升初始近似凸壳算法的加速优化效率.但是实际试验结果证明整个算法的运行效率没有明显提升，实验数据见表2.通过分析得知其原因在于平面点集中多数呈现正态分布内点多集中在中央，所以采用八边形和四边形作为初始粗凸包对提高算法执行效率区别不大.并且在步骤1 和步骤2 当中增加了判断比较次数降低了执行效率，所以初始近似凸壳算法和金字塔算法相结合时，不是近似凸包的边数越多执行效率越好，而是由前面论述凸四边形作为初始近似粗凸包效果最佳.

4 结束语

本文结合金字塔凸壳算法和Floyd 四边形法快速算法的特点，提出改造一种快速凸壳算法(初始近似凸壳算法).改造之后的初始近似凸壳算法根据其自身特点，它归属于静态加速算法，所以该加速优化算法只需在初始阶段用很少的时间代价删除平面数据点集中的凸壳内点，即可大幅提升整个凸壳算法的执行效率.通过试验结果分析得出初始近似凸壳算法在选定初始粗凸包时，并不是粗凸包边数越多执行效率越佳，恰相反初始粗凸包选择四边形执行效果最佳.

［1］ 余翔宇，孙洪，余志雄.改进的二维点集凸包快速求取方法［J］.武汉理工大学学报，2005，27(10):81－83.

［2］ 吴克勤，杨冠杰.空间点集卷包裹算法的优化实现［J］.青岛海洋大学学报，2003，33(4):627－633.

［3］ 张忠武，吴信才.平面海量散乱点集凸壳算法［J］.计算机工程，2009，35(9):43－45，48.

［4］ 金文华，何涛等.基于有序简单多边形的平面点集凸包快速求取算法［J］.计算机学报，1998，21(6):533－539.