关于非线性退化时滞微分方程解的研究①

王 健，张志信，蒋 威

(安徽大学数学科学学院，安徽 合肥230601)

0 引 言

近年来，控制系统引起了国内外许多学者们的广泛研究.在控制系统是否稳定和稳定时对其解是否可控制的方面正吸引着许多学者们孜孜不倦的探索着.虽然现在已经在系统稳定性［1～4］的研究上取得了丰硕的重要的成果，但都只是在常微分系统的稳定性问题上，而关于退化的时滞微分系统的研究中，结果相对较少，而时滞现象普遍存在于实际系统中，是我们在系统建模时必须要考虑的重要因素之一.目前关于退化时滞微分方程的研究已引起了学者们的广泛关注，并取得了一定的理论成果［5～8，10～16］，而且随着科技发展和实际建模的复杂性提高，退化时滞微分系统广泛的用于控制系统，管理系统，工程系统，金融分析系统等许多科学和工程系统中，所以研究这类退化时滞微分系统具有十分重要的实际意义.本文在已有研究成果的基础上，研究了含有退化和时滞现象的非线性系统的解的估计问题，所研究的非线性系统具有很重要的理论和实际应用价值.

在文献［7］中讨论了对退化多时滞微分系统:

作者在系统是正则的条件下给出解的存在性和指数估计的充分条件.

文献［8］对退化中立型退化多时滞微分系统:

作者给出了此系统解的存在性和指数稳定问题.

本文主要讨论了如下非线性退化时滞微分系统的解的存在性和指数估计问题

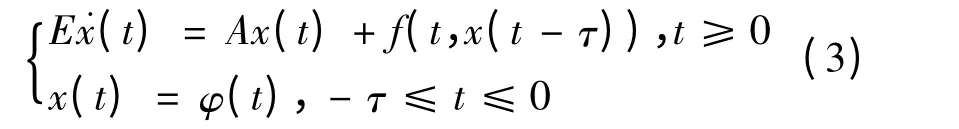
其中E ∈Rn×n，E ≠0，|E|=0，τ ＞0，矩阵对(E，A)是正则的，x(t)，φ(t)，f(t，x(t－τ))∈Rn，且有x(t)，f(t，x(t－τ))在(t ＞0)上是连续函数，并且φ(t)，f(t，x(t－τ))是有界函数.

1 预备知识

定义1.1 对矩阵对(E，A)，若存在不全为零的常数λ 使得det(λE+A)不恒等于0，则称(E，A)是正则的.若det(λE+A)不恒等于常数，则称矩阵对(E，A)是严格正则的.

引理1.1［9］系统

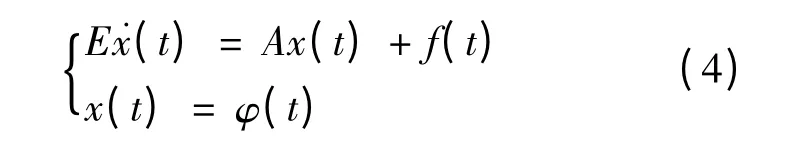
的解存在唯一的充要条件是矩阵对(E，A)是正则的.

引理1.2［9］如果矩阵对(E，A)是正则的，则存在可逆矩阵P，Q 使得

其中n1+n2=n，In1和In2分别是n1，n2阶单位矩阵，Nn2是n2阶幂零矩阵.

引理1.3［10］Gromwell 不等式，若u(t)，α(t)都是［a，b］上连续的实函数，β(t)≥0 在［a，b］上可积，α(t)非减，且有:

则必有:

引理1.4［11］设D 为微分算子，N 为幂零矩阵，则算子(ND－I)－1存在且为有界线性算子.

2 解的存在性

定理1: 若系统(3)是正则的，则存在满足初始条件的解x(t)(t ＞0).

证明: 因为矩阵对(E，A)是正则的，所以存在可逆矩阵P，Q 使得，其中A1是n1维的，并且n1+n2=n，这里令所以系统(3)就化为:

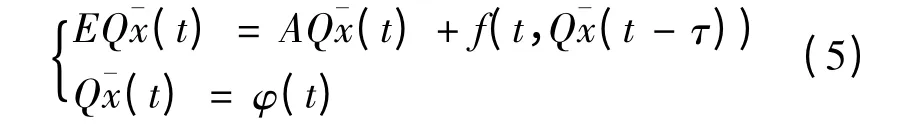
(5)方程的两边得到方程:

是可逆的矩阵)所以(6)和(5)是同解的.

b)对(6)第二个式子首先考虑t ∈［0，τ］时，

d)在区间［τ，2τ］上，利用b)中的方法在由a)和b)可得解(t)，(t ∈［τ，2τ］)也是存在且唯一的;

e)在其他区间［iτ，(i+1)τ］，(i ＞1)上，由上诉的方法类似证明可知方程的解是存在且唯一的，综上所述可知，当t ≥0 时(6)的解是存在的，即系统(3)解是存在的.

证毕.

3 解的指数估计

定理2: 设x(t)为(3)的解，若系统(3)是正则的，且有界连续函数g(t，x(t－τ))满足Lipchitz条件的，则存在正常数a，b，使得:x(t)≤aebt

证明: 下面考虑系统(3)的等价方程(6)，

a)对方程(6)第一个式子两边同时积分0 →t，由于

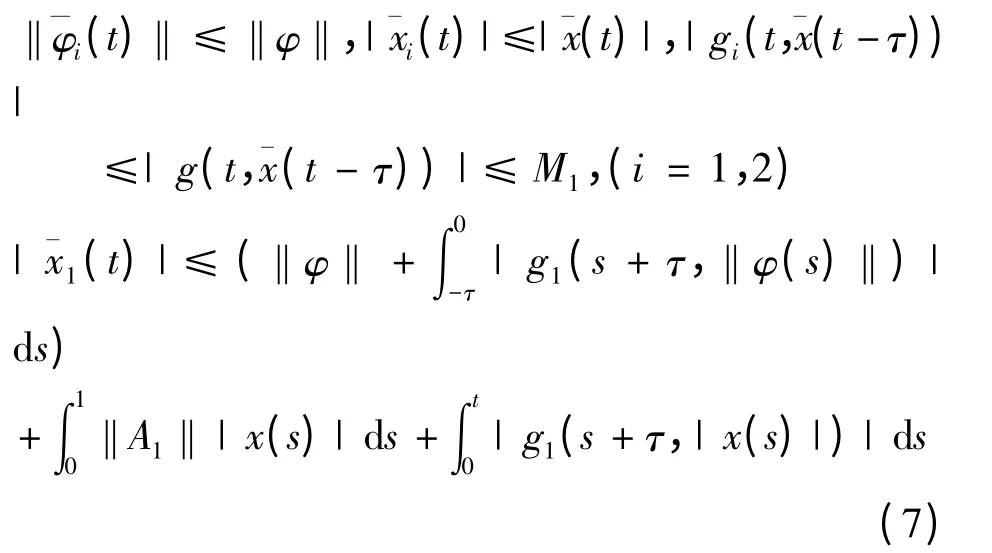
b)对(6)第二个方程，在0 ≤t 时，

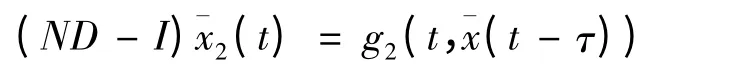
由引理2.4 可知(ND－I)是可逆的有界算子，设|(ND－I)|－1|≤M2，(M2＞0)，所以上式可化为:

联立(7)和(8)式得:

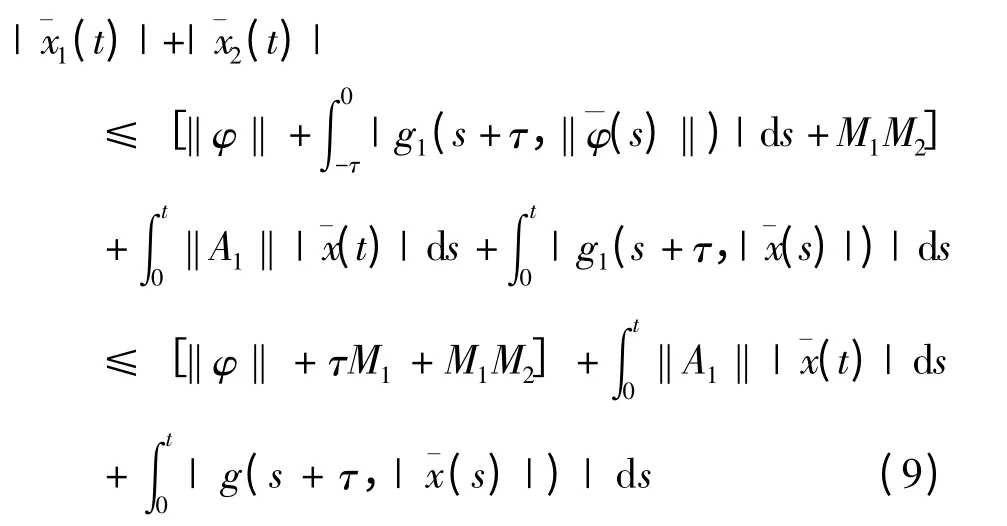
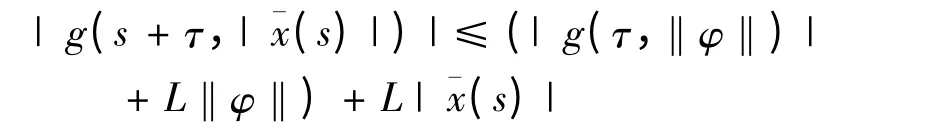
则(9)式变为:

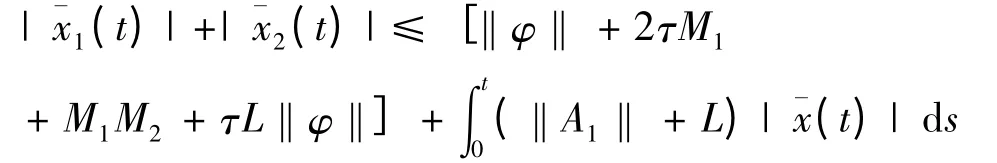
其中:

由引理2.3 Gromwell 不等式得:

又因为(3)和(6)同解则:

即系统(3)的解可指数估计.

证毕.

4 中立型的研究

对于非线性中立型退化时滞微分方程:

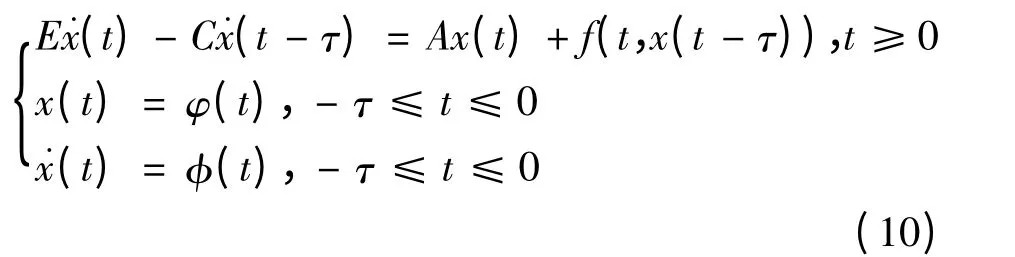
令:

则对(10)系统第一个方程整理得:

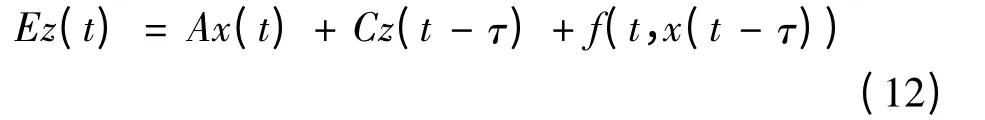
联立方程(11)和(12)得:

设:

则(10)可以化为:

则(10)和(13)同解的，且将非线性中立型退化时滞微分方程转化为一般的非线性退化时滞微分方程研究，其也有解的存在性和指数估计.

具体例子:考虑如下系统:

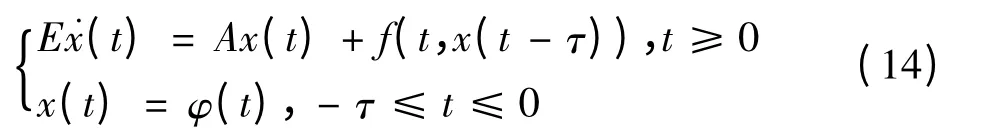
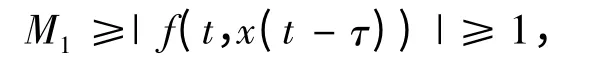
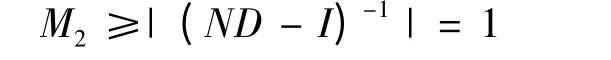
所以有:a=5，b=2

则系统(14)的解满足:

［1］ Mao X.Exponential Stability of Nonlinear Differential Delay Equations［J］.Systems and Control Letters，1996，(28):159－165.

［2］ Jie Chen.On Computing the Maximal Delay Intervals for Stability of Linear Delay Systems［J］.IEEE Transactions on Automatic Control，1995，(40):1087－1093.

［3］ John Chiasson.A Method for Computing the Interval of Delay Values for Which a Differential－delay System is Stable［J］.IEEE Transactions on Automatic Control，1988(33):1176－1178.

［4］ Brierley S D，Chiasson J N，Zak S H.On Stability Independent of Delay for Linear Systems［J］.IEEE Transactions on Automatic Control，1982，(27):252－254.

［5］ 蒋威.时变退化时滞微分系统的变易公式［J］.数学年刊，2003，24A(2):161－166.

［6］ 王晓佳.广义时滞微分方程的渐近稳定性和数值分析［J］.数学理论与应用，2008，28(4):13－16.

［7］ 周先锋.关于退化多时滞泛函微分方程解的研究［J］.应用数学，2009，22(1):177－184.

［8］ 王晓佳.退化时滞中立型微分系统解的存在唯一性及指数估计［J］.应用数学，2011，24(2):384－390.

［9］ Gnatcatcher FR.The Theory of Matrices，Vol.2［M］.New York:Chalse，1974.

［10］ 郑祖庥.泛函微分方程理论［M］.合肥:安徽教育出版社，1994.

［11］ 蒋威.退化时滞微分系统［M］.合肥:安徽大学出版社，1998.

［12］ Dai L.Singular Control Systems［M］.New York:Springer，1989.

［13］ Campbell S L.Singular Systems of Differential Equations［M］.San Francisco:Pitman Advanced Publishing Program，1980.

［14］ 杨冬梅，等.广义系统［M］.北京:科学出版社，2004.

［15］ 苏晓明，等.广义周期时变系统［M］.北京:科学出版社，2006.

［16］ 秦元勋，等.带有时滞的动力系统的稳定性(第2 版)［M］.北京:科学出版社，1989.