关于岭估计改进的研究①
周一美,张 拓
(渤海大学 数理学院,辽宁 锦州121013)
0 引 言
岭估计[1~2]在有偏估计[3]中占有着重要地位,具有很多良好性质,也是很多学者心中最理想的一种有偏估计.目前已有大量学者对其进行了不同程度的改进[4~5],以期获得更小均方误差,以便于解决生产生活中的实际问题.而大部分已经提出的改进后的岭估计都是在线性模型下完成的.一般来讲,对模型的限制条件越少越好,这样会有更广泛的应用价值.
1 广义岭估计的进一步改进
在奇异线性模型中:

现讨论其参数β,σ2估计问题.假设存在Σ >0,则存在唯一正定对称阵使.对其进行如下变换:

则可得到一般线性模型形式:
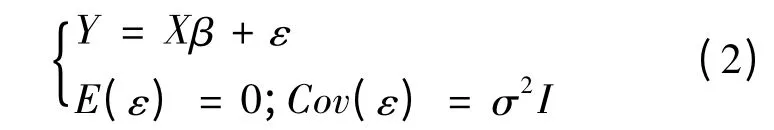
于是可以得到β 的LS 解为:

称其为广义LS 解.线性函数c′β 的可估计性与协方差无关,则对模型(1)的c′β 可估计的充要条件是c ∈μ(X′),称c′^β 为c′β 的广义LS 估计.
模型(2)的典则形式:设X′X=X′Σ-1X 的特征值为λ1,λ2,…,λp,对应的标准正交化特征向量为φ1,φ2,…,φp,记Φ=(φ1,φ2,…,φp),Φ 为p×p 标准正交阵,即Φ′Φ =I.记Δ =diag(λ1,λ2,…,λp),则,其中Z=XΦ,α=Φ′β.
因为,故有:

于是其广义岭估计为:

现对其进行进一步改进,给出β 的一个新估计:

证明:

证毕.
证明:


证毕.
性质3 对任意ki>d >0,有
证明: 对实对称阵X′Σ-1X 进行分解,设rk(X′Σ-1X)=r ≤p,则存在p×p 阶正交阵Q,使:

其中Δr=diag(λ1,λ2,…,λr)为X′Σ-1X 非零特征值组成的对角阵,根据Moore-Penrose 广义逆,^β(K,d)的估计可定义为:


定理得证.
表明当ki>d >0 时是的压缩估计.
定理3.1 存在ki>0,使
证明: 因为:

记


且

故有:

若

则有:

定理得证.
[1] HOERL A.E.,KENNARDR.W..Ridge Regression:Biased Estimation for Non -orthogonal Problems[J].Technometrics,1970,12(1):55-67.
[2] HOERLA.E.,KENNARDR.W..Ridge Regression:Applications to Non-orthogonal Problems[J].Technometrics,1970,12(1):69-82.
[3] 陈希孺,王松桂.近代回归分析-原理方法及应用[M].合肥:安徽教育出版社,1986:217-279.
[4] 张建军,吴晓平.线性回归模型系数岭估计的改进研究[J].海军工程大学学报,2005,17(1):54-57.
[5] 张拓,李胜起,徐坤哲.广义岭型主成分估计优良性研究[J].佳木斯大学学报(自然科学版),32,2014:939-940.

