含可调度分布式电源的配电网综合优化

王 威 黄大为

含可调度分布式电源的配电网综合优化

王 威1,2黄大为3

（1. 山东科技大学机电工程系 泰安市 271019
2. 电网智能化调度与控制教育部重点实验室(山东大学) 济南市 250061 3. 东北电力大学电气工程学院 吉林市 132012）

主动配电网中将分布式电源作为可控可调度机组参与最优潮流运行调度，而现有的方法很难协调优化计算的精度和效率，为此提出一种适合大规模配网、具有较高计算精度的含可调度分布式电源优化算法，即通过优化少环网的连枝上串联理想电压源和网络的近似等效变换，在满足配网辐射状约束的条件下，实现了重构、电容器优化投切和可调度分布式电源出力三者的同时高效优化。算例结果验证了算法的准确性、快速性和对大规模配网的适应性。

配电网 可调度分布式电源 协调优化 理想电压源

1 引言

随着智能化配电网建设的发展，分布式电源（DG, Distributed Generators）大规模渗透到配网[1,2]，会对现有配电网造成广泛的影响，例如潮流方向的改变，线损的改变，增加短路容量，影响供电可靠性和加剧电能质量恶化等。因此，研究含分布式电源的配电网优化问题，可有效降低损耗，提高供电可靠性，具有重要的实际意义。

传统的配电网优化运行问题的主要控制手段是电容器优化投切和网络重构[3-9]，已经取得的大量的研究成果，但随着DG接入配电网和主动配电网技术的发展，问题就转化为含DG的配电网优化问题。DG按调度方式可分为可调度和不可调度两种，可调度DG包括燃气汽轮机、异步电动机等，不可调度DG包括风机和光伏发电，本文聚焦于研究含可调度DG的配电网优化。文献[10,11]提出基于最优潮流算法的配电网主动管理模型，确定可调度DG、需求侧管理、可控负载和无功补偿控制选项的最优组合，但是在控制过程中没有结合重构手段。文献[12]在文献[10]基础上穷举所有可能的网络结构，对每个网络结构再进行优化，在 DG优化过程中考虑了重构手段，但没有将重构作为一种优化手段结合到优化过程中。文献[13]利用奔德斯分解方法实现重构与分布式电源出力、电容器投切组数优化手段交替求解，将重构作为一种优化手段结合到DG优化过程中，但没有实现DG和重构的同时优化。文献[14]采用蚁群算法实现了重构与可调度DG的同时优化，但由于需要满足配电网辐射状约束条件，该算法对大规模配网很难保证计算效率。

为此，本文通过串联理想电压源和基于启发式方法的近似网络等效变换的应用，探索实现重构、电容器优化投切和可调度DG输出三种控制手段的同时高效优化。

2 数学模型

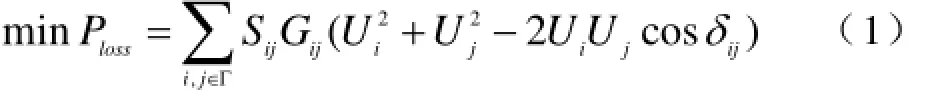
含可调度分布式电源配电网优化目标函数:

式中，Γ为支路集合；Sij为支路i-j上开关的状态，是0-1离散变量，0表示断开，1表示闭合；Gij是支路i-j的电导；Ui,Uj为节点i,j电压幅值；δij为节点i,j之间电压的相角差。

潮流方程等式约束，对于节点i,i=1,2,...n，n为节点个数，约束条件是:

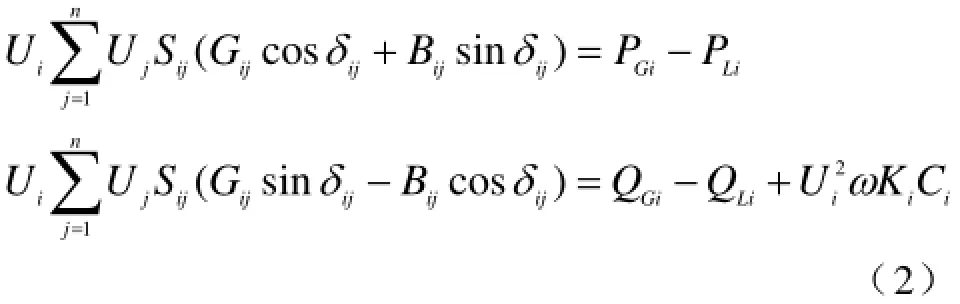
式中，Bij是支路i-j的电纳；PGi,QGi分别是节点i的分布式电源注入有功、无功功率；PLi,QLi分别是节点i的负荷有功、无功功率；ω是角频率；Ki是节点i上并联电容器投入组数；Ci是节点i上并联电容器单组电纳。

不等式约束是:

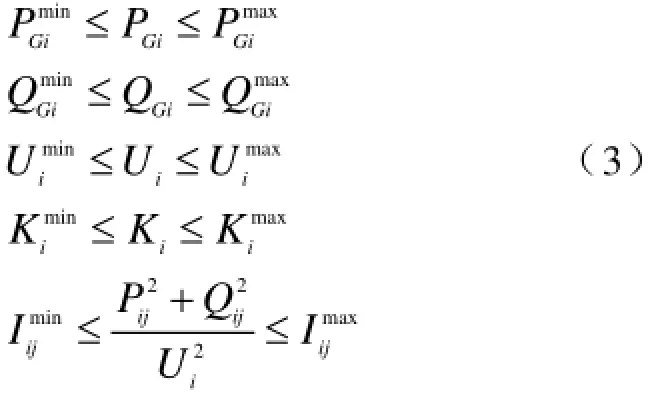
辐射状约束条件是:

式中，x是开关状态组合；D是构成辐射网的开关状态组合集合。

以上模型是一个混合整数非线性规划问题，且满足辐射状约束条件。难点是如何处理重构后必须满足的辐射状约束条件，进而实现三者的同时优化。

3 利用理想电压源的少环网优化方法

3.1含理想电压源的优化模型

上一小节的模型很难采用解析优化方法求解，需将该问题转化为连续变量的优化问题。

若在少环网每一个连支串联一个如图1所示的理想电压源，优化该电压源可以使少环网功率分布达到或接近按支路电阻的反比分布的效果，这与网络重构效果相同。

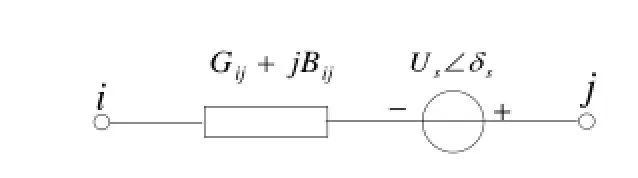
图1 含理想电压源的支路Fig.1 Branch with ideal voltage source

电容器优化投切采用文献[15]方法，在目标函数中引入罚函数，使得电容器投切组数最优解尽可能地逼近离散值，而DG输出本身就是连续量，这样对少环网的优化，就从混合整数规划问题就转化为非线性连续变量优化问题。

少环网连枝上加入理想电压源并引入罚函数后，式（1）修改为:

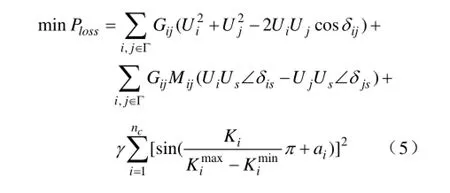
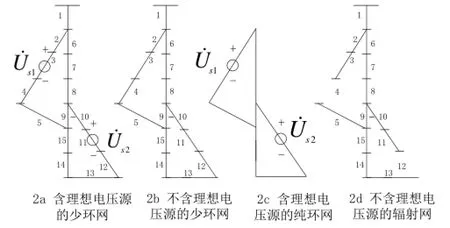
图2 少环网的等效变换Fig.2 Equivalent transform of weakly meshed network

式中，Us为理想电压源的电压幅值；δis,δjs分别是节点i,j电压与理想电压源之间的相角差；由于每个基本回路只有一个串联的理想电压源，若支路i-j上有理想电压源Mij=1，否则Mij=0；nc为电容器个数；这里Ki为连续变量；γ是给定的参数，为了兼顾取整和获得最优解，通常从小到大取值。

式（5）右边第1部分是没有理想电压源支路的损耗，第2部分是有理想电压源支路的网损，第3部分是将电容器投切组数归整的罚函数。

式（5）中的ai的计算公式如下:

潮流方程的约束条件为:

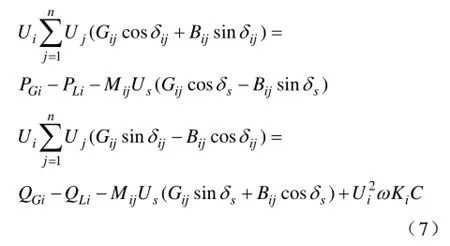
式中，ciX是电容器节点i补偿的电抗值。

不等式约束条件仍为式（3）。

相对于第2小节优化模型，由于是少环网的优化，不考虑式（4）的辐射状约束条件。

以上少环网优化的数学模型属于连续变量的非线性规划，可采用基于原始-对偶内点法的开源优化程序包IPOPT[16]求解。但是，实际配电网辐射状运行且不含理想电压源，下面的问题是如何通过等效变换，将以上模型优化结果转换为不含理想电压源的辐射网，同时使电流分布与以上模型优化结果最接近。

3.2近似的网络变换方法

如图2所示，网络的近似等效变换的目的就是将图2a的网络变换为图2d的网络，同时使二者的支路电流分布最接近。

对于图2a的少环网，分离出含理想电压源的纯环网，可得如图2b和2c两个网络，即图2b的含分布式电源、负荷和电容器的网络，图2c的只含电压源的网络。

对于图2b，若分布式电源出力、负荷值和电容器投切组数与图2a相同，由于去掉理想电压源，潮流分布一定与图2a不同，若断开支路4和12，使图2b转化为图2d的辐射网，同时满足潮流分布与图2a相同，就解决了从含理想电压源的少环网等效变换为不含理想电压源的辐射网的等效变换问题。

考虑到实际电网中，很难对分解出的不含理想电压源的网络每个基本回路中找到一条支路，达到断开后的支路电流与含理想电压源的少环网相同。为此，采用每次断开一条环网支路的启发式方法，重复该过程，直到形成辐射网为止。断开一条支路的启发式方法如下:对于图2b每次断开一条支路，潮流计算断开该支路后形成的辐射支路与图2a相同标号支路电流差的绝对值之和，对所有环网支路都断开一遍，取绝对值之和最小的支路断开。

3.3算法总体流程

根据以上分析，图3给出了算法的总体流程:

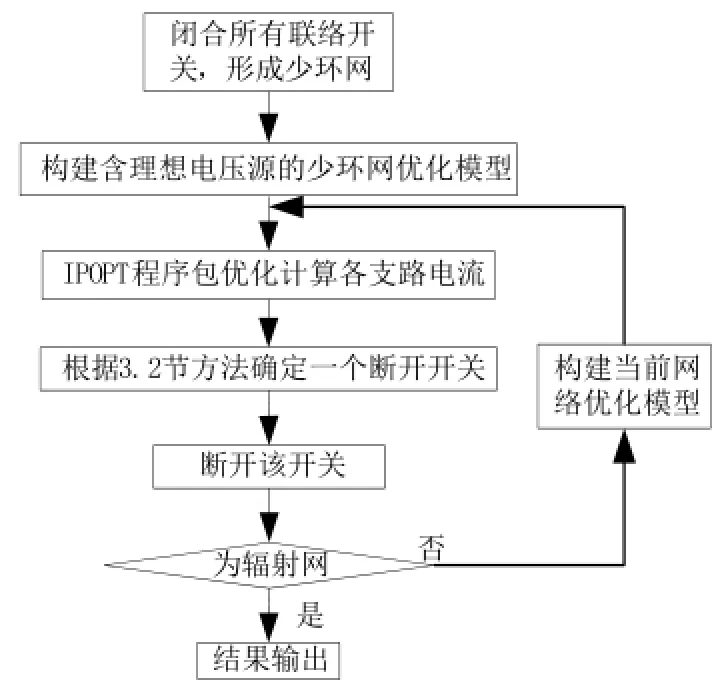
图3 算法流程图Fig.3 Flow chart of algorithm

算法利用优化理想电压源近似代替重构手段，并通过网络近似等效变换间接实现了重构、DG输出和电容器优化投切的同时优化，提高了计算精度。算法的计算量为与环网次数个数的优化计算次数和与开关个数接近的潮流计算次数，计算效率高，适合大规模配电网优化计算。

4 算例及分析

4.1IEEE69节点算例

本文的算法在IPOPT程序包基础上用C++语言编程，在Intel Pentium（D）CPU 2.80MHz计算机实现，以如图4所示的IEEE 69节点[17]为算例，基准容量是100MVA，基准电压12.66KV，节点19、47和52是电容器节点，在节点38、50分别增加2台可调度式分布式电源，分布式电源参数如表1所示。

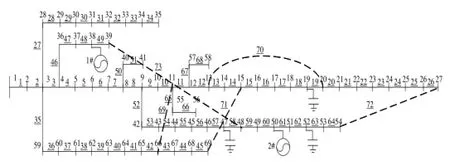
图4 含可调度分布式电源IEEE 69节点系统Fig.4 IEEE 69 systems with dispatched DG

表1 分布式电源参数Tab.1 Parameter of DG

表2给出了算例的迭代过程。

表2 迭代过程表Tab.2 Process of iteration

表3给出了本文优化结果与电容器投切、分布式电源优化与重构交替迭代的求解方法比较，其中重构采用文献[18]的方法，电容器优化投切和可调度分布式电源优化采用文献[16]的方法。

表3 结果比较表Tab.3 Comparison of results

由表3可知，本文方法相对于交替迭代方法降低了网损，提高了计算效率。

4.2实际大规模配网算例

为了验证算法对大规模配电网的快速计算能力， 本文对某城市的不同规模配网加入分布式电源后的网络验证计算，结果如表4所示。

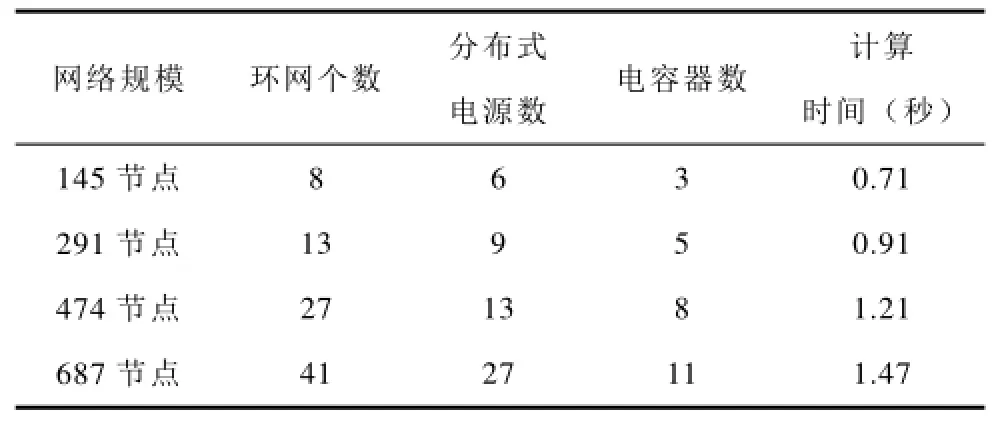
表4 不同配网优化时间表Tab.4 Computation times of different distribution networks

由上表可知，随着网络规模的增加，算法计算时间增加较小，算法具有很高的计算效率。

5 结论

通过优化引入的理想电压源和网络近似等效变换，将考虑辐射状约束的混合整数规划转化连续变量的优化和潮流问题求解，具有一定的理论意义。间接的实现了重构、可调度DG输出和电容器投切优化的同时高效优化，提高了优化精度。数值分析结果表明相对于交替迭代优化，提高了优化精度，适合大规模配电网优化。

[1] 尤毅, 刘东, 于文鹏等. 主动配电网技术及其进展[J]. 电力系统自动化, 2012, 36(18): 10-16.

You Yi, Liu Dong, Yu Wenpeng, et al. Technology and its trends of active distribution network[J]. Automation of Electric Power Systems, 2012, 36(18): 10-16.

[2] Samuelsson O, Repo S, Jessler R, et al. Activedistribution network-demonstration projection ADINE [C]. Proceeding of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe, October 11-13, 2010, Gothenburg, Sweden: 8p.

[3] Su C T, Lee C S. Feeder reconfiguration and capacitor setting for loss reduction of distribution systems[J]. Electric Power Systems Research, 2001, 58: 97-102.

[4] 刘莉, 宛力, 陈学允. 模糊遗传算法在配电网络综合优化中的应用[J]. 电力自动化设备, 2001, 21(1): 14-16.

Liu Li, Wan Li, Chen Xueyun. Application of fuzzy genetic algorithm to optimal coordination of distribution network[J]. Electric Power Automation Equipment, 2001, 21(1): 14-16.

[5] 许立雄, 吕林, 刘俊勇. 基于PSO的配网重构与电容器投切综合优化算法[J]. 继电器, 2006, 34(17): 25-28.

Xu Lixiong, Lu Lin, Liu Junyong. Comprehensive optimization of distribution network reconfiguration and capacitor switching based on particle swarm optimization[J]. RELAY, 2006, 34(17): 25-28.

[6] 邓佑满, 张伯明, 王洪璞. 配电网络重构和电容器投切的综合优化算法[J]. 电力系统自动化, 1996, 20(5): 5-9.

Deng Youman, Zhang Boming, Wang Hongpu. A comprehensive optimization algorithm for distribution network reconfiguration and capacitor switching [J]. Automation of Electric Power Systems,. 1996, 20(5): 5-9.

[7] Zhang D, Fu Z C, Zhang L C. Joint optimization for power loss reduction in distribution systems[J]. IEEE Trans. Power Systems, 2008, 23(1): 161-169.

[8] Jiang D, Baldick B. Optimal electric distribution system switch reconfiguration and capacitor control [J]. IEEE Trans. Power Systems, 1996, 11(2): 890-897.

[9] 王威, 韩学山, 王勇等. 配电网重构及电容器投切综合优化方法[J]. 电网技术, 2010, 34(12): 90-93.

Wang Wei, Han Xueshan, Wang Yong, et al. A Compositive Optimization Algorithm for Distribution Network Reconfiguration and Capacitor Switching[J]. Power System Technology, 2010, 34(12): 90-93.

[10] PILO F, PISANO G, SOMA G G.. Advanced DMS to manage active distribution network[C]. Proceeding of the 2009 IEEE Bucharest PowerTech Conference, June 28-July 3, 2009, Bucharest, Romania: 8p.

[11] A. Broghetti, M. Bosetti, S. Grillo, et al. Short-term scheduling and control of active distribution systems with high penetration of renewable resources[J]. IEEE Systems Journal, Special Issue on “Identification and Control of Sustainable Energy Systems”, 2010, 4(3): 313-322.

[12] PILO F, PISANO G, SOMA G. Optimal coordination of energy resources with a two-stage online active management[J]. IEEE Trans on Industrial electronics, 2011, 58(10): 4526-4537.

[13] H. M. Khodr, J. Martinez-Crespo, M. A. Magos, et al. Distribution systems reconfiguration based on OPF using Benders decomposition power[J]. IEEE Trans. Power Del, 2009, 24(4): 2166-2176.

[14] Y. -K. Wu, C. -Y. Lee, L. -C. Liu et al. Study of reconfiguration for the distribution system with distributed generators[J]. IEEE Trans. Power Del, 2010, 25(3): 167-1685.

[15] E. M. Soler, E. N. Asada. Penalty-based nonlinear solver for optimal reactive power dispatch with discrete controls[J]. IEEE Trans on Power Systems, 2013, 28(3): 2174-2182.

[16] Wächter Andreas, Biegler Lorenz T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming[J]. Mathematical Programming, 2006, 106(1): 25-57.

[17] Su C T, Lee C S. Feeder reconfiguration and capacitor setting for loss reduction of distribution systems[J]. Electric Power Systems Research, 2001, 58: 97-102.

[18] 王威, 韩学山, 王勇, 等. 一种减少生成树数量的配电网最优重构算法[J]. 中国电机工程学报, 2008, 28(16): 34-38.

Wang Wei, Han Xueshan, Wang Yong, et al. A distribution network optimal reconfiguration algorithm of reducing the number of spinning trees[J]. Proceedings of the CSEE, 2008, 28(16): 34-38.

The Coordination Optimization of Distribution Networks with Dispatched Distributed Generators

The distributed generators(DGs) are regarded as the dispatched generators participating in Optimal Power Flow(OPF) in active distribution networks. But the conventional algorithms could not coordinate the precision and efficiency. This paper proposes an efficient and high calculation precision joint optimal algorithm with dispatched DGs. The proposed algorithm implements the reconfiguration, capacitor switching and output of the dispatched DG joint optimization by the optimization of imaginary ideal voltage sources that in series with link branch and approximate equivalent conversion of networks. At the same time the radial constrains are satisfied. The different size of test systems were performed showing the efficiency and precision of the proposed algorithm.

Distribution systems; dispatched DG; coordination optimization; ideal voltage sources

TM315

王威 男，1974年生，博士后，讲师，主要从事配电网络优化理论方面的研究。

电网智能化调度与控制教育部重点实验室2012年度开放基金(2012A-02)；青岛市博士后研究人员应用研究项目资助基金；甘肃省教育厅科研项目(1115-03)。

2014-09-10

Wang Wei1,2 Huang Dawei3

（1. School of Machine and Electric Engineering Shandong Science and Technology University Taian 271019 Shandong Province China 2. Key Laboratory of Power System Intelligent Dispatch and Control (Shandong University) Ministry of Education Jinan 250061 China 3. Scholl of Electrical Engineering, Northeast Dianli University JiLin 132012 China）

黄大为 男，1976年生，博士，副教授，主要从事电力系统运行与控制的研究。