基于类别语言值的电能质量信号模糊分类

刘晓胜 刘 博 徐殿国

基于类别语言值的电能质量信号模糊分类

刘晓胜 刘 博 徐殿国

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

模糊逻辑方法已被广泛用于电能质量信号的分类，但在模糊分类系统设计过程中存在过多的不确定因素，增加了设计过程的复杂性，不易得到好的分类结果。针对这一问题，本文提出一种基于类别语言值的电能质量信号模糊分类方法。该方法直接用待分类的各个类别来定义模糊输入变量的语言值，根据各个类别对应的输入变量取值来设定隶属函数。所设计分类系统的模糊规则直接来自于对输入量数值分布的分析，规则数量与类别数量相同。输入模糊变量的语言值和隶属函数的设计，不再只与输入量相关，而且与待分类信号性质、分类结果直接相关。仿真和实测数据的分类识别结果表明了这种模糊分类方法的可行性和有效性。

电能质量 模糊逻辑 类别语言值 特征选择

1 引言

现代电力系统中，电力电子设备的应用越来越广泛，各种非线性、冲击性、波动性负载大量增加，使电力系统所遭受的电能质量扰动日趋严重。随着电网规模的不断扩大和用户对电能质量要求的不断提高，如何提高电能质量、保证供电可靠性，受到日益广泛的关注。电能质量信号的分类是评估和改善电能质量的必要前提。

电能质量信号可采用支持向量机[1-3]、二进制特征矩阵[4]、Markov模型等方法进行分类[5]。近年来，由于电能质量信号本身的复杂性和类别的多样性，模糊逻辑[6-9]、神经网络[10-13]等人工智能方法的应用越来越受到关注。模糊分类与神经网络分类同样易于表述电能质量信号包含的非线性信息；但是，模糊逻辑是对人类模糊思维过程的模拟，模糊分类更易于融合、利用人类所具有的相关经验知识，且算法复杂度相对神经网络分类较低，因此成为电能质量信号分类的另一有效方法。文献[9]提出一种采用决策树-模糊（DT-F）规则库的电能质量扰动信号分类器。DT-F规则库的复杂性是限制其应用的一个重要因素。文献[14]采用小波变换对电能质量信号进行特征量提取，并设计了一种基本的模糊分类器实现了分类。但噪声等因素的影响同样会使分类正确率大大降低。文献[15]提出一种基于小波变换的模糊推理方法，但并未通过加入噪声来验证所提方法的鲁棒性。文献[16]同样采用小波变换来提取电能质量信号的特征量，并将神经网络和模糊逻辑相结合进行信号分类。文献[17]对电能质量信号进行广义S变换，获取5个特征值用于分类。为降低系统复杂度，对模糊规则库进行了精简，设计了12条规则。显然，为使这样的规则精简有效，必然要求模糊推理过程的其他部分与规则密切配合，尤其是输入模糊变量的语言值个数、隶属函数形状及位置参数。然而，在传统的模糊推理方法中，这些参数和模糊规则的设计都是相互独立的。虽然模糊分类系统的各个组成部分相互联系，对分类结果都有重要影响，但是各个部分的设计过程并没有体现出这种内在的联系。如输入模糊变量的语言值个数、隶属函数参数的设计，只与输入变量的取值相关，而与分类目的之间没有直接联系。于是，在模糊分类系统的设计过程中，出现了过多的不确定因素，增加了设计过程的复杂性，不易得到好的分类结果。本文针对这一问题，探求改进模糊推理方法，简化设计过程。这样的尝试有可能使电能质量信号模糊分类面临的问题得到更好地解决。

本文提出了类别语言值模糊分类方法，并用来解决9类电能质量信号的分类问题。第二部分论述了类别语言值模糊分类方法，给出了基于该方法的模糊分类系统设计过程。第三部分针对电能质量信号的分类问题，设计了类别语言值模糊分类系统，并进行了验证。结果表明，分类计算量较小，分类正确率较高。

2 类别语言值模糊分类方法的提出

在模糊逻辑中，输入输出变量选择、设定语言值、定义隶属函数、模糊推理方法设计、解模糊方法设计等环节，对模糊推理的结果都有影响。隶属函数是用来在模糊逻辑与精确的现实数据之间建立起联系的纽带，也是最为重要的模糊运算环节，对模糊推理的最终结果有重要影响。

隶属函数总是与模糊变量的取值（语言值）一一对应，模糊变量的每一个取值都有一个定义在论域上的隶属函数与之对应。模糊变量的取值与该模糊变量输入具体数值的大小相关；为便于表述，通常记为正大（PB）、正小（PS）、零（ZO）、负小（NS）、负大（NB）等。如果需要做更细致的论域划分，则增加正中（PM）、负中（NM）之类的语言值。基于上述隶属函数设置，模糊推理规则的数量与输入模糊变量的语言值数量（亦即隶属函数数量）直接相关。如对于二输入单输出的模糊推理系统，若2个输入模糊变量各有5个语言值，则其完整的模糊规则数为5×5=25条。

利用模糊逻辑构造模糊推理系统对电能质量信号进行分类，其输入模糊变量的数量通常大于2个，于是完整的模糊规则数量也较多。考虑到在线实现的实时性，以及必要性，通常在电能质量信号分类模糊系统设计中，需要设计适当的原则，对规则进行取舍，以减少规则数量，从而减少计算量，加快响应速度。而规则的取舍，不论设计怎样的取舍原则，对具体问题总会出现两难的境地。其结果或者是保留了太多规则而增加了计算复杂度并可能导致过拟合，或者是因为舍去了一些规则而导致识别正确率下降。

从另一个方面来看，上述输入模糊变量语言值及其隶属函数的设计方法，仅与输入模糊变量的性质相关。这种方法对于需要输出精确数值以便作用于现实对象的一般模糊推理系统是合适的，但是，对于模糊分类系统就不一定是最合适的了。模糊分类系统是用来对输入对象进行分类的模糊推理系统，它的目的是分类，它需要得到的是离散的分类结果，而不是精确的、连续变化的输出数值。由此，若能在输入模糊变量语言值及其隶属函数的设计中，不只考虑输入变量的性质和特征，同时考虑推理系统输出端的分类要求，则有可能得到更适合于分类应用场合的新的模糊推理系统设计方法。

为便于电能质量信号的模糊分类，通常需要采用适当的数学变换，将测得的电能质量信号数据序列变换为几个特征量，然后基于这几个特征量进行模糊分类。对模糊分类系统来说，这些特征量就是系统的输入变量，系统的输出则是分类的结果，即电能质量信号的类别，如电压暂升、电压暂降、电压中断、切口、谐波等。

针对电能质量信号分类这一问题，考虑电能质量信号模糊分类器简化模糊规则的需要与传统模糊推理机制之间的差异，本文提出以下设想:在输入模糊变量的论域上，直接以电能质量信号的类别（如电压暂升、电压暂降等）作为语言值，并根据输入变量的特性来定义与之对应的隶属函数。如上所述，输入模糊变量为用来表征电能质量信号扰动信息的特征值。对于每个电能质量信号类别来说，每个特征值都会有一个与之对应的取值范围，隶属函数需要涵盖这个范围，并具有合适的函数表达式，即具有合适的延展性。

综上所述，由于输入模糊变量取值直接与输出的分类结果一一对应，模糊规则数即等于分类数，规则数量显著降低。这种设想，本文称之为类别语言值模糊分类方法。

3 电能质量信号的类别语言值模糊分类

为实现电能质量信号的分类识别，首先需要对电能质量信号进行适当的数学变换，以利于提取能够表征信号本质特性的特征量；再以这些特征量为输入变量，与类别语言值模糊分类方法结合进行信号分类。

3.1特征量选取

基于数学变换的特征提取，是电能质量信号分类的基础。S变换是一种可逆的局部时频分析方法，其高斯窗口随频率变化，具有更高、分布通常更合理的频率分辨率，并可以独立分析信号各频率分量的幅值变化[18]，是一种相对较好的变换方法，有利于提取多样的电能质量信号特征值。窗宽可调整的广义S变换则使特征值提取具有了更大的自由度。信号h(t)的广义S变换离散计算式为

式中，H(n+i)是h(n+i)的傅里叶变换；k为窗宽调整系数，且k＞0；N为总采样点数；m=0，1，2，…，N-1；n=0，1，2，…，(N-1)/2。

根据IEEE相关标准，给出9种待分类电能质量信号的数学模型，如表1所示。其中标准信号的基础频率为50Hz，电压幅值为归一化值，u(t)为单位阶跃函数。设定采样频率为录波器常用的3 200Hz，连续采样点数1 024点，使用上述模型，计算得到电能质量信号采样时间序列的样本数据。为尽量保证数据样本对实际中可能出现的信号的全覆盖，每种信号在其模型参数允许变化范围内随机产生98个样本，再添加信号模型参数取最大值和最小值的情况，共得到98+2=100个样本，上述9种信号共得到900个数据样本。对每个样本，添加噪声，作广义S变换，得到S变换结果矩阵S(i，j)。S变换结果矩阵（简称S矩阵）的行数为M=513，列数N=1 024。

表1 标准信号及电能质量扰动信号仿真模型Tab.1 Simulation models of power quality signals

基于S矩阵，设定用来作为分类依据的电能质量信号特征量如下。

（1）特征量F1。S矩阵幅值-时间数据在基频附近的均值。计算式为

以电网基础频率50Hz为例。因为数据采样频率为3 200Hz，故S矩阵相邻两行之间的频率差为3.125Hz。所以将基本频率附近取为S矩阵的第15～19行。

（2）特征量F2。S矩阵幅值-时间数据在基频附近的幅值标准差。计算式为

（3）特征量F3。S矩阵的谐波含量。分母为无扰动标准正弦信号的S矩阵基频附近数值的平方和开根号，记为V。分子则为其他所有频率点数值的平方和开根号。于是，可得F3的计算式为

（4）特征量F4。计算与F3类似，是800Hz以上的谐波数值平方和开根号与无扰动标准正弦信号的S矩阵基波附近数值的平方和开根号值之比。该特征量专用于区分振荡信号。计算式为

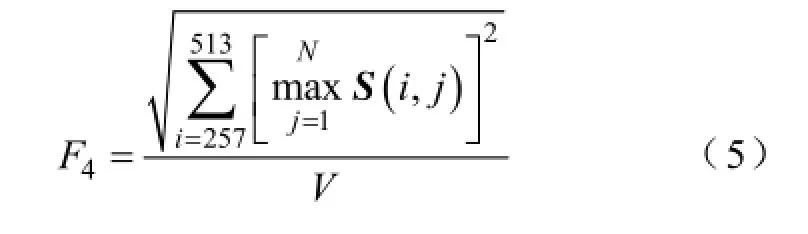
本文选取上述4个特征量来区分9类电能质量信号。在相同或相近的分类数条件下，本文特征量个数明显少于多数国内外同类研究文献。而特征量数目少，通常表明所设计的分类器结构简单、计算量少。

对上述所有样本数据，作广义S变换，得到S矩阵，分别按照式（2）～式（5）计算特征量F1、F2、F3、F4的数值。计算出全部样本的特征值，即可确定各个特征量（即模糊分类推理系统的输入量）的论域。进而根据样本特征量数值的分布情况，可在论域上定义对应于各个类别语言值的隶属函数。同时，根据样本特征量数值的分布情况，还可分析确定，依据这些特征量是否能够区分9类电能质量信号。若存在不能区分的信号，则应考虑增、减或更换特征量。需要指出的是，本文给出的4个特征量就是通过上述过程确定的。

3.2论域及隶属函数确定

具体来说，各类信号所有样本的特征量计算值的分布范围即为该特征量的论域，而每类信号的特征值分布范围即为该类信号（模糊输入变量的语言值）隶属函数的大致分布范围。下面以特征量F1为例进行说明。

F1是所设计模糊分类推理系统的一个输入量，其语言值直接取为待分类的信号类别，即标准、电压暂降、电压暂升、电压中断、谐波、电压闪变、振荡、尖峰、切口等9个语言值，依次记为F1Normal、F1Sag、F1Swell、F1Interruption、F1Harmonics、F1Flicker、F1Transients、F1Spike、F1Notch。

取隶属函数为改进的高斯型函数，即

式（6）中，a、b、σ为隶属函数形状参数，计算式为

式中，F1min、F1max分别为该类信号F1值的最小值、最大值。这样计算出的隶属函数参数，使高斯隶属函数中间隶属度为1的区域覆盖F1min至F1max区域的80%，F1=F1max或F1min时的隶属度都约为0.75。

上述900个样本的特征量F1计算结果如图1所示，图中横坐标为特征量F1的计算值。为将9类信号各自的特征值F1在图中区分开来，图1的纵坐标对各类信号分别设定为不同的固定值，图中由下至上依次为标准、电压暂降、电压暂升、电压中断、谐波、电压闪变、振荡、尖峰、切口9类信号的特征值，其纵坐标具体数值没有实际意义。

图1 特征量F1的样本计算值Fig.1 Samples of F1

图1 中，所有样本特征量F1计算值的变化范围为[5.40489E-4，1.90017]，对该变化范围的最小值作向下取整，对最大值进行向上取整运算，将其论域设定为[0，2]。如上所述，定义在论域上的语言值有9个，分别对应于9类信号的F1值。根据每类信号特征值数值的最大、最小值，由式（7）可以确定相应语言值的隶属函数参数，从而得到该语言值的隶属函数。电压暂降信号的特征值（对应于图1中纵坐标值为1的数据点）的最大、最小值分别为0.900 27、0.099 71，代入式（7），可计算出语言值F1Sag的隶属函数参数a=0.179 766、b=0.820 214和σ=0.152 106 4。依此类推，可确定模糊输入变量F1的所有9个语言值的隶属函数，如图2所示。图2中，标出了3个隶属函数对应的语言值；其他隶属函数几乎重叠在一起，不便标出语言值。

图2 特征量F1的语言值与隶属函数Fig.2 Linguistic values and membership functions of F1

以此类推，可以确定其他3个模糊输入变量F2、F3和F4的各个语言值的隶属函数。图3、图4分别给出了特征量F2、F3的样本计算结果，与之对应的语言值隶属函数分布情况分别如图5、图6所示，其分布同样遵循每类信号特征值的样本数据计算结果，但与图2所示F1隶属函数的分布情况有很大差别，反映了电能质量信号特征的不同侧面。

图3 特征量F2的样本计算值Fig.3 Samples of F2

图4 特征量F3的样本计算值Fig.4 Samples of F3

图5 特征量F2的语言值与隶属函数Fig.5 Linguistic values and membership functions of F2

图6 特征量F3的语言值与隶属函数Fig.6 Linguistic values and membership functions of F3

3.3模糊规则提取

观察图1可以发现，电压暂降、电压暂升、电压中断3类信号的F1数值与其他6类信号有明显差异，这三类信号仅依据F1值就可以进行分类识别。而其他6类信号的F1数值都分布在1附近的狭小区域，其分类识别需要借助其他特征量。

如上所述，特征量F4专用于识别振荡信号。在电压暂降、电压暂升、电压中断和振荡4类信号可识别的情况下，下面分析如何识别其他5类信号。观察图3所示特征量F2的样本计算值，电压闪变信号的取值与其他4类信号互不重叠，故可利用特征量F2识别电压闪变信号。同时可以看出，标准、谐波两类信号的数值，与尖峰、切口两类信号可明显区分，但各自又有重叠，需要借助特征量F3来识别。观察图4，标准和谐波、尖峰和切口两组信号各自取值都有明显区别。于是，这4类信号可由特征量F2、F3的组合来区分。

通过上述分析，得到所有9类信号的分类依据，于是直接得到了如下9条用于分类的模糊规则，每条规则对应于1类信号。

（1）if [(F1 is F1Normal) and (F2 is F2Normal) and (F3 is F3Normal)] then Signal is Normal

（2）if (F1 is F1Sag) then Signal is Sag

（3）if (F1 is F1Swell) then Signal is Swell

（4）if (F1 is F1Interruption) then Signal is Interruption

（5）if [(F1 is F1Harmonics) and (F2 is F2 Harmonics) and (F3 is F3Harmonics) and (F4 is not F4Harmonics)] then Signal is Harmonics

（6）if [(F1 is F1Flicker) and (F2 is F2Flicker) and (F3 is F3Flicker)] then Signal is Flicker

（7）if [(F1 is F1Transients) and (F2 is F2 Transients) and (F3 is F3Transients) and (F4 is F4Transients)] then Signal is Transients

（8）if [(F2 is F2Spike) and (F3 is F3Spike) and (F4 is F4Spike)] then Signal is Spike

（9）if [(F2 is F2Notch) and (F3 is F3Notch) and (F4 is F4Notch)] then Signal is Notch

上述规则中，规则5中的“not”代表非运算。其中，规则2、3、4对应于电压暂降、电压暂升、电压中断3类信号的识别。如上所述，仅靠F1即可对其进行识别，所以对应规则的前提部分仅有对输入特征量F1的判断。其他6条规则的前提部分相对复杂一些，构成依据如前述。

4 电能质量信号模糊分类结果

4.1仿真结果

上述9条模糊规则的合成采用最大隶属度法，选择所有信号类别中前提满意度最大的一个类别作为分类结果。

为验证所设计分类方法的有效性，采用上述900个样本进行分类识别。为检验所提方法的抗噪能力，产生信号的过程中加入了随机产生的白噪声，样本数据的信噪比为分别为50dB和20dB。分类结果如表2所示。

表2 仿真实验分类结果Tab.2 Classification accuracies of simulation

由表2可见，新方法能够适应不同信噪比条件下的电能质量信号分类要求；在高噪声的情况下，新方法也具有较高的分类正确率，具备良好的抗噪性能，表明了所提方法的可行性和有效性。相较于传统模糊分类方法，新方法结构简单、计算量小。

4.2实测数据校验结果

为进一步验证所提方法在电力系统应用中对实际数据的分类效果，采用国内500kV输电线故障录波数据对电能质量扰动分类进行校验。所用实测电能质量数据由山大电力公司录波设备采集并记录。每类电能质量信号实测数据20组，限于电力系统实测数据数量，部分波形来自实验室可编程序电能质量扰动发生器。采用实测数据进行电能质量信号分类结果如表3所示。

表3 实测数据校验结果Tab.3 Classification accuracies of real data verification

由表3可知，采用所提方法进行实测电能质量信号分类仍然可以得到较高的分类正确率，进一步验证了本文所提方法的有效性。

5 结论

模糊逻辑本质上的模糊特性使得模糊推理方法成为信号分类识别领域的一种常用方法。为保证分类的有效性并降低系统计算复杂度，模糊分类系统的设计需要很多的技巧，无论是语言值个数的选择、隶属函数分布的确定，还是模糊推理规则的设计，都有不小的复杂性。而且这些相对独立的部分，对分类结果都有重要影响，需要反复的试凑，有时还需要借助粒子群算法等智能优化方法。但是优化方法的引入，如果没有与特定分类问题相关的足够的约束条件，又可能影响到模糊分类系统的泛化性能。

本文以9类电能质量信号的分类识别为例，提出了一种新的模糊分类方法。该方法将语言值选择和隶属函数的分布直接与待分类信号性质、分类目的相联系，而不是仅取决于输入量的数值分布。该方法中，各个输入模糊变量的语言值个数与待分类的类别数量相同，隶属函数参数直接由各个类别的相关数据计算得到。模糊规则数量也与类别数量相同，且可直接得到对输入量值分布的分析。

由于将分类的目的融入语言值选择和隶属函数的设计，这种模糊分类方法的设计过程，主要是选择合适的输入模糊变量，其他部分的设计则有了较多的确定性，于是大大减少了设计工作量。并且，模糊规则数量与类别数量相同，减少了模糊分类系统的在线计算量，保证了分类识别的响应速度。

电能质量信号的分类识别结果表明了这种模糊分类方法的有效性。虽然是以电能质量信号分类为例，但这种方法也可以被用于其他分类应用场合。

[1] 黄南天, 徐殿国, 刘晓胜. 基于S变换与SVM的电能质量复合扰动识别[J]. 电工技术学报, 2011, 26(10)： 23-30.

Huang Nantian, Xu Dianguo, Liu Xiaosheng. Identification of power quality complex disturbances based on S-Transform and SVM[J]. Transactions of China Electrotechnical Society, 2011, 26(10)： 23-30.

[2] 李庚银, 王洪磊, 周明. 基于改进小波能熵和支持向量机的短时电能质量扰动识别[J]. 电工技术学报, 2009, 24(04)： 161-167.

Li Gengyin, Wang Honglei, Zhou Ming. Short-time power quality disturbances identification based on improved wavelet energy entropy and SVM[J]. Transactions of China Electrotechnical Society, 2009, 24(04)：161-167.

[3] 秦业, 袁海文, 袁海斌, 等. 基于优化最小二乘支持向量机的电能质量扰动分类[J]. 电工技术学报, 2012, 27(08)： 209-214.

Qin Ye, Yuan Haiwen, Yuan Haibin, et al. Classification of power quality disturbances based on optimized least squares support vector machine[J]. Transactions of China Electrotechnical Society, 2012, 27(08)： 209-214.

[4] 王丽霞, 何正友, 赵静. 一种基于线性时频分布和二进制阈值特征矩阵的电能质量分类方法[J]. 电工技术学报, 2011, 26(04)： 185-191.

Wang Lixia, He Zhengyou, Zhao Jing. Power quality disturbance classification based time-frequency distribu-tion and binary threshold on linear feature matrix [J]. Transactions of China Electrotechnical Society, 2011, 26(04)： 185-191.

[5] Dehghani H, Vahidi B, Naghizadeh R A. Power quality disturbance classification using a statistical and wavelet-based hidden Markov model with dempster-shafer algorithm[J]. Electrical Power and Energy Systems, 2013, 47： 368-377.

[6] Abdelsalam A A, Eldesouky, A A, Sallam A A. Classification of power system disturbances using linear Kalman filter and fuzzy-expert system[J]. International Journal of Electrical Power&Energy Systems. 2012, 43(1)： 688-695.

[7] Rodriguez A, Aguado J A, Martin F. Rule-based classification of power quality disturbances using S-transform[J]. Electric Power Systems Research, 2012, 86： 113-121.

[8] Kapoor R, Gupta R. Fuzzy lattice based technique for classification of power quality disturbances[J]. European Transactions on Electrical Power, 2012, 22(8)： 1053-1064.

[9] Samantaray S R. Decision tree-initialised fuzzy rulebased approach for power quality events classification[J]. IET Generation Transmission & Distribution, 2010, 4(4)： 538-551.

[10] 管春, 周雒维, 卢伟国. 基于多标签RBF神经网络的电能质量复合扰动分类方法[J]. 电工技术学报, 2011, 26(08)： 198-204.

Guan Chun, Zhou Luowei, Lu Weiguo. Recognition of multiple power quality disturbances using multilabel RBF neural networks[J]. Transactions of China Electrotechnical Society, 2011, 26(08)： 198-204.

[11] Mishra S, Bhende C N, Panigrahi B K. Detection and classification of power quality disturbances using s-transform and probabilistic neural network[J]. IEEE Transactions on Power Delivery, 2008, 23(1)： 280-287.

[12] Yap K S, Lim C P, Au M T. Improved GART neural network model for pattern classification and rule extraction with application to power systems[J]. IEEE Transactions on Neural Networks, 2011, 22(12)： 2310 2323.

[13] Lee C Y, Shen Y X. Optimal feature selection for power quality disturbances classification[J]. IEEE Transactions on Power Delivery, 2011, 26(4)： 2342-2351.

[14] Meher S K, Pradhan A K. Fuzzy classifiers for power quality events analysis[J]. Electric Power Systems Research, 2010, 80(1)： 71-76.

[15] Zhu T X, Tso S K, Lo K L. Wavelet-based fuzzy reasoning approach to power quality disturbance recognition[J]. IEEE Transactions on Power Delivery, 2004, 19(4)： 1928-1935.

[16] Reaz M B I, Choong F, Sulaiman M S, et al. Expert system for power quality disturbance classifier[J]. IEEE Transactions on Power Delivery, 2007, 22(3)：1979-1988.

[17] Behera H S, Dashb P K, Biswal B. Power quality time series data mining using S-transform and fuzzy expert system[J]. Applied Soft Computing, 2010, 10： 945-955.

[18] Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum： the S-transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4)： 998-1001.

Fuzzy Classification of Power Quality Signals Based on Pattern Linguistic Values

Liu Xiaosheng Liu Bo Xu Dianguo
（Harbin Institute of Technology Harbin 150001 China）

There are some uncertain factors in the design process of fuzzy system for classification of power quality signals, so that the complexity of the design process is increased and the classification accuracy is usually not very high. To solve these problems, a new fuzzy classification method of power quality signals is proposed in this paper, namely pattern linguistic values method. Patterns of power quality signals to be classified are directly used to define the linguistic values of fuzzy inputs variables in this way, and the membership functions are defined depending on the values of input variables for each pattern. Besides, fuzzy rules are directly obtained from the analysis of distribution of input variable values, and the number of rules is equal to the number of patterns. Thus, the design of linguistic values and membership functions are directly related to the characters of signals to be classified and classification purposes, not just depending on the distribution of input values. Simulation and real data verification results show the validity and efficiency of the proposed method.

Power quality, fuzzy logic, pattern linguistic values, feature selection

TM714.3

刘晓胜 男，1966年生，教授，博士生导师，研究方向为电能质量控制、智能变电站通信、电力线载波通信等。

国家自然科学基金（51277042）资助项目。

2014-05-08 改稿日期 2015-03-16

刘 博 女，1985年生，博士研究生，研究方向为电能质量分析与控制。