一种智能配电网安全运行控制方法
陈 春 汪 沨 刘 蓓 曹一家 刘 玮
一种智能配电网安全运行控制方法
陈 春1汪 沨1刘 蓓2曹一家1刘 玮3
(1. 湖南大学电气与信息工程学院 长沙 410082 2. 江西省电力科学研究院 南昌 330096 3. 广东电网公司 广州 510082)
分布式电源(DGs)高渗透率接入,将改变配电网结构及潮流分布,需要对传统电压与负载率的控制方法进行改进。本文通过分析分布式电源接入后对配电网电压及负载率的影响,提出了一种基于灵敏度分析的多阶段决策的节点电压与线路负载率实时控制方法,有机融合了调节分布式电源出力、调节无功补偿装置、网络重构以及切负荷等控制手段,各阶段根据指标函数值判断是否执行。以改进IEEE 33节点系统作为算例,仿真一天内负荷及分布式电源出力的变化,对于节点电压与线路负载率越过限值时刻给出相应的控制措施,结果验证了本文方法的正确性。
分布式电源 节点电压与线路负载率 多阶段决策 灵敏度分析
1 引言
能源枯竭、能源安全以及环境危机,促使以风电、光伏为代表的可再生能源大规模并网发电趋势不可阻挡[1]。分布式电源作为可再生能源并网发电的重要利用形式,必将逐步实现规模化,高渗透率化[2-3]。
风速以及光照强度皆具有很强的不确定性,加上配电网负荷也具有一定的随机性,使得配电网的潮流分布频繁变化,节点电压幅值以及线路负载率不断改变。线路过载会引起继电保护的误动导致发生停电事故[4],节点电压过高或者过低都会给用电设备带来安全隐患。潮流分布的不确定性,致使对于节点电压越过限值的情况,若按照传统的调节变压器分接头方法则不能实现准确调节;对于线路过载的情况,若都通过网络重构进行解决,则开关的动作过于频繁[5]。本文通过对分布式电源进行主动控制和管理,调节分布式电源出力实现对配电网潮流的优化,达到控制配电系统节点电压与线路负载率的目的[6]。
电力网络负荷与节点电压的关系是多元的、非线性的,配电网的电压控制是一个难点问题。文献[7-8]通过建立无功优化的非线性多约束数学模型,以分布式电源出力以及无功补偿装置的投切作为变量,利用智能算法进行求解。该类方法的优点是能够得到满足一定目标的无功优化方案,缺点是计算时间过长不适应于实时控制。文献[9-11]提出基于灵敏度分析的电压控制方法,通过计算分布式电源注入节点的有功与无功功率关于节点电压的灵敏度,针对性地改变分布式电源注入节点的功率值,以满足电压幅值要求。在分布式电源渗透率较小的情况下,已有方法没有考虑只通过调节分布电源出力与投切无功补偿装置不能实现对节点电压要求的情况,也没有考虑在线路过载的情况下,通过调节分布式电源出力来减小线路负载率。
网络重构是配电网重要控制手段之一,通过切换联络开关与分段开关的状态实现故障后非故障停电区域的快速复电;线路过载时均衡线路负荷减小线路负载率;节点电压越限时改善电压分布。分布式电源的接入提高了配电网重构可行解数量,降低了重构优化解对应的网络损耗,优化了配电网运行[12]。考虑分布式电源出力不确定性对网络重构的影响,文献[13]利用负荷预测数据,给出未来一天的最优网络拓扑。文献[14]考虑负荷统计分布特点,以及负荷间的相关系数,利用启发式优化算法计算出最优网络重构方案。文献[15]以网络损耗最小以及改善电压分布为目标,利用和声算法求解网络重构的最优拓扑,并利用灵敏度分析确定分布式电源的最优位置。
针对配电网运行中节点电压与线路负载率的实时控制问题,本文提出了基于灵敏度分析的多阶段决策分析方法,仿真一天内负荷及分布式电源出力的变化,在出现节点电压或者线路负载率越限的时刻,给出相应控制措施。
2 电压与负载率控制数学模型
根据智能配电网的断面数据,计算系统潮流,若系统节点电压或者线路负载率越过限值,则通过生成相应简单有效的控制方案,迅速消除系统风险。节点电压与线路负载率的控制目标为系统所有的节点电压幅值偏移量的最大值Vidx与线路负载率的最大值Sjdx皆在安全限值以内,即满足指标函数值δ1=δ2=0,具体计算式为

式中,N为系统节点数目;Nb为系统的支路数目;Vi为节点i的线电压幅值;Si为流过线路i的当前视在功率;Simax为支路可载容量的最大值。
风机以及光伏出力具有很强的不确定性,实时调度时,若一旦指标函数值不满足安全运行要求,就立刻采取控制措施,则会导致控制措施执行过于频繁。在假设负荷以及分布式电源出力可预测前提下(每15min一个预测点),计算相对于当前时刻的未来15min断面潮流,若其节点电压与线路负载率依然不满足安全运行的要求,则执行当前控制方案,否则不执行。
配电网安全运行约束条件包括:
(1)等式约束条件。即系统潮流约束为

(2)分布式电源出力大小的限制为

式中,PG、QG为调节后的分布式电源有功及无功出力;Qmax、Qmin分别为分布式电源无功出力可调节的最大值与最小值;Pmax、Pmin分别为分布式电源有功出力可调节的最大值与最小值。
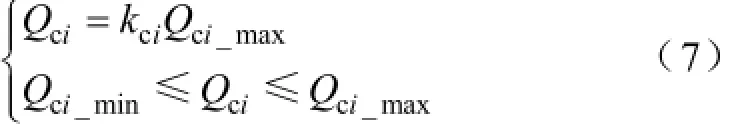
(3)补偿设备容量约束为式中,Qci为第i个无功补偿设备的无功容量,kci为无功补偿设备的档位,Qci_min、Qci_max分别为第i个无功补偿设备的无功容量的最小值与最大值。
(4)网络拓扑约束。不考虑分布式电源,配电网重构前后始终为放射状,即

式中,gk为重构后的网络结构;G为所有可行的辐射状网络结构的集合。
系统若同时出现线路过载与节点电压越限,则优先处理线路过载。整个控制过程参考先易后难,多阶段决策,逐步实现。①阶段一。根据线路过载与节点电压越限两种不同情况,分别计算出相应的灵敏度值,确定分布式电源出力的调节顺序;②阶段二。通过阶段一的控制,若依然不满足安全运行的约束条件,进入网络重构;③阶段三。通过上述两个阶段的控制都无法消除节点电压越限或者线路过载,则通过切除部分非关键负荷使其满足配电网安全运行的要求。
根据国家电网企业标准Q/GDW 480—2010[20]规定,分布式电源总容量原则上不宜超过上一级变压器供电区域内最大负荷的25%。假设单条馈线上分布式电源有功出力小于馈线负荷总有功的50%,满足这一假设前提下的控制流程如图1所示。

图1 控制流程图Fig.1 Flow chart of the control
3 基于灵敏度分析的节点电压与线路负载控制
3.1节点电压控制
对于输电网,忽略电阻与电抗的比值,可近似认为电压只与无功功率相关,当发电机注入节点的无功出力增大时,系统节点电压幅值也增大。但是对于配电网而言,电阻与电抗的比值不可忽略,故若要通过控制分布式电源的出力来调节节点电压,需要同时考虑分布式电源的有功功率与无功功率。
按照注入到节点的功率的类型,分布式电源主要分为四类[16]:①类型1。只注入有功功率P,如光伏、微型燃气轮机以及燃料电池;②类型2。只注入无功功率Q,如燃气同步调相机,甚至无功补偿装置可以当作离散出力的分布式电源;③类型3。同时注入有功功率P与无功功率Q,利用同步发电机进行发电的柴油机与燃气轮机都属于这种类型;④类型4。注入有功功率P,同时消耗无功功率Q,如风力发电机。
图2所示为接有分布式电源的配电网接线示意图。图中Vi表示节点i的节点电压值,Vij表示支路ij的电压降。
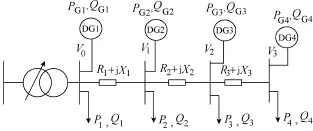
图2 接有分布式电源的配电网示意图Fig.2 Schematic diagram of distribution system with DGs
不考虑分布式电源的情况下,节点3处的节点电压为

式中,I03、R03、X03分别为电流、电阻以及电抗;φ03为功率因数;Ploss、Qloss分别为有功功率与无功功率损耗。
所以对于任意节点m,其节点电压为

式中,Gf为节点0与节点m之间的关联拓扑。
接入分布式电源后,节点m的电压幅值Vm为

由式(11)可知,在一定范围内增大分布式电源的出力,能够有效地改善节点电压。若系统接有M个分布式电源,则节点m的节点电压与M个分布式电源的有功以及无功出力大小有关,通过调节M个分布式电源的有功以及无功出力,可以实现对节点m处的节点电压的控制。节点m的节点电压变化量ΔVm关于M个分布式电源的有功以及无功出力的改变量(ΔP, ΔQ)的灵敏度为

式中,SP、SQ分别为节点电压Vm关于分布式电源功率注入节点i的有功功率与无功功率灵敏度,其值为负数[8],求解推导过程见附录。当节点m的电压值越下限时,向节点i中增大注入功率ΔPi、ΔQi(ΔPi<0,ΔQi<0),ΔVm>0,调节后节点电压升高;反之,减小注入功率ΔPi、ΔQi(ΔPi>0,ΔQi>0),调节后节点m电压减小。灵敏度矩阵反映了节点电压V关于节点注入功率的变化率,即节点电压变化量对功率变化量的灵敏程度。通过控制变量注入功率P与Q就可以调节电压V。通过计算电压越限节点的电压幅值相对分布式电源与无补偿装置节点的注入功率的灵敏度,根据灵敏度值确定分布式电源以及无功补偿装置的功率注入顺序,依次注入功率,直到越限节点的电压值满足安全运行要求,节点电压调节步骤如下:
Step 1:利用牛拉法计算系统潮流,确定电压越限最大值的节点编号a,幅值Va,越上限还是下限,以及灵敏度矩阵SP,SQ。
Step 2:根据灵敏度的值确定分布式电源出力的调节顺序。
Step 3:假设电压越下限,对于确定进行调节的分布式电源,首先假设该装置的剩余功率全部投入,计算投入后Va是否满足,若Va越下限则投入下一个分布式电源;若Va越上限,则改投原来无功功率的1/2,若依然越上限则再减为原来1/2,直到满足约束条件;若改为投原来无功功率的1/2后Va越下限,则增加投入剩余功率的1/2,直到满足约束条件。越上限则恰好相反。
Step 4:当系统中分布式电源的功率全部投入,或者系统中的节点电压都满足运行条件约束时,输出电压控制方案。
3.2线路负载率控制
按照单条馈线上分布式电源有功出力小于馈线负荷总有功50%的假设,对于辐射状配电网,其线路负载率最大的支路依然为馈线首段支路,如图2中的支路1-2。所以只要首段支路的负载率不越限,则辐射状配电网系统不会出现负载率越过限值的线路。设首段线路的电流为I,其允许通过的最大电流为Imax,线路的负载率为ρ,则

接入分布式电源后,首段线路的负载率为
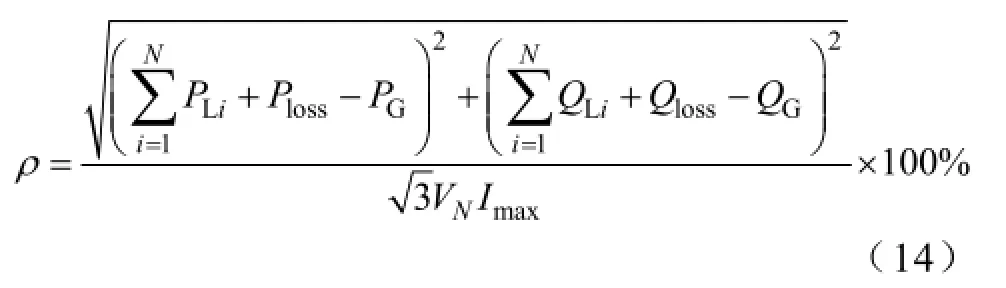
由式(14)可知,在一定范围内增大分布式电源的出力,首段线路的负载率会随着分布式电源出力的增大而减小。

线路负载率控制是指针对当前断面数据,存在电流越上限的支路i,其值为Ii,通过改变注入节点j所安装的分布式电源的ΔS,实现对电流Ii的控制。设功率流出节点为正,即式中,iI′为调节分布式电源出力后支路i的电流,∂|Ii|/∂|Sj|为支路电流Ii关于功率注入节点j的灵敏度,ΔSj为节点j的功率注入量。灵敏度矩阵∂|Ii|/∂|Sj|反映了支路电流I关于节点注入功率ΔS的变化率。首段电流I关于功率注入节点i的注入功率Si= (PGi-PLi)+j(QGi-QLi)的灵敏度为∂|I|/∂|Si|,即

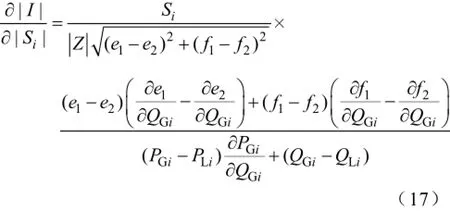
式中,∂e1/∂QGi、∂e2/∂QGi、∂f1/∂QGi、∂f2/∂|QGi可以通过潮流计算获得,∂PGi/∂QGi可由分布式电源的功率因数值求得;e1、e2、f1、f2的值可从潮流计算结果中获取。线路负载率控制步骤如下:
Step 1:利用牛拉法计算系统潮流,确定灵敏度矩阵∂e1/∂QGi,∂e2/∂QGi,∂f1/∂QGi,∂f2/∂QGi的值。
Step 2:根据灵敏度∂|I|/∂|Sj|的值确定分布式电源出力的调节顺序。
Step 3:当系统中分布式电源的功率全部投入,或者系统中的线路负载率都满足运行条件约束时,输出分布式电源的投入顺序。
4 配电网网络重构与切负荷操作
4.1网络重构数学模型与求解
辐射运行的配电网中,闭合任一联络开关都会构成一个回路,断开回路中的任一分段开关,拓扑结构又恢复辐射状。定义由一个联络开关与若干分段开关组成的回路称之为基本环路,基本环路的数目与配电网中联络开关的数目相等。在联络开关数为n,基本环路包含的最大分段开关数为m的辐射状配电网中,定义矩阵M=(mij)n×m,其中,mij为第i个基本环路的第j个分段开关编号,矩阵M的生成算法参考文献[17]。网络重构问题最优解即为搜索矩阵M中每一基本环路的联络开关与分段开关的最优组合,同时保证重构前后系统的拓扑结构保持辐射状。
网络重构的目标函数为

式中,α、β为系数。其中,α+β=1,本文取α=β= 0.5。约束条件见式(4)、式(8)。
组合编码的形式为

式中,xi为第i个联络开关的状态,用二进制进行编码,0表示断开,1表示闭合;SSi表示第i个分段开关编号。按照文献[17]的步骤生成新解,能够有效地避免重构中产生不满足放射状拓扑约束的新解。利用具有编码简单、且能快速实现全局收敛的和声算法进行求解。
4.2切负荷操作
当调节分布式电源出力与网络重构不能消除线路过载或电压越限时,在搜索到最优解基础上进行切负荷,恢复配电网安全运行。切负荷操作的原则为保障系统安全运行的条件下,所切的负荷尽量小,步骤简述如下:
Step 1:将经过调节分布式电源出力与网络重构处理后得到的网络拓扑,从电源点开始将支路进行分层,最接近电源点的所有支路为第一层支路,沿辐射网络向线路末端进行搜索,依次得到其余各层。
Step 2:按层进行遍历,从层数最大的开始。搜索到某一层中某条支路有过载的情况时,确定过载的视在功率ΔS。
Step 3:从过载支路向辐射状的末端开始搜索,将搜索到的负荷按负荷等级分为三类:一级负荷;二级负荷;三级负荷。首先从三级负荷开始切除,选择切除负荷的组合,使所切的负荷量大于等于ΔS,且保证该组合切负荷最小;若只切三级负荷就能满足要求,则该过载支路处理完毕,继续遍历其他支路,若三级负荷全部切除完,也不能满足所切负荷量大于等于ΔS,则切二级负荷,切除的原则与切三级负荷一致,以此类推,到一级负荷。
Step 4:继续按层搜索支路,若存在过载支路,按上一步方法切负荷。直至网络中没有过载线路或所有线路遍历完毕。
5 算例分析
编程仿真环境如下:系统软件Window XP,内存1.9G,Pentium双核,2.60GHz,编程语言Matlab 2009b。和声算法参数初始化,记忆库大小HM=8,HMCR=0.9,PAR=0.2,NI=300。算例为IEEE 33节点系统,母线的额定电压为12.66kV,有33个节点,37条支路,接线图如图3所示,其中联络支路5条,系统总负荷为3 802.19+j2 694.6kV·A。假设线路允许通过的最大负荷为6 000kV·A,详细线路参数以及节点负荷参考文献[18]。Vci=3m/s,Vr=14m/s,Vco=25m/s,其中假设风机的功率因数恒定,取PF=0.9,输出的有功功率Pw与吸收的无功功率Qw的计算式为


图3 IEEE 33节点接线图Fig.3 IEEE 33-node distribution system
分布式电源的接入情况见表1,分布式电源容量的有功部分占负荷的47.34%,满足单条馈线上分布式电源的总有功出力小于馈线负荷总有功功率50%的假设,无功补偿装置的接入情况见表2。

表1 DG安装位置与容量Tab.1 Position and capacity of DGs

表2 无功补偿装置的安装位置与容量Tab.2 Position and capacity of capacitors
考虑一天内负荷、分布式电源出力的变化,对智能配电网的运行进行模拟,针对节点电压与线路负载率越限的情况产生相应的控制策略。设置仿真周期为24h,仿真步长为1h,系统负荷以及风速、光伏出力的变化曲线如图4所示,其中风速的基准值取20m/s,系统负荷的基准值取值见参考文献[18],光伏电池的基准出力取表1中的400kW,各时刻的实际值为基准值乘以图4中各时刻的系数。初始状态为储能(BES)、燃气轮机(MT)、电容器组皆未投入运行。

图4 风速、光伏出力、负荷波动曲线Fig.4 Volatility curve of wind speed, PV output and load
(1)仿真场景1。仿真内容:随着一天内风速、负荷以及光伏出力的变化,按照本文控制方法如何给出相应控制措施,并验证所提出的多阶段决策控制方法的有效性。
图5中黑色曲线为24个时刻的节点电压最小值分布曲线;图6中黑色曲线为24个时刻线路负载率最大值分布曲线。由上述两曲线可知,断面8、9、10、11、15、16、17、18、19、21共10个断面的节点电压最低值都在0.95以下,皆越下限,并且断面19的线路负载率越限,其值大于0.9。

图5 控制前后各时间断面的电压最小值分布曲线Fig.5 Maximin of each section nodal voltage

图6 各次控制执行后各断面的线路负载率Fig.6 Line loading rate profile after each section control
时刻1~7,系统节点电压与线路负载率均满足安全运行要求。时刻8,满足δ1=1,δ2=0(节点电压越下限,负载率不越限,假设其未来15min断面亦不满足安全运行条件),按照多阶段决策控制的流程,首先调节分布式电源出力或者投切无功补偿。通过潮流计算,确定节点电压最低点为节点18,其值为U18=0.944 2,计算节点18关于分布式电源以及无功补偿装置的灵敏度,确定的投入顺序为:储能、燃气轮机、C2,C1,投入储能后系统的电压即满足安全运行条件。其灵敏度的计算如下。
投入储能后的节点18的电压增量为

调节后的电压为

计算储能系统投入后的系统潮流,得到节点18的电压值为0.954 2,两者相差很小,可见利用灵敏度进行调节的误差较小。
时刻8调节后,再次计算24个断面的潮流分布,得到图5蓝色曲线所示各时刻断面的节点电压最低值分布,图6蓝色曲线所示为线路负载率最大值分布。可见,时刻9依然满足δ1=1,δ2=0(节点电压越下限,负载率不越限,假设其未来15min断面亦不满足安全运行条件),触发生成分布式电源与无功补偿的调节方案,按照灵敏度大小确定调节顺序,但是当所有的分布式电源与无功补偿都投入后,节点33的值最低为0.947 1,线路负载率的最大值为0.432 5,系统的节点电压依然不满足指标要求,接着触发网络重构,网络重构的方案见表3。通过上述一系列控制后,整个24个断面的节点电压最低值分布如图5红色曲线所示,线路负载率的最大值分布如图6红色曲线所示。此后,时刻9~17,系统的节点电压与线路负载率皆满足安全运行的要求。

表3 时刻9的网络重构方案Tab.3 Network reconfiguration schemes of moment time 9
到时刻18时,满足δ1=1,δ2=0(节点电压越下限,负载率不越限,假设其未来15min断面亦不满足安全运行条件),此时触发生成控制方案,因分布式电源与无功补偿装置已经全部投入,此时在时刻9已改变的网络拓扑结构的基础上,触发生成网络重构,重构方案见表4。方案执行后,24个时刻断面的最低点电压分布如图5绿色曲线所示,线路负载率的最大值分布如图6中的绿色曲线所示。可见执行时刻18的重构方案后,断面19至断面24都满足安全运行的要求。

表4 时刻18的网络重构方案Tab.4 Network reconfiguration schemes of moment time 18
(2)仿真场景2。为了展示分布式电源的注入对线路负载率的影响,取第一个断面的风速、光伏系数值保持不变,将负荷的系数值改为1.25,致使系统的线路过载,节点电压越下限(即δ1=1,δ2=1)。
根据多阶段决策的流程,首先触发生成分布式电源与无功补偿的调节方案,通过灵敏度分析,确定DGs与电容器组的投入顺序为:C1,燃气轮机,储能,C2。依次投入后线路负载率的变化曲线如图7所示,线路负载率满足了要求,但是节点电压不满足,按照上述控制逻辑,则会生成重构方案,通过网络重构后节点电压满足要求,重构方案见表5,电压分布曲线如图8所示。

图7 依次执行控制措施后各支路的负载率变化曲线Fig.7 Line loading rate curve after control

表5 场景2的网络重构方案Tab.5 Network reconfiguration schemes of scenario 2

图8 依次执行控制措施后各节点的电压幅值变化曲线Fig.8 The nodal voltage curve after control
6 结论
本文提出了一种智能配电网的节点电压与线路负载的实时控制方法,有效融合了调节分布式电源与无功补偿装置,网络重构,以及切除部分非关键负荷的控制措施,通过算例仿真结果得出以下结论:
(1)DGs的广泛接入对配电网产生重大影响,使得调节分布式电源的出力成为控制配电网、优化运行状态的重要手段。
(2)通过灵敏度分析确定DGs与电容器组的投切顺序,使得配电网的电压与负载率控制更加具有针对性,调节误差小,有利于实现以最小的控制代价达到最好的控制效果。
(3)本文通过对一天内负荷、风速以及光伏出力波动性变化的仿真,仿真结果有效验证了控制方案的正确性。
(4)风机、光伏、负荷皆具有很强的不确定性,预测误差相对较大,本文在假设预测相对准确的前提下,计算未来15min的断面潮流作为判断是否执行当前方案标准,研究尚存在一定问题,探索更佳的办法是后续研究重点。
附录
1.节点电压控制灵敏度推导
根据式(11),得

假设调节分布式电源出力时,负荷功率不变,则节点m的电压幅值Um为关于系统所接分布式电源PDGk以及QDGk的函数,即

改变分布式电源的功率大小后,节点m的电压变化为

对于包含N个节点的系统,写成矩阵形式为上式可简化为


式中,SP为注入有功功率灵敏度;SQ为注入无功功率灵敏度。
利用直角坐标系进行潮流计算时,潮流计算方程为

令

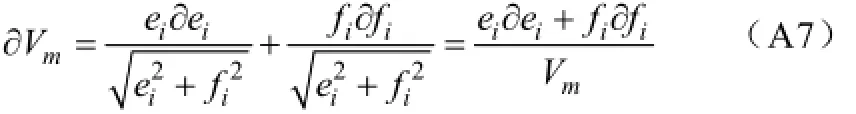
所以
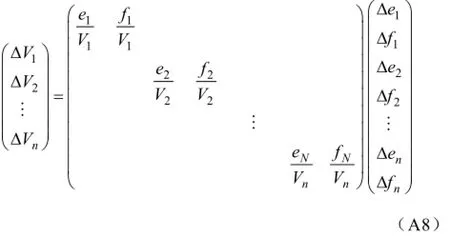
令

调节分布式电源出力时,不考虑负荷变化,则有ΔPDG=ΔP,ΔQDG=ΔQ。根据式(3)、式(4)、式(7)得

2. 线路负载率控制灵敏度推导


[1] 丁明, 王伟胜, 王秀丽, 等. 大规模光伏发电对电力系统影响综述[J]. 中国电机工程学报, 2014, 34(1): 1-14.
[2] Kashem M. Muttaqi, AliEsmaeel Nezhad, Jamshid Aghaei, et al. Control issues of distribution system automation in smartgrids[J]. Renewable and Sustainable Energy Reviews, 2014(37): 386-396.
[3] 王成山, 李鹏. 分布式发电、微网与智能配电网的发展与挑战[J]. 电力系统自动化, 2010, 34(2): 10-23.
[4] Mojtaba Gilvanejad, Hossein Askarian Abyaneh, Kazem Mazlumi. Estimation of the overload-related outages in distribution networks considering the random nature of the electrical loads[J]. IET Generation, Transmission & Distribution, 2013, 7(8): 855-865.
[5] WV YK, LEE CY, LIV LC, et al. Study of reconfiguration for the distribution system with distributed generators[J]. IEEE Trans. Power Delivery, 2010, 25(3): 1678-1685.
[6] 范明天, 张祖平, 苏傲雪, 等. 主动配电系统可行技术的研究[J]. 中国电机工程学报, 2013, 33(22):12-18.
Fan Mingtian, Zhang Zuping, Su Aoxue, et al. Enabling technologies for active distribution systems[J]. Proceedings of the CSEE, 2013, 33(22): 12-18.
[7] 张丽, 徐玉琴, 王增平, 等. 包含分布式电源的配电网无功优化[J]. 电工技术学报, 2011, 26(3): 168-174.
Zhang Li, Xu Yuqin, Wang Zengping, et al. Reactive power optimization for distribution system with distributed generators[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 168-174.
[8] 刘学平, 刘天琪, 李兴源. 含风电机组的配电网无功优化补偿[J]. 电力系统保护与控制, 2010, 38(2):130-135.
Liu Xueping, Liu Tianqi, Li Xingyuan. Optimal reactive power planning in distribution system with wind power generators[J]. Power System Protection and Control, 2010, 38(2): 130-135.
[9] Morris Brenna, Ettore De Berardinis, LVca Delli Carpini, et al. Automatic distributed voltage control algorithm in smart grids applications[J]. IEEE Transactions on Smart Grid, 2013, 4(2): 877-885.
[10] Fabian Tamp, Phil Ciufo. A sensitivity analysis toolkit for the simplification of MV distribution network voltage management[J]. IEEE Transactions On Smart Grid, 2014, 5(2): 559-568.
[11] Muttaqi K M, Le D T, Negnevitsky M, et al. An algebraic approach for determination of dg parameters to support voltage profiles in radial distribution[J]. IEEE Transactions On Smart Grid, 2014, 5(3): 1351-1360.
[12] 王成山, 聂耸, 徐瑞林, 等. 分布式电源接入对配电网络重构影响分析[J]. 天津大学学报, 2014, 47(3): 189-194.
Wang Chengshan, Nie Song, Xu Ruilin, et al. Analysis on the Impact of DG on distribution network reconfiguration[J]. Tianjin University (Science and Technology), 2014, 47(3): 189-194.
[13] 陈春, 汪讽, 黎灿兵, 等. 含分布式风电的配电网预防性重构[J]. 电工技术学报, 2013, 28(9): 172-177.
Chen chun, Wang Feng, Li Canbing, et al. Preventive reconfiguration of distribution networks with distributed wind power[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 172-177.
[14] 刘健, 武晓朦, 余健明. 考虑负荷不确定性和相关性的配电网络重构[J]. 电工技术学报, 2006, 21(12):54-59.
Liu Jian, Wu Xiaomeng, Yu Jianming. Distribution network reconfiguration considering load uncertainty and dependence[J]. Transactions of China Electrotechnical society, 2006, 21(12): 54-59.
[15] Srinivasa Rao R, Ravindra K, Satish K, et al. Narasimham. Power loss minimization in distribution system using network reconfiguration in the presence of distributed generation[J]. IEEE Transactions on Power System 2013, 28(1): 317-325.
[16] Duong Quoc Hung, Nadarajah Mithulananthan, Bansal R C. Analytical expressions for DG allocation in primary distribution networks[J]. IEEE Transactions on Energy Conversion, 2010, 25(3): 814-820.
[17] 陈春, 汪沨, 刘蓓, 等. 基于基本环矩阵与改进和声算法的配电网重构[J]. 电力系统自动化. 2014, 38(6): 55-60.
Chen Chun, Wang Feng, Liu Bei, et al. Network reconfiguration based on basic ring matrix and improved harmony search algorithm[J]. Automation of Electric Power Systems China, 2014, 38(6): 55-60.
[18] Baran M E, Wu F F. Network reconfiguration in distribution systems for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.
[19] James W Taylor, Patrick E McSharry, Roberto Buizza. Wind power density forecasting using ensemble predictions and time series models[J]. IEEE Transactions on Energy Conversion, 2009, 24(3): 775-782.
[20] 国家电网公司企业标准. Q/GDW 480—2010分布式电源接入电网技术规定[S]. 2010.
A Method of Safe Operation Control of Smart Distribution System
Since the installation of distributed generators(DGs) with high penetration, the configuration and power flow profile of distribution system will be changed, and it is necessary to reform the control methods of nodal voltage and line loading rate. A multi-stage decision of sensitivity analysis method is presented in this paper to control the moment time of nodal voltage and line loading rate, and it is organic integration of regulation of output for distributed generators and reactive power compensation device, network reconfiguration, and load shedding. Whether the stage is executed or not based on the value of state function. The variation of load and DGs output within a day is simulated to generate the corresponding control measures of nodal voltage and line loading rate over the limit. The effectiveness of the propose approach is demonstrated by simulations on the improved IEEE 33-nodes systems.
Distributed generations, nodal voltage and line loading rate, multi-stage decision, sensitivity analysis
TM46
陈 春 男,1987年生,博士研究生,主要研究方向为智能配电网运行优化控制。
国家863计划资助项目(2011AA05A114)。
2014-10-13 改稿日期 2015-02-03
Chen Chun1 Wang Feng1 Liu Bei1 Cao Yijia1 Liu Wei3
(1. College of Electrical and Information Engineering Hunan University Changsha 410082 China 2. Jiangxi Electric Power Research Institute Nanchang 330096 China 3. Guangdong Power Grid Corporation CSG. Guangzhou 510080 China)
汪 沨 男,1972年生,教授,博士生导师,主要研究方向为高电压绝缘及气体放电。

