基于改进量子粒子群优化稀疏分解的局放信号去噪方法
王永强 谢 军 律方成
基于改进量子粒子群优化稀疏分解的局放信号去噪方法
王永强 谢 军 律方成
(华北电力大学河北省输变电设备安全防御重点实验室 保定 071001)
噪声抑制是局放在线监测的关键环节之一。针对局放信号噪声抑制问题,提出一种基于改进量子粒子群优化稀疏分解的局放信号去噪方法。该方法基于信号的稀疏分解思想,构建了仅与局放信号时频特性相匹配的匹配局放信号过完备原子库;基于匹配追踪(MP)算法在该原子库中对染噪局放信号进行最佳匹配原子搜索,并通过改进量子粒子群算法加速搜索进程,同时以残差比阈值作为MP迭代终止条件;基于各次MP迭代搜索得到最佳匹配原子仅可对原始无噪局放信号分量进行稀疏表示,而难以对噪声分量进行表示的原理,实现局放信号稀疏分解去噪目的。运用本文介绍方法对局放仿真信号及实测信号进行了去噪处理,并与基于形态学-小波的局放去噪结果作对比。结果表明,本文介绍方法能有效对局放信号进行去噪处理,去噪结果准确性高且波形无畸变,较好保留局放信号原始特征。
改进量子粒子群 稀疏分解 匹配追踪 局部放电 信号去噪
1 引言
局部放电(简称局放)是电气设备绝缘发生劣化的主要征兆,其能有效反映电气设备的绝缘状态,已成为大型电气设备在线监测的主要项目之一[1]。然而由于电气设备运行现场环境复杂,局放监测信号中存在大量的噪声干扰,严重影响监测效果。对局放信号进行有效去噪处理是提高局放监测灵敏度与效果的关键环节之一[1,2-6]。基于小波分析原理的局放信号去噪方法目前使用较多,应用较广,并且取得了不错的效果[2-6]。然而其存在着分解尺度及阈值选择不唯一[5]、难以选取满足局放信号多样性要求的合适小波基函数等缺点[6],这些都直接影响着基于小波理论的局放信号去噪效果。
传统信号表示方法,如小波分析等,通过有限基函数或基向量的集合表示任意信号,但并未充分考虑信号自身特性,故其表示信号的能力尤其是表示形如局部放电等时频范围变化较大的信号的能力是有限的[7],这也影响了基于传统信号表示理论的信号去噪方法其去噪效果[8]。信号的稀疏分解[9]是近年来研究较为热门的一种新型的信号表示方法,其根据信号自身特性,在过完备原子库中自适应选择少量原子对信号进行稀疏表示,避免了传统信号表示方法的缺陷,目前已经较多应用于信号压缩[10]、图像去噪[11]、信号识别[12]等诸多领域。
本文提出一种基于改进量子粒子群优化稀疏分解的局放信号去噪方法。构建了与局放信号时频特征相匹配的过完备原子库,即匹配局放信号过完备原子库;采用匹配追踪(Matching Pursuit,MP)算法在该原子库中对染噪局放信号进行迭代搜索;同时,采用改进量子粒子群算法(Improved Quantumbehaved Particle Swarm Optimization,IQPSO)加速最佳原子搜索进程;由于各次迭代搜索得到的最佳匹配原子可对染噪局放信号中原始无噪信号分量进行稀疏表示,而难以对噪声分量进行表示,进而实现局放信号稀疏分解去噪目的。采用本文方法对仿真与实测信号进行去噪处理,并与基于形态学-小波[13-14]的局放去噪方法去噪结果作对比。结果证明,采用本文方法,能有效抑制局放信号噪声干扰,其去噪效果各项指标均优于传统小波方法,去噪结果误差小,波形无畸变。
2 基于稀疏分解的局放信号去噪方法
2.1信号的稀疏分解及其匹配追踪算法
信号的稀疏分解理论最早由Mallet和Zhang提出[9],其基本原理为:

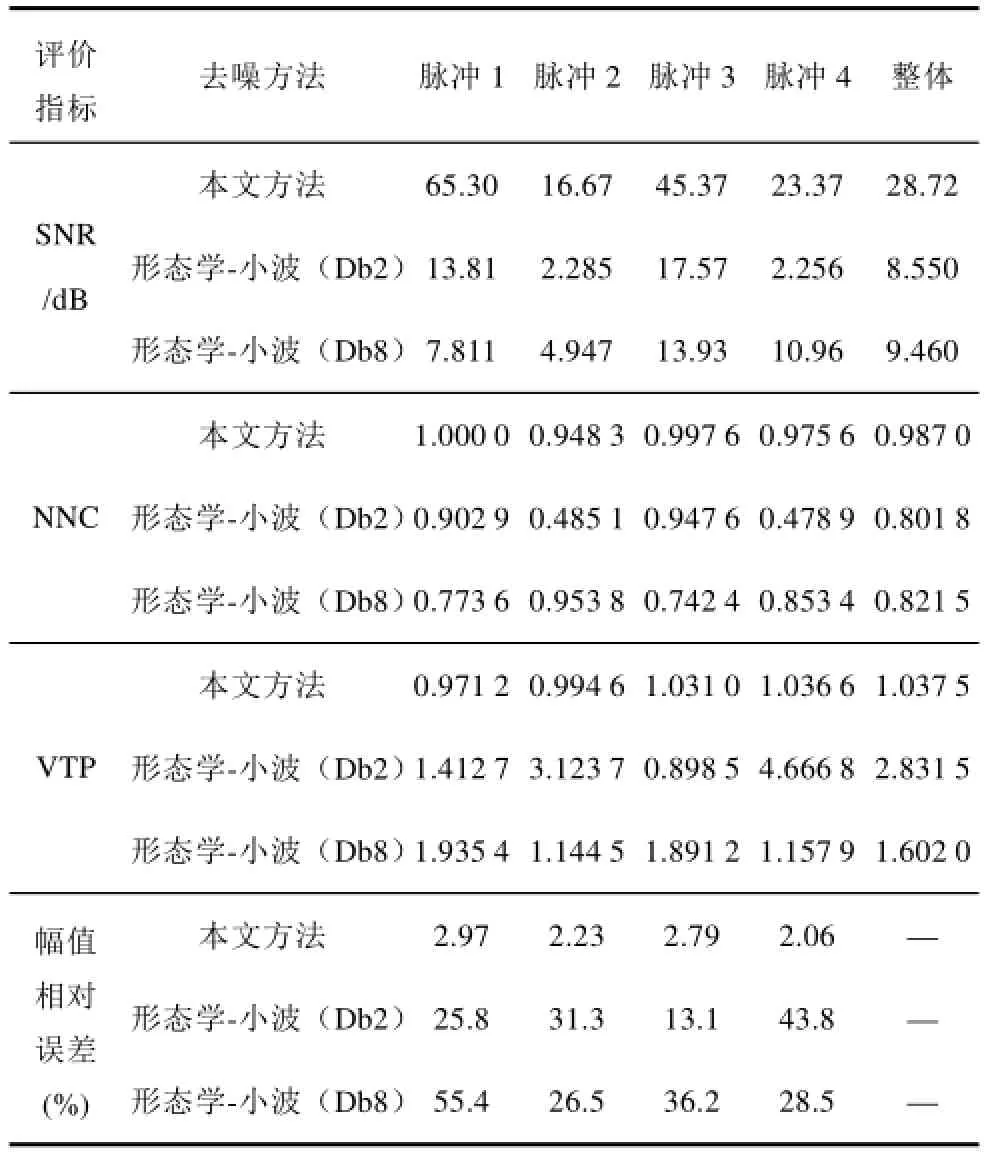
式中,αq为对应原子的展开系数;Im为q的下标集,card(Im)=m,且有m< 匹配追踪(Matching Pursuit,MP)算法[9]是目前信号稀疏分解最常用的方法之一,其基本原理为:首先从过完备原子库D中选取与待分解信号f最为匹配的原子,并满足 式(2)表明,Hilbert空间H=RN中,是该空间最接近信号f方向的原子,即是最能与信号f匹配的原子。故信号f可分解为 令R1f=f,对信号f进行K次分解后,其可表示为 文献[9]研究表明,残差信号的能量会随着K的增大成指数级收敛,并收敛于零。故信号f可稀疏分解为 2.2基于稀疏分解的局放信号去噪方法 对于染噪局放信号,其数学模型可表述为式中,f为染噪局放信号;fp为原始无噪局放信号;fn为噪声信号。 由于无噪局放信号fp是有特定结构的,当构建能充分匹配局放信号特征的过完备原子库D,并在D中对染噪局放信号f进行稀疏分解时,fp的结构特性与D中原子的特性是相关的,fp可用D中原子进行表示;而噪声信号是没有一定的结构或者噪声信号的结构与D中任一原子都难以相关,故噪声信号难以用D中原子表示。因此对染噪局放信号进行基于MP的稀疏分解时,原子与fp的内积就一定大于原子与fn的内积,最先分解出的一定是原始无噪局放信号,用公式表示就是 式(9)中阈值K确定方法,目前主要有硬门限法和软门限法。硬门限法是设定K为常数,其方法简单但误差较大,K过小时丢失无噪信号成分,K过大时又引入噪声成分。软门限法是指当残差信号小于某一阈值时迭代终止,但对于低信噪比的信号,较大的噪声分量会对残差阈值的判断形成影响,进而影响去噪效果[15]。文献[15]介绍了一种基于残差比阈值终止条件,使用残差比阈值终止条件避免了噪声能量较大时,对MP分解残差阈值的判定影响,减少了噪声干扰,提高了稀疏分解的鲁棒性。 设Rkf、Rk+1f分别为第k次与第k+1次残差值,则残差比())k qRf为 2.3匹配局放信号过完备原子库 如前文所述,对染噪信号进行基于MP算法的稀疏分解,进而成功实现去噪效果的关键是过完备原子库中各原子与局放信号特征相匹配而与噪声信号不相关。基于此,本文提出了一种局放脉冲匹配原子,并由此类原子构建了匹配局放信号过完备原子库。 由于故障位置、放电机理、放电设备等不同,局放信号呈现出多样性,局放信号通常可由以下四种数学模型表示[16]。 (1)单指数衰减模型。即 (2)单指数振荡衰减模型。即 (3)双指数衰减模型。即 (4)双指数振荡衰减模型。即 式中,τ为衰减常数;fc为振荡常数。 总结分析四种局放波冲信号的波形特性,本文构造局放脉冲匹配原子为 式中,γ为原子参数,每个局放脉冲匹配原子包含五个参数γ=(u,β,s ,ω,φ):u为位移因子;β 为波形因子;s为尺度因子;ω为频率因子;φ为相位因子。kn为归一化系数,其使原子满足归一化条件。ρ为衰减修正系数,此系数用于避免当s较大时局放脉冲匹配原子与正弦信号相匹配,以有效去除窄带周期干扰对局放信号的影响。 设局放离散信号采样长度为N,对原子参数γ=(u,β,s ,ω,φ)进行离散化,其具体方法为:γ=(nu,nβ,ns,2πnω/N,3πnφ/2),nu∈[0,N-1],nβ∈[0,1],ns∈[1,N],nω∈[0,N -1],nφ=[0,1],且有nu,nβ,ns, nω,nφ∈Z。得到离散化局放脉冲匹配原子为 对上式进一步分析,可知 (1)当nω=0,nφ=0时,式(16)化为 此时,该类原子与式(11)及式(13)表示的指数衰减型局放信号模型相匹配。 (2)当nφ=1时,式(16)化为 该类原子与式(12)及式(14)表示的振荡衰减型局放信号模型相匹配。综上,本文所提局放脉冲匹配原子能很好的与各类型理想局放信号相匹配。 根据局放脉冲匹配原子离散化原子参数取值不同,共可生成4N3个长度为N的局放脉冲匹配原子,且有4N3≥N,满足过完备字典冗余性要求,故可将此类原子构成匹配局放信号过完备原子库Dp,长度为N的局放信号可在此过完备原子库中进行稀疏分解进而达到去噪效果。 3.1量子粒子群算法简介 MP算法从匹配局放信号过完备原子库中搜索最佳局放脉冲匹配原子,每一次过程都要完成多参数优化问题。由于与长度为N的局放信号相匹配的匹配局放信号过完备原子库其原子数目为4N3,因此,传统的MP算法计算量将是巨大的。 Sun等人将粒子群算法(Particle Swarm Optimization,PSO)同量子理论相结合,提出量子粒子群优化算法(Quantum-behaved Particle Swarm Optimization,QPSO)[17]。相比PSO算法,QPSO可在整个可行域内进行寻优,其全局收敛能力大大提高,且以概率1收敛[18]。QPSO算法采用量子学中波函数描述粒子位置,通过求解薛定谔方程得到粒子在空间某一位置的概率密度函数,并由蒙特卡罗随机模拟得到粒子位置方程 式中,±号取值概率相等;gbest(t)为到t代时,粒子的个体最优位置,gbest为种群的全局最优位置;p为吸引子,且有 C(t)为到t代时,粒子个体平均最优位置,即 式中,M为粒子数目。 式(19)中,α为收缩扩张系数,其是QPSO算法中唯一的参数。当α较大时,此时粒子搜索空间较大,算法收敛速度较快但精度不高;α较小时,此时算法精度较高但收敛较慢。一般随着迭代次数增加,α设置为线性递减,使算法初期收敛较快而后期收敛精度提高[17-18]。 3.2改进量子粒子群算法 传统QPSO算法其收缩扩张系数是线性递减的,这种α确定方法独立于算法本身较为固定,但实际搜索过程往往是非线性的且高度复杂的,α应能反映粒子运行过程中的实际状况而自适应变化,而且使用传统的QPSO算法也存在着易陷入局部最优的缺陷[17]。基于MP算法的最佳原子寻优这一实际问题,本文提出了基于自适应收缩扩张系数结合混沌扰动的改进量子粒子群算法(Improved Quantumbehaved Particle Swarm Optimization,IQPSO),提高收敛速度与收敛精度,防止算法陷入局部最优。 以局放脉冲匹配原子其原子参数为待寻优参数组,以原局放信号或其残差信号与原子的内积绝对值为适应度函数f。定义进化速度因子为 式中,f(gbest(t-1))与f(gbest(t))分别为第t-1次与第t次全局最优位置的适应度值。 由于全局最优位置随着迭代进行总是保持或更新,即f(gbest(t))>> f(gbest(t-1))>0,故v∈(0,1]。 对进化速度因子进行分析可知:v值较小时,全局最优位置适应度值变化较大,此时进化较快; v值较大时,此时进化较慢;v=1时,进化停止。当进化速度较快v较小时,粒子距最优位置较远,此时粒子应有较大的搜索范围即提高α值以快速寻优;当进化速度较慢v较大时,粒子靠近最优位置,此时应减小粒子搜索范围即减小α值以精确寻优。考虑到实际进化过程影响,本文提出的基于粒子进化速度因子的自适应收缩扩张因子为式中,α0为α初值,一般取1;α1为速度因子权重,一般取0.5,则[0.5,1] α∈。 同时为了进一步避免算法陷入局部最优,当全f(gbest(t))连续数次停止更新时,对粒子进行如下混沌变异操作: (1)将粒子位置映射到区间[0,1]内,即 (2)对X′进行Logistic混沌运算[19],即 式中,Xmax、Xmin分别为粒子寻优范围上下限。 3.3基于改进量子粒子群优化稀疏分解的局放信号 去噪方法具体步骤 基于改进量子粒子群优化稀疏分解的局放信号去噪方法具体步骤如下: (1)以原局放信号或残差信号与原子的内积作为适应度函数,以局放脉冲匹配原子其原子参数为待寻优参数组。确(3)将X′重新映射到X的寻优范围内,即定种群规模n、IQPSO最大迭代次数T、允许最大迭代停止更新次数M。 (2)对染噪局放信号或其残差信号进行MP分解,根据各原子参数范围对种群进行初始化,置当前迭代停止更新累计次数N=1。 (3)计算各粒子的适应度值,比较并更新记录各粒子的个体历史最优适应度值及位置,比较并更新记录全局历史最优适应度值及位置。 (4)若迭代次数t=1,则收缩扩张因子α=1,若t≥2,则计算进化速度因子v并自适应更新收缩扩张因子α。 (5)若v=1,则N=N+1;若N<M,则根据量子粒子群进化方法对粒子进行进化操作;若N=M,则对粒子位置进行混沌变异操作,并对N进行初始化即N=1。 (6)判断是否满足IQPSO迭代终止条件,若不满足则转到步骤(3);若满足则得到该次迭代最优局放脉冲匹配原子。计算并保存残差信号 式中,k为MP迭代次数。 (7)根据残差比阈值条件,确定是否满足MP计算迭代终止条件,若不满足则返回步骤(2)并代入步骤(6)生成的新残差信号重复上述过程,若满足则去噪结束。去噪后局放信号为 4.1局放信号仿真 为了验证本文所提局放去噪方法的有效性,对局放仿真信号进行了去噪处理。图2a为理想局放信号仿真波形,该信号共含四个局放脉冲波形,从左至右依次为单指数衰减型脉冲、单指数振荡衰减型脉冲、双指数衰减型脉冲、双指数振荡衰减型脉冲。衰减常数τ为1.3μs,振荡常数fc为1.2MHz,信号采样频率fs为20MHz,采样时间为200μs,各局放脉冲幅值归一化为1。在理想局放仿真信号加入噪声以模拟含噪局放信号,噪声主要包括局放信号干扰中常见的白噪声随机干扰及窄带干扰。其中局放白噪声随机干扰采用(0,0.32)分布的高斯白噪声信号模拟;局放窄带干扰采用归一化幅值为0.2,频率分别100kHz、300kHz、500kHz、1MHz及2 MHz的正弦信号模拟。染噪局放仿真信号波形如图2b所示,经计算该信号信噪比为-8.2 dB。 图1 局部放电仿真信号Fig.1 PD simulation signal 4.2去噪结果分析 采用本文介绍方法对染噪局放信号进行去噪处理。其中,初始种群数目为50,IQPSO最大进化次数为400,最大允许迭代停止更新次数为10。其去噪结果如图4a所示。 为了对比说明本文方法去噪效果,本文选择形态学-小波综合去噪方法[13-14]对该仿真信号进行去噪处理。该方法利用数学形态学滤波器在频域滤除窄带干扰信号离散谱线,同时保留局放信号特征谱线以抑制局放窄带周期性干扰;采用小波方法抑制局放白噪声随机噪声干扰。其中形态学滤波器基于最小均方(LSM)原理由形态学开、闭组合而成,其结构元素自适应[14];小波包分别选择目前应用于局放去噪领域较多的Db2与Db8小波[5],其去噪结果分别如图2b、图2c所示。 图2 局放仿真信号去噪结果Fig.2 PD simulation signal denoising results 引入信噪比(Signal to Noise Rator,SNR),波形相似系数(Normalized Correlation Coefficient,NCC),变化趋势参数(Variation Trend Parameter,VTP)及幅值相对误差等作为局放信号去噪效果评价指标。其中,NCC用于评价去噪后局放恢复信号与原理想局放信号波形相似程度,其取值为[-1,1],且越接近1两者波形越相似;VTP代表两波形振荡变化趋势相似度,其值越接近1,两波形振荡变化趋势也就越相似。各评价指标具体定义及计算方法可见文献[20]。分别计算上述三种局放去噪方法去噪效果评价指标,其结果如表1所示。 表1 去噪效果评价指标计算结果Tab.1 Calculation results of denoising performance parameters 综合图2及表1结果,对比三种方法去噪结果及去噪效果评价指标,可得如下结论: (1)本文介绍的基于改进量子粒子群优化的局放信号稀疏分解去噪方法,其去噪前后各脉冲时域波形未发生明显畸变,波形及波形振荡趋势保持不变,幅值误差最小,去噪后恢复信号噪声含量最低,各局放脉冲去噪效果评价参数最优,去噪效果明显优于另外两种方法。 (3)基于形态学-小波的局放信号去噪方法,去噪后信号与原局放信号相比,幅值均有误差且波形均有畸变。本次仿真结果表明,若选择Db2小波,则对指数衰减型局放信号去噪效果较好,对于振荡衰减型信号去噪效果明显降低;若选择Db8小波,对于振荡衰减型局放信号去噪效果较好,但对指数衰减型信号去噪效果较差。 进一步分析可知,小波方法通过小波基伸缩变换逼近待分析信号,选用不同小波基,其去噪效果将会有明显不同,当小波基的形状与待分析信号差异较大时,很难获得理想去噪效果;同时小波分解层数及阈值选择均会对去噪效果产生影响[6,21]。究其原因,主要是因为小波分析的实质通过有限基函数或基向量的集合表示任意信号,却并未充分考虑信号自身特性,而且该基函数或基向量的组合描述信号的能力也是有限的,故其表示形如局部放电等时频范围变化较大的信号能力是有限的,因此也影响了基于小波分析理论的局放去噪方法去噪效果。 本文所提局放信号去噪方法,其实质是信号的稀疏分解,由于匹配局放信号过完备原子库的冗余特性,其基本涵盖了局放信号时频范围的所有特征,基于匹配追踪算法选取少量原子对局放信号进行稀疏分解及稀疏表示,实现了对原无噪局放信号的精确重构,即实现了含噪局放信号的高效去噪,故本文方法取得较好去噪效果。同时,本文采用IQPSO算法,仅需对种群中各个体数据进行保存,进而迭代更新以得到最优原子,克服了传统MP算法需对所有原子参数进行保存而使得存储量大的问题。 图3为采用本文方法对仿真局放信号去噪前后各局放脉冲波形对比图,其中虚线为局放原始信号,实线为局放去噪恢复信号(即各最佳局放脉冲匹配原子波形,两者仅为幅值差别)。 图3 去噪前后各局放脉冲波形对比图Fig.3 Comparisons of every PD pulses before and after denoising 由图3可进一步看出,采用本文方法局放去噪结果准确性高及波形无畸变的特点;最佳局放脉冲匹配原子波形与各局放脉冲信号波形一致,通过原子参数能准确得到局放信号主要特征参数,这些特征参数可为后续局放信号分析提供重要依据。当然,这需要后续大量理论与实验的分析与验证。 图4为采用传统QPSO算法和本文所提IQPSO算法进行MP最佳匹配原子搜索时,适应值收敛曲线。其中纵坐标为是适应值即内积数值,横坐标为种群迭代更新次数,虚线为采用传统QPSO算法,实线为本文所提IQPSO算法。 图4 QPSO算法与IQPSO算法收敛效果对比图Fig.4 QPSO and IQPSO convergence effect comparison chart 由图4可知,由于噪声的影响,MP寻优存在着局部最优值,QPSO算法易于陷入局部最优而难以找到全局最优,本文采用的混沌变异操作有效克服局部收敛对MP寻优结果的影响,易于得到全局最优;同时,本文根据寻优函数自身特性采用自适应收缩扩张系数,使算法收敛速度更快。故本文所提IQPSO算法有效提高最佳原子搜索速度与效果。 5.1实验室实测信号验证 在实验室中采用在变压器油中放置尖端放电模型来模拟绝缘缺陷以获得实测局放信号,如图5所示。其中,尖端放电模型针电极曲率半径为0.5mm,锥角70°,尖长35mm,上下极间距为12mm。 图5 尖端放电模型Fig.5 Tip discharge model 图6 为实验室中采用上述放电模型得到的两局放信号实测波形,其幅值进行归一化处理,采样频率为25MHz。由于实验室干扰较弱,局放原始信号可较容易区分,本文采取测量实验室本底噪声并放大叠加到局放实测信号中以模拟含噪局放信号,其波形如图7所示。 图6 实验室测量局放信号Fig.6 Laboratory measured PD signals 图7 加入噪声后实验室局放测量信号Fig.7 Laboratory measured PD signals with noise 采用本文介绍方法对上述含噪局放信号进行去噪处理,去噪结果如图8a所示。同时,本文一并给出采用基于Db2小波与Db8小波的形态学-小波方法去噪结果,分别如图8b、图8c所示。 图8 实验室实测局放信号去噪结果Fig.8 Laboratory measured PD signals denoising results 由于原始局放测量信号噪声干扰较小,可将其近似等效为理想无噪局放波形,计算各方法去噪效果评价指标,其结果如表2所示。 表2 实验室实测局放信号去噪效果评价指标Tab.2 Laboratory measured PD signal denoising performance parameters 综合图8及表2结果,三种方法均能对实验室实测染噪局放信号进行恢复,但采用小波方法其去噪结果能量损失较大,且波形有较大畸变,去噪效果较差;本文介绍局放信号去噪方法噪结果准确性高,波形无畸变,较好保留了原始局放信号局部特征,且去噪效果评价指标如NCC、VTP等接近于理想值1,其去噪效果明显优于小波方法。 5.2现场实测信号验证 图9为现场某变电站实测局放原始信号,采样频率为10MHz。由于现场噪声水平较高,局放信号已被严重干扰,某些幅值较小局放脉冲甚至淹没于噪声之中难以区分。 图9 现场实测局放信号Fig.9 Field partial discharge signal 采用本文介绍方法对该实测信号进行去噪处理,其结果如图10所示,由图可知,本文算法能有效将现场含有大量噪声的局放信号提取出来。 图10 实测局放信号去噪结果Fig.10 Field partial discharge signal Denoising result 由于无法得到不含噪声的实测局放信号,故无法计算NCC、VTP等去噪效果评价指标,可采用噪声抑制比[14]进行去噪效果评价,其定义为 式中,σ1、σ2为去噪前后信号偏差。ρNRR反映了去噪后有效信号的凸显程度。经计算,采用本文介绍方法去噪结果其噪声抑制比ρNRR为21.07,这说明,本文算法对现场局放信号噪声抑制具有较好效果。 本文提出一种基于改进量子粒子群优化稀疏分解的局放信号去噪方法,并通过仿真及实测信号验证了该方法的有效性。本文结论如下: (1)对染噪局放信号进行MP计算,在匹配局放信号过完备原子库中自适应选取少量原子,可实现对原始无噪局放信号分量稀疏表示,而难以对噪声分量稀疏表示,进而实现去噪效果。 (2)引入了进化速度因子,实现收缩扩张系数根据算法自身进化情况自适应更新;采用了混沌变异操作,防止粒子陷入局部最优。本文所提改进量子粒子群算法有效提高最佳原子搜索速度与效果。 (3)对仿真信号及实测信号的去噪效果表明:本文介绍方法其去噪效果各项指标均优于传统小波方法,去噪结果准确性高且波形无畸变,较好保留局放信号特征,便于后续分析。 [1] 王昌长, 李福琪, 高胜友. 电力设备的在线监测与故障诊断[M]. 北京: 中国电力出版社, 2006. [2] 杨霁, 李剑, 王有元, 等. 变压器局部放电监测中的小波去噪方法[J]. 重庆大学学报, 2004, 27(10): 67-70. Yang Ji, Li Jian, Wang Youyuan, et al. Application of wavelet denoising in partial discharge online monitoring of transformer[J]. Journal of Chongqing University, 2004, 27(10): 67-70. [3] 尚海昆, 苑津莎, 王瑜, 等. 平移不变小波迹消噪方法在局部放电检测中的应用[J]. 电工技术学报, 2013, 28(10): 33-40. Shang Haikun, Yun Jinsha, Wang Yu. Application of wavelet footprints based on translation-invariant in of partial discharge signal detection[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 33-40. [4] Dey D, Chatterjee B, Chakravorti S, et al. Crosswavelet transform as a new paradigm for feature extraction from noisy partial discharge pulses[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(1): 157-166. [5] 江天炎, 李剑, 杜林, 等. 粒子群优化小波自适应阈值法用于局部放电去噪[J]. 电工技术学报, 2012, 27(5): 77-83. Jiang Tianyan, Li Jian, Du Lin, et al. Denoising for partial discharge signals using PSO adaptive wavelet threshold estimation[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 77-83. [6] 钱勇, 黄成军, 陈陈, 等. 多小波消噪算法在局部放电检测中的应用[J].中国电机工程学报, 2007, 27(6): 89-95. Qian Yong, Huang Chengjun, Chen Chen, et al. Application of multi-wavelet based on denoising algorithm in partial discharge detection[J]. Proceedings of the CSEE, 2007, 27(6): 89-95. [7] 朱明. 复杂体制雷达辐射源信号时频原子特征研究[D]. 成都, 西南交通大学, 2008. [8] 罗勇江. 宽带数字侦察接收机若干关健技术研究及应用[D]. 西安, 西安电子科技大学, 2012. [9] Mallat S. G, Zhang Zhifeng. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. [10] 宋蓓蓓, 孙文方. 基于稀疏重建的压缩图像质量提高方法[J]. 华中科技大学学报(自然科学版), 2012, 40(9): 30-33, 43. Song Beibei, Sun Wenfang. Compression image quality improvement via sparse reconstruction[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(9): 30-33, 43. [11] Protter M, Elad M.Image sequence denoising via sparse and redundant representations[J]. IEEE Transactions on Image Processing, 2009, 18(1): 27-35. [12] John Wright, Allen Y. Yang, Arvind Ganesh, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. [13] 刘云鹏, 律方成, 李成榕, 等. 形态学一小波综合滤波器抑制局放现场干扰[J]. 高电压技术, 2004, 30(2): 29-31. Liu Yunpeng, Lü Fangcheng, Li Chengrong, et al. Study of novel integrated morphology-wavelet filter in suppressing PD’s field noise[J]. High Voltage Engineering, 2004, 30(2): 29-31. [14] 刘云鹏, 律方成, 李成榕, 等. 基于数学形态滤波器抑制局部放电窄带周期性干扰的研究[J]. 中国电机工程学报, 2004, 24(3): 169-173. Liu Yunpeng, Lü Fangcheng, Li Chengrong, et al. Study of the mathematical morphological filter in suppressing periodic narrow bandwidth noise of PD[J]. Proceedings of the CSEE, 2004, 24(3): 169-173. [15] 梁巍, 阙沛文, 陈亮, 等. 基于残差比阈值的迭代终止条件匹配追踪稀疏分解方法[J]. 上海交通大学学报, 2010, 2(44): 171-175. Liang wei, Que Peiwen, Chen Liang, et al. Residual ratio iteration termination condition for MP method[J]. Journal of Shanghai Jiaotong University, 2010, 2(44): 171-175. [16] 黄成军, 郁惟镛. 基于小波分解的自适应滤波算法在抑制局部放电窄带周期干扰中的应用[J]. 中国电机工程学报, 2003, 23(1): 107-111. Huang Chengjun, Yu Weiyong. Study of adaptivefilter algorithm based on wavelet analysis in suppressing PD’s periodic narrow bandwidth noise[J]. Proceedings of the CSEE, 2003, 23(1): 107-111. [17] Sun J, Feng B, Xu W. Particle swarm optimization with particles having quantum behavior[C]. Congress on Evolutionary Computation, Portland, USA, 2004: 325-331. [18] 方伟, 孙俊, 谢振平. 量子粒子群优化算法的收敛性分析及控制参数研究[J]. 物理学报, 2010, 59(6): 3686-3694. Fang Wei, Sun Jun, Xie Zhenping. Convergence analysis of quantum behaved particle swarm optimization algorithm and study on its control parameter[J]. Acta Physica Sinica, 2010, 59(6): 3686-3694. [19] 朱敏, 杨春玲. 基于混沌序列的时序数字电路BIST技术[J]. 电工技术学报, 2010, 25(6): 144-149. Zhu Min, Yang Chunling. BIST technique of sequential circuits based on chaotic sequence[J]. Transactions of China Electrotechnical Society, 2010, 25(6): 144-149. [20] 唐炬, 高丽, 彭莉, 等. 非平稳振荡局放信号去噪效果评价参数研究[J]. 高电压技术, 2007, 33(12): 66-70. Tang Ju, Gao Li, Peng Li, et al. Study on new evaluation parameters for denoising performance of non- stationary oscillating partial discharge signals[J]. High Voltage Engineering, 2007, 33(12): 66-70. [21] 李天云, 高磊, 聂永辉. 基于经验模式分解处理局部放电数据的自适应直接阈值算法[J]. 中国电机工程学报, 2006, 26(15): 29-34. Li Tianyun, GaoLei, Nei Yonghui. A new adaptive direct-threshold algorithm to partial discharge data processing based on empirical mode decomposition[J]. Proceedings of the CSEE, 2006, 26(15): 29-34. PD Signal Denoising Method Based on Improved Quantum-Behaved Particle Swarm Optimization Sparse Decomposition Wang Yongqiang Xie Jun Lü Fangcheng Noise suppression is one of the key links for partial discharge(PD) online monitoring. Focusing on the noise suppression, a PD signal denoising method based on improved quantum-behaved particle swarm optimization sparse decomposition was given in this paper. More specifically, the principle of this method is signal sparse decomposition. The partial discharge signal matching overcomplete dictionary which only matches the features of PD signals was built. Based upon these, polluted PD signal was sparse decomposed by matching pursuit(MP) algorithm in this dictionary to search the best matching atoms. Meanwhile, the improved quantum-behaved particle swarm optimization(IQPSO) was presented to accelerate the searching process, and the residual ratio was chosen to be the terminating condition of the iteration as well. Since no noise PD signal component can be sparse represented by the best atoms while the noise cannot, the goal of denoising was finally achieved. The denoising method presented in this article is applied on the simulated and measuring signals, the results are critical compared with the effect of the PD denoising method based on the morphological wavelet, the results show that the denoising method of this paper is available to precisely suppress the noise interference of PD signal with high accuracy results; the distortion of waveform after denoising cannot be found and the features of PD signal were well kept. Improved quantum-behaved particle swarm optimization(IQPSO), sparse decomposition, matching pursuit(MP), partial discharge(PD), denoising TM835 王永强 男,1975年生,博士,副教授,研究方向电气设备在线监测与故障诊断。 国家高技术研究发展计划(863计划)(2012AA050802)、国家电网资助项目(GY17201200047)和中央高校基金(13MS73)资助项目。 2014-04-14 改稿日期 2014-06-17 谢 军 男,1988年生,博士研究生,研究方向为电气设备在线监测与故障诊断。
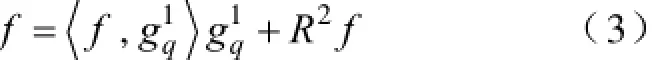



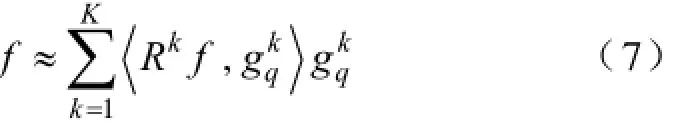







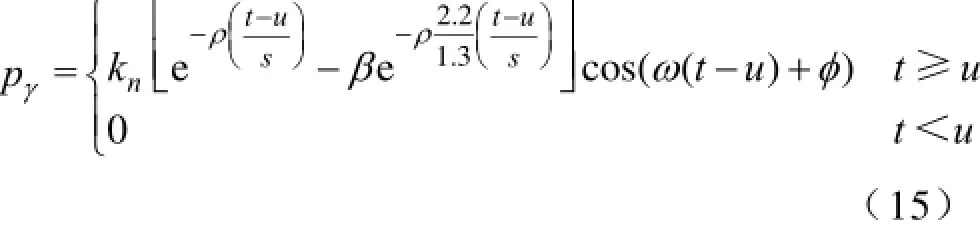


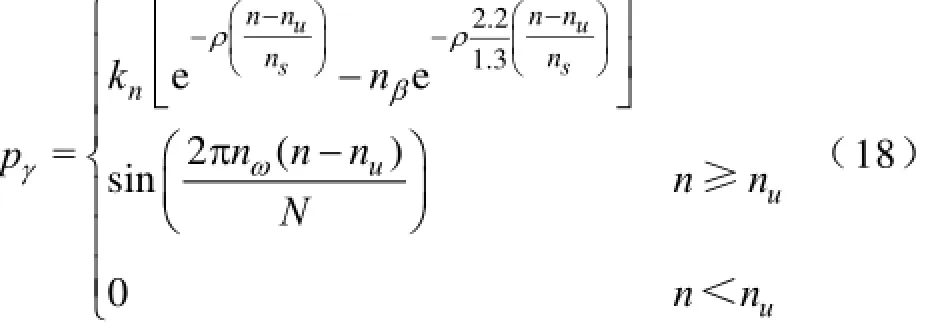
3 基于改进量子粒子群算法的最佳匹配原子搜索方法



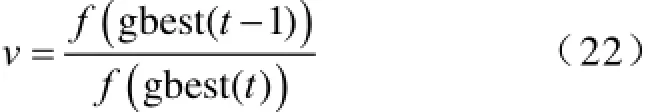



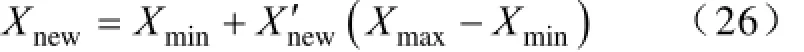
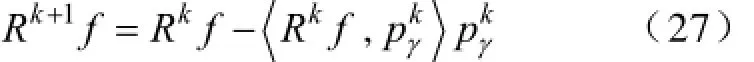

4 仿真验证与分析





5 实测信号验证








6 结论
(Hebei Provincial Key Laboratory of Power Transmission Equipment Security Defense
North China Electric Power University Baoding 071003 China)

