永磁球形电动机永磁体涡流损耗分析

李洪凤 沈彦波

永磁球形电动机永磁体涡流损耗分析

李洪凤 沈彦波

（天津大学电气与自动化工程学院 天津 300072）

永磁球形电动机的磁极呈球面锥体结构，各定子线圈相互独立分布于定子球壳内表面，针对这些特性，提出了一种计算永磁球形电动机永磁体涡流损耗的三维解析模型。该模型将双重傅里叶级数法与矢量磁位解析法相结合，首先利用双重傅里叶级数法求得定子内径处电流密度分布，继而将其作为边界条件，借助三维拉普拉斯方程，获得了矢量磁位的特解，最后推导得到了永磁球形电动机永磁体涡流损耗的解析表达式。该模型充分考虑到了时间谐波与空间谐波对涡流损耗的影响，并分析了不同的电机结构参数对永磁体涡流损耗的影响。将解析法与有限元法所得结果进行了比较，结果一致，证明了该解析模型的有效性。

永磁球形电动机 双重傅里叶级数法 矢量磁位法 永磁体涡流损耗解析模型

1 引言

目前，机械手、机器人等装置多自由度运动的实现需要多台单自由度电机的相互配合，但是，这样的系统具有体积大、精度低、摩擦大等缺点。为了改善系统的性能，国内外的学者将研究的重点放到了单轴可以实现多自由度运动的电动机上。其中，永磁球形电动机以体积小、重量轻、力能指标高、控制简单等优点，成为多自由度电动机研究的热点[1-9]。

永磁体的涡流损耗是永磁球形电动机设计的一个关键性问题。现阶段，永磁体大多采用钕铁硼， 这是因为其具有较高的矫顽力和剩磁，但其电导率比较高且耐热性差，涡流会使永磁体发热并升温，甚至会导致部分不可逆退磁。纵观国内外学者关于永磁体涡流损耗的研究，本质上主要局限于采用解析法和有限元法对传统单自由度永磁电动机永磁体涡流损耗二维模型进行的分析[10-16]。其中，文献[10]将定子线圈电流等效为位于定子槽口处的等效电流片。还考虑了空间谐波分量和时间谐波分量对涡流损耗的影响，给出了解析表达式，并与有限元仿真进行了比较，验证了解析表达式的正确性。文献[11]通过对理论推导和实验进行比较，得出了将永磁体分为多个单元并进行相互隔离时能够减小永磁体中产生涡流损耗的结论。文献[12]应用解析法分析了永磁同步电机带交、直流负载时的涡流损耗情况，为如何降低带载时的转子涡流损耗提供了宝贵的数据材料。文献[13]对比分析了永磁体涡流损耗对电动机与发电机的温升的影响情况。文献[14]利用数值方法，计算了发电机在三相负载不对称时负序电流在转子上产生的涡流损耗以及由涡流损耗引起的温升。文献[15]则考虑了PWM调制对无刷直流电机转子的涡流损耗的影响，通过改变占空比，分析了涡流损耗的变化情况。

本文的研究对象的实物模型如图1所示，定子线圈被分为3层，每层18个线圈，6块永磁体按N极与S极交替安装在球形转子上，各结构名称如表1所示。首先，应用双重傅里叶级数法推导得到了定子线圈的等效电流片的电流密度分布。其次，采用解析法，以矢量磁位为求解变量，对永磁体涡流损耗进行了理论推导，得到了永磁体涡流损耗的解析表达式，最后用有限元法验证了解析方法的正确性。

图1 永磁球形电动机实物模型Fig.1 The prototype of the PMSM

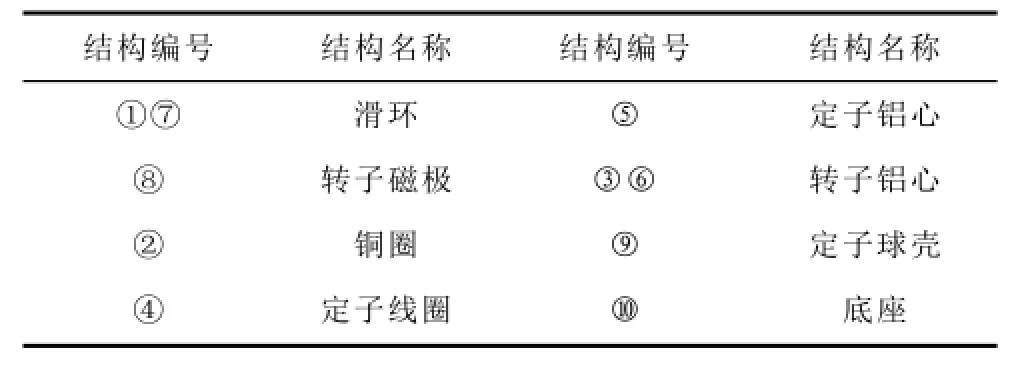
表1 结构名称Tab.1 The names of different structures

2 定子线圈电流密度分布

为了计算永磁球形电动机永磁体的涡流损耗，需要计算出定子线圈在气隙与永磁体内的电磁场分布，而这需要得到线圈在定子内径处的电流密度分布。

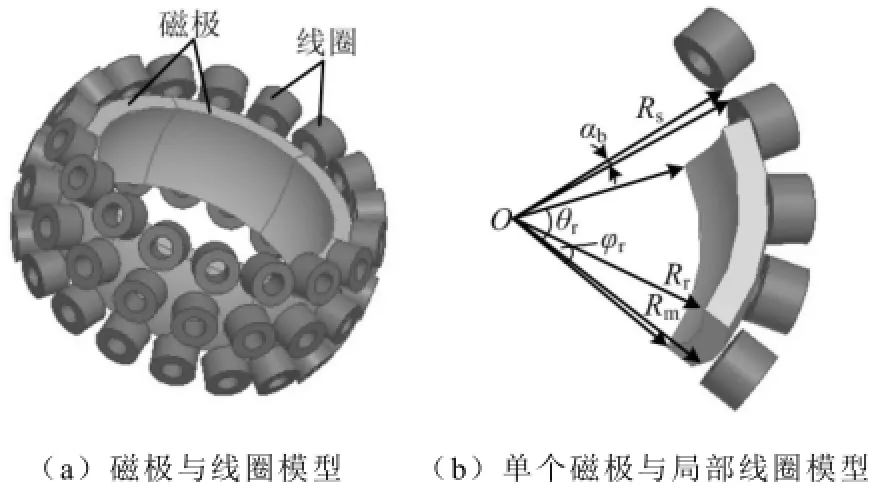
图2 永磁球形电动机的三维模型Fig.2 The 3-D model of the PMSM

图2 (a)给出了电机全部磁极与线圈的三维模型，图2(b)给出了单个磁极与局部线圈模型，其中Rs、Rm和Rr分别为定子内径、磁极外径和磁极内径，αb表示线圈间隙对应机械角度，θr为单个磁极的经度角，φr为单个磁极的纬度角，O为球心。假设把电机的三层线圈沿定子周向延展开，将圆形线圈电流等效为位于线圈间隙间的厚度无穷小的圆环状电流片，由于存在α，φ两个变量，需要应用到双重傅里叶变换对等效电流片电流密度进行分析。为了简化分析，进一步将圆环状的电流片等效为方形的[5]，如图3中阴影部分所示。那么，定子上的每一个线圈在定子内径处的电流密度都可由其等效成的方形的电流片的电流密度值Js所表示。

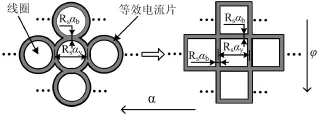
图3 等效电流片模型Fig.3 The model of equivalent current sheet

本文以永磁球形电动机的自转为例来分析电机的永磁体涡流损耗，方法同样适用于其他形式的运动。将永磁球形电动机沿赤道一周的定子线圈分为三相（位于同一经度的三个线圈为同一相，且通电方式是一样的），采用典型的三相桥式电路对定子线圈进行供电来实现电机的自转。

以任意选取的位于赤道处一层的一个线圈A1为分析对象，分别沿α，φ方向进行剖分，可以得到两个剖面图4(a)与图4(b)，如图4所示。

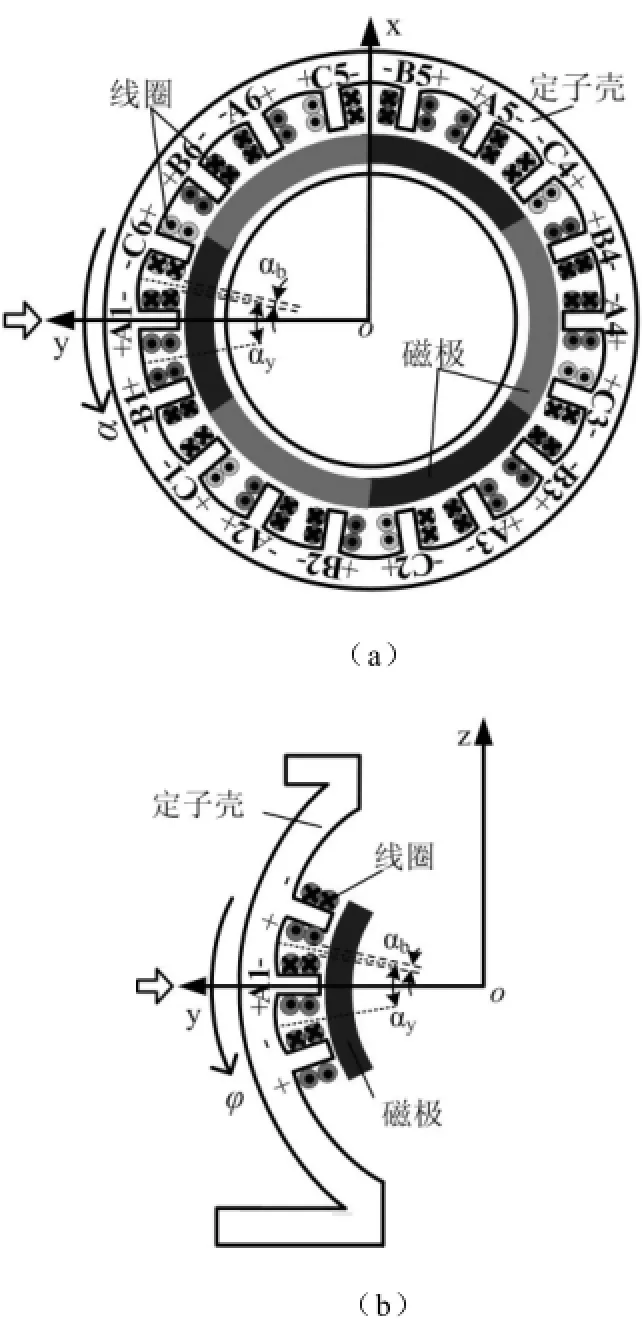
图4 永磁球形电动机的剖面图Fig.4 The cross sections of the PMSM

当仅有A相通电，电流为i时，电流密度的分布如图5所示。

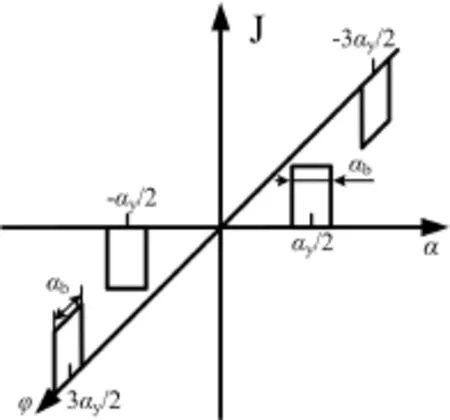
图5 等效电流片电流密度Fig.5 The current density of the equivalent current sheet

J的表达式可表示为

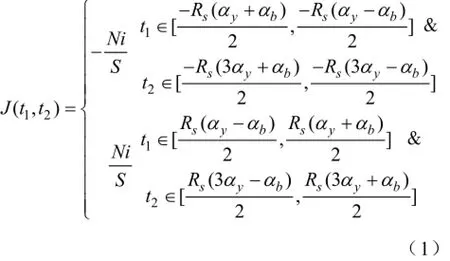
αy表示单个线圈所对应的机械角度，N为单个线圈总匝数，且方形电流片面积S为将J进行双重傅里叶分解，即:

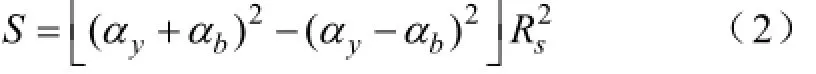
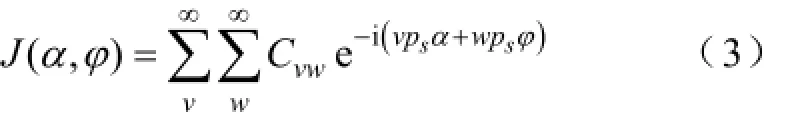
其中，v与w分别为沿α，φ方向的空间谐波次数，i为虚数单位，ps为定子极对数，且

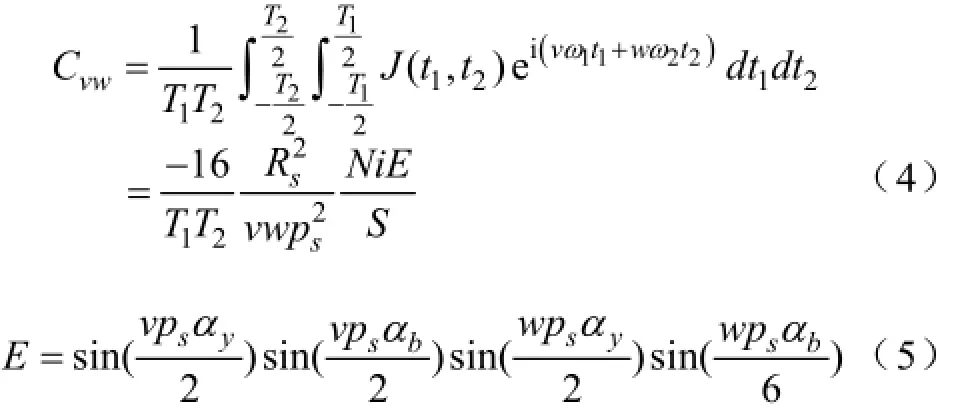
其中，T1与T2分别为对α，φ进行双重傅里叶分解的周期值，并引入ω1与ω2，分别为对应的角频率，且

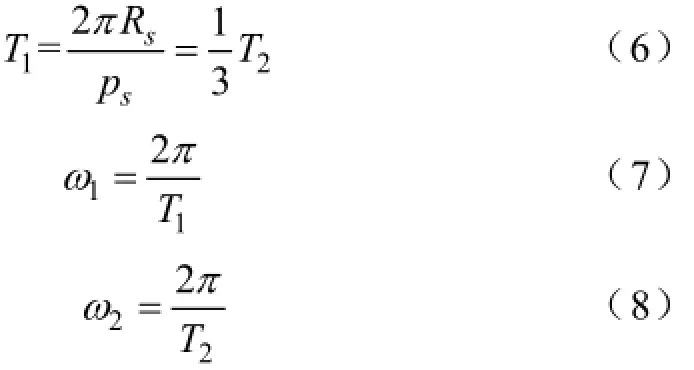
所以，综合式（3）与式（4），可推得

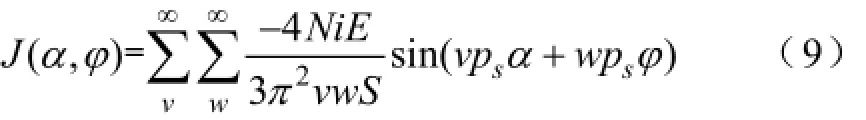
以上电流密度仅分析了A相通电时的情况，由球形电动机的通电方式可知，位于同一经度的三个线圈为同一相，因而不涉及三相电流叠加，只需将沿α方向的三相电流进行叠加。由于三相电流在空间与时间上对称，假定各次时间谐波次数为u，幅值为Iu，则A、B、C三相电流时间表达式为

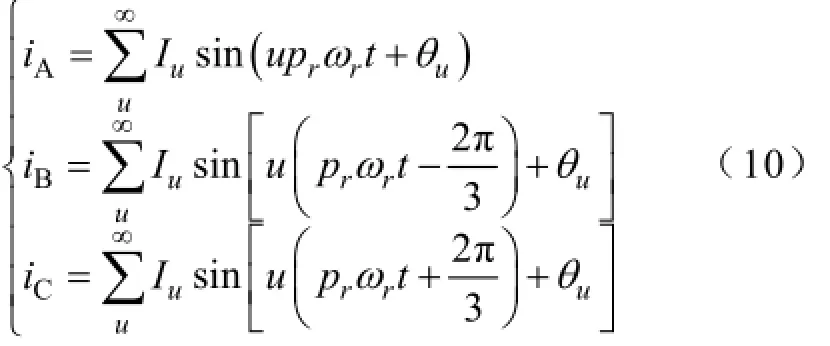
式中，ωr为转子角速度，θu为各次时间谐波相角，pr为转子极对数。

将式（10）代入式（9），可得三相电流密度傅里叶级数表达式

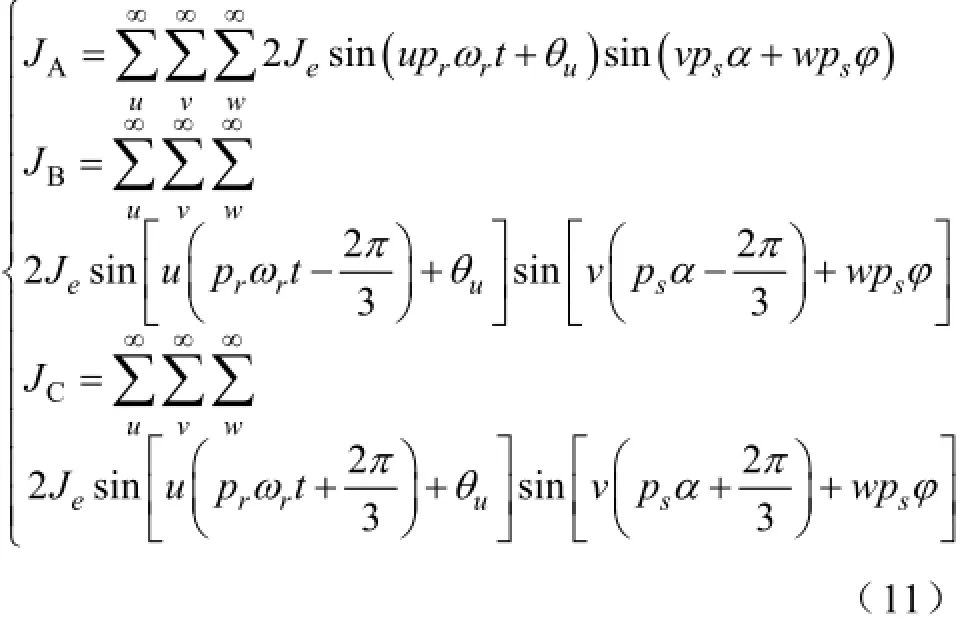
其中，

所以，位于定子内径处的等效电流片的电流密度分布表达式为

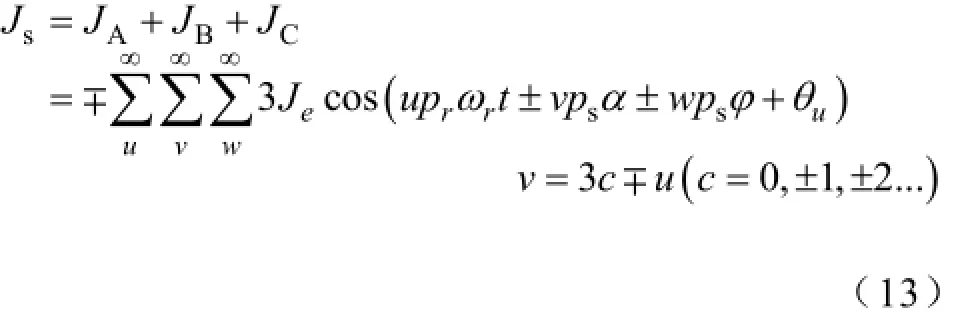
3 定子线圈电磁场分布

得到了定子线圈的电流密度分布，可以对线圈的电磁场分布进行分析。引入矢量磁位A，其在包含永磁体与气隙的三维求解域内满足三维拉普拉斯方程

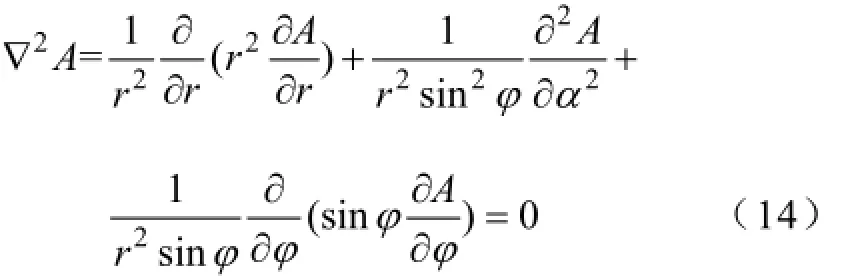
矢量磁位A在球坐标系下的通解为

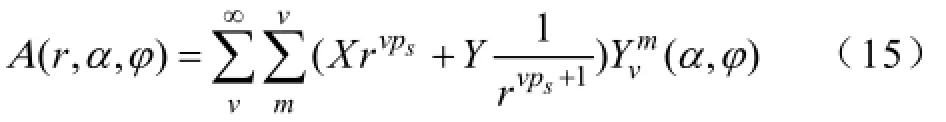
其中，X和Y为待定系数，且

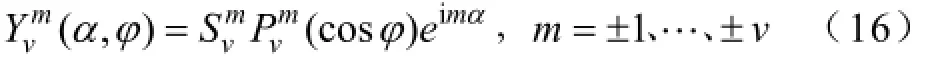
其中

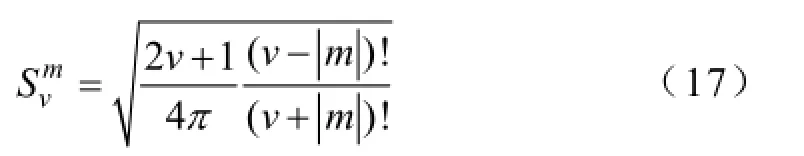
给定永磁球形电动机边界条件

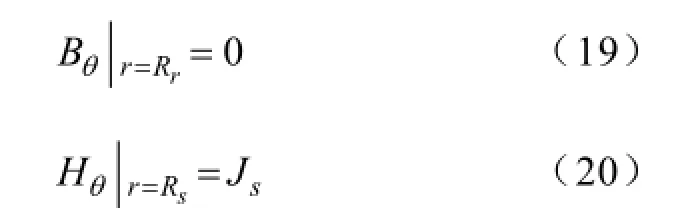
矢量磁位可解得

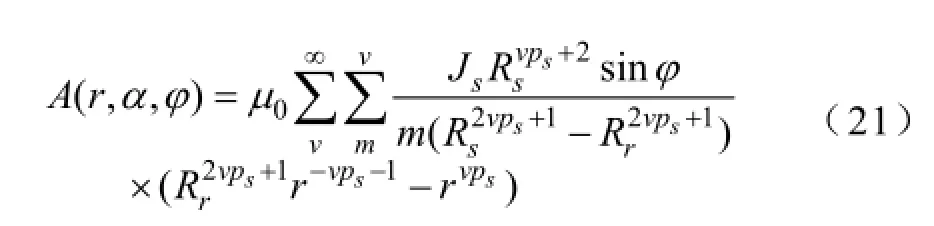
将式(13)代入上式，可得

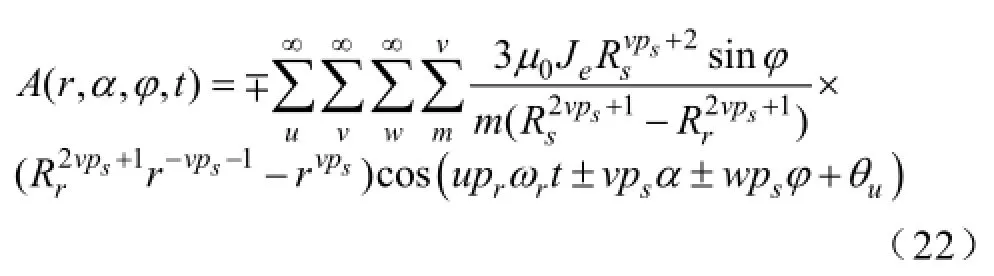
由此矢量磁位可以得到定子线圈电磁场的Br，Bθ和Bφ三个磁密分量，如图6所示。

图6 磁密分布Fig.6 The flux density distribution

由图6可知，三个分量的幅值相差不大，都在0.15特斯拉左右，永磁球形电动机的结构的特殊性使其较常规电机多了一个磁密分量Bφ，且其幅值较大，不容忽视，这也说明了对永磁球形电动机进行三维建模和分析的必要性。

4 永磁体涡流损耗计算

将式(22)在静止坐标系下的表示形式转换为旋转坐标系下的表示形式，有α=θ+ωrt ，所以

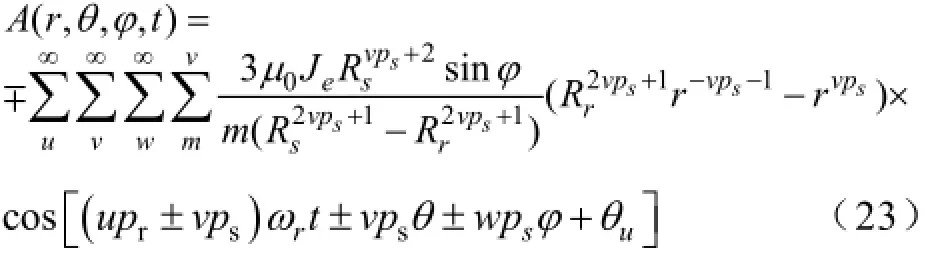
永磁体中由时变的定子线圈电磁场感应产生的涡流可以由下式表示

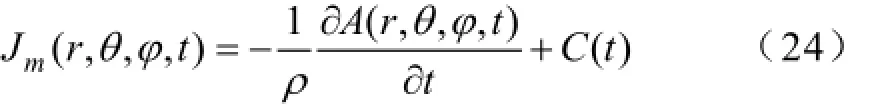
其中，ρ为永磁体的磁阻率，C(t) 的引入是因为每个磁极对外界总电流密度表现为零，所以永磁体内的感应电流需满足如下约束条件

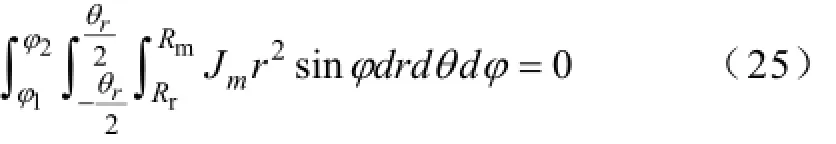
其中，φ1、φ2为磁极上下边缘处的纬度。永磁球形电动机的永磁体涡流损耗为

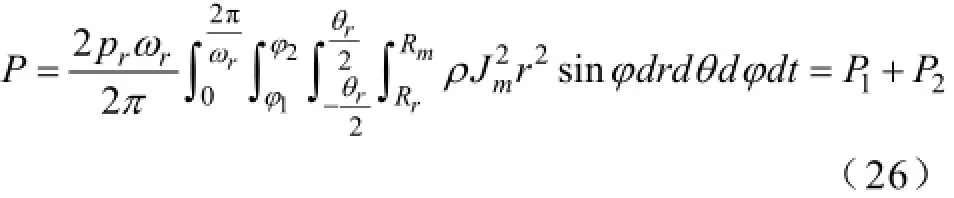
令φr=φ2-φ1，P1、P2分别为

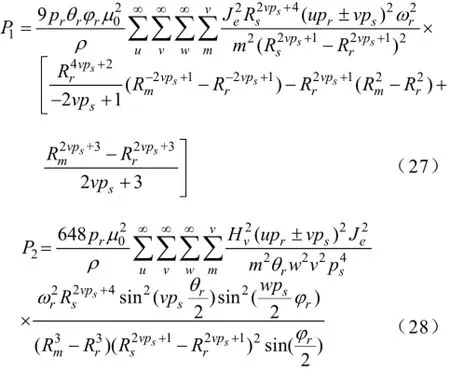
其中，

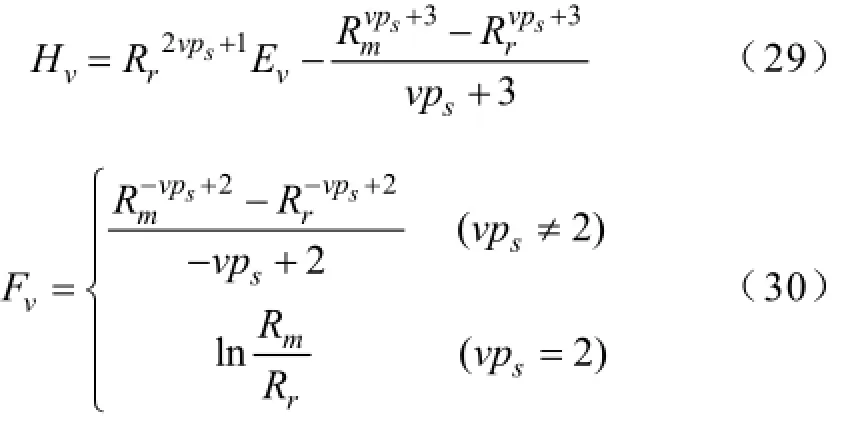
5 永磁体涡流损耗分析

涡流损耗的计算需要应用到相电流各次时间谐波的幅值Iu，可以应用有限元法得到相电流波形。电机的相关参数如表2所示。永磁球形电动机空载转速为45rpm时，有限元法得到的A相的相电流波形图如图7所示。

表2 结构和材料参数Tab.2 Structure and material parameters

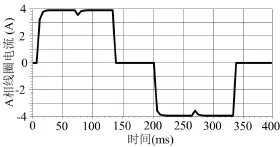
图7 A相电流波形Fig.7 The current waveform of phase A

可以看出，电流波形为非正弦，含有谐波分量。对此波形进谐波分析就可以得到各次时间谐波的幅值Iu与相位θu，可以将此结果应用到解析模型。其中各次谐波的幅值如图8所示。

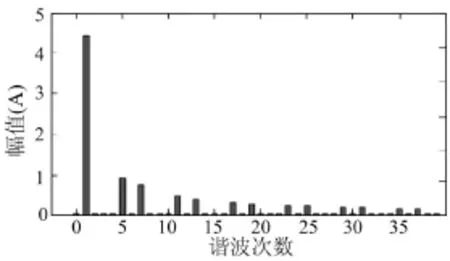
图8 电流谐波Fig.8 The current harmonics

可以看出，除基波外， 5、7、11、13次谐波的幅值还是比较高的，随着转速的增加，它们在电机不同部位产生的损耗将会很高。

由式(26)可以得到永磁球形电动机永磁体涡流损耗随不同参数变化的三维图形，如图9所示。其中，转速为300rpm，相电流为10A，空载。

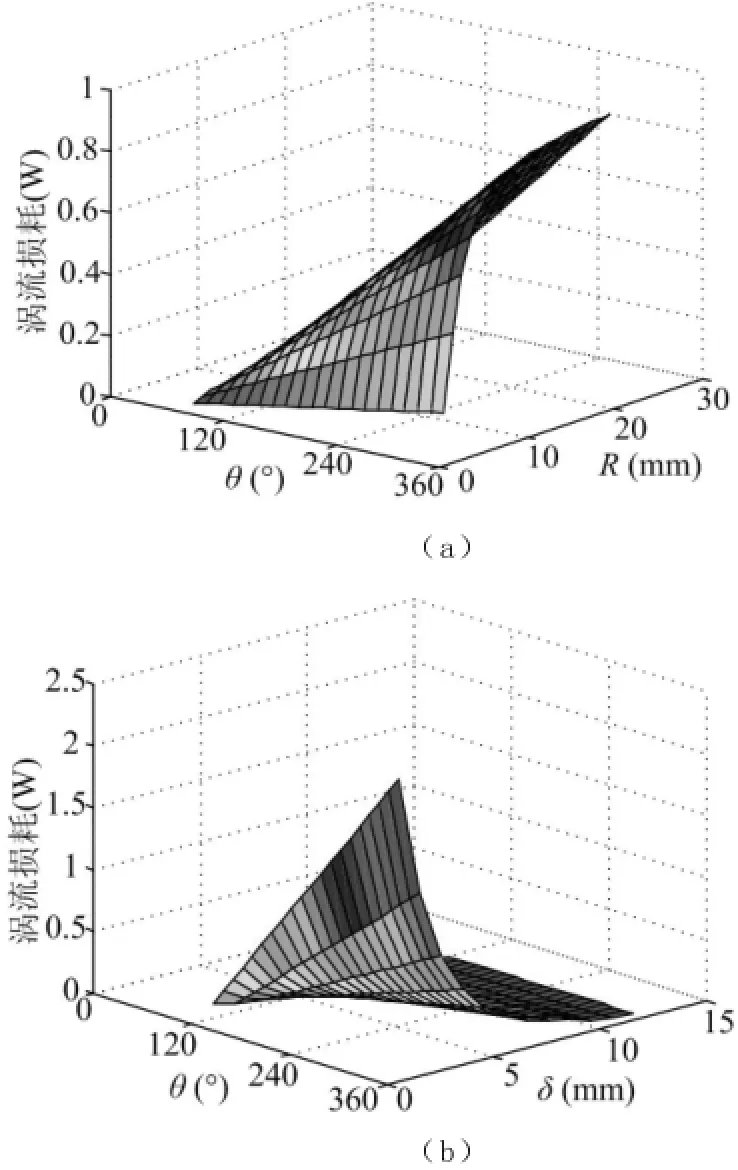
图9 永磁体涡流损耗随不同参数变化的三维图形Fig.9 The influence of different parameters on eddy current loss 3-D diagram

图9 a给出了永磁体涡流损耗随永磁体经度角θ和永磁体厚度R的变化情况。图9b给出了永磁体涡流损耗随永磁体经度角θ和气隙长度δ的变化情况。为了便于分析，图10给出了当永磁体经度角θ为360°时的二维图形，图10a给出了R对涡流损耗的影响，图10b给出了δ对涡流损耗的影响。

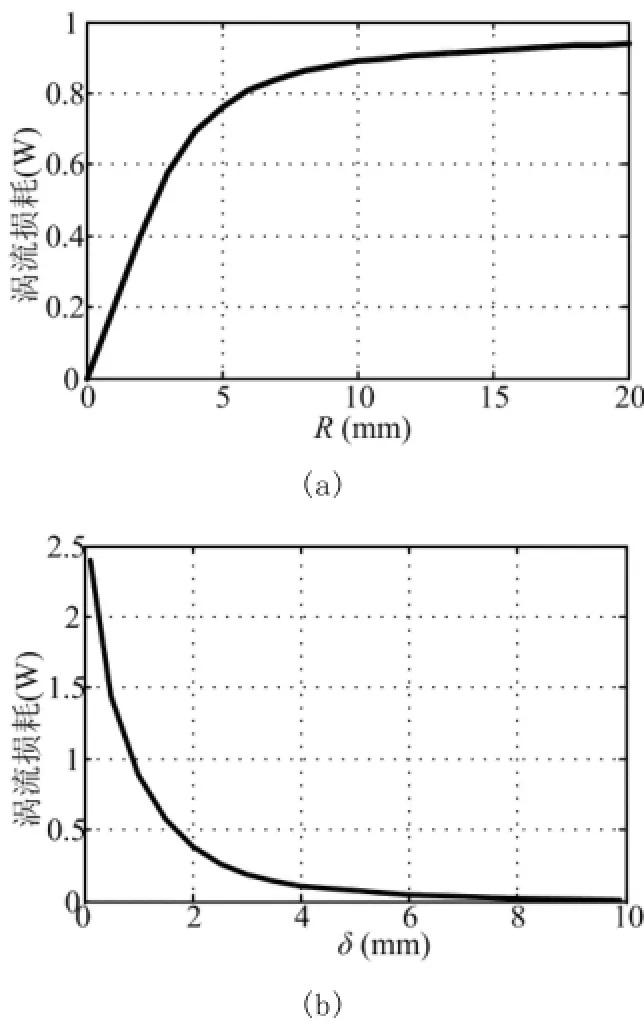
图10 θ为360°时不同参数对涡流损耗影响的二维图Fig.10 The influence of different parameters on eddy current loss2-D diagram when θ is 360°

由图10a可以看出，永磁体内的涡流损耗随着永磁体厚度的增大而增大。当永磁体太厚时，交变的磁场在永磁体内衰减较快，因而出现了图中所示的永磁体大于10mm后涡流损耗几乎不再增加的情况。永磁体太厚也会增加转子重量，提高成本，降低工作性能，所以应该减小永磁体厚度，但是不能太薄，否则会严重削弱永磁体的磁密分布[4]。适当地减小永磁体厚度（不大于10mm），将减少永磁体运动时产生的涡流损耗，并且提高电动机的工作性能。

由图10(b)可以看出，随着气隙逐渐增大，涡流损耗迅速下降。这是由于气隙的增大会使谐波磁动势在气隙处的降落增大，从而使永磁体遭受的磁动势降低，进而减少了涡流损耗。但气隙不能过大，否则会降低输出转矩。因此，在不影响电机运行的前提下，适量增加气隙长度（不小于1mm）将会大大降低永磁体涡流损耗，减少永磁体的发热，延长电机的寿命。

6 有限元仿真验证

对于永磁体涡流损耗，可以应用三维有限元法得到的涡流密度分布J直接计算得到[16]，计算公式为

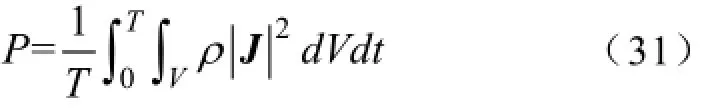
图11为永磁球形电动机不同转速时的磁极内涡流密度分布的有限元仿真结果。

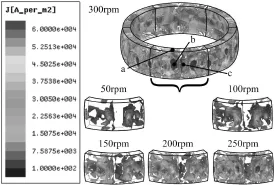
图11 涡流密度分布图Fig.11 The eddy current density distribution

为了分析磁极不同区域涡流密度分布情况，分别对a、b和c三个点进行作图，其中，a点位于非赤道一层的线圈所对应的区域，b点位于赤道一层的线圈所对应的区域，c点位于赤道一层的两个相邻的线圈所夹空隙对应的区域，随转速的不同，各点处涡流密度变化曲线如图12所示。

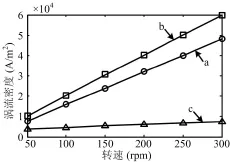
图12 涡流密度对比Fig.12 The comparison of eddy current density

由图12可以看出，相比之下，c点所处区域的涡流密度数值很小，而b点所处区域的涡流密度明显大于其他区域，这与永磁球形电动机的定子线圈的分布情况有关，多个线圈的相互独立的排列形式造成了永磁体内涡流密度的不均匀分布。

将本文提出的永磁体涡流损耗三维解析模型与有限元法所得结果进行比较，如图13所示。

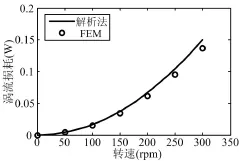
图13 电机不同转速下单块磁极涡流损耗Fig.13 The eddy current loss of a single pole at different speeds

可以看出两者结果基本吻合，验证了此解析模型的有效性。

7 实验

永磁球形电动机的实验平台如图14所示。该实验平台采用三相桥式电路对永磁球形电动机定子线圈供电，实现了永磁球形电动机的连续自转运动。空载实验时，当电动机转速为45rpm时，A相电流波形如图15所示。图中，纵轴坐标对应2A/div。

图14 永磁球形电动机实验平台Fig.14 The experiment platform of the PMSM

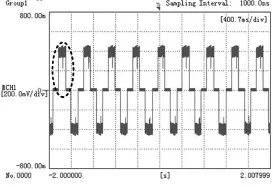
图15 A相电流波形图Fig.15 The current waveform of phase A

虚线部分的放大图为图16，纵轴坐标对应2A/div，可以看出，空载时，通过定子线圈的电流为4A，该实验波形与有限元仿真波形图7相吻合。

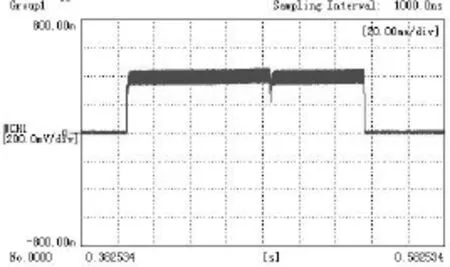
图16 局部放大图Fig.16 The partial enlarged diagram

8 结论

本文采用双重傅里叶级数法得到了永磁球形电动机定子线圈的等效电流片模型，基于矢量磁位,建立了永磁体涡流损耗解析模型，得到了等效电流片的磁密分布，并求解出永磁体涡流损耗的三维解析表达式，该表达式考虑到了空间谐波与时间谐波对永磁体涡流损耗的影响。分析了不同永磁体厚度与气隙等结构参数情况下永磁体产生的涡流损耗。通过有限元仿真，验证了该解析法的准确性。本文的解析模型对永磁球形电动机的初始设计与优化具有一定的借鉴意义。

附录 A

式（13）的推导过程如下，

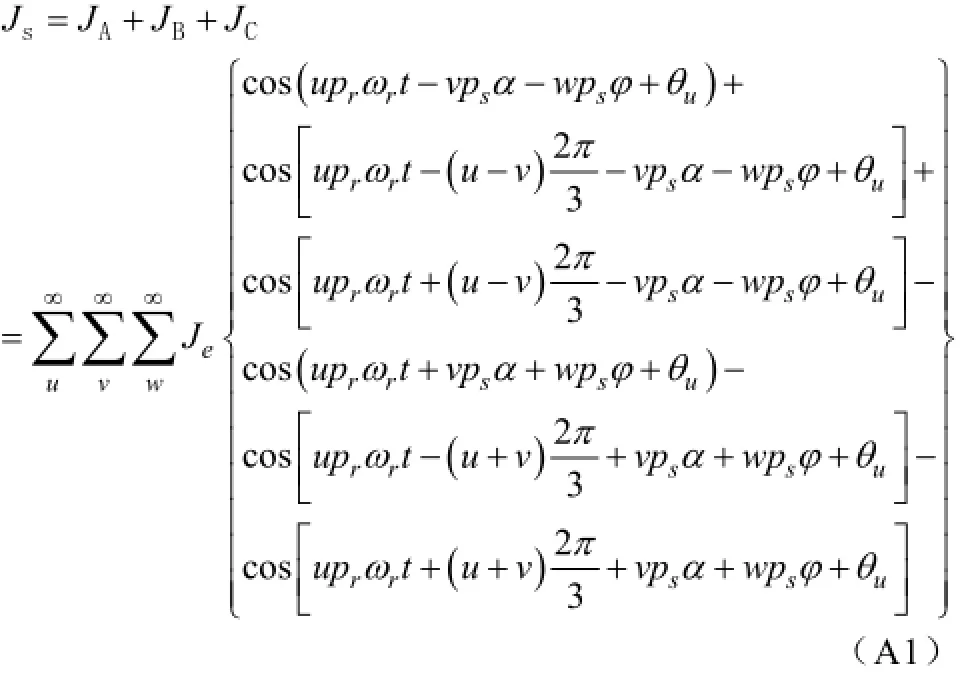
当v=3c-u（c =0,±1,±2...）时，有

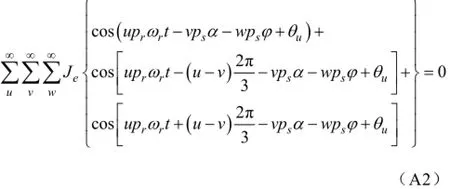
所以，

当v=3c+u（c =0,±1,±2...）时，有

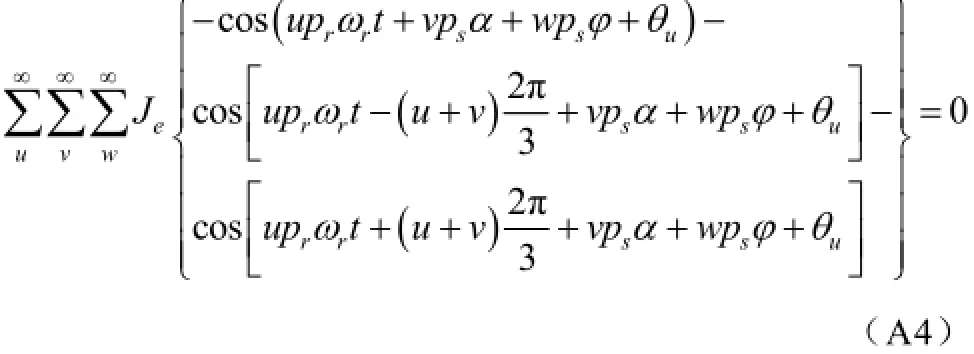
所以，

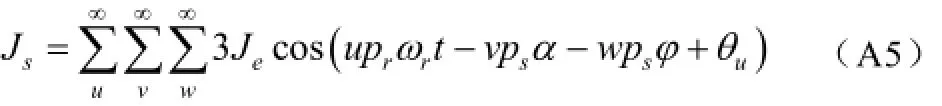
综上，

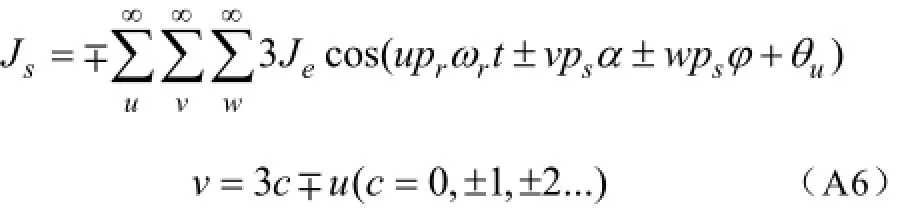
附录 B

电枢反应磁场的Br，Bθ和Bφ三个磁密分量，

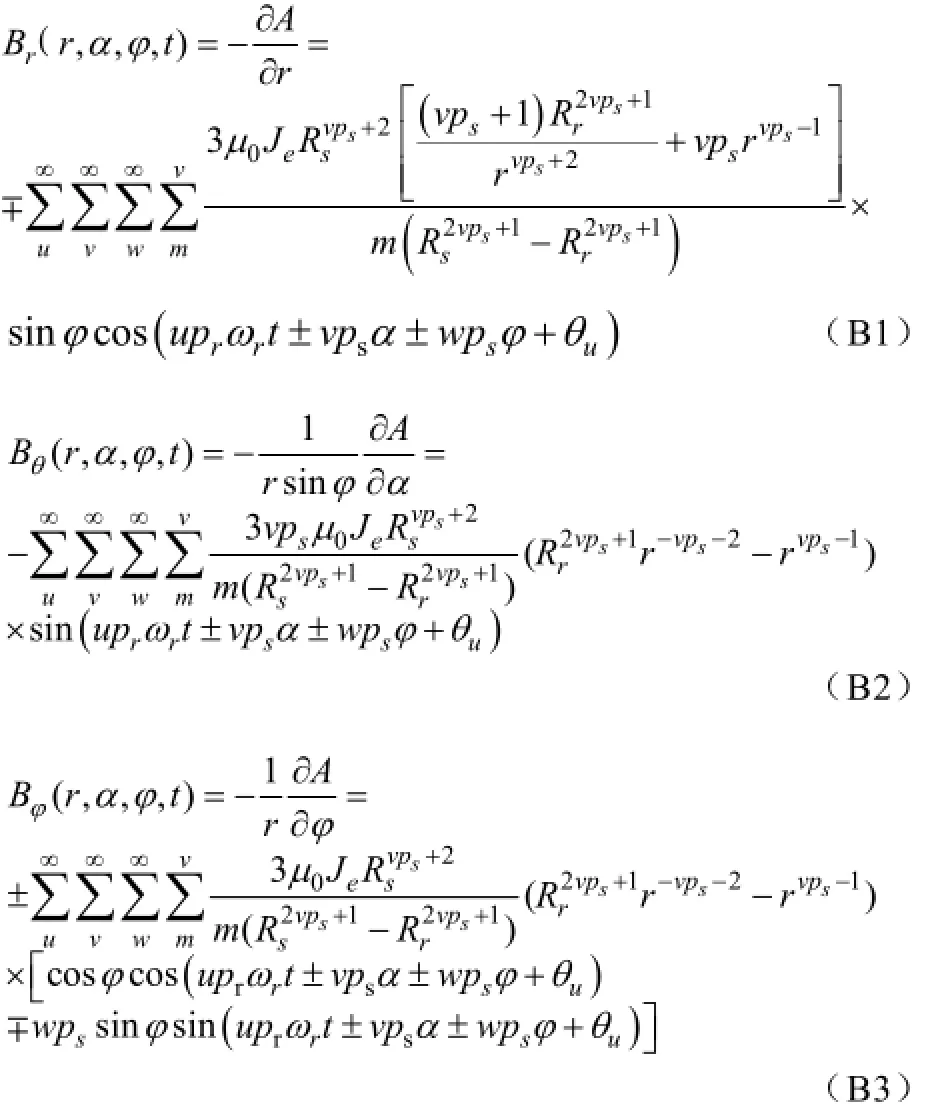
[1] Li H F, Xia C L, Shi T N. Spherical Harmonic Analysis of a Novel Halbach Array PM Spherical Motor[C]. IEEE International Conference on Robotics and Biomimetics, 2007： 2085-2089.

[2] Xia C L, Li H F, Shi T N. 3-D Magnetic Field and Torque Analysis of a Novel Halbach Array Permanent-Magnet Spherical Motor[J]. IEEE Transactions on Magnetics, 2008, 44(8)： 2016-2020.

[3] Li H F, Xia C L, Song P, et al. Magnetic Field Analysis of A Halbach Array PM Spherical Motor[C]. IEEE International Conference on Automation and Logistics, 2007： 2019-2023.

[4] 李洪凤. Halbach阵列永磁球形电动机三维磁场分析[D]. 天津： 天津大学, 2008.

Li H F. 3-D Magnetic Field Analysis of a Halbach Array PM Spherical Motor[D]. Tianjin： Tianjin University, 2008.

[5] Xia C L, Song P, Li H F, Li B and Shi T N. Research on Torque Calculation Method of Permanent-magnet Spherical Motor Based on the Finite-Element Method[J]. IEEE Transactions on Magnetics. 2009, 45(4)： 2015-2022.

[6] Yan L, Chen I M, Lee K M, et al. Modeling and Iron-Effect Analysis on Magnetic Field and Torque Output of Electromagnetic Spherical Actuators With Iron Stator, IEEE/ASME Transactions on Mechatronics[J], 2012, 17 (6)： 1080-1087.

[7] Xin J G, XIA C L, Li H F, Shi T N. A novel orientation measurement using optical sensor for spherical motor[J]. Science China, 2013, 56 (6)：1330-1339.

[8] 信建国, 夏长亮, 李洪凤, 史婷娜. 基于解析模型的永磁球形电机永磁体优化设计[J]. 电工技术学报, 2013, 28(7)： 87-95.

Xin Jianguo, Xia Changliang, Li Hongfeng, Shi Tingna. Optimization design of permanent magnet array for spherical motor based on analytical model[J]. Transactions of China Electrotechnical Society, 2013, 28(7)： 87-95.

[9] 鞠鲁峰, 王群京, 李国丽. 永磁球形电机的支持向量机模型的参数寻优[J]. 电工技术学报, 2014, 29(1)： 85-90.

Ju Lufeng, Wang Qunjing, Li Guoli. Parameter optimization for support vector machine model of permanent magnet spherical motors[J]. Transactions of China Electrotechnical Society, 2014, 29(1)： 85-90.

[10] Zhu Z Q, Howe D. Eddy-Current Loss in the Rotor Magnets of Permanent-Magnet Brushless Machines Having a Fractional Number of Slots Per Pole[J]. IEEE Transactions on Magnetics, 2005, 41(9)：2462-2469.

[11] Norio Takahashi, Hirofumi Shinagawa, Daisuke Miyagi. Analysis of Eddy Current Losses of Segmented Nd-Fe-B Sintered Magnets Considering Contact Resistance[J]. IEEE Transactions on Magnetics, 2009, 45(3)： 1234-1237.

[12] Seok-Myeong Jang, Hyun-Kyu Kim, Jang-Young Choi. Analysis and comparison for rotor eddy current losses of permanent magnet synchronous generator according to dc and ac load conditions[C]. Journal of applied physics, 2009： 300-303.

[13] Nannan Zhao, Z. Q. Zhu, Weiguo Liu. Rotor Eddy Current Loss Calculation and Thermal Analysis of Permanent Magnet Motor and Generator[J]. IEEE Transactions on Magnetics, 2011, 47(10)： 4199-4202.

[14] 李伟力, 孙佳慧, 孙红丽. 汽轮发电机稳态与负序工况下转子涡流损耗计算和温度场分析[J]. 电工技术学报, 2012, 27(9)： 174-182.

Li Weili, Sun Jiahui, Sun Hongli. Calculation and analysis of eddy loss and temperature field in rotor of synchronous generator under steady state and negative sequence[J]. Transactions of China Electrotechnical Society, 2012, 27(9)： 174-182.

[15] 解恩, 刘卫国, 罗玲, 王璞. PWM 调制对无刷直流电机转子涡流损耗的影响[J]. 电工技术学报, 2013, 28(2)： 117-125.

Xie En, Liu Weiguo, Luo Ling, Wang Pu. Influence of PWM on rotor eddy-current losses in brushless DC motor[J]. Transactions of China Electrotechnical Society, 2013, 28(2)： 117-125.

[16] H. Domeki, Y. Ishihara, C. Kaido, Y. Kawase, S. Kitamura, T. Shimomura, N. Takahashi, T. Yamada, and K. Yamazaki. Investigation of benchmark model for estimating iron loss in rotating machine[J]. IEEE Trans. on Magn., 2004, 40(2)： 794-797.

Eddy Current Loss Analysis in the Rotor magnets of Permanent Magnet Spherical Motor

Li Hongfeng Shen Yanbo
（School of Electrical Engineering and Automation Tianjin University Tianjin 300072 China）

The rotor magnets of the permanent magnet spherical motor(PMSM) have a structure of spherical cone, and all of the stator coils are distributed on the inner surface of the stator shell independently of each other. In view of these characteristics, a three-dimensional(3-D) analytical model is presented to study the eddy current loss of magnets in the PMSM. And this model combines the double Fourier series decomposition and the magnetic vector potential method. First, the current density distribution at the inner diameter of the stator is described by employing the double Fourier series decomposition. With the current density distribution and other boundary conditions, the unique solution of magnetic vector potential is obtained by solving 3-D Laplace’s equations. Further, the analytic expression of PM eddy current loss in the PMSM is derived. This model considers the effect of harmonics, and the influence of different motor parameters on the eddy current loss has been analyzed. The results of analytical method and finite element method(FEM) are compared, proving the effectiveness of the proposed analytical model.

PMSM, double Fourier series decomposition, magnetic vector potential method, analytical model of PM eddy current loss

TM351

李洪凤 女，1979年生，副教授，研究方向为电机与电器。

国家自然科学基金（51007061）。

2014-07-10

沈彦波 男，1991年生，硕士，研究方向为电机与电器。