岩石钻孔爆破粉碎区计算模型的改进
冷振东,卢文波,陈 明,严 鹏,胡英国
(1.武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072; 2.武汉大学水工岩石力学教育部重点实验室,湖北 武汉 430072)
岩石钻孔爆破粉碎区计算模型的改进
冷振东1,2,卢文波1,2,陈 明1,2,严 鹏1,2,胡英国1,2
(1.武汉大学水资源与水电工程科学国家重点实验室,湖北 武汉 430072; 2.武汉大学水工岩石力学教育部重点实验室,湖北 武汉 430072)
为了研究炮孔周围岩石的破坏机理,准确预测粉碎区的范围,提出了一种计算钻孔爆破粉碎区范围的改进模型。该四分区模型考虑了破裂区内侧的环向压应力和炮孔空腔膨胀的影响,假定粉碎区为丧失了内聚力但仍具有内摩擦力的散体介质。采用弹塑性力学理论推导了柱状装药起爆条件下的岩石钻孔爆破粉碎区半径公式。计算结果表明,岩石钻孔爆破粉碎区范围通常为1.2~5.0倍炮孔半径,不同种类岩石的粉碎区范围差别很大。与其他计算模型相比,本模型的计算结果与实验数据更吻合。
爆炸力学;计算模型;环向应力;粉碎区;改进;空腔膨胀
近十年来,随着现代化矿山的建设和西部水电的开发,钻孔爆破作为石方开挖的最常用技术得到了快速发展。大量的研究资料表明,炸药破碎岩石的能量仅占炸药总能量的20%~30%。N.V.Melnikov[1]指出,在传统装药结构的爆破中,有不少于50%的爆炸能量浪费在粉碎圈和破裂圈内侧部分的过度破碎上,而且极度粉碎的岩石很容易堵塞破裂区形成的裂纹通道,阻碍爆炸气体向裂纹中的进一步扩散,影响了气体的“气楔”作用[2],减少了岩石的破坏范围。同时,在粉碎区内比表面积大的颗粒会吸收爆生气体的大量热能,降低了炸药能量的有效利用率。因此,如何控制岩石的爆破粉碎区范围对于提高炸药能量的有效利用率、降低炸药单耗和工程成本具有重要意义。
对岩石在炸药作用下的破坏范围已有较深入的研究[3~6]。目前粉碎区计算模型的结果差异很大,主要有以下几种:G.Szuladzinski[7]模型假设炮孔周围的岩石为弹性体,粗略地假定炸药的有效能量为炸药爆热的三分之二,不能反映装药结构对粉碎区范围的影响;N.Djordjevic[8]基于Griffith强度准则的计算模型只适用于脆性岩石;A.A.Il’yushin[9]基于Mohr-Coulumb准则的计算模型认为粉碎区岩石仍具有黏聚力,但是A.Vovk等[10]在石灰岩和混凝土中的爆破实验结果表明,Il’yushin模型的结果偏大。另一方面Il’yushin公式的推导过程中,将爆腔膨胀过程中的气体绝热指数取为常数,因此该公式不适用于不耦合系数较大的情况,从而使公式具有很大的局限性。S.S.Kanchibotla等[11]和S.Esen等[12]基于工程经验和实验统计的计算公式简单,但是结果离散性较大;国内学者戴俊[13]基于Mises屈服准则的计算模型等。由于炮孔空腔的膨胀,作用在炮孔上的压力会降低[14],上述模型除Il’yushin外均未考虑炮孔空腔膨胀对炮孔压力的影响。
本文中提出一种计算钻孔爆破粉碎区范围的改进模型,由于破裂区是连接粉碎区和弹性区的约束,此区域不可能被径向裂纹完全破坏,因此将破裂区划分为两部分,内侧部分(破裂Ⅰ区)的介质为塑性破坏,环向压应力不为零;外侧部分(破裂Ⅱ区)介质受到径向裂缝破坏,丧失了环向承载力。假定粉碎区为丧失了黏聚力的散体介质,但是破碎颗粒之间仍然具有内摩擦力。在此基础上,考虑炮孔空腔膨胀对炮孔压力降低的影响,推导柱状装药起爆条件下的岩石钻孔爆破粉碎区半径公式。
1 爆破破坏分布及计算条件
1.1 爆破破坏分布
炸药爆炸后,炮孔由里往外岩石依次承受剧烈的爆炸冲击波、应力波和地震波作用,岩石介质的连续性发生改变,呈现出不同的破碎和损伤状态。炮孔壁在向外扩展一定距离后逐渐稳定下来,最终形成膨胀空腔。根据周围岩石的破坏程度,炮孔周围的岩石可以划分为不同的区域,不同的学者对破坏分区的定义各不相同[15]。现有的计算模型通常把爆破作用的最终影响范围划分为粉碎区、径向开裂区和弹性变形区3部分,如图1(a)所示。
现有的模型[6-7,9]认为粉碎区和弹性区之间的整个区域被径向裂纹完全破坏,因而岩石只能传递径向应力,没有环向承载力,即σθ=0,从而简化物理过程。然而在实际过程中,破裂区是连接粉碎区和弹性区的约束,不可能造成径向完全的破坏,特别是破裂区的内侧部分岩石受到极高的径向压应力,由于泊松效应,必然会受到周围岩石的约束,因此环向压应力作用明显,不能忽略其作用。因此,我们把破裂区划分为2个部分,内侧部分(破裂Ⅰ区)的介质为塑性破坏,需要考虑环向应力的影响:σθ≠0;外侧部分(破裂Ⅱ区)介质受到径向裂缝破坏,丧失了环向承载力:σθ=0,改进模型能更好地反映炮孔周围岩石的实际破坏情况。
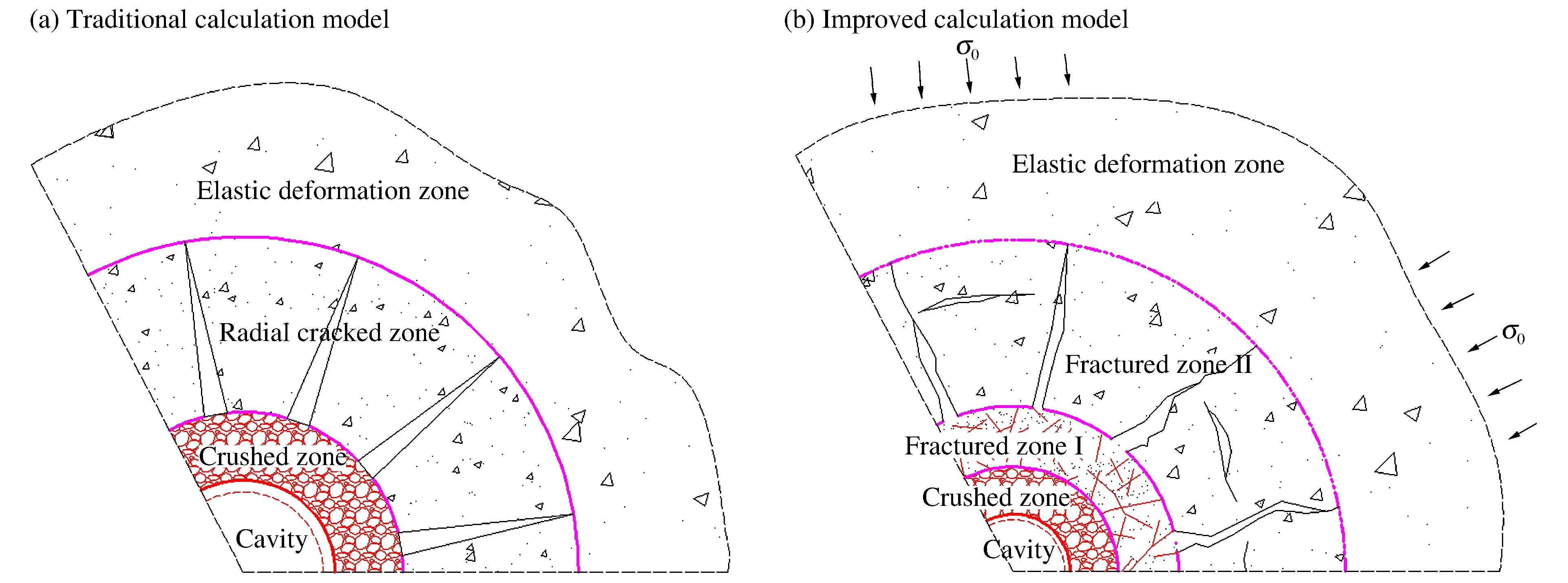
图1 传统模型和改进模型的岩石钻孔爆破破坏分区示意图Fig.1 Image of the damage zones surrounding a blasthole under blasting in traditional and improved calculation model
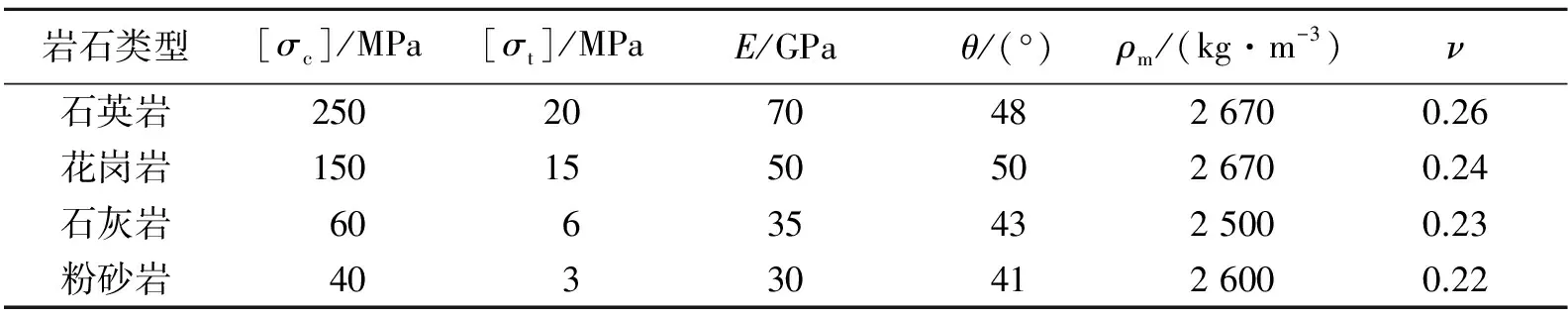
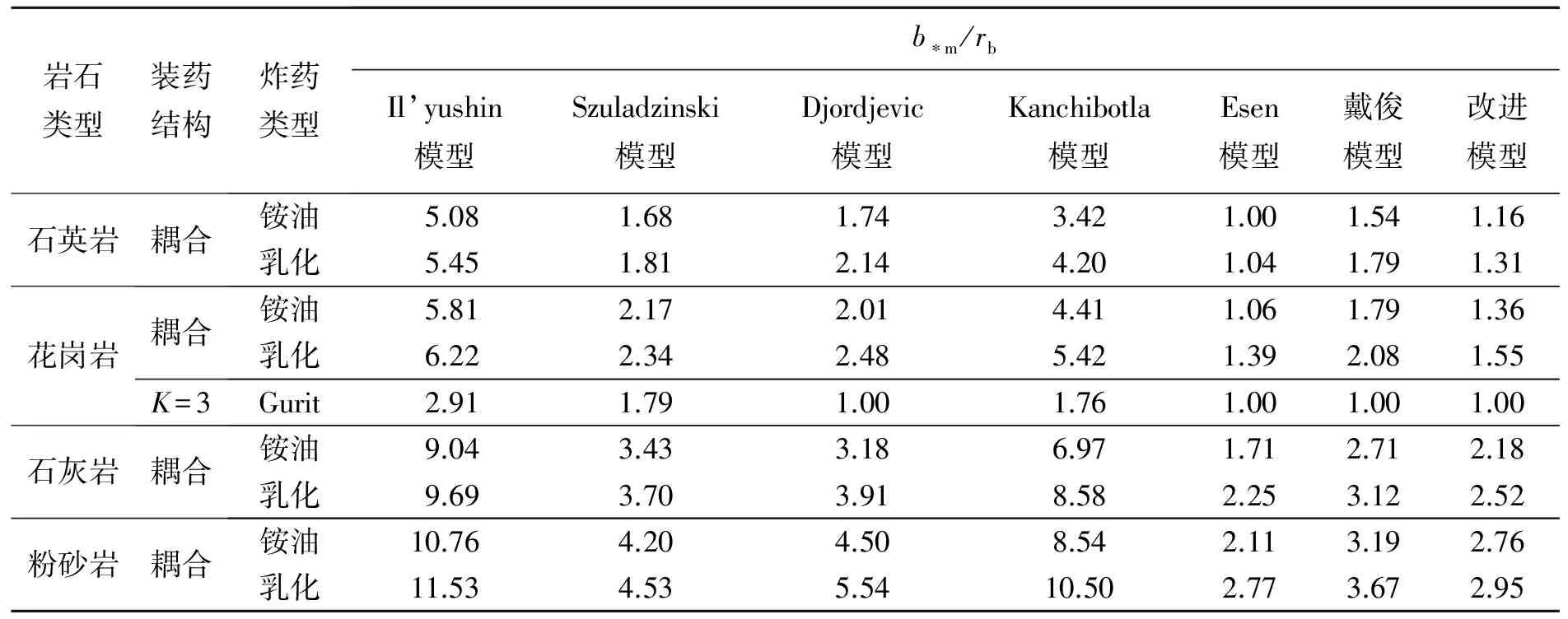
图1(b)为改进模型中的钻孔爆破破坏分区示意图,在该四分区模型中,各破坏分区的边界定义如下:粉碎区:a(t)≤r≤b*(t);破裂Ⅰ区:b*(t) 1.2 计算条件 在岩石介质中有一无限长的圆柱形空腔,受到一个内部沿轴向均布的爆炸荷载的作用,作如下假设:(1)圆柱形空腔沿轴向无限延伸,可将问题视为轴对称平面应变问题;(2)粉碎区岩石为各向同性、不可压缩且丧失黏聚力的散体介质,但是颗粒之间仍然具有内摩擦力;(3)爆生气体的膨胀过程为绝热膨胀,忽略进入岩石裂隙的爆生气体的体积。 2.1 弹性变形区 利用柱坐标系描述问题,在弹性区的应力分布为: (1) 式中:σr=bⅡ为弹性区的内边界(r=bⅡ)处的径向应力,σ0为岩石初始应力。在弹性变形区和破裂Ⅱ区的交界面上,环向应力达到岩石的抗拉强度:σθ=-[σt],故由式(1)得σr=bⅡ=[σt]+2σ0。 弹性区的位移 (2) 2.2 破裂Ⅱ区 破裂Ⅱ区的特征是介质受到裂缝破坏,丧失了环向承载力,但是径向仍为弹性,类似于径向柱杆,主要把破裂Ⅰ区传来的压力过渡到弹性区介质中去。破裂Ⅱ区满足σθ=0,平衡微分方程可以简化为: (3) 在破裂Ⅱ区外边界上有σr=[σt]+2σ0,内边界上有σr=[σc],其中[σc]为岩石单轴抗压强度。 由此得到破裂Ⅱ区的径向应力 (4) (5) 2.3 破裂Ⅰ区 破裂Ⅰ区为塑性破坏区,在破裂Ⅰ区产生大量裂缝,导致介质体积的膨胀,因此需要考虑该区域岩石的剪胀作用。采用非关联流动法则来描述破裂Ⅰ区岩石的剪胀特性: (6) 式中:h为破裂Ⅰ区岩石的剪胀率。 可以求得破裂Ⅰ区的位移 (7) 把Mohr-Coulomb屈服准则代入平衡微分方程得到破裂Ⅰ区径向应力的分布: (8) 2.4 粉碎区 在高温高压的爆炸气体的作用下,装药附近的岩石受到强烈的压缩剪切作用,结构被完全破坏,形成紧挨着空腔壁的粉末化区域。该区域的岩石可以视为各向同性、不可压缩并且没有粘聚力的散体介质,但是破碎颗粒之间仍然具有内摩擦力。在粉碎区采用没有凝聚内成分的Mohr-Coulomb强度准则: (9) 将(9)式代入平衡微分方程中解得粉碎区的径向应力 (10) 由粉碎区的不可压缩条件,解得粉碎区的位移 (11) u(t)对b*(t)求导得 (12) 则在膨胀空腔的壁面(r=a(t))上有 (13) 在初始时刻(t=0时),粉碎区由膨胀空腔壁面开始产生,此时有a=b*=rb,其中rb为炮孔半径。 对方程(13)两边积分,整理得 (14) 式中:b*m为粉碎区的最大半径,am为膨胀空腔的最大半径。 (15) 在膨胀空腔的后续扩展中,炮孔压力可以由两阶段的Jonse-Miller绝热方程来确定[18]: (16) 在r=am处,有σr=pm,即 (17) 联立(15)~(17)得 (18) 由式(18)即可求得最大膨胀空腔半径与炮孔半径的比值(am/rb),带入式(15)可求得粉碎区的范围(b*m/rb)。 (19) 联立方程(16)~(17)、(19)可得柱状装药起爆条件下的粉碎区半径公式: (20) 由公式(20)可以看出,粉碎区半径主要受以下因素的影响:(1)岩石特性,包括动抗压强度[σc]、动抗拉强度[σt]、弹性模量E、泊松比ν、剪胀特性h和初始应力σ0;(2)炮孔压力pb,炮孔压力pb又与炸药的密度ρ0、爆轰速度D以及装药结构有关;(3)炮孔半径rb。 表1给出了计算中采用的4种岩石的物理力学参数,炸药分别采用铵油炸药(ρ0=0.9 g/cm3,D=3 600 m/s)、乳化炸药(ρ0=1.05 g/cm3,D=4 100 m/s)和Gurit炸药(ρ0=1.0 g/cm3,D=2 200 m/s)。 表1 各种岩石的物理力学参数 表2中列出了各种计算模型在不同岩石不同炸药类型条件下的粉碎区范围。同种岩石采用相同的装药结构时,铵油炸药产生的粉碎区比乳化炸药的小。当炮孔压力值一定时,不同种类的岩石的粉碎区范围差别很大,对于强度较大的硬岩,粉碎区半径不到2倍炮孔半径;而对于强度较小的软岩,粉碎区半径可达3~5倍甚至更大的炮孔半径。绝大多数学者认为在工程爆破中粉碎区的半径不会超过3~5倍炮孔半径[18],这与本文的计算相符合。本文中列举的4种岩石的计算结果表明,各种计算模型得到的粉碎区的范围差别较大,本文计算结果与S.Esen和戴俊的结果较为接近,介于两者之间。Il’yushin以及Kanchibotla的计算结果最大,引起这种显著差异的原因之一是各种模型对于粉碎区的定义不同,Il’yushin和Kanchibotla模型认为发生过塑性破坏、裂隙网状分布的破裂Ⅰ区也属于粉碎区。 表2 不同粉碎区范围计算模型的计算结果对比 注:K为径向不耦合系数,K=炮孔直径装药直径。 图2 不同计算模型的粉碎区计算结果b*m和实验数据*m对比Fig.2 Comparison of different models with full scale blasting experiments M.Olsson等[19]通过在花岗岩中的不耦合装药钻孔爆破实验来测量粉碎区的范围,采用直径64 mm的炮孔和直径22 mm的Gurit炸药。实验发现炮孔周围几乎观察不到粉碎区。由表2中不耦合装药一栏的计算结果可知,Il’yushin、Szuladzinski和Kanchibotla这3种模型的粉碎区半径和炮孔半径的比值b*m/rb分别为2.91、1.79、1.76,而本文计算结果为1.00,即几乎不会产生粉碎区,与实验结果很吻合。其中,由于Szuladzinski公式中的粉碎区范围只与炸药密度、单位质量炸药释放的热量及岩石抗压强度有关,不适用于不耦合装药结构的情况;Il’yushin和Kanchibotla这2种模型在不耦合装药结构时的计算结果误差较大,Djordjevic、S.Esen、戴俊和本文的改进模型可以有效反映不耦合装药对粉碎区半径的影响。 提出了一种计算钻孔爆破粉碎区范围的改进模型,认为破裂区内侧部分环向应力不为零,考虑了炮孔空腔膨胀对炮孔压力降低的影响,推导了柱状装药起爆条件下的岩石钻孔爆破粉碎区半径公式,并与实验数据进行了对比,主要有以下结论:(1)破裂Ⅰ区环向应力的非零假定(σθ≠0)使改进模型更能反映炮孔周围岩石的实际受力情况。与其他计算模型相比,改进模型能与实验数据更好地吻合。(2)基于改进模型推导的粉碎区半径公式可以反映岩石特性、炸药特性、装药结构及炮孔半径对粉碎区范围的综合影响。计算表明,不同种类岩石的粉碎区范围差别很大,通常粉碎区半径为1.2~5.0倍炮孔半径。 在实际岩石钻孔爆破中,岩石的破坏机理非常复杂,本文仅仅是在基于若干假设的前提下对该现象的讨论,对于岩石钻孔爆破的破坏分区机制还需要更进一步研究。 [1] Melnikov N V. Influence of explosive charge design on results of blasting[C]∥International Symposium on Mining Research. Clark G B. London, Pergamon, 1962:147-155. [2] 朱红兵,卢文波,吴亮.空气间隔装药爆破机理研究[J].岩土力学,2007,28(5):986-989. Zhu Hong-bing, Lu Wen-bo, Wu Liang. Research on mechanism of air-decking technique in bench blasting[J]. Chinese Journal of Rock and Soil Mechanics, 2007,28(5):986-989. [3] 王明洋,邓宏见,钱七虎.岩石中侵彻与爆炸作用的近区问题研究[J].岩石力学与工程学报,2005,24(16):2859-2863. Wang Ming-yang, Deng Hong-jian, Qian Qi-hu. Study on problems of near cavity of penetration and explosion in rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24(16):2859-2863. [4] Jimeno E L, Carcedo F J A. Drilling and blasting of rocks[M]. Taylor & Francis Group, 1995. [5] Ouchterlony F, Moser P. On the branching-merging mechanism during dynamic crack growth as a major source of fines in rock blasting[C]∥The 10th International Symposium on Rock Fragmentation by Blasting. New Delhi, India, 2012:65-75. [6] 钱七虎.岩石爆炸动力学的若干进展[J].岩石力学与工程学报,2009,28(10):1945-1968. Qian Qi-hu. Some advances in rock blasting dynamics[J]. Chinese Journal of Rock Mechanics and Engineering, 2009,28(10):1945-1968. [7] Szuladzinski G. Response of rock medium to explosive borehole pressure[C]∥Proceedings of the Fourth International Symposium on Rock Fragmentation by Blasting-Fragblast-4. Vienna, Austria, 1993:17-23. [8] Djordjevic N. A two-component of blast fragmentation[C]∥Proceedings of the Sixth International Symposium on Rock Fragmentation by Blasting-Fragblast. Johannesburg, South Africa, 1999:213-222. [9] Hustrulid W A. Blasting principles for open pit mining-Theoretical foundations[M]. Rotterdam: Balkema, 1999. [10] Vovk A A, Mikhalyuk A V, Belinskii I V. Development of fracture zones in rocks during camouflet blasting[J]. Journal of Mining Science, 1973,9(4):383-387. [11] Kanchibotla S S, Valery W, Morrell S. Modelling fines in blast fragmentation and its impact on crushing and grinding[C]∥Proceedings of Explo’99-A Conference on Rock Breaking. Kalgoorlie, Australia, 1999:137-181. [12] Esen S, Onederra I, Bilgin H A. Modelling the size of the crushed zone around a blast hole[J]. International Journal of Rock Mechanics and Mining Sciences, 2003,40(4):485-495. [13] 戴俊.岩石动力学特性与爆破理论[M].北京:冶金工业出版社,2002. [14] Hagan T N, Gibson I M. Lower blasthole pressures: A means of reducing costs when blasting rocks of low to moderate strength[J]. International Journal of Mining and Geological Engineering, 1988,6(1):1-13. [15] Ghosh A. Fractal and numerical models of explosive rock fragmentation[D]. Tucson: The University of Arizona, 1990. [16] Rakishev B, Rakisheva Z B. Basic characteristics of the stages of rock massif destruction by explosive crushing[C]∥Asia-Pacific Symposium on Blasting Techniques. Kunming, China, 2011:65-69. [17] 亨利奇.爆炸动力学及其应用[M].熊建国,等,译.北京:科学出版社,1987. [18] 杨善元.岩石爆破动力学基础[M].北京:煤炭工业出版社,1991. [19] Olsson M, Bergqvist I. Crack lengths from explosives in multiple hole blasting[C]∥The Fifth International Symposium on Rock Fragmentation by Blasting. Montreal, Quebec, Canada, 1996:187-191. [20] Slaughter S. Investigation of coal fines[R]. Internal Report, Julius Kruttschnitt Mineral Research Centre (JKMRC), Australia, 1991. (责任编辑 曾月蓉) Improved calculation model for the size of crushed zone around blasthole Leng Zhen-dong1,2, Lu Wen-bo1,2, Chen Ming1,2, Yan Peng1,2, Hu Ying-guo1,2 (1.StateKeyLaboratoryofWaterResourcesandHydropowerEngineeringScience,WuhanUniversity,Wuhan430072,Hubei,China; 2.KeyLaboratoryofRockMechanicsinHydraulicStructuralEngineeringMinistryofEducation,WuhanUniversity,Wuhan430072,Hubei,China) To explore the breakage mechanism of rocks around the blasthole and to accurately predict the size of the crushed zone in drilling and blasting, an improved calculation model for calculation the size of the crushed zone was presented. The four-region model was established with hoop compressive stress in the inner part of fractured zone and cavity expansion effect taken into account. The material in the crushed zone is assumed to be granular medium without cohesion but with internal friction. On this basis, the formula for the crushed zone radius in drilling blasting is derived by elastic-plastic mechanics theory. The analysis shows that the size of the crushed zone ranges from 1.2 to 5.0 times of the blasthole radius, and there are notable discrepancies among rock types. Compared with other models, the improved model is in better agreement with the experiment data. mechanics of explosion; calculation model; hoop stress; crushed zone; improvement; cavity expansion 10.11883/1001-1455(2015)01-0101-07 2013-05-03; 2013-07-25 国家自然科学基金项目(51125037,51279135); 国家重点基础研究发展计划(973计划)项目(2011CB013501); 高等学校博士学科点专项科研基金项目(20110141110026) 冷振东(1989— ),男,博士研究生;通讯作者: 卢文波,wblu@whu.edu.cn。 O383.1;TV554 国标学科代码: 13035 A2 公式推导
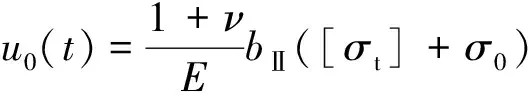
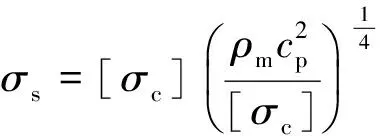
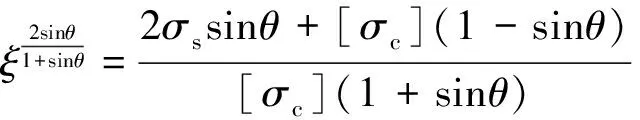
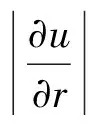
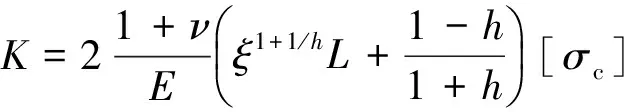
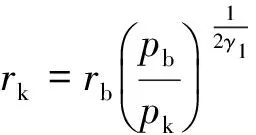
3 不同计算模型对比
4 与实验结果的对比
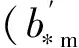
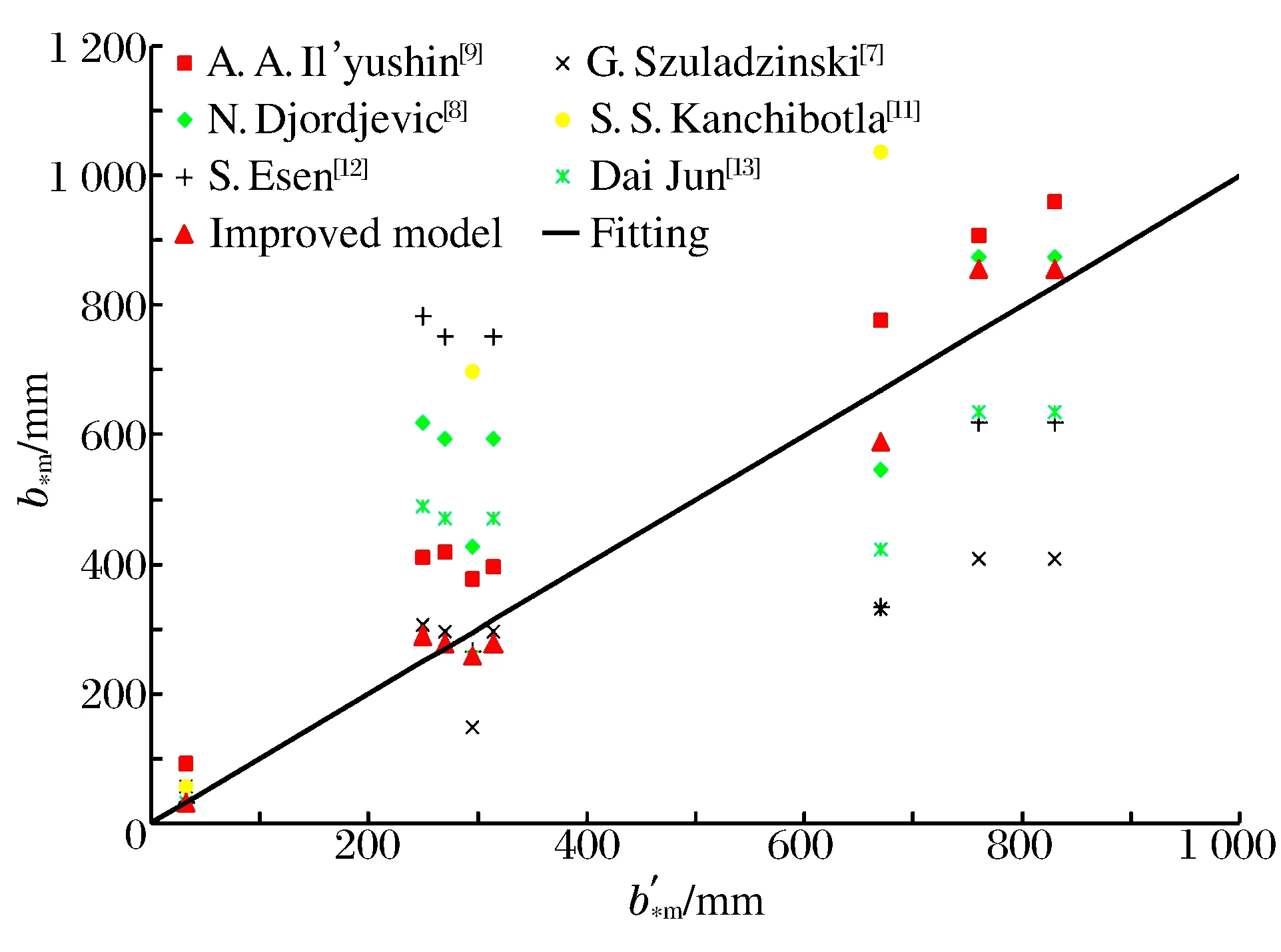
5 结论与讨论

