基于CPS的建筑环境数据级检测融合方法

陈浩男　马斌　王长涛　刘钊　溥博文

摘 要： 针对建筑环境CPS数据级融合可靠性的问题，采用线性最小方差估计的方法对传统自适应加权融合算法进行改进，不仅减小了均方误差，而且使得融合结果可靠性更高。在数据融合前进行限幅处理，判断数据是否异常，对异常数据的加权因子进行配置处理，既提高了数据的筛选性，又保证了系统数据融合结果的可靠性。仿真实验表明了该方法的有效性。

关键词： 建筑环境； 信息物理融合系统； 数据级融合； 自适应加权融合算法； 线性最小方差； 限幅滤波

中图分类号： TN911.23?34； TP274+.2 文献标识码： A 文章编号： 1004?373X（2015）01?0096?04

Abstract： For problem of CPS data level fusion reliability in built environment， the way of linear minimum variance estimation is used to improve the tradition adaptive weighted fusion algorithm， which not only reduces the mean square error， but also makes the fusion result more reliable. The amplitude limiting process should be carried out before data fusion， so as to determine whether data is abnormal and allocate weighting factor of the abnormal data， which can improve the filtration ability of the data and ensure the reliability of the data fusion result. The simulation experiment indicated the effectiveness of the way.

Keywords： built environment； cyber?physical systems； data level fusion； adaptive weighted fusion algorithm； linear minimum variance； amplitude limiting filtering

0 引 言

建筑环境CPS数据级融合的可靠性是对建筑环境能否做出正确评价以及决策的一个重要保证，很多时候衡量这一标准的重要指标是均方误差，均方误差越小，说明融合估计结果越好。传统建筑环境数据级融合采用了一些估计方法来减少均方误差，只注重对已经接收到的数据进行处理来提高融合的可靠程度，却往往忽略接收到的数据是否有处理的价值。信息物理融合系统（Cyber?Physical Systems）[1?3]是在环境感知的基础上，将通信、计算和控制进行深度融合的可控可信可扩展的网络化系统，检测数据的可靠性将直接影响CPS的运行效果。如何判断传感器是否异常，进一步减小均方误差，以及解决传感器工作异常的问题，对于提高建筑环境CPS数据级融合的可靠性是十分必要的。

目前国内外的学者研究建筑环境系统数据级融合的算法主要有加权融合算法、加权平均法[4]、自适应加权融合算法[5]、贝叶斯推理算法[6]等。其中加权融合算法实现容易，但加权因子不好确定，一般都根据经验来赋值[7]。加权平均法操作同样简单，但误差较大不适合高精度的数据融合[8]。自适应加权融合算法可以不需要任何先验知识的前提下进行融合，该输出值均方误差较小[9]，在一定的程度上，提高了数据级融合的可靠性，但对融合数据的筛选性较差。贝叶斯推理算法适用于在具有可加高斯噪声等不确定性信息时的处理，但是该算法定义先验似然函数比较困难、缺乏不确定性能力[10]。

以上算法均不能满足建筑环境CPS数据级要求，针对这种情况，本文利用线性最小方差估计的方法，结合自适应加权融合算法的特点，将二者进行融合。融合后的算法相对于原自适应加权融合算法均方误差减小，融合精度更高。并将改进后的融合算法与限幅处理思想相结合，来判断传感器检测到的数据是否异常，据此改变融合算法中相对应的加权因子。这样，在一定程度上保证了建筑环境CPS数据级融合输出的可靠性。

1 传统自适应加权融合算法简介

自适应加权融合算法的优点是对即时采集的数据进行处理，在无偏估计准则下，该算法可以在不知道传感器测量数据的任何先验知识的条件下，单靠传感器提供的即时数据，就能使融合出的数据融合值均方误差较小[11]。

3 限幅处理法

限幅滤波法是判断被测信号的变化，据此消除缓变信号中的尖脉冲干扰。其基本思想为，根据已有的时域采样结果，将本次采样值与上次采样值进行比较，差值超出允许范围的，就认定该值异常[12]。

本文利用这一思想对采集数据进行处理。在假设传感器失灵的总数不会超过整个传感器数目的一半的基础上，将不同传感器测量的即时数据进行相互比较，如果它们的差值小于规定的允许范围，则认为各传感器均正常工作，可以将它们采集到的数据进行正常的处理；一旦发现有差值大于规定的允许范围的情况，则表示有传感器出现异常情况。

4 限幅处理与改进后的自适应加权算法的

融合算法

数据融合过程中很多时候会发生传感器异常导致采集数据偏差很大，针对这一问题，本文采用了限幅处理法补充改进后的自适应加权融合算法，使其可以在融合前发现异常数据，并且改变对应的加权因子，从而保证了数据级融合数据的可靠性。

4.1 结构与流程

限幅处理与改进后的自适应加权算法融合后形成了新的算法，新算法可以解决如何提前发现并且处理因传感器异常导致的采集的数据偏差较大的问题。算法的整体结构如图3所示。

由图3可以看出，在改进自适应加权融合算法的前面添加了限幅处理模块，该模块对传感器检测的数据进行比较检测后，在一定的条件下可以通过各个检测数据来判断相对应的传感器是否发生失灵异常。异常则修改相应的加权因子来保证融合输出更加可靠的数据[Z（k）。]算法步骤如下：

（1） 用限幅处理法来检测是否有传感器失灵异常。有则找出相对应的传感器，并在公式（4）中将对应的加权因子直接设定为零。

（2） 由公式（7）求出各个传感器的均方方差[σ2i（k）。]

（3） 由公式（4）求出各个传感器的最优加权因子[Wi，i=1，2，…，n。]

（4） 由公式（1）求出最终多传感器的融合结果[Z（k）]。

算法的流程图如图4所示。

4.2 仿真实验

本文的限幅处理模块算法满足仿真2.2实验环境条件，通过观察加权因子和融合输出值的输出来验证本文算法是否合理。

本文仍然选用3组数据来模拟湿度触感器测量数据，并假设用来模拟湿度的估计真值为31，正常的误差范围[α≤2。]正常传感器的误差分别为0.6，0.36，失灵异常为3，选200个时刻作为采样时刻。图5，图6分别为传统无限幅处理自适应加权融合算法的加权因子和有限幅处理的自适应加权融合因子。

通过图5，图6比较可以看出，有限幅处理的自适应加权融合算法的传感器3加权因子为零，这是因为通过限幅处理模块的检测，判断出传感器3工作异常，检测的数据不可靠，系统自动将其加权因子设为零，阻止其继续参与数据融合工作。无限幅处理的自适应加权融合算法不具备该功能，误差数据仍参与输出。

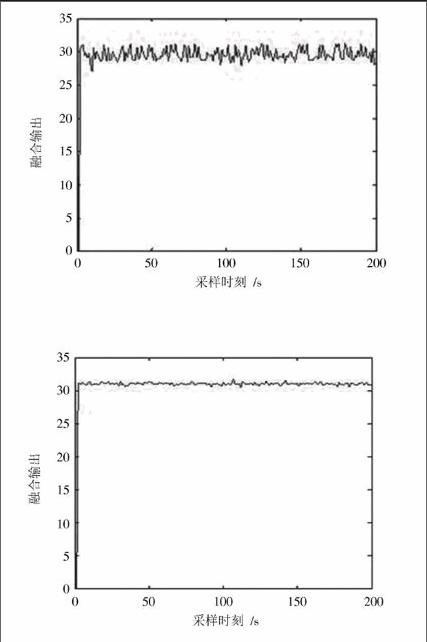
图7～图9分别为有异常的传统自适应加权融合算法、有异常时无限幅处理模块改进自适应加权融合算法和有异常时有限幅处理模块的改进自适应加权融合算法的融合输出图。

通过图7～图9可以看出当传感器异常时，原自适应加权融合算法输出偏离估计真值较远，是因为算法没对异常数据处理，异常数据的加入使得均方误差偏大，导致输出可靠性不高。改进后的自适应加权融合算法相对于原自适应加权融合算法的输出接近估计真值，可靠性有所提高，均方误差也减小，因为异常数据的参与，仍然偏离估计真值，可靠性不最高。加入限幅处理模块后的改进自适应加权融合算法即减小了均方误差，且利用限幅处理模块去掉了异常数据，提高了可靠性，使输出更加贴近估计真值，可以应用在建筑环境中。

5 结 语

本文利用了线性最小方差估计方法的特点，并与自适应加权融合算法相结合，改变了原均方误差的计算方法，使得改进后的均方误差小于改进前，提高了融合精度、输出稳定性。并在此基础上，添加了限幅处理模块，可以对传感器采集的数据做出处理，消除了误差较大数据的影响，进一步提高了输出数据的可信度，从而保证了在建筑环境下CPS数据级处理检测数据的可靠性。

参考文献

[1] 温景容，武穆清，宿景芳.信息物理融合系统[J].自动化学报，2012，38（4）：507?517.

[2] 马斌，李楠楠.基于人工神经元方式构建的信息物理融合系统[J].沈阳建筑大学学报：自然科学版，2012（3）：375?379.

[3] LEE E A. Cyber physical systems： design challenges [C]// 2008 11th IEEE International Symposium on Object Oriented Real?time Distributed Computing （ISORC）. Orlando， Fl： IEEE， 2008： 363?369.

[4] 刘海斌，宫峰勋.一种改进的多传感器加权融合算法[J].电子产品世界，2009（12）：19?21.

[5] 崔翌立，戴逸松.多传感器数据自适应加权融合估计算法的研究[J].计量学报，1998（1）：70?74.

[6] DURANT?WHYTE H F. Consistent integration and propagation of disparate sensor observations [J]. International Journal of Robotics Res，1987， 6（3）： 2?24.

[7] 邓蕴昊，张纳温.一种改进的加权融合算法[J].弹箭与制导学报，2008（12）：311?313.

[8] 张雨，温熙森.设备故障信息融合问题的思考[J].长沙交通学院学报，1999（4）：22?29.

[9] 金建华，阙沛文.多传感器测量数据的切尾加权融合算法[J].仪器仪表学报，2002（6）：301?304.

[10] 张廷龙，王俊勇.多传感器数据融合技术概述[J].舰船电子工程，2013（2）：41?44.

[11] 张晓亮，罗文广.多传感器数据融合技术在室内环境品质监控系统中的应用[J].仪表技术与传感器，2012（2）：103?105.

[12] 郭铁梁，赵旦峰，钱晋希.OFDM水声通信降低限幅噪声的改进算法[J].计算机工程与应用，2013，49（14）：15?18.