数字化振动台激振系统建模与仿真研究

李 睿 孙劲涛

（西安建筑科技大学土木工程学院，陕西 西安710055）

0 引言

地震模拟振动台是一种能够较为真实地再现和模拟地震对试件作用的实验仪器，也是在结构抗震实验方法中应用最广泛的实验仪器之一［1］。激振系统是振动台的出力装置，随着机械研究的发展，振动台的复杂程度和要求的精度越来越高，这就促使对激振系统的研究成为一个重要课题。在激振大型结构时，为得到较大的响应，需要很大的激振力，也往往采用电液式激振器［2－5］。

目前，三轴六自由度地震模拟振动台多为8套激振器（X、Y 向各2套，Z 向4套）。西安建筑科技大学的刘璇［6］通过研究振动台液压系统的工作原理，建立了地震模拟振动台液压系统的仿真模型。哈尔滨工业大学的关广丰［7］从运动学的角度出发，对振动台的实验系统进行了深入的研究。

本文对激振系统进行数学建模，并根据实验数据拟合作动器中的未知参数。最后利用已经建好的Simulink模型和作动器动力学模型进行仿真，将输出结果与实验室结果进行对比，判断仿真模型的正确性。

1 激振系统数学模型的建立

1.1 液压缸数学模型

当液压缸中油液体积发生变化而产生推动力时，会推动活塞杆做活塞运动，使振动台产生相应的位移，下面研究液压缸内部力的传递，寻找体积改变与输入位移的数学关系，建立模型。

液压作动器的基本构造是一个双驱动作动器，它主体为等体积圆柱油缸，在油缸上安装有控制流量的阀门。根据液压缸的物理模型，流量的变换引起了体积变化，体积变化推动了活塞产生位移，得伺服阀缸内油压、流量与位移的方程为：

式中，p1为供油压力；p2为进油腔压力；A 为活塞杆的截面面积；B 为液体体积弹性模量；Cl为活塞泄漏系数；Cb为活塞渗流系数；

作动器液压缸中体积改变v1、v2公式为：

式中，V 为缓冲柱塞与缓冲孔间隙中油的体积；yc为活塞的位移量，其初始值为零位置。

由液压缸体积变化引起的输出力被定义为：

1.2 作动器数学模型

由于作动器的行程较短，其整体几何非线性较小，故作动器的机械模型采用近似线性模型［8］，如图1所示。

图1 作动器结构和符号示意图

为了方便表示，将作动器驱动位移记为Yt，而拉杆的变形长度记为Yp，液压缸的变形长度记为Ym，液压作动器实际伸长的长度记为Yc。另外Ya、Yc、Ym、Yp为作动器平衡状态时的各部分位移（即作动器无任何力输出且输出位移为0时的状态），各自的改变量表示为yt、ya、yc、ym、yp。

根据最终位移的各组成部分，分别对液压缸和拉杆建立方程。对于液压缸根据力平衡得：

对于给台体施加力的活塞杆的位移：

由于相对于整个振动台的台体来说活塞杆的质量较小，可以忽略不计，因此计算时忽略活塞杆自身的惯性响应。

假设ft为作动器施加在台体上的外力：

将式（7）代入式（6）得：

整理式（9）得：

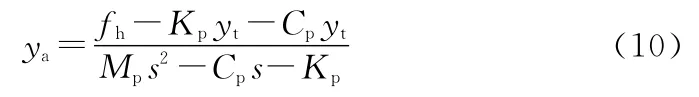
由式（10）和式（6）可得作动器最后的实际输出值yc的最终表达式为：

其物理含义为作动器驱动臂克服本身动力特性后的实际输出值。

2 内部参数估计

在对作动器建立模型时，将液体油视为理想液体，即没有黏性、没有压缩性。为了简化研究、便于分析，文中对液体及其流动做了一些假设。但是这样做的结果必然与实际有较大误差，为尽量减小误差，将根据实际情况对油层流动的结果加以适当修正，使其与实际情况接近。下面将对作动器油缸中油量的不可压缩性和无泄漏等问题进行研究，并对其做出估计。

忽略阀内损失和气门重叠，简化阀门流量q的方程式为：

式中，x＝V（s）u。

由图1所示可知，把yc分解成两部分后可以把公式写成：

由于引入了对模拟结果影响较大的参数，作动器的线性模型中引入了可压缩油缸刚度Kh和油液在作动器中泄漏和层流变化系数Ch，各参数具体含义如图1所示。

因此，把式（10）代入式（13）可得：

式中，f＝F（s）yc。

整理后可得：

通过对g、d、e 3个参数的估计可以得出未知的可压缩油缸刚度Kh和油在作动器中泄漏和层流变化系数Ch。采用最小二乘法进行参数的拟合，最后得出各参数取值如下：Kv＝1.75×Ch＝8 410kNs/m，Kh＝715kN/mm。

3 数字化振动台激振系统整体仿真模型构建及仿真分析

前面对激振系统建立了数学模型，下面利用MATLAB/Simulink建立数字化振动台激振系统整体仿真模型。仿真模型中包括平台轨迹位置算法模块、控制系统模块、激振器仿真模块、输入输出模块［9］。

本文重点对单个激振器进行机械动力学建模，SimMechanics模型如图2所示，在仿真模型中对相应参数进行设置［10－12］，各参数取值如表1所示。

表1 伺服液压系统数学模型参数值

这里主要是对现有的模型与实验室采集到的数据进行比较和对比。向模型中输入X 方向自由度的波形为X ＝2×sin（5×t）mm，得到波形如图3所示。

图2 作动器仿真模型

图3 X 方向仿真曲线

Y 方向与X 方向类似（图4），不作过多分析。

图4 Y 方向仿真曲线

向模型中输入Z 方向自由度的波形为Z ＝2×sin（5×t）mm，Z 方向的输出曲线如图5所示，Z1～Z4作动器位移一致，X、Y 方向作动器有较小的位移输出。Z 方向平动自由度合成比较稳定，但Z 方向的转动自由度有较小位移输出。

图5 Z方向仿真曲线

通过上面对各作动器的位移分析可以看出，数学模型和作动器采集的数据整体趋势基本相同，但实际采集数据的过程中可能会有不确定因素的消耗，所以实测数据相对于模型来说峰值较小，同时在作动器实体模型中，由于各子系统响应时间存在差异，会产生相对的时间差值，在数学模型中应加入一定的延迟，但时间相对不确定，两图相比在周期不变的情况下实体模型有一定滞后的时间。

4 结语

本文首先根据信号传递的过程把数字化振动台的激振系统分为液压缸、作动器两部件。随后根据各部件的物理、力学及工作特性，分别建立了各自的数学模型。在各自数学模型的基础上，推导出位移输入和作动器输出的数学关系。然后，对各个部件建立数学模型，其中考虑了液体油的压缩和流层的泄漏等重要因素的影响。根据所采集的振动台空负荷下的实验数据所做的频响反应，估计出相应的已知或未知的参数值或相应的取值范围，从而为数字化振动台设计过程提供所需参数。最后利用MATLAB/Simulink对激振系统模型进行仿真分析。通过空台上采集的实验数据与模拟数据的对比，验证了模拟的正确性。

［1］王向英.结构地震模拟振动台混合实验方法研究［D］.哈尔滨：哈尔滨工业大学，2010.

［2］黄长艺，严普强.机械工程测试技术基础［M］.北京：机械工业出版社，1985.

［3］SHIMIZU N，SHINOHARA Y，YABUKI H，et al.Control Simulation of Shaking Table with Non－linear Structure［C］//Proceedings of ACMD，2004.

［4］CONTEL J P，TROMBET T L.Linear Dynamic Modeling of a Uniaxial Servo－hydraulic Shaking Table System［J］.Journal of Earthquake Engineering and Structural Dynamics，2000，29：1375－1404.

［5］THOEN Bradford K，LAPLACE Patrick N.Offline Tuning of Shaking Tables［C］//13th World Conference on Earthquake Engineering，2004.

［6］刘璇.基于Simulink的数字化地震模拟振动台仿真方法研究［D］.西安：西安建筑科技大学，2013.

［7］关广丰.液压驱动六自由度振动试验系统控制策略研究［D］.哈尔滨：哈尔滨工业大学，2007.

［8］Plummer A R.A Detailed Dynamic Model of a Six－Axis Shaking Table［J］.Journal of Earthquake Engineering，2008，12（4）：631－662.

［9］陈云.基于SimMechanics和VRML 的6－dof并联振动平台的运动仿真［D］.长春：吉林大学，2012.

［10］张镭，丛大成，姜洪洲，等.一种基于SimMechanics CAD 转换器生成虚拟样机的方法［J］.系统仿真学报，2007，19（20）：4699－4703.

［11］姚太克.一类三自由度并联机构的特性研究与优化设计［D］.合肥：中国科学技术大学，2013.

［12］黄晓敏.基于Matlab的六自由度平台研究［D］.广州：华南理工大学，2013.