整函数及其微分多项式权分担1 值的唯一性①

甘 媛

(福建船政交通职业学院公共教学部，福建福州350007)

1 引言及主要结果

定理［1］: 若f，g 为两个非常数整函数，正整数n，k 满足n ＞2k+4.如果(fn)(k)与(gn)(k)以1为CM 公共值，则f=c1ecz，g=c2e－cz或f=tg;其中c，c1，c2，t 为满足(－1)k(c1c2)n(nc)2k=1 及tn=1的常数.

将上述定理中的CM 分担值用权分担的思想，讨论了(fn)(k)与(gn)(k)权分担1 值问题，得到以下结果:

定理1.1: 若f，g 为两个非常数整函数，正整数n，k 满足如果(fn)(k)与(gn)(k)分担(1，1)，则f=c1ecz，g=c2e－cz或者f=tg;其中c，c1，c2，t 为满足(－1)k(c1c2)n(nc)2k=1 及tn=1 的常数.

定理1.2: 若f，g 为两个非常数整函数，正整数n，k 满足n ＞3k+4.如果(fn)(k)与(gn)(k)分担(1，2)，那么定理1.1 的结论成立.

2 主要引理及其证明

引理2.1: 若两个整函数F，G 分担(1，1)，那么

证明:

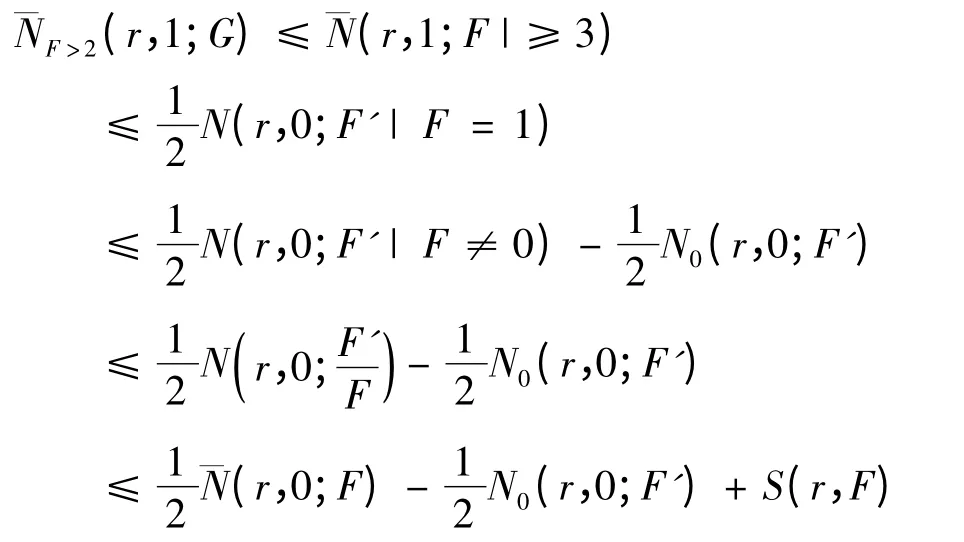
同理可证后一个式子.

引理2.2: 若两个非常数整函数F，G 分担(1，2)，那么

证明: 由N0(r，0;G′)的定义及F，G 分担(1，2)，有

于是得到:

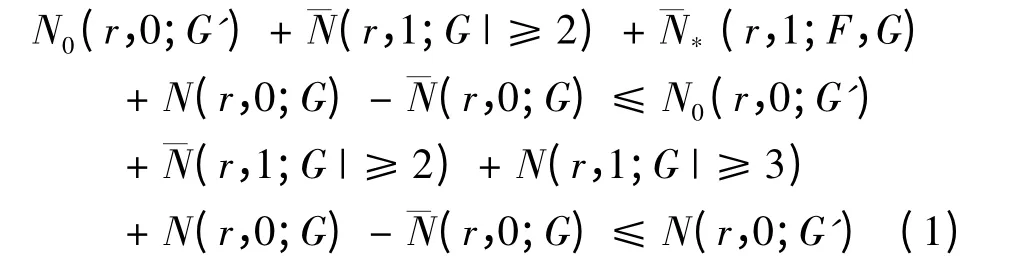
由Nevanlinna 关于亚纯函数的第一基本定理及Milloux 定理［2］有

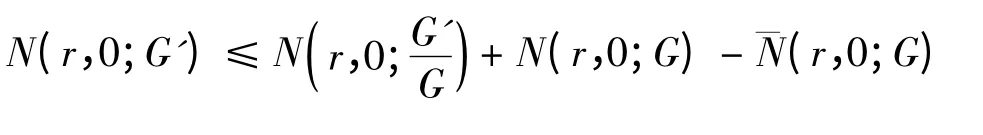
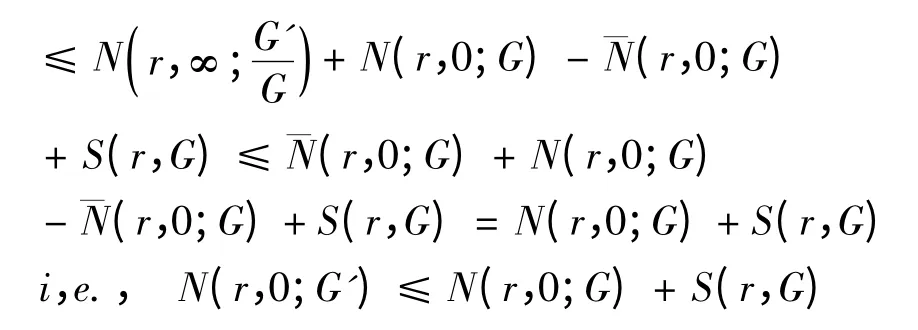
根据上式及(1)，我们可以证明引理2.2.

引理2.3: 若f，g 为两个非常数整函数，k 为正整数，如果f(k)与g(k)分担(1，l)，(i)若l=1，

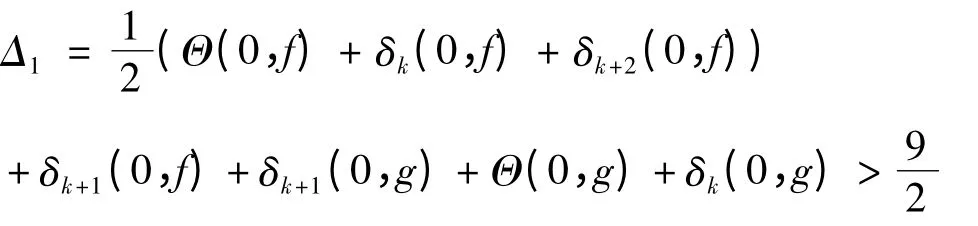
(ii)若l=2，

Δ2=Θ(0，f)+δk(0，f)+δk+1(0，f)+δk+2(0，g)＞3;

那么f(k)g(k)≡1 或者f ≡g.

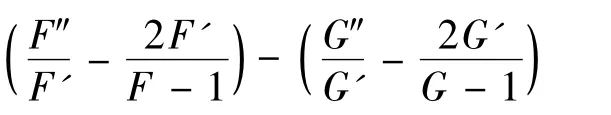
情形1:l=1.因此F，G 分担(1，1).

由引理2.1，

由文献［3］，(2)变为

那么

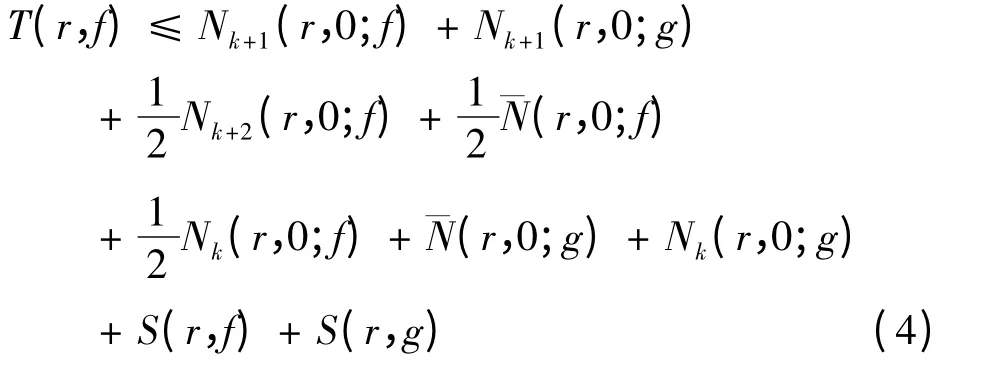
不妨设，存在一具有无限测试的集合I 使得T(r，g)≤T(r，f)，当r ∈I.因此:

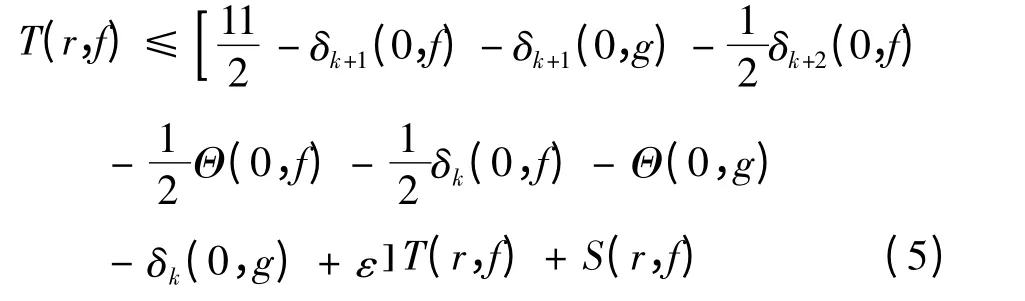
因此得到H ≡0.

情形2:l=2.那么F，G 分担(1，2)，于是¯N(r，1;F|≥2)=¯N(r，1;G|≥2).

根据参考文献［4］和［5］与引理2.2，得到

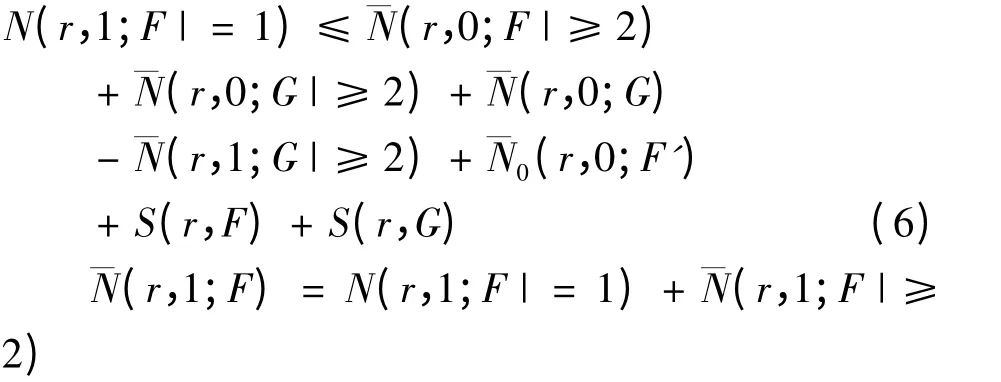
根据参考文献［2］和［3］以及F=f(k)与G=，有

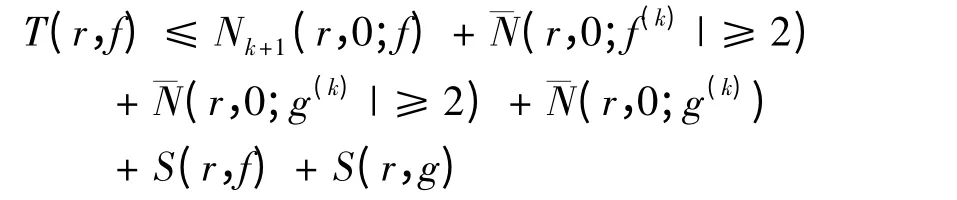
于是

不妨设，存在一具有无限测试的集合I 使得T(r，g)≤T(r，f)，当r ∈I.因此

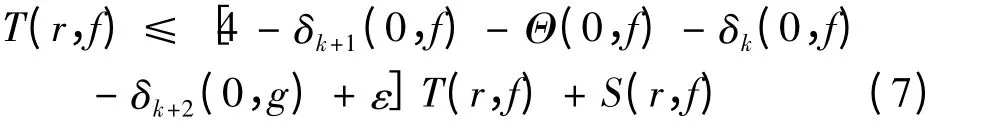
当r ∈I 及0 ＜ε ＜Δ2－3.这样由(7)有{Δ2－3－ε}T(r，f)≤S(r，f)i，e.Δ2≤3，由Δ2＞3 得到矛盾.

因此得到H ≡0.

3 定理的证明

令F=fn，G=gn.

因为

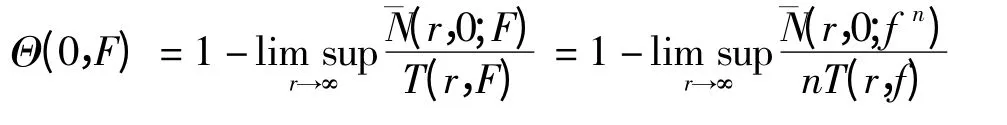
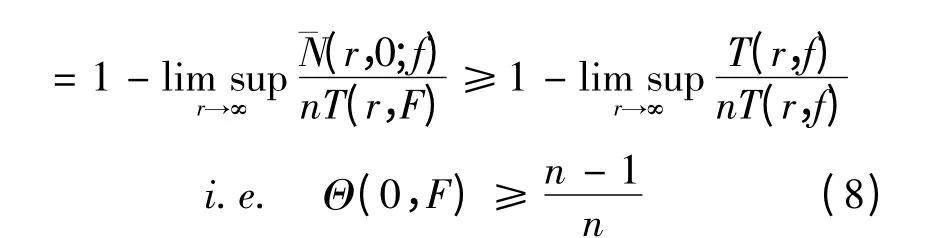
类似地有:

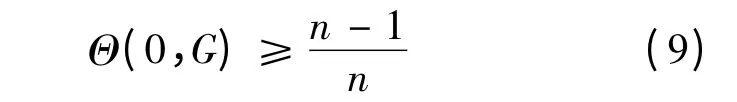
由Nk(r，a;f)的定义知

因此，

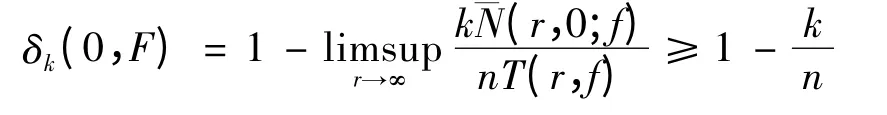
类似地有:

以及

由(8)～(13)得到

由于F(k)=(fn)(k)及G(k)=(gn)(k)，根据定理1.1 的条件知，F(k)，G(k)分担(1，1)且F，G 满足引理2.3 的条件，这样可以得到F(k)G(k)≡1 或者F≡G.

由(8)～(13)，有

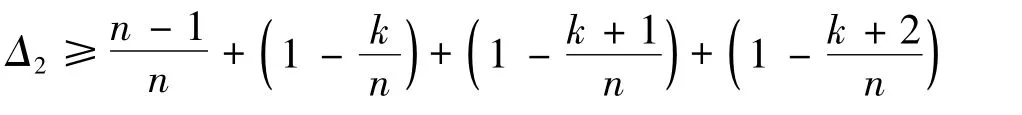
由n ＞3k+4 得Δ2＞3

由于F(k)=(fn)(k)及G(k)=(gn)(k)，根据定理1.2 的条件知，F(k)，G(k)分担(1，2)且F，G 满足引理2.3 的条件，这样可以得到F(k)G(k)≡1 或者F≡G.

［1］ M.L.Fang.Uniqueness and Value－Sharing of Entire Functions［J］.Comput.Math.Appl，2002，44:823－831.

［2］ W.K.Hayman，Meromorphic Functions［M］.Oxford:The Clarendon Press，1964.

［3］ H.X.Yi.C.C.Yang，Uniqueness Theory of Meromorphic Functions［M］.Beijing:Science Press，1995.

［4］ I.Lahiri.Weighted Value Sharing and Uniqueness of Meromorphic Functions［J］.Complex Variables Theory Appl，2001，46:241－253.

［5］ A.Banerjee.Meromorphic Functions Sharing One Value，Int.J.Math.Sci.2005:22(2005):3587－3598.(i)l=1 andl=2 and n ＞3k+4;satisfied，then either f=c1ecz，g=c2e－czwhere c，c1，and c2are three constants satisfying(－1)k(c1c2)n(nc)2k=1 or f(z)=tg(z)for a constant t such that tn=1.