框架承担的倾覆力矩比例对框架—剪力墙结构抗震性能的影响①

刘志远，巢 斯

(1.同济大学土木工程学院建筑工程系 上海200092;2.同济大学建筑设计研究院(集团)有限公司 上海200092)

1 模型的建立

1.1 计算模型

结构模型为抗震设防烈度为7 度(0.1g)地区，各层层高均为3.0m 的12 层的框架－剪力墙房屋，总高度为36.0m.该模型平面形状呈矩形.结构立面布置和结构平面布置如图1 和图2.

1.2 结构设计

本文各计算模型均按照中国有关规范进行设计，使结构满足规范中的各项指标.在此基础上，通过改变梁高、柱和剪力墙截面的大小来改变框架部分所承担的倾覆力矩的比例.本文一共建立了5 个相似的模型，采用了不同的主梁截面、柱截面以及剪力墙截面，结构布置大体相同.各模型主梁、柱和剪力墙截面参数如表1 所示.

表1 模型截面参数

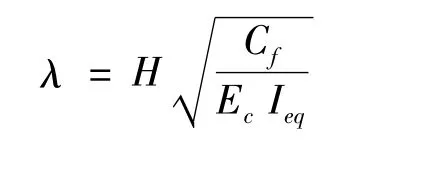
式中:H 为结构的总高度;Cf为总框架的剪切刚度;EcIeq为剪力墙的等效刚度［1］.

1.3 材料的本构关系

1.3.1 混凝土

在本文中，混凝土的本构关系采用《混凝土结构设计规范》(GB50010－2010)附录C 的受压曲线［2］.取FU 值为混凝土单轴抗压强度平均值，FY值为FU 的30%，R 点的强度取值为FU 值的20%.对应Y，U，L，R，X 位置的混凝土耗能退化系数分别取1.0，0.9，0.7，0.4，0.3，不考虑混凝土受拉.

1.3.2 钢筋和钢材

如图3 所示，钢筋和钢材本构模型采用三折线模型，强化段的弹性模量取0.01Es，Es 为钢筋的初始弹性模量，不考虑过极限点的应力衰减.

图1 结构总体模型

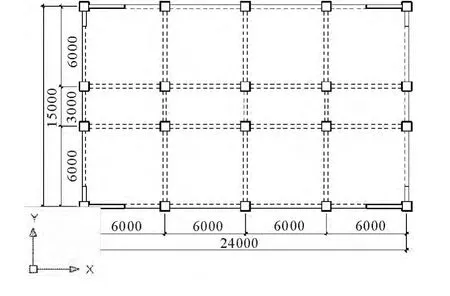
图2 结构平面布置图

1.4 结构构件模拟

在本文的5 个算例中，对框架梁单元采用塑性铰模型，对于剪力墙和框架柱单元，则采用纤维模型模拟.

2 结构整体性能指标及评价

2.1 弹性分析结果

在进行弹塑性分析之前，对各模型进行了弹性分析，比较了各模型的周期、层间位移、基底剪力等.(结果见表2、图4 和图5)

图3 钢筋和钢材本构关系模型

表2 各模型弹性分析结果

图4 结构层间位移角曲线

由以上结果可以看出，各个模型的最大层间位移角和周期相差不多，说明各模型的侧向刚度相差不大，在这样的前提下后续的分析结果才具有比较性.当框架的倾覆力矩百分比较小时(例如模型1和模型2)，结构性能接近于剪力墙结构，变形也接近于弯曲形，因而结构下部层间位移角较小而结构上部层间位移角较大.随着框架倾覆力矩百分比的提高，结构变形性质逐渐向框架结构靠拢，结构上部层间位移角随着框架倾覆力矩百分比的增大，结构上部层间位移角越来越小.

2.2 弹塑性时程分析结果

为充分考虑不同地震波输入对计算结果的影响，本文选取了三条《上海抗震规程》附录中的地震波(两条天然波和一条人工波)分别对这5 个模型进行弹塑性时程分析.各模型在7 度大震下弹塑性时程分析的最大层间位移角如下表所示:

表3 各模型弹塑性时程分析最大层间位移角

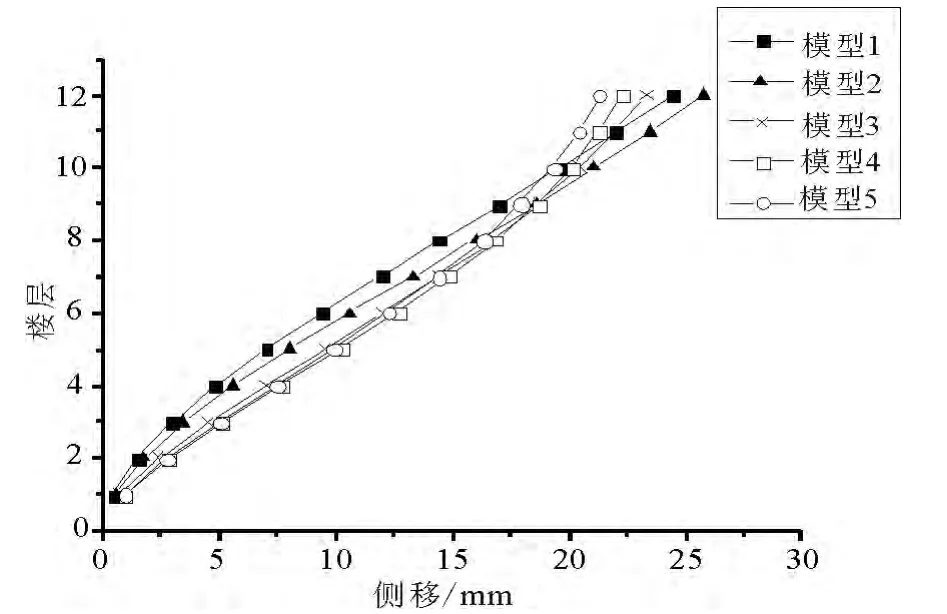
图5 结构侧移曲线

由以上时程分析结果可以看出:各个模型在7度罕遇地震水准下的层间位移角均能满足规范的相关规定;随着结构的框架倾覆弯矩比例的增加，结构的最大层间位移角呈变大的趋势.

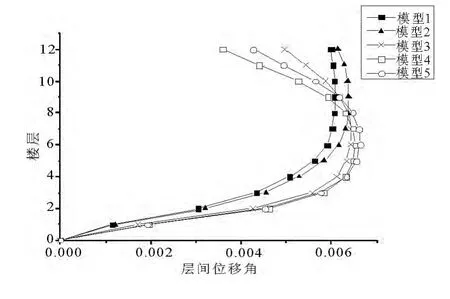
图6 弹塑性时程分析层间位移角曲线

2.3 损伤性能指标

Ghobarah 提出了一种评价结构刚度变化的计算方法，并把这种量化值作为评价结构损伤程度的指标，从而反应出结构的抗震性能(如图7 所示)［3］.在管民生，韩大建，杜宏彪《钢筋混凝土框架结构的抗震性能指标》以及黄维，钱江，庄彬彬《基于两次推服分析考虑损伤效应的结构抗震评估报告》等文中对上述指标评价方法进行了更深入的阐述及应用［4～5］.该方法需要对结构进行两次静力弹塑性分析，第一次是结构遭受地震作用前，第二次是在结构遭受地震作用后.再分别绘出两次静力弹塑性分析的(基底剪力/结构总重量)—(顶点位移/结构总高度)曲线，由式(1)可计算出该性能指标.

图7 静力弹塑性分析损伤性能指标计算简图

结构的整体性能指标(DI)k由式(1)计算得:

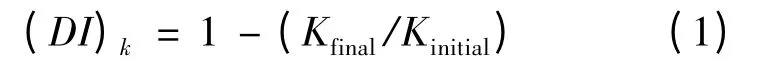
式中:Kinitial为地震前结构Pushover 曲线的初始斜率，Kfinal为地震后结构的Pushover 曲线的初始斜率［5～6］.

结构性能指标(DI)k按照结构损伤大小从0 至1 变化，0 表示结构无损伤，1 表示结构倒塌，损伤最大，不可修复.具体指标关系见表4 所示.

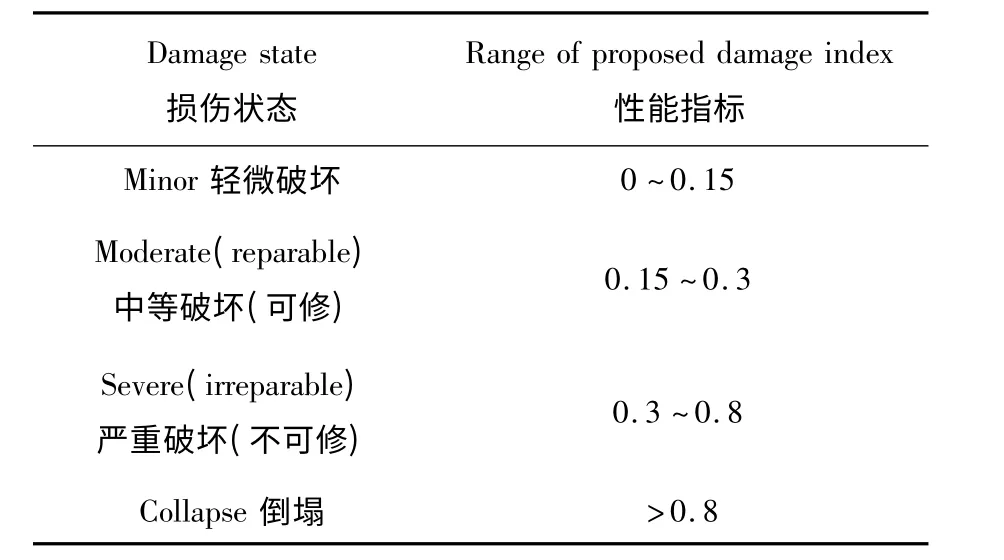
表4 结构性能水准与性能指标［3］

结构在遭受等同于7 度罕遇地震水准的地震荷载后，结构加载时的初始刚度明显小于无损伤加载的初始刚度.反映出结构在罕遇地震作用下经历了较大的非弹性变形，产生的损伤较大.现将这5个模型的Ghobarah 指标汇总见表5.

表5 模型损伤性能指标汇总

从以上计算结果可以看出，模型1 损伤性能指标最小，为0.072.模型5 损伤性能指标最大，为0.222.模型5 的损伤性能指标略大于模型4，这与模型5 的框架倾覆力矩百分比略大于模型4 的客观条件相呼应，从这个方面反映出软件分析和模型的正确性.随着结构的框架倾覆弯矩比例的增加，结构的损伤性能指标也增大.

3 结 论

本文建立了5 个框架—剪力墙模型，在保证各个模型的侧向刚度基本相同的前提下，通过调整各个模型的剪力墙墙肢的截面大小，框架柱和框架梁截面大小，改变框架所承担的倾覆力矩百分比.用PERFORM－3D 有限元程序对模型进行两次Pushover 分析，即地震前分析和罕遇地震作用后分析，再利用Ghobarah 指标评价各个模型的损伤程度，以此来判断框架倾覆力矩百分比对结构抗震性能的影响.

(1)由表5 的计算结果可知，随着结构的框架

倾覆弯矩比例的增加，结构的损伤性能指标越大.说明对于框架—剪力墙结构，框架的倾覆弯矩百分比越高，对整个结构的抗震性能越不利.

(2)在设计框架—剪力墙结构时，要尽量控制框架的倾覆力矩百分比，使剪力墙承担大部分倾覆力矩，这样结构设计会比较安全.

(3)在保持框架—剪力墙结构总体抗侧刚度基本不变的前提下，增加剪力墙的数量，减少框架倾覆力矩的比例，对提高结构抗震性能起到有利的作用.

［1］ 史庆轩，梁兴文.高层建筑结构设计［M］.北京:科学出版社，2006.

［2］ GB50010—2010 混凝土结构设计规范［S］.北京:中国建筑工业出版社，2011.

［3］ Ghobarah A.，Abou－Elfath H.，Biddah A.Response－based Damage Assessment ofStructures［J］.Earthquake Engineering and Structural Dynamics，1999，28(1):79－104.

［4］ 管民生，韩大建，杜宏彪.钢筋混凝土框架结构的抗震性能指标研究［J］.深圳大学学报理工版，2011，28(3):200－206.

［5］ 黄维，钱江，庄彬彬.基于两次推覆分析考虑损伤效应的结构抗震性能评估［J］.结构工程师，2011，27(5):111－115.