一类带干扰的离散风险模型①

陈奕含，杨 璐，张 拓，卜晓明，杨忻怡，王志福

(渤海大学数理学院，辽宁 锦州121000)

0 引 言

保险公司在实际生活中除了保险业务外，相当大一部分资金是由投资获得的，所以考虑了投资因素的风险模型对保险公司而言无疑是非常有意义的，对这一方面的研究也更有利于保险公司对自身前景预测和发展的安排.同时利率的影响也是经济中不可忽视的，本文在经典风险模型的基础上，考虑了投资收益也将利率因素的影响加以研究将其进行了推广得到了一个新的风险模型，同时得到和经典模型十分相似的破产概率的表达式以及Lundberg 不等式.

1 模型引入

设保险公司的盈余过程为

(1)u=U(0)为保险公司的初始资本，c ＞0是保险公司在单位时间内收到的保费，i 为常数，是利率;

(2)N(n)服从参数是(n，p)的二项序列，是理赔次数的过程，Xk，k=1，2，…表示每次的理赔额，是非负独立分布，它的分布函数是F(x)，E(Zk)=μ ＜∞;

(3)N1(n)服从参数是(n，p1)的二项序列，Yj，j=1，2，…是随机收益次数过程，表示每次的随机收益额，独立同分布，它的分布函数为G(y)，E(Yj)=γ ＜∞;

(4)假设N(n)，N1(n)，Zk，k=1，2，…，Yj，j=1，2，…，相互独立.记T=inf{n，U(n)＜0}为破产时刻，则Ψ(u)=P(T ＜∞)为发生破产的概率，若存在任意的n ＞0，U(n)≥0，约定T=∞.保险公司要保证自身的稳定经营，则在单位时间内，投资收益和保险费应该大于保险的索赔额，于是c(1+i)+p1γ－pμ ＞0.

2 主要结果

引理1 n ≥0 时{V(n)}具有平稳的独立增量

引理2 E［V(n)］=［c(1+i)+p1γ－pμ］n ＞0

引理3 存在r ＞0，使得E［e－rV(n)］＜∞由以上性质知可得:

定理1 方程E［r－V(1)］=1 存在正解R，则R为调节系数.

证明: 令g(r)=E［r－V(1)］－1，则可知g(r)是连续的函数，且得g(1)=0，g′(1)=－c(1+i)，则一定存在R ＞1 使得g(R)=0，即E［r－V(1)］=1.R 称为调节系数.为了的到破产概率Ψ(u)的表达式，需知:

引理4 若R 为一常数，且E［R－V(1)］=1，则{R－U(n)，n ≥0}为一正鞅.

证明 令An=σ{U(k)，k ≤n}是σ 代数，U(n+1)=U(n)－W(n+1)，其中W(n+1)=V(n+1)－V(n)与{U(0)，U(1)，…，U(n)}独立，与V(1)同分布，对任意自然数n，R－U(n)＞0，根据引理2 得

故{R－U(n)，n ≥0}为一正鞅.

定理2 初始准备金为的破产概率为

其中R 为调节系数，且Ψ(u)≤e－Ru(1+i)

证明: 根据引理1 可得{V(n)，n ≥0}具有平稳独立增量，且E(V(1))=c(1+i)+p1γ－pμ＜∞，所以，由强大数定律知∞，则，对任意n ≥0，因为破产时刻T是停时，则T ∧n 也为停时，又有引理4，由停时定理得

在上式中令n →∞，再由单调收敛定理和Lebesgue 控制收敛定理知

则

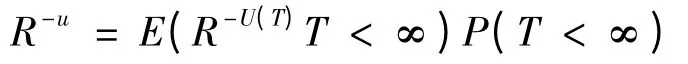
即

其中Ψ(u)≤e－Ru(1+i)，称为Lundberg 不等式，e－Ru(1+i)称为Ψ(u)的Lundberg 上界.

推论1 Ψ(u)≤R－u

推论3 存在正常数X，使得Ψ(u)～Xe－Ru(1+i)，u →∞

即

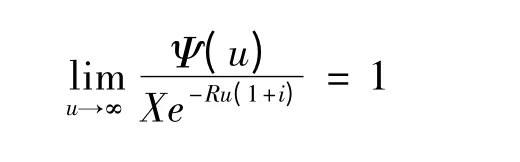
［1］ Gerber H U，成世学，严颖译.数学风险论导引［M］.北京:世界图书出版社，1997.

［2］ 于文广.干扰条件下的一个破产模型［J］.江南大学学报:自然科学版，2008，7(1):118－221.

［3］ 王晶刚，刘再明，周永卫.保险系统中一类双险种风险模型的破产概率［J］.数学理论与应用，2005，25(1):40－43.

［4］ 张相虎，赵明清.带干扰的双二项风险模型的破产概率［J］.经济数学，2005，22(4):351－355.

［5］ 成世学，伍彪.完全离散的经典风险模型［J］.运筹学学报，1998，2(3):42－54.

［6］ 孙立娟，顾岚.离散时间保险风险模型的破产问题［J］.应用概率统计，2002，8:293－299.

［7］ 方世祖，罗建华.双复合poisson 风险模型［J］.纯粹数学与应用数学，2006，6:271－277.

［8］ 张志德.一类随机保费风险模型下的破产概率［D］.上海:华东师范大学，2007.

［9］ 乔克林，何树红，马乐荣.考虑投资收益率随机变化的复合二项风险模型的破产概率［J］.延安大学学报(自然科学版)，2002，12:13－19.

［10］ 方世祖，张春梅，王志攀.带干扰的多险种离散风险模型的破产概率［J］.广西大学学报(自然科学版)，2007，32(3):282－284.

［11］ Kallenberg O.Foundations of Modern Probability［M］.New York:Springer，2006.