单重休假M/PH/1 排队系统驱动流模型研究①

毛炳蔚，赵 海，王福伟

(1.燕山大学理学院，河北 秦皇岛066004;2.燕山大学信息与科学工程学院，河北 秦皇岛066004)

0 引 言

近年来，很多工作集中于研究若干简单排队系统驱动的流模型［1～2］，这时，流模型的随机环境是某个排队系统的平稳队长过程.徐秀丽等研究了M/PH/1 排队系统驱动流模型［3］.在此基础上，我们引入休假策略，将模型推广为单重休假M/PH/1排队系统驱动流模型.休假策略的引入将使流模型的优化设计更为灵活多变.

1 二维驱动系统—单重休假M/PH/1 排队系统

考虑单重休假M/PH/1 排队系统，其到达间隔服从参数为λ 的指数分布，服务时间服从PH 分布，其m 阶表示为(α，T)，且αm+1=0，Te+T0=0，其中e 和I 分别表示相应阶数的分量皆为1 是列向量和单位矩阵，由此易知αe =1 及服务时间的均值为μ－1=－αT－1e.服务员遵循单重休假策略，即当系统为空时，服务员进行一次休假，当休假结束时，系统中有顾客则进入忙期，否则进入闲期.休假时间服从参数为θ 的指数分布，另外，到达间隔、服务时间及休假时间相互独立，服务顺序为先到先服务.令L(t)，J(t)分别表示时刻t 系统中的顾客数和服务员所处的状态，其中J(t)取－1，0，j(1 ≤j≤m)分别表示服务员处于假期、闲期和忙期中的位相状态j.

易知(L(t)，J(t))为拟生灭过程，其状态空间为Ω={(00)}∪{(k，－1)，(k ≥0)}∪{(kj)，(k ≥1，1 ≤j ≤m)}.将状态按字典顺序排列，可得其生成元为

令(L(t)，J(t))的平稳分布为

2 三维流模型—单重休假M/PH/1排队系统驱动流模型

令X(t)表示时刻t 流模型系统中的库存量，流体的净输入率取决于驱动系统的状态，当驱动系统处于闲期、假期且无顾客、假期且有顾客及忙期时，流体的净输入率分别为σ，σ1，σ2及σ3，其中σ＜0，σ1，σ2，σ3＞0，于是流模型过程为三维马氏过程(L(t)，J(t)，X(t))，且其平均漂移为

当d ＜0 且ρ ＜1 时，流模型为稳定系统.我们假设这一条件恒成立.此时，其稳态随机向量记为(L，J，X)，其中X 称为稳态库存水平，其稳态联合分布记为Fkj(x)=P{L=k，J=j，X ≤x}，((kj)∈Ω).引入向量F(x)=(F0(x)，F1(x)，F2(x)，…)，其中F0(x)=(F0，－1(x)，F00(x))，Fk(x)=(Fk，－1(x)，Fk1(x)，…，Fkm(x))，k=1，2，….不难得到流模型的稳态联合分布满足如下的矩阵微分方程

其中F(0)=(0，a，0，0，…，0)，Λ=diag(σ1，σ，Σ，Σ，…)，Σ=diag(σ2，σ3Im)

记F(x)、Fk(x)的Laplace 变换(LT)分别为，对微分方程(1)两边取LT，并考虑到边界条件F(0)，得

在此，引入一重要的矩阵二次方程

这个方程的最小非负解称为率函数矩阵.

引理1 若ρ ＜1，则二次矩阵方程(3)有最小非负解

其中

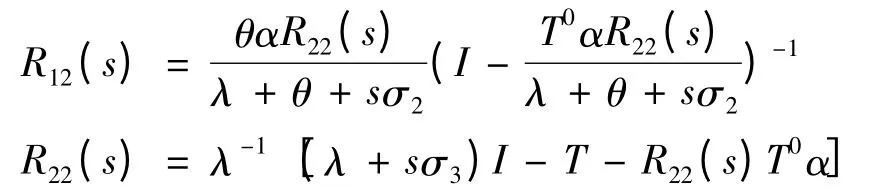
证明: 因矩阵B，A－sΣ 和C 都是上三角阵，故满足方程(3)的解必定也是上三角阵，故设

代入方程(3)，给出R(s)的元素所满足的方程组

由前二式得到R11(s)，R22(s)，代入第三式得到R12(s).证毕.

定理1 当流模型稳定(即d ＜0 且ρ ＜1)时，其稳态联合分布函数序列的}为

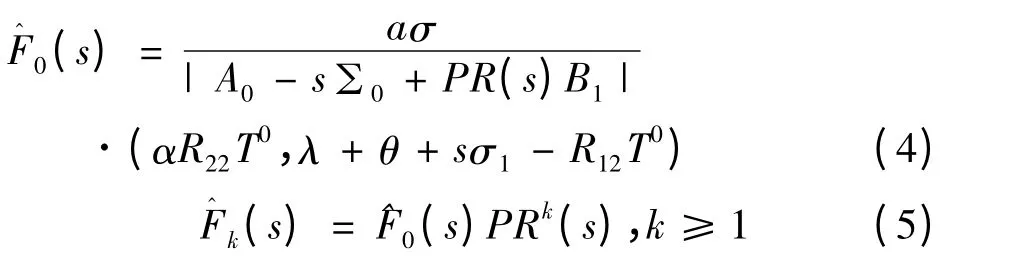
证明: 方程(2)可写为下列等价的差分方程组

若d ＜0 且ρ ＜1，三维Markov 过程(L(t)，J(t)，X(t))有唯一的平稳概率分布，从而上述差分方程组存在唯一解.于是，我们只需验证(4)和(5)满足上述方程组.

首先对k ≥2，将(5)代入方程组中的最后一式，得到

其次，将(5)代入方程组中的第二式得

最后，将(5)代入方程组中的第一式，得

经过简单计算证得(4).

3 库存量的稳态分布LT 及空库概率

两个特例

(1)当θ →∞时，模型退化为经典无休假M/PH/1 排队系统驱动流模型，此时空库概率为

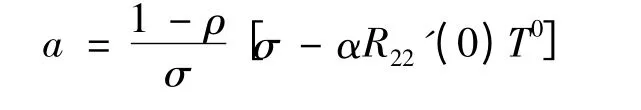
结论与文献［3］中的一致.

(2)当m=1 时，模型退化为单重休假M/M/1排队系统驱动流模型.此时，α=1，T=－μ，T0=μ，模型的空库概率为

［1］ J.Virtamo，I.Norros.Fluid Queue Driven by an M/M/1 Queue［J］.Queueing Systems，1994，16(3－4):373–386.

［2］ Q.L.Li，L.M.Liu，W.X.Shang.Heavy－tailed Asymptotics for a Fluid Model Driven by an M/G/1 Queue［J］.Performance Evaluation，2008，65(3－4):227–240.

［3］ Xiuli Xu，Yongze Zhao，Jie Geng，etc.Analysis of the Fluid Model Driven by an M/PH/1 Queue［J］.Journal of Information＆Computational Science，2013，10(11):3489－3496.