无穷区间上一类分数阶微分方程初值问题解的存在性①

李珊珊

(中国矿业大学(北京)理学院，北京100083)

1 预备知识

本文主要研究以下分数阶微分方程初值问题

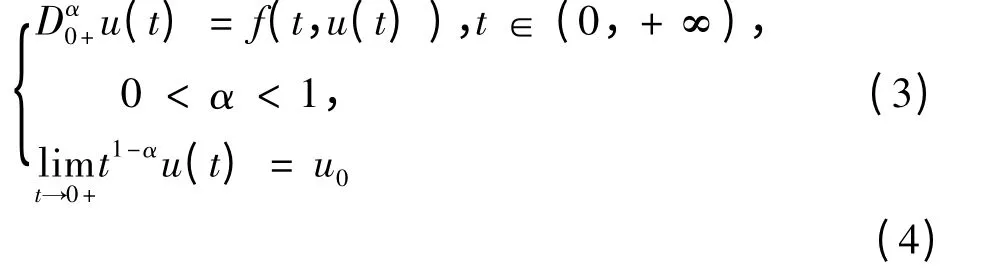
有关Riemann－Liouville 分数阶微积分定义及相关性质，参考文献［1］中69－90 页.本文中令R+=［0，+∞)，C1－α(R+)={x(t)|x:(0，+∞)→R，t1－αx(t)∈C(R+)}.

定义空间:

空间X 上的范数是:

空间Y 上的范数是:

引理1.1:(X，‖·‖X)，(Y，‖·‖Y)是Banach 空间.

这个引理的证明方法参见苏［2］中引理2.2 及寇［5］中引理3.1.

引理1.2:Z ⊆Y 且Z 是有界集，则Z 在Y 是相对紧集，只需满足以下两个条件:

这个引理的证明方法参见苏［2］中引理2.3.

2 主要结果

定理2.1: 假设函数f ∈(0，+∞)×R×R→R 且f ∈C1－α(R+)，存在非负有界函数a(t)，b(t)，c(t)∈L1(0，+∞)，使得

并且

则方程(1)，(2)至少存在一个解u(t)∈C1－α(R+).

证明: 我们熟知，方程(1)，(2)等价于积分方程:

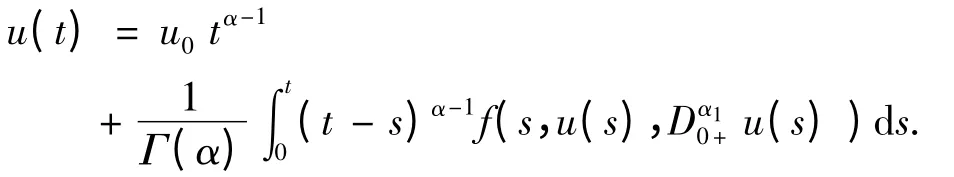
定义算子:

则方程的解转化为算子A 的不动点问题.

第一步:取

令U={u(t)∈Y:‖u‖Y≤R，则A:U →U.

事实上，

因为

故

所以

所以‖Au‖Y≤R，且根据Au(t)的定义，易知

即Au(t)∈Y，所以A:U →U.

第二步:利用引理1.2 证明对于∀V ⊂U，AV相对紧.

令I ⊂［0，+∞)且为紧区间，∀t1，t2∈I，不失一般性，设t1≤t2，则对∀u(t)∈V，

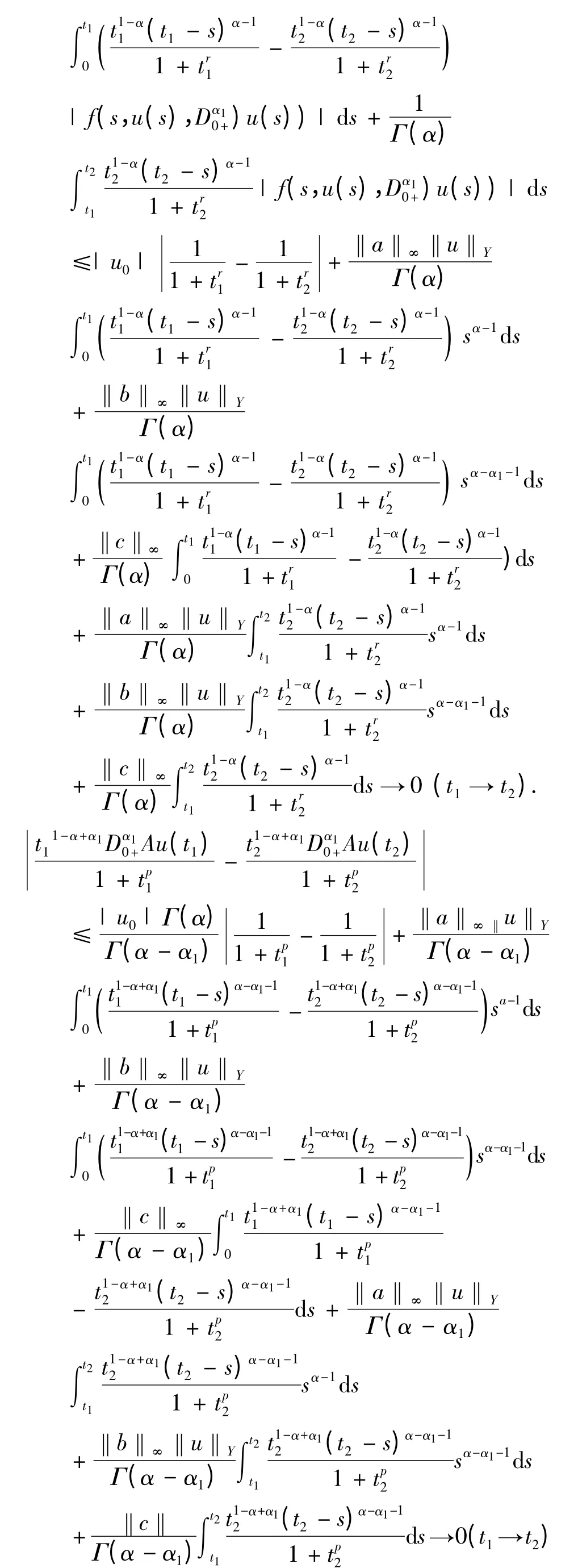
综上，由引理1.2 知，AV 是相对紧的.

第三步:A:U →U 是连续算子.

所以由Lebesgue 控制收敛定理知，A 是连续算子.

综上所述:由Schauder 不动点定理，方程(1)(2)至少存在一个解u(t)∈C1－α(R+).

［1］ A.A.Kilbas，H.M.Strivastava，J.J.Trujillo.Theory and Applications of Fractional Differential Equations［M］.Amsterdam:Elsevier，2006.

［2］ X.Su，S.Zhang.Unbounded Solutions to a Boundary Value Problems of Fractional Order on the Half－line［J］.Computer and Mathematics with Applications，2011，61(4):1079－1087.

［3］ J.Deng，Z.Deng.Existence of Solutions of Initial Value Problems for Nonlinear Fractional Differential Equations［J］.Applied Mathematics Letters，2014，32:6－12.

［4］ 刘玉记.无限区间上多分数阶微分方程初值问题解的存在与唯一性［J］.中国科学:数学，2012，42(7):735－756.

［5］ C.Kou，H.Zhou，Y.Yan.Existence of Solutions of Initial Value Problems for Nonlinear Fractional Differential Equations on the Half－axis［J］.Nonlinear Analysis，2011，74(17):5975－5986.