考虑轴压力影响的钢梁－剪力墙节点性能研究①

吴 铭

(上海建工，上海201199)

0 引 言

地震作用对高层建筑结构有着巨大的威胁，因此如何提高高层建筑结构的抗震性能成为了各国专家学者研究的重要课题.钢－混凝土组合结构结合了钢结构自重小，构件尺寸小，施工周期短以及混凝土结构整体刚度大，稳定性强，抗火性强和耐久性好等优点，成为结构体系的发展方向之一.在抵抗地震作用的过程中，节点区域是破坏的多发区域，控制和延缓节点区域的破坏能有效提高高层建筑的抗倒塌性能.因此，研究节点的受力性能、破坏机理，将其设计的传力明确、计算准确、构造合理对工程设计具有重要的指导意义.

Alan H.Mattoock 和G.H.Gaafar［1］在研究钢梁埋入钢筋混凝土柱作为支架或腋时［2］，使用的实际应力分布和模型分析时使用的应力－应变假定，因为钢梁是作为支架或腋使用的，在剪力作用点处传递的剪力是主要的，弯矩和水平轴力则可忽略不计.虽然在将剪力向柱边简化时，柱边有弯矩，但这一弯矩(Mn=Vn×a)与剪力有固定对应关系，不具有一般性.此外，他们在实验中在混凝土构件的顶部施加了一个均布的压应力，但在研究分析中却未考虑此均布荷载对构件节点的受力性能的影响.

1 弯剪相关性分析的简化模型与假定

当混凝土剪力墙顶部有轴向力且剪力作用处同时存在较大弯矩时，如果直接套用已有公式而不考虑轴向力与弯矩的影响［3］是不合理的.因为轴向力与弯矩的存在会降低节点的抗剪承载力.

图1 是I 形截面钢梁埋入钢筋混凝土节点实际应力分布和假定的应力及应变分布.与下翼缘下侧及上侧相接触的混凝土受压区分别称为下侧前受压区与下侧后受压区，其所受合力分别记为Cdf和Cdb;距钢筋混凝土构件边缘的距离分别记为xdf和xdb;有效宽度则记为bedf和bedb.与上翼缘下侧及上侧相接触的混凝土受压区则分别称为上侧前受压区与上侧后受压区，其所受合力分别记为Cuf和Cuf;距钢筋混凝土构件边缘的距离分别记为xuf和xuf，有效宽度则分别记为beuf和beub.下侧后受压区和上侧后受压区和称为后受压区，下侧前受压区和上侧前受压区合称为前受压区.

为进行内力简化，可假定极限状态下，混凝土剪力墙边缘压应变为0.003，前受压区用等效矩形应力块来代替曲线应力分布，等效矩形应力块的均布应力为0.85fc，形状系数为β1;后受压区混凝土受压时采用rusch 应力－应变曲线;Cuf=kfCdf，Cdb=kbCub且xdb=xdf，xuf=xdf.

1.1 平衡方程的建立

混凝土下侧前受压区与上侧前受压区的合力大小分别为:

式中，fc为混凝土轴心抗压强度;β1为受压区高度与实际受压区高度的比值，根据文献［4］取为0.8;c 为前受压区高度;bedf为前受压区有效承压宽度;σ 为剪力墙上均布压应力.

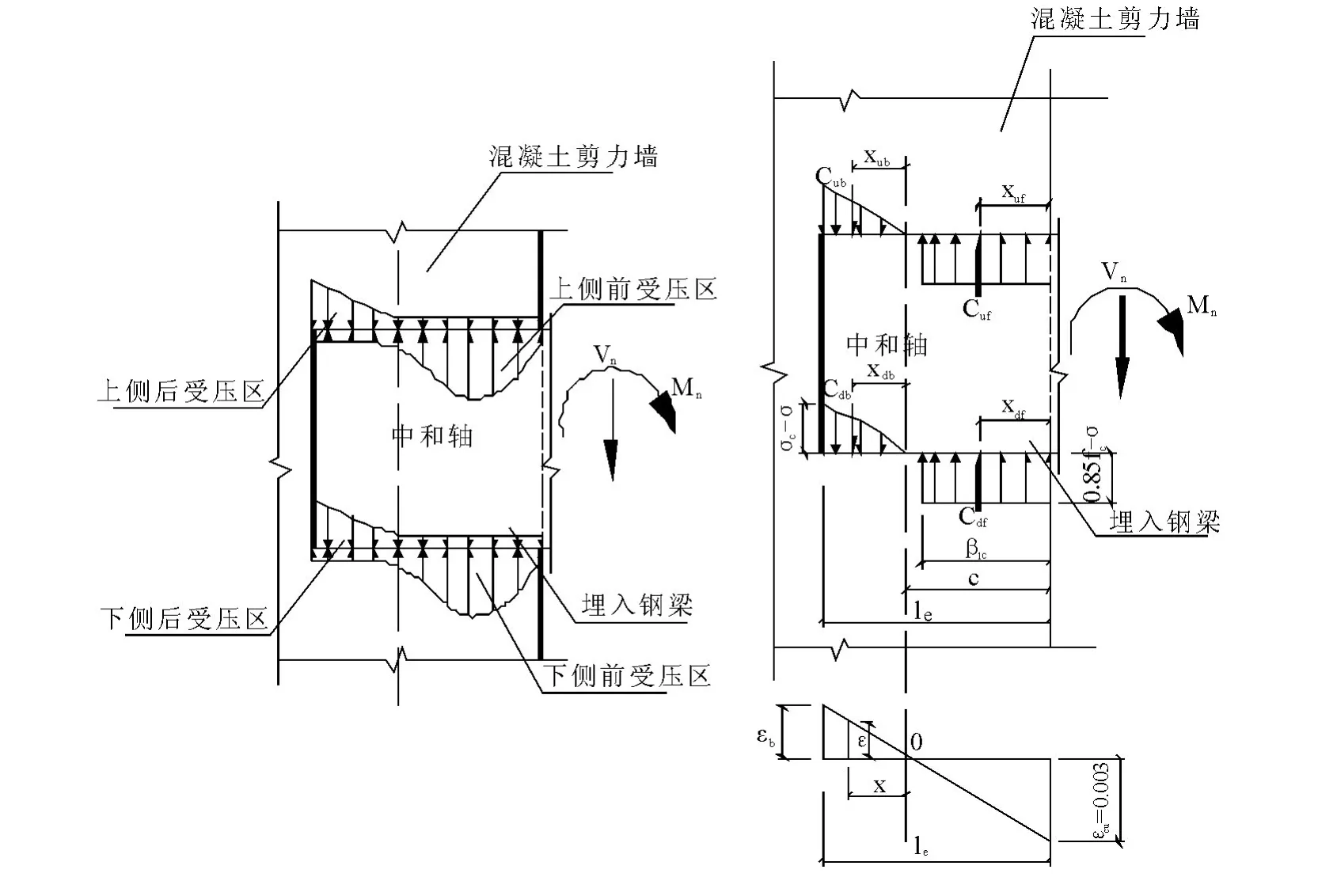
图1 I 型截面钢梁埋入钢筋混凝土节点实际应力分布(左)和假定的应力及应变分布(右)

假定应变线性分布，从应变为0 处开始对下侧后受压区积分，可得其的合力为:

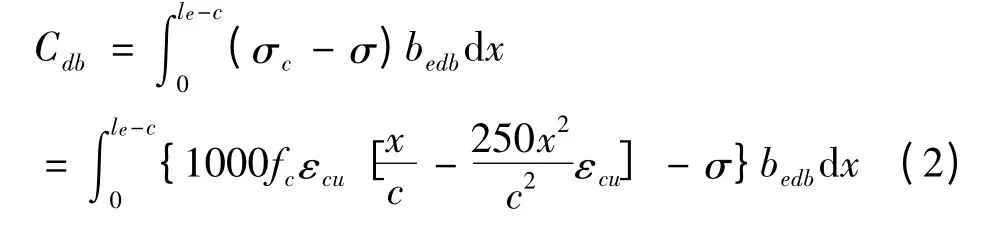
积分后受压区的抛物线内力和合力对O 点取矩，在εcu=0.003，E=3.0×104N/mm2时，以C30的混凝土强度推导σ=0.3fc时的，可得后下侧后受压区到中和轴的距离为:

根据竖直方向力的平衡，可得:

对下翼缘下侧与混凝土剪力墙边缘处取矩，根据弯矩平衡，可得:

通常，在kf，kb已知的情况下，上面两个方程有三个未知数Vn，Mn，c 无法求解.

1.2 钢梁埋入钢筋混凝土构件的弯剪相关性

令k 为前受压区高度系数，且:

将相关各式带入平衡方程(公式4)和(公式5)进一步整理，并对k 求导，可得:

我们知道，在节点处，剪力的存在会降低节点的抗弯承载力，反之亦然.由上面的分析可知，节点所能承受的最大剪力和弯矩是通过一个参数联系起来的，而且k=c/le＞0 时，剪力与弯矩成反比，剪力的增长会降低弯矩的承载力.

事实上，在上面求解方程时只要(1+kb)bedb与(1+kf)bedf近似相等，就可以将这两组参数消去，从而达到化简方程的目的，实际上并不需要kf=kb和bedf=bedb同时成立.

1.3 承压破坏的理论弯剪相关曲线

当(1+kb)bedb与(1+kf)bedf近似相等时:

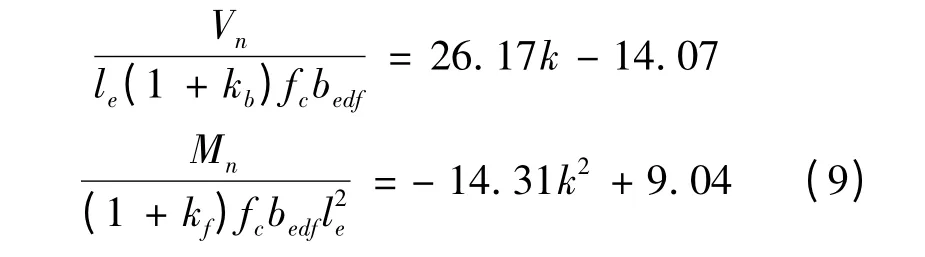
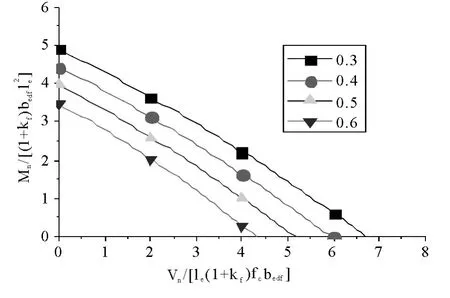
图2 混凝土强度为C30 时弯剪相关曲线

需要说明的是，随着钢梁在混凝土剪力墙中le的增大，会使得混凝土在后受压区的受力情况发生变化，以致不能符合假设的情况，因此，在后续章节中对计算弯剪相关性曲线的参数le进行修订.并将梁高做为有效埋入长度le的一个修正参数来引入.

2 有限元模拟

2.1 有限元模型

采用通用有限元软件ABAQUS 对节点进行非线性有限元分析，并与以往文献试验结果进行对比验证.模型中混凝土及钢梁采用实体单元，钢筋采用桁架单元.混凝土剪力墙和钢梁及钢筋的变形协调分别通过接触单元及嵌入单元来实现.模型考虑了钢连梁与混凝土之间的粘结滑移效应.试件SCB－ST 的有限元模型如图3 所示.试验为空间双向加载，模拟时将双向加载简化为单向加载进行有限元分析，以提高分析效率.

图3 试件有限元模型

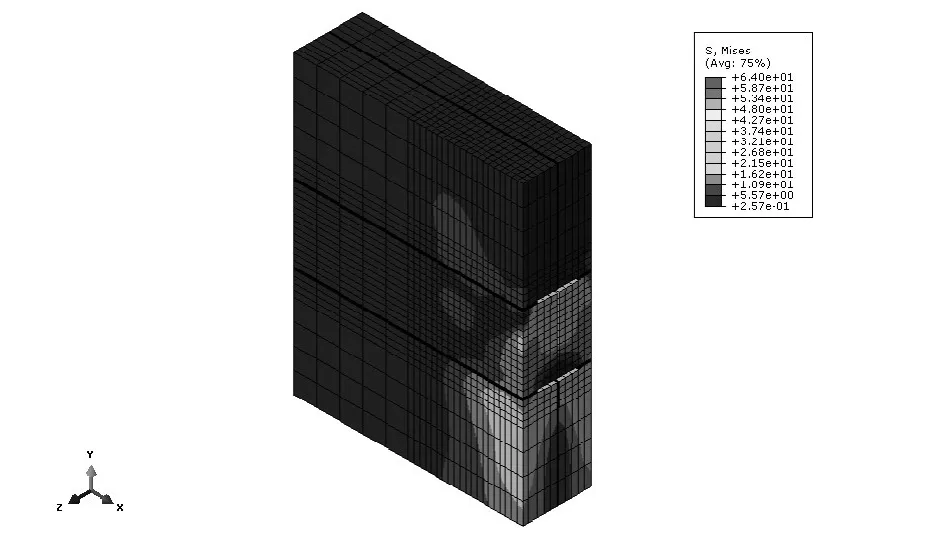
图4 剪力墙von Mises 应力分布

图5 有限元计算与试验结果对比

材料本构模型选取如下:钢材和钢筋采用带von Mises 屈服面的经典弹塑性本构模型.混凝土受压和受拉时采用塑性损伤模型.

边界条件设置如下:将剪力墙底部节点3 个方向的自由度固定，墙体压应力通过直接施加在墙顶刚性加载垫块上的集中力来模拟，再在钢梁上施加向下的位移约束.

计算时打开大位移开关以考虑集合非线性.

2.2 结果验证

图4 为有限元模拟的试件SCB－ST 节点破坏时混凝土的von Mises 应力分布，图5 为有限元计算的转角－荷载曲线与试验结果的对比.从图5 可以看出，在加载初期，有限元模拟的曲线与文献曲线误差较大，但在加载后期有限元模拟曲线与试验曲线吻合良好，说明模型可以准确地模拟节点受力情况.

3 改变参数的数值模拟

3.1 钢梁埋入长度对节点承载能力的影响

本节建立T1 组模型来研究钢梁埋入长度对节点受力性能的影响，其中混凝土剪力墙高1700mm，长1500mm，宽500mm，轴压比取0.3，强度取为C30;钢梁埋入长度从300mm 增加到1000mm，梁截面梁高400mm，腹板厚10mm，翼缘宽220mm，厚12mm.

图6 剪力墙墙边钢梁截面弯矩－转角曲线

得到的节点在不同埋入长度时剪力墙墙边钢梁截面弯矩－转角曲线如图6 所示.由图6、图7可知，其它条件不变，当钢梁长度从300mm 增大到700mm 时节点承载力提高较大，而从800mm 增大到1000mm 时节点承载力提高明显降低，只是在剪力墙边缘混凝土破坏后，提供了更多的内部混凝土继续承压，而延缓了节点的破坏.钢梁长度小于700mm 且转角大约为0.02rad 时，节点承载力达到峰值，之后逐渐下降，因此对于T1 模型，700mm 左右的埋入长度是比较合适的.在计算节点强度时，钢梁的埋入长度有时不应取钢梁的实际埋入长度，为了保证混凝土剪力墙能够对钢梁提供足够的约束，同时保证埋入部分的钢梁能全部发生作用，通过对已有文献试件埋入深度和破坏情况分析，参照对T1 组埋入长度的分析，取:

其中，是混凝土剪力墙与钢梁接触部分提供的截面惯性矩，是钢梁的截面惯性矩，为混凝土弹性模量，为钢梁弹性模量.经运算化简后可得:

当按上面提供的有效埋入长度大于实际埋入长度时，对于节点承载能力的计算，应该采用实际埋入长度计算.当按上面公式得到的有效埋入长度小于实际实际埋入长度时，节点承载能力的计算应该采用按上面公式计算得到的有效埋入深度，这样未充分发挥作用的钢梁埋入长度，可以作为安全储备，实现“强节点弱构件”.

表1 模型钢梁埋入深度比较

图7 不同埋深时上翼缘上侧混凝土应力曲线

在T1 组基础上改变梁高度和埋入长度，再建立T2，T3，T4 组模型如表1 所示.将各参数的影响列于表中，通过对比不同钢梁高度下钢梁埋入长度对承载力的影响，可以发现梁高对承载力有一定影响，这时采用代入公式计算节点承载力，避免了过大的钢梁埋入长度造成计算结果偏大的情况，使计算结果更加接近真实情况.事实上仅有文献8 中计算的埋入长度超过了本文的计算有效埋入长度，说明大多数已有研究都未充分考虑埋入长度的合理范围，也就意味着节点承载能还有很大的提高空间.

3.2 混凝土剪力墙轴压比对节点承载能力的影响

本节使用T1 组模型，调整钢梁埋入长度取500mm，600mm，700mm，混凝土剪力墙的轴压比取0.3，0.4，0.5，0.6，0.7.得到节点在不同钢梁长度和轴压比的情况下，不同钢梁长度时承载力－轴压比曲线如图8 所示.

从图中可看出:随着轴压比的增大，节点的延性明显降低，且轴压比的增大使得节点承载力在达到极限承载能力之后更加迅速的降低.由于轴压比的增大也造成钢梁上下翼缘受压区域的混凝土提早破坏，使节点在达到极限承载能力后承载力迅速降低.

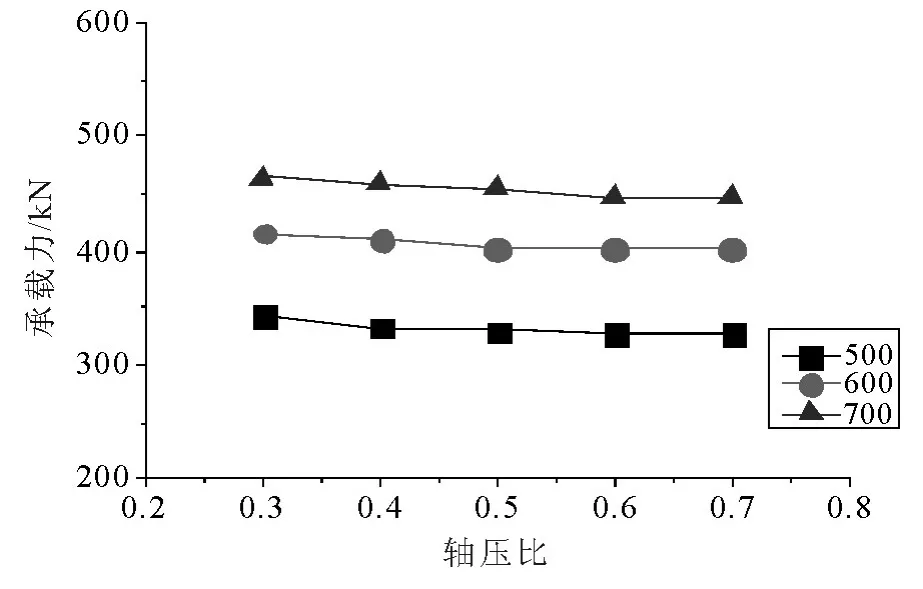
图8 不同钢梁长度时承载力－轴压比曲线

通过图9 可以发现:对于相同的加载点竖向位移，当轴压比增大时钢梁的拔出长度也会增大，再通过参照图中不同轴压比下拔出长度－荷载曲线，可以得出随轴压比增大钢梁更易被拔出，这是由于随轴压比的增大，钢梁上下翼缘前受压区靠近剪力墙边缘的混凝土更易受到受压破坏，减小了混凝土与钢梁间的摩擦力.

图9 加载点竖向位移－拔出长度图

3.3 钢梁弯剪组合对节点承载能力的影响

本节使用T1 组模型钢梁埋入剪力墙的长度取为600mm，加载点位置分别取为500mm，1000mm，1500mm，2000mm，2500mm.得到的节点在不同弯剪组合情况下节点达到极限承载能力时的弯剪值如表2 所示.

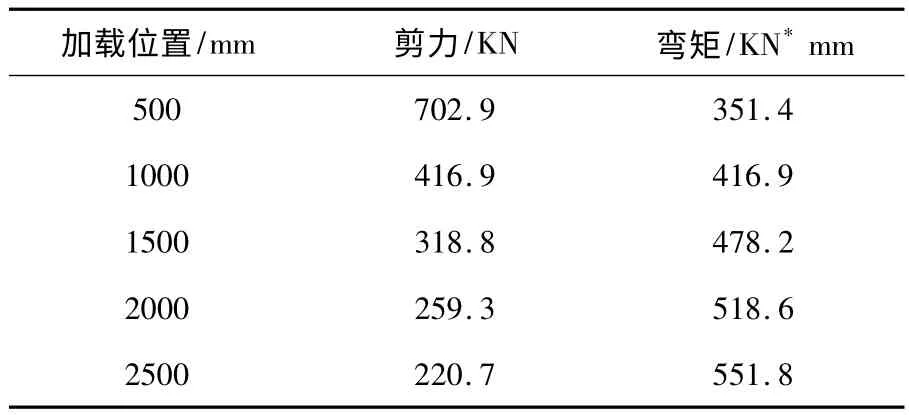
表2 节点达到极限承载能力时的弯剪值

通过表2 可以发现随着加载点位置远离剪力墙，节点承载能力达到极限时所能承受的弯矩不断增大，同时剪力不断减小.可见弯矩和剪力的存在共同影响了节点的承载能力，弯矩和剪力之间的负相关性也印证了前面的弯剪相关性公式.

4 结 论

在有限元分析的基础上，分析了钢梁埋入长度、剪力墙轴压比对节点承载能力的影响，给出了剪力墙节点区域混凝土发生破坏时弯剪相关性中的有关参数的取值情况.

本文的主要结论如下:

(1)通过理论分析，给出了不同轴压比和混凝土强度下，钢梁埋入钢筋混凝土剪力墙节点的弯剪相关性理论公式和曲线.

(2)通过对模型的有限元分析，明确了轴压比地增大节会造成点延性的降低.

(3)提出钢梁有效埋入长度的计算公式并通过有限元分析钢梁有效埋入长度公式的合理性.

(4)有限元软件ABAQUS 对节点模型进行非线性数值模拟具有较高的精度，模型能够准确地预测节点的破坏模式和承载力状况.

［1］ Mattock AH，Gaafar GH.Strength of Embedded Steel Sections as Brackets.ACI Journal，1982，79(9):83－93.

［2］ 高利人.钢梁一混凝土柱组合框架结构在国外的发展［J］.建筑结构，2002，32(5):34－37.

［3］ Wan－Shin Park，Hyun－Do Yun.Panel Shear Strength of Steel Coupling Beam－Wall Connections in a Hybrid Wall System.Journal of Constructional Steel Research，2006，62:1026－1038.

［4］ 顾祥林.混凝土结构基本原理［M］.上海:同济大学出版社，2004.

［5］ 周军海.钢梁埋入长度对钢—砼组合连梁与砼剪力墙节点承载力影响的试验研究与分析［D］.长沙:中南大学，2007.

［6］ 戴卓.钢—砼组合连梁与砼剪力墙节点承载力的试验研究与分析［D］.长沙:中南大学，2008.

［7］ 朱辉.钢连梁与混凝土剪力墙节点承载力试验研究与分析［D］.长沙:中南大学，2008.

［8］ 陈康华.钢—砼组合连梁与砼剪力墙节点抗震性能试验研究［D］.长沙:中南大学，2008.