桩土动力相互作用简化方法对比研究①

毕常芸，徐 倩

(1.同济大学地下建筑与工程系，上海200092;2.济源职业技术学院，济源459000)

0 引 言

桩基础以其承载能力大、沉降小、稳定性好等特点而被广泛应用于高、大构筑物中，尤其是在软土地区.但是桩基础承受横向荷载能力较弱，在遇到地震等强烈横向荷载作用下，场地土体发生液化，桩基础就显得尤为脆弱.我国处于多震国家，地震区的分布相当广泛，然而在目前我国通常采用拟静力法来进行桩基础抗震设计的，这些建立在刚性地基假定上的规范，在小变形的情况下适用，对于罕遇地震作用下，土体进入非线性状态，变形大，结构－桩－土之间的相互影响也增大了，因此计算结果与实际情况相差较大，可能造成结构延性不足而倒塌.故而研究桩土动力相互作用有着重要的实际工程意义.

Novka［1，2］假定土体为薄土层且水平向无限延伸，结合Winkler 地基梁模型求解桩的刚度及动阻尼.Ngagar［3］在Kondner［4］所提出的非线性应力应变关系的基础上建立了非线性桩土相互作用模型.孔德森等［5］对经典的及改进的动力Winkler 模型进行了全面的对比分析，并提出了改进的动力Winkler 模型，该模型能更好的反应桩基动力阻抗随激振频率变化特征.燕斌［6］对比了不同简化模型在不同地震作用下结构的动力响应情况，并建议在抗震设计中应直接采用动力P－Y 曲线法.黄雨等［7］总结了国内外液化场地桩基抗震设计的现状，并指出各种简化设计方法存在的问题.张建民等［8］结合Penzien 模型，基于能准确描述场地液化前、后土体大变形的本构模型，建立桩－土地震相互作用计算模型，并分析计算了阪神地震中液化侧扩流的桩基.

国内外学者对桩土相互作用的研究很早就开始了，但是研究内容大多针对于计算模型的研究上，以模型不断优化为目的，模型计算较为复杂，并不能很好的运用到实际的工程设计中，导致设计计算时因为采用了不适用的简化计算方法，而产生计算复杂、工作量大、精度不够等问题.因此本文选用目前最为常用的4 种简化计算方法进行对比研究，并结合工程上的6 种工况，将简化计算模型计算结果与有限元模拟结果对比，分析简化模型计算结果的误差，并分析其适用性，得到的结果能对实际的工程设计选用计算方法提供依据.

1 桩土动力相互作用简化方法

通常简化模型主要包括4 部分:上部结构、承台、桩以及等效为桩土相互作用的土弹簧.

1.1 底部直接嵌固分析模型

底部直接嵌固分析模型是将桩基础与承台地面连接做固接处理，并以此对结构进行抗震分析.将得到的最不利内力作用在承台底部，利用m 法对桩基础进行地震响应计算.

此方法是基于刚性基础的假定，并未将桩土相互作用考虑在内，被我国桥梁规范采用.

图1 底部直接嵌固模型

1.2 集中土弹簧分析模型

集中土弹簧分析模型是将桩基础简化为集中土弹簧作用在承台底部，输入地震激励，然后对上部结构进行分析，得到最不利内力.将得到的结果再作用与承台底部，再对桩基础进行动力响应分析.其中m 法用于近似考虑桩土相互作用.

此方法计算量小，具有较强实用性，因而在工程上得到广泛运用.

图2 集中土弹簧分析模型

1.3 等效悬臂底部嵌固分析模型

等效悬臂底部嵌固分析模型是将一定深度处的桩按固结处理，计算其地震响应.根据经验嵌固深度通常采用3 到5 倍桩径.

此方法考虑了桩和土对上部结构的影响以及桩土之间的相互作用，并且计算量小，是进行桩土动力相互作用研究中常用的简化计算方法之一.

图3 等效悬臂底部嵌固分析模型

1.4 分布弹簧分析模型

分布弹簧分析模型是将桩与土之间的相互作用简化为连续分布且相互独立的弹簧，然后对上部结构以及桩基础进行地震响应分析.

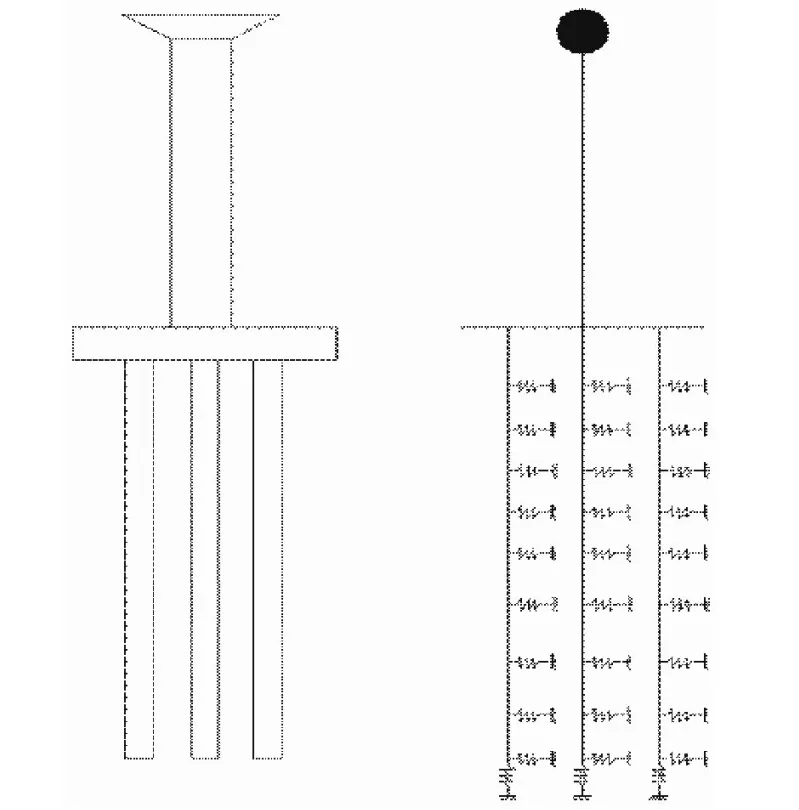
图4 分布弹簧分析模型

与之前的三种方法相比，该法考虑了土－桩－上部结构三者的共同作用，使计算结果更为准确，但计算耗时长，收敛过于复杂.

2 简化计算模型对比研究

2.1 模型概况

选取文献［9］中的模型［9］进行研究，简化结构如图5 所示.该结构为3×1 群桩基础，将上部结构简化成为置于墩顶的集中质点，桩和墩与承台刚接，其几何性质和物理性质分别见表见表1 及表2.

图5 简化结构示意图

表1 结构几何性质

表2 结构物理性质

2.2 工况设定

本文共设定了7 种研究方法，如表3 所示.其中探讨了不同嵌固深度对等效嵌固法计算精度的影响，以及确定分布弹簧刚度的不同方法对分布弹簧模型进行研究.

表3 桩土动力相互作用简化分析方法

本文选择砂土作为研究土体，共分为6 种工况进行分析，其基本概况如表4 所示.场地类型基本参数如表5 所示.地震波选用EL－Centro 地震波.

表4 分析工况基本概况

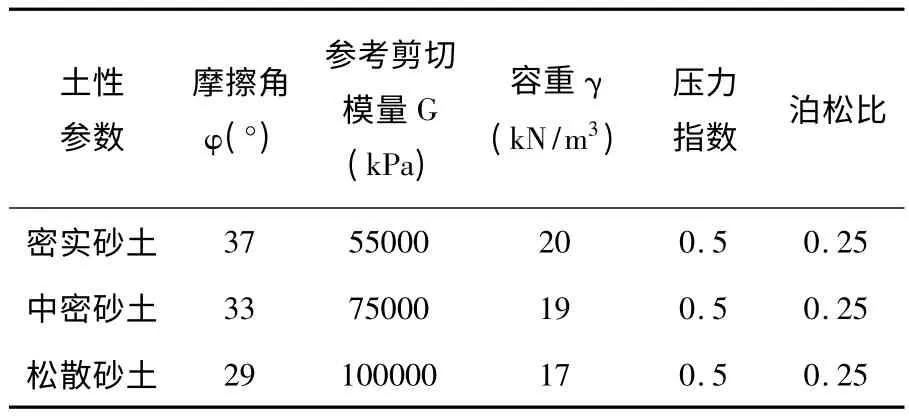
表5 砂土基本参数

2.3 模型分析与评述

2.3.1 直接嵌固分析模型

将运用底部直接嵌固分析模型计算的结构地震相应的结果与有限元模拟的结果对比，6 种不同工况下的计算结果如图6 所示.从图中可以发现，模型在密实多遇地震作用下误差最小，近100%，在松砂罕遇地震作用下误差最大，近250%.由此可知运用底部直接嵌固模型分析结构动力响应时，误差较大，因此不宜用于抗震分析中.

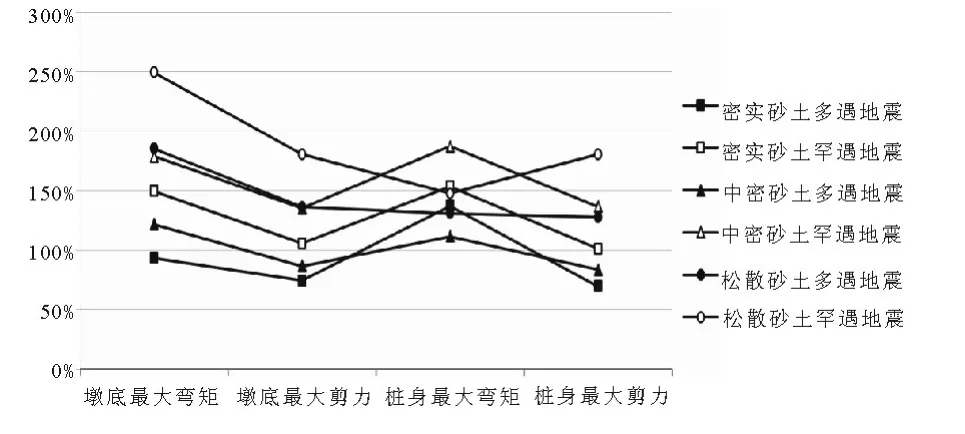
图6 直接嵌固模型结构地震响应计算误差百分比

2.3.2 集中土弹簧分析模型

由图7 中可以看出，松散砂土罕遇地震作用下，误差最大，约160%，密实砂土多遇地震作用及中密砂土多遇地震作用下，误差最小，约80%.从图中可以看出，该分析模型用于墩底最大剪力及桩身最大剪力时误差相对较小，尤其在计算密实和中密砂土多遇地震作用下，在50%以内.因此，此分析模型勉强适用于密实和中密砂土多遇地震作用下的桩基抗震分析.

2.3.3 等效嵌固分析模型

针对不同嵌固深度的等效模型，分别为3D 等效嵌固分析模型、5D 等效嵌固分析模型对6 种不同工况作用下的结构地震响应进行研究，误差计算结果如图8 所示.通过总体比较三种不同嵌固深度模型的误差可以发现，随着嵌固深度的不断增加，计算结果与有限元模拟结果的误差也在不断的减小.5D 分析模型的误差最小，在20%～160%范围内.

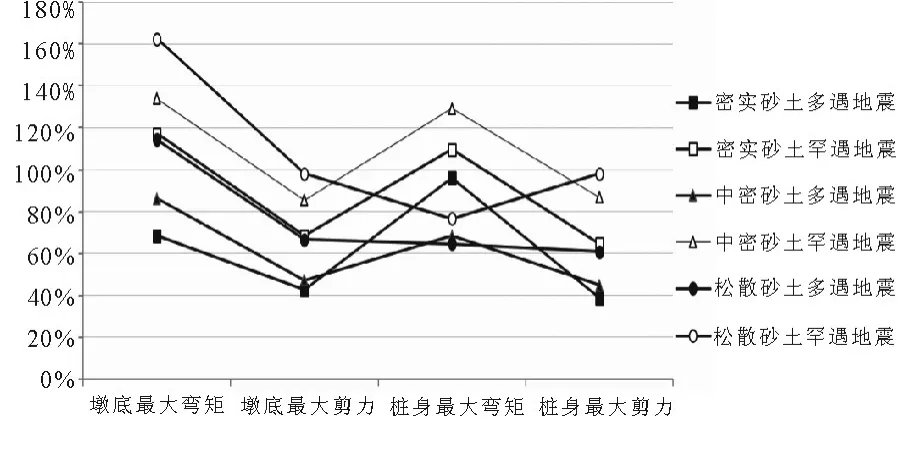
图7 集中土弹簧模型结构地震响应计算误差百分比

图8 等效嵌固模型结构地震响应计算误差百分比

3D 等效嵌固模型仅有密实砂土及中密砂土在多遇地震作用下能满足工程精度的要求，其他几种工况下误差仍较大.因此3D 等效嵌固模型运用还是有相当大的局限性的.

对5D 等效嵌固模型进行详细分析，墩底最大弯矩的误差较大，在40%～160%范围内.墩底最大剪力及桩身最大剪力的计算效果较好，除松散砂土在罕遇地震作用下这一工况外，其余误差均在15%～60%范围内.另外密实砂土在多遇及罕遇地震下、中密砂土在多遇地震下结构地震响应的误差在80%以内.因此5D 等效嵌固模型适用于计算除松散砂土在罕遇地震作用下的其他工况的墩底最大剪力及桩身最大剪力的计算以及密实砂土在多遇及罕遇地震下、中密砂土在多遇地震下这三种工况的结构动力响应.

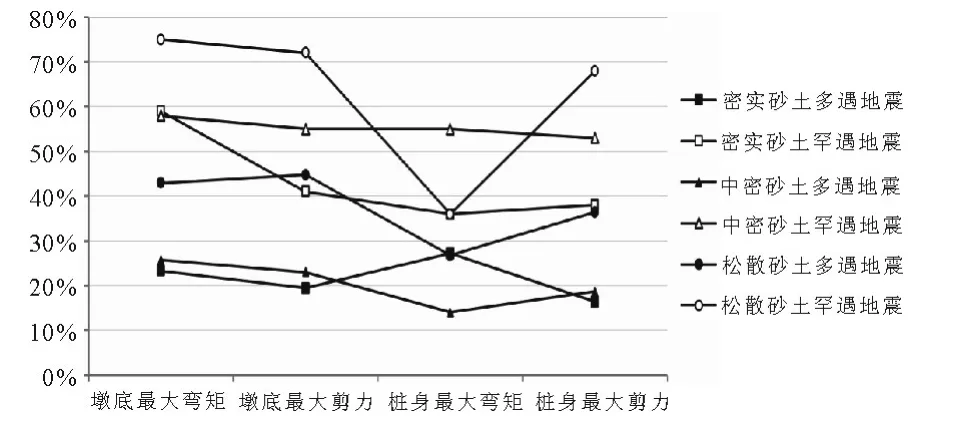
图9 m 法分布弹簧模型结构地震响应计算误差百分比

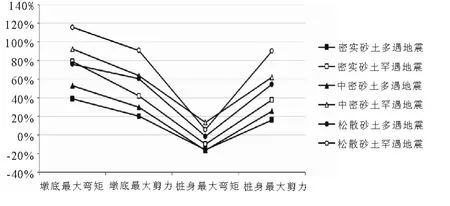
图10 修正m 法分布弹簧模型结构地震响应计算误差百分比

图11 修正p－y 曲线法分布弹簧模型结构地震响应计算误差百分比

表6 各简化方法适用工况

2.3.4 m 法分布弹簧分析模型

从图中可以看出多遇地震作用下，中密砂土及密实砂土中结构动力响应的误差较小，所有结构地震响应误差均在30%以内.从整体上看，罕遇地震作用下结构动力响应的误差要明显高于多遇地震作用下计算结果的误差，因此可以证明，m 法不适用于土体变形较大的情况下桩基抗震响应研究

由此可以得出，在多遇地震作用下进行结构地震响应研究时，m 法能满足工程的精度要求，尤其是对中密及密实砂土中的结构.

2.3.5 修正m 法分布弹簧分析模型

在对6 种不同工况下结构动力响应的研究中可以发现，密实砂土多遇地震作用下误差较小，均小于40%.对响应情况研究，墩底最大弯矩误差普遍较大，在40%～120%范围内.桩身最大弯矩误差较小，中密砂土罕遇地震作用下误差最大，约为18%.

需要注意的是，在误差分析中，多遇地震及密实砂土罕遇地震作用下，桩身最大弯矩的误差在－20%至18%的范围内，出现了负值，说明使用修正m 法计算的桩身弯矩偏小，因此在设计中应给予桩身弯矩适当的提高.

经分析，修正m 法分布弹簧模型能适用于多遇地震情况下，计算误差能满足工程精度要求.

2.3.6 修正p－y 曲线法分布弹簧分析模型

对结构动力响应计算结果分析发现，运用修正p－y 曲线法能达到较高的精度，6 种工况下的误差均在25%以内.其中松散砂土在罕遇地震作用下结构地震响应误差最小.墩底最大弯矩，墩底最大剪力，桩身最大剪力误差在5%－25%范围内.

因此，修正p－y 曲线法分布弹簧分析模型适用于各种工况，但需要对桩身最大弯矩做一定调整.

3 结 论

对比各种简化计算方法，集中土弹簧模型和5D 等效嵌固模型较其余集中模型误差较小，适用于部分工，且满足工程的精度要求.对于分布弹簧分析模型能较好的进行桩基抗震分析.m 法适用于变形较小的情况，修正p－y 曲线分布弹簧模型的计算结果精度更高，适用性更广.但要注意在运用这两种模型时，桩身最大弯矩计算结果偏小，设计偏不安全，因此要对桩身最大弯矩进行适当调整.

各简化方法适用工况见表6.

［1］ Novak M.Dynamic Stiffness and Damping of Piles［J］.Canadian Geotechnical Journal，1974，11(4):574－598.

［2］ Novak M.Vertical Vibration of Floating Piles［J］.Journal of Engineering Mechanics Division，ASCE，1977，103(1):153－168.

［3］ Naggar E I，Novak M.Nonlinear Model for Dynamic Axial Pile Response［J］.Journal of Geotechnical Engineering，ASCE，1994，120(2):308－329.

［4］ Kondner R L.Hyperbolic Stress Strain Response:Cohesive Soils［J］.Journal of the Soil Mechanics and Foundation Engineering Division，ASCE，1963:89－96.

［5］ 孔德森，栾茂田，杨庆.桩土相互作用分析中的动力Winkler模型研究评述［J］.世界地震工程，2005，21(1):12－17.

［6］ 燕斌.桥梁桩基础抗震简化模型比较研究［D］.上海:同济大学，2007.

［7］ 黄雨，八嶋厚，张锋.液化场地桩－土－结构动力相互作用的有限元分析［J］.岩土工程学报，2005，27(6):646－651.

［8］ 张建民.水平地基液化后大变形对桩基础的影响［J］.建筑结构学报，2001，22(5):75－77.

［9］ 王青桥.桥梁桩基础抗震设计方法比较研究［D］.上海:同济大学，2009.