基于EFDC的长江常州段污水排江浓度场数值模拟

潘炜

(江苏省环境保护厅，江苏 南京 210036)



·环境预警·

基于EFDC的长江常州段污水排江浓度场数值模拟

潘炜

(江苏省环境保护厅，江苏 南京 210036)

长江感潮河段水流与污染排放引起的浓度场复杂多变，基于EFDC(Environmental Fluid Dynamic Code)模型，采用正交曲线网格拟合自然河道边界，建立了长江常州段的水动力和水质模型。采用现场同步实测资料，与计算结果比对，证明该模型在水动力和水质两个方面都与实测数据吻合较好，满足了实际工程的需要；同时由于长江水流运动较快，一阶降解动力学已经满足了化学需氧量(COD)、氨氮(NH3-N)和总磷(TP)浓度计算要求，可以不考虑它们复杂的生化反应过程。

EFDC；感潮河段；水流；污水排放；浓度

常州市北枕长江，东扼太湖，地处太湖流域，是中国经济发展最快的地区之一。由于太湖地区排污的严格限制和太湖流域河网纳污能力有限，常州产生的部分污水不得不排入长江常州段。

长江常州段属长江下游感潮河段，潮汐为非正规半日浅海潮，每天2次涨潮和落潮，平均潮周期为12 h 26 min，潮波明显变形，落潮历时大大超过涨潮历时，平均涨潮历时约3 h 41 min，落潮平均历时约8 h 45 min，该江段在部分时间会发生双向流动，因此污水排放后浓度变化规律极为复杂。

虽然国内对部分情况下中、小型河道的污染物浓度计算规定了解析公式[1]，但这些计算公式显然不能运用于长江常州段这种河道自然岸边界曲折，水面宽阔，水流往复，水底地形变化不定，且伴有潮汐作用的河道污染物浓度场计算。同时长江常州段区域中有多个重要的居民生活用水取水口，在这一区域设置城市污水处理厂尾水排放口必须非常慎重，保证其不会对这些取水口水质产生影响。因此，必须采用数值模拟的方法对尾水排江产生的污染物浓度场进行计算。

EFDC(Environmental Fluid Dynamic Code)是由美国环保署资助开发的地表水数值模型，EFDC是综合水环境数学模型，其包括水动力、水质、拉格朗日粒子、波浪和毒物等多种计算模块，可以计算盐度、温度、营养物、泥沙和重金属等各种水环境因子。其中EFDC的水质模块可以计算C、N、P、O和Si等各元素不同形态的物质在不同水动力条件下的分布。它可以用于模拟河流、河口、湖泊、水库以及近海多种地表水体。它在美国、欧洲得到了广泛的运用[2-3]，在中国的珠江、长江武汉段、巢湖等水体也有一定运用[4-8]，但是，较少见到EFDC模型在长江感潮河段下水质的计算模拟。笔者基于EFDC模型，对长江常州段的流场进行了计算模拟，与实际测量结果对比吻合较好，该模型反映了该江段潮汐流场和浓度场的实际变化情况。

1 数学模型

为了适应复杂的长江常州段自然河道岸边界，以得到更好的计算结果，EFDC计算的网格使用正交曲线网格。

1.1 控制方程

在正交曲线坐标下，二维水深平均方程如下。

连续方程：

(1)

式中：H——水位；u、v——正交曲线坐标下ξ、η2个方向的水深平均流速的分量；m1、m2——2个方向正交曲线坐标的拉梅系数，m=m1·m2；χ——水位。

动量方程：

(2)

(3)

式中：H——总水深；g——重力加速度；f——科里奥力系数；C——谢才系数；τηξ、τξη、τξξ和τηη——粘滞应力项，它们在正交曲线网格下由下式计算。

(4)

式中：υt——平面涡粘性系数，在EFDC中可以选择为常数或者用Smagorinsky湍流理论计算[9]。为了计算污水处理厂尾水排放造成的影响，还必须考虑污染物的输运和降解过程，其计算方程如下。

(5)

式中：C——污染物浓度；K——污染物降解系数；S——污染物的源项；Aξ、Aη——污染物在ξ、η2个方向的污染物混合系数。

1.2 定解条件

由于该段长江是潮汐河道，所以上、下游的水流边界条件采用水位边界条件。同时在这2个边界上的污染物浓度都给定浓度随时间变化的值，即：

χ(ξ,η,t)|Γ1=χ1(ξ,η,t)

χ(ξ,η,t)|Γ2=χ2(ξ,η,t)

C(ξ,η,t)|Γ1=C1(ξ,η,t)

C(ξ,η,t)|Γ2=C2(ξ,η,t)

(6)

式中：Γ1、Γ2——上、下游的边界。在固壁上采用无滑移条件及物质通量为零的条件。初始条件对计算结果的影响不会很大，采用实测值给定即可。EFDC中的模型采用交错网格，算子分裂法求解，具体可见文献[9]。

2 计算条件设置

2.1 计算区域与网格划分

该研究范围上起于常州魏村闸，下止于江阴水文站，总长约34.5 km，基本包括了长江常州段的全部区域。其中重点区域是常州录安州下游，常州城市污水处理厂尾水排放口附近。图1是计算区域网格图与监测点位布置概况。其中S1、S2是水质监测站位；T1是24h潮位监测站，污水处理厂的尾水排放口也在这个位置；P1、P2和P3是定点水流监测点，P2和P3还同步监测了水质。

整个计算区域共有网格29 700个，网格尺度范围为10～200 m。从图1可以看到，正交曲线计算网格贴合地非常好。在排污口位置附近，T1点的附近进行了加密以获得更精确的结果。所有数据的监测都为2014年2月23日8时—2014年2月24日13时。

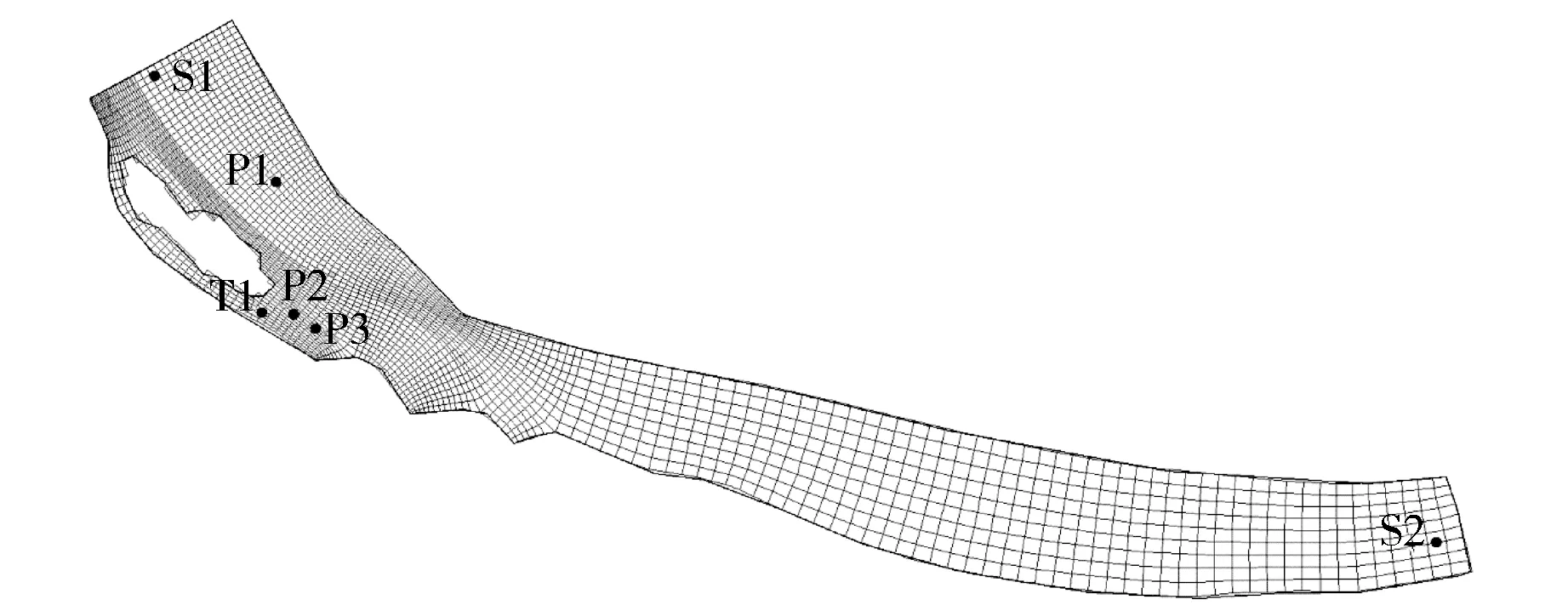
图1 计算区域网格图与监测点

2.2 边界条件与参数

计算用的潮位边界采用常州魏村闸潮位站和江阴水文站的长江小潮实测资料；上、下游的水质分别采用S1、S2的实测数据；污水排放口的流量和水质数据采用实测数据。

该研究主要计算高锰酸盐指数(CODMn)、氨氮(NH3-N)和总磷(TP)。虽然NH3-N和TP的生物化学反应复杂，但是，考虑到长江水流运动速度比较大，水质点从上游到下游所经历的时间不超过24 h，绝大多数的生物化学反应在如此短时间内难以产生实际效果，因此，用一阶反应动力学去模拟CODMn、NH3-N和TP是适当的。根据前人在相关区域的研究成果，并用该次实测数据和计算结果对模型参数进行率定，这3种物质在本区域的降解系数分别为：KCODMn=0.15 d-1，KNH3-N=0.1 d-1，KTP=0.06 d-1；糙率取值为0.020～0.025；计算的时间步长为10 s[10-12]。

3 计算结果比较与讨论

3.1 流速潮位比较

图2是T1点24 h潮位比较的结果，其潮位实测频率为2次/h，每5 min输出一个结果。

如图2所示，潮位的计算结果与实测结果吻合良好，平均误差仅为5 mm，最大误差也仅为8 mm，误差较大区域出现在潮位最低处，该区域呈现出明显的非正规半日潮特征，其涨潮时间比落潮时间短很多，这与江阴潮位站实测结果相符。

图3—5是P1、P2和P3点的垂向平均流速和流向的比较结果。

如图3—5所示，P1、P2和P3点流速、流向计算值与实际观测值总体吻合良好，其中流速的最大相对误差和平均相对误差分别为12.8%和8.3%。

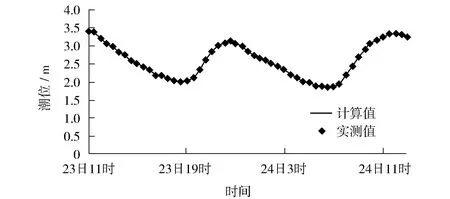
图2 T1点潮位比较

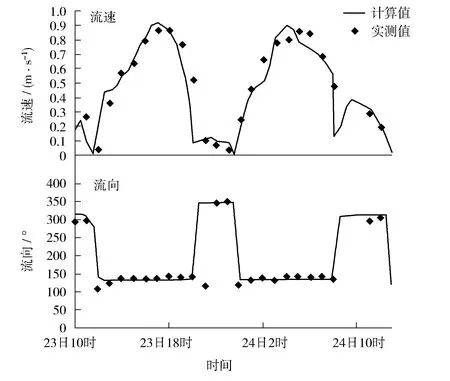
图3 P1点流速与流向结果的比较

图4 P2点流速与流向结果的比较

从上面的结果可以发现，EFDC的计算结果无论是在潮位还是在流速与流向上，其与实测值都吻合良好。这证明了EFDC所使用的二维正交曲线网格下的平均水深模型能够很好地模拟长江常州段在潮汐作用下的水动力情况。

图5 P3点流速与流向结果的比较

3.2 水质比较

为了研究EFDC的水质模型对潮汐河段的适用性，该研究在该计算区域设置了P2和P3两个水流水质同步监测点。图6—8是这两个点的COD、NH3-N和TP的实测值和计算值的比较结果。

图6 CODMn计算值与实测值比较

从图6—8中可以看出，虽然CODMn、NH3-N和TP的数值计算结果和实测结果都很接近，但是，相较而言，CODMn和TP的精度较好，其平均误差分别为8.1%和8.5%，而NH3-N的精度稍差，平均误差为13.1%。

图9-11分别是尾水排入长江常州段后，在涨憩和落憩时刻CODMn、NH3-N和TP的浓度增量图。

图7 NH3-N计算值与实测值比较

图8 TP计算值与实测值比较

从图9—11中可以看到，长江常州段感潮河段，有明显的涨落潮运动。同时，虽然不同污染物的源强不同，但是，受到同样的水动力的影响，它们的浓度增量分布的区域和形状是类似的。在涨潮时，污染物主要沿夹江向上游输运，对外江区域基本不产生影响；落潮时，污染带横向分布的尺度明显宽于涨潮情况，但其平均浓度则相对较低。

从上述计算结果的精度可以知道，EFDC采用二维水深平均模型不但能够成功地计算长江潮汐河段的水流运动与污染物浓度范围分布，而且 CODMn、NH3-N和TP浓度的模拟采用一阶降解动力学计算的已经能得到能够满足精度要求的结果。这主要是因为长江的流速非常大，污染物经过整个计算区域的时间很短，因此，在如此短的停留时间内，多数复杂的生化反应的效应是很小的，可以不需要考虑这些反应。

图9 涨落潮CODMn浓度增量

图10 涨落潮NH3-N浓度增量

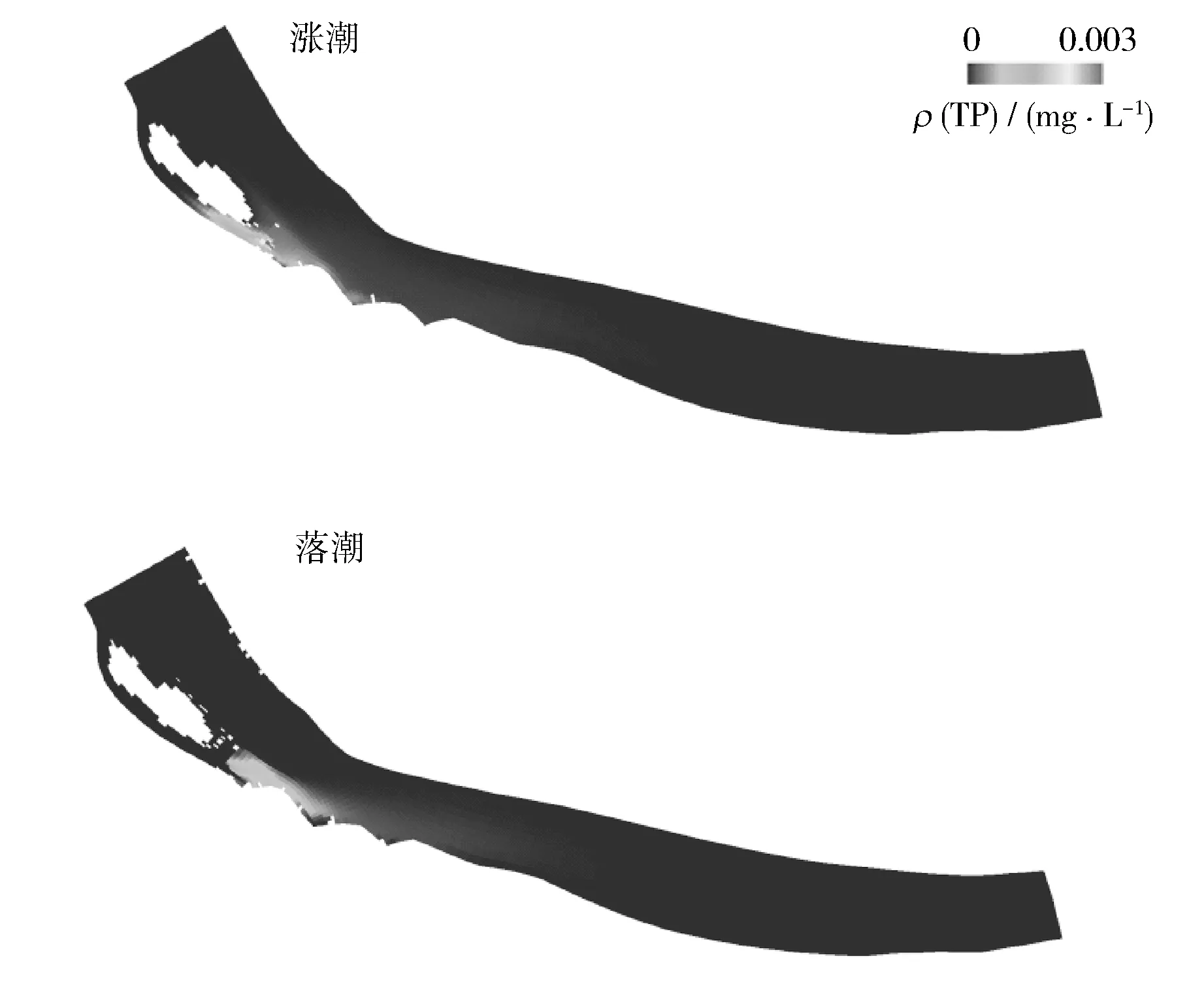
图11 涨落潮TP浓度增量

4 结论

笔者使用EFDC模型建立长江常州感潮河段的二维水深平均模型，对常州的城市污水处理厂尾水排放的情况进行了计算。结果表明，二维模型的精度令人满意，能够满足感潮河段实际工程流场与浓度场模拟计算的要求。

对CODMn、NH3-N和TP的生化过程采用一级降解动力学进行简化。与实测资料的对比发现，由于江段流速较快，对于长江常州段而言，简单的一级降解动力学已经足够满足工程的需求，可以不考虑它们复杂的生化反应。

[1] GB/T 25173-2010 水域纳污能力计算规程[S].

[2] KANG J R, HAMRICK J H,TISDALE T. Application of three-dimensional hydrodynamic model for Lake Okeechobee[J]. J.Hydraul.Eng.,2000,126:758-771.

[3] JUNTAO Z,FALCONER R A,BINLIANG L. Refinements to the EFDC model for predicting the hydro-environmental impacts of a barrage across the Severn Estuary[J]. Renewable Energy,2014,62:490-505.

[4] 李彤，李适宇.广州珠江感潮河网水流泥沙数值模拟[J].中山大学学报:自然科学版, 2012, 51(5):14-20.

[5] 齐珺,杨志峰,熊明,等.长江水系武汉段水动力过程三维数值模拟[J].水动力学研究与进展:A辑,2008,23(2):212-218.

[6] 华祖林,刘晓东,褚克坚,等.基于边界拟合下的水流与污染物质输运数值模拟[M].北京：科学出版社,2013:181-212.

[7] 李一平,唐春燕,余钟波.大型浅水湖泊水动力模型不确定性和敏感性分析[J].水科学进展, 2012,23(2)：271-277.

[8] GU Z W, ZONG X X. Prediction of algal blooming using EFDC model:case study in the Daoxiang Lake[J].Ecological Modelling,2011,222:1245-1252.

[9] Tetra Technologies Inc. The environmental fluid dynamics code theory and computation volume 1:hydrodynamics and mass transport[R]. 2007:1-33.

[10] 吴建兰,李熙,陈秀梅.实验室率定法测算长江南通段污染物降解系数[J].四川环境, 2012,31(5):36-40.

[11] 邱巍.长江口竹园排污区COD降解系数的测试与分析[J].上海水利,1996(4):33-36.

[12] 胡四一,施勇,王银堂,等.长江中下游河湖洪水演进的数值模拟[J].水科学进展,2002,13(3):278-286.

Numerical Simulation on Pollutants Concentration Field in Changzhou Reach of Yangtze River by EFDC Model

PAN Wei

(JiangsuEnvironmentalProtectionDepartment,Nanjing,Jiangsu210036,China)

The concentration field caused by discharged pollutant were complex in the tidal reach of the Yangtze River.By the use of orthogonal curvilinear grid fitting river natural border, the hydrodynamics and water quality model on Changzhou Reach of Yangtze River was built based on EFDC model. The comparison between observations and the results of calculation showed that both the hydrodynamics model and the water quality model agreed with the observations well, and the model could satisfied practical engineering. Because of the large velocity of Yangtze River, the first order decrease mechanics was good enough to calculate the concentrations of COD, NH3-N and TP, and the more complex ecological reaction would not be considered.

EFDC; Tidal river; Water flow; Wastewater discharge; Concentration

2014-09-22；

2014-11-03

潘炜(1976—)，女，工程师，硕士，从事环境管理研究工作。

X522

A

1674-6732(2015)01-0005-05