纯电动汽车经济性换挡规律仿真研究*

江 昊，赵 韩，黄 康，刘拂晓

(合肥工业大学机械与汽车工程学院，合肥 230009)



2015142

纯电动汽车经济性换挡规律仿真研究*

江 昊，赵 韩，黄 康，刘拂晓

(合肥工业大学机械与汽车工程学院，合肥 230009)

为提高纯电动汽车的续驶里程，降低能量消耗率，本文中针对其燃油经济性进行了换挡规律的仿真。首先制定出两参数静态经济性换挡规律；然后利用动态规划算法找出在ECE循环工况下的最优挡位，并据此对所制定的静态经济性换挡规律进行修正，得到最终经济性换挡规律曲线；最后，在UDDS行驶工况下，建立了纯电动汽车耗电量模型，对修正前后的换挡规律进行仿真。结果表明，修正后的换挡规律能有效地降低纯电动汽车的能量消耗率。

电动汽车；能量消耗率；静态经济性换挡规律；动态规划；耗电量模型

前言

机械式自动变速器(AMT)由于具有传动效率高、体积小、成本低、继承性好等优点，是各国各种纯电动车辆的理想传动形式[1-3]，并已逐渐在纯电动车辆上装备应用。纯电动客车一般采用3个挡位，而纯电动轿车则采用2个挡位。

经济性换挡规律是指自动变速器能够使汽车以较高的效率或较低的能量消耗率行驶而进行的换挡操作。由于电动汽车的驱动部件是电机，能源部件是电池，这与传统燃油汽车动力部件和能源部件均为发动机大为不同，因此，关于经济性换挡规律的制定方法有很大差异。目前，关于电动汽车AMT经济性换挡规律的研究文献较少。文献[1]中对纯电动汽车的经济性换挡规律进行了研究，但其制定的换挡规律仅考虑使电机工作效率最优，而未对整个驱动系统的工作效率进行研究。

本文中依据传统经济性换挡规律的制定方法制定出静态经济性换挡规律，然后结合典型的行驶工况，用动态规划算法制定出经济性换挡规律，仿真试验表明，此种换挡规律具有较优的能量消耗率。

1 电机工作特性

电动机作为纯电动汽车上唯一的动力源，其性能的好坏直接影响电动汽车的经济性和动力性。本文中采用上海电驱动公司生产的某款电动机作为研究对象。驱动电机的技术参数见表1。

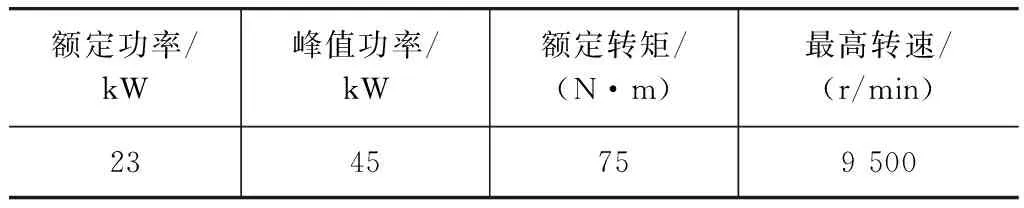
表1 驱动电机部分参数

由于本课题所设计的电动汽车中，加速踏板行程与驱动电机输出转矩线性相关，因此，仿照发动机负载特性曲线测定方法，得到驱动电机负载特性，见图1；同时测定的驱动电机效率曲线见图2。

2 静态经济性换挡规律的制定

所谓静态换挡规律是指，利用电机/发动机的稳态试验数据作为求解换挡规律的依据，从而制定的换挡规律[4]。

2.1 驱动电机效率方程

汽车的行驶方程[5]为

Ft=Ff+Fw+Fi+Fj

(1)

式中：Ft为车辆驱动力；Ff为滚动阻力；Fw为空气阻力；Fi为坡度阻力；Fj为加速阻力。

经理论推导展开得

(2)

(3)

式中：Ttq为驱动电机输出力矩；i0为主减速器传动比；ig为变速器传动比；ηt为传动效率；r为车轮滚动半径；f为滚动阻力系数；CD为风阻系数；A为车辆迎风面积；θ为道路坡度角；u为车速；δ为汽车旋转质量换算系数。

车速与驱动电机转速关系为

(4)

由式(2)～式(4)可以看出，驱动电机转矩是ig与n的函数，简记为

Ttq=f1(ig,n)

(5)

同时依据驱动电机转矩转速特性可知：

Ttq=f2(α,n)

(6)

式中：f2(·)为转矩插值函数；α为加速踏板行程与全程的比值，或称归一化加速踏板行程，以下简称加速踏板行程，0≤α≤1。

由驱动电机效率特性曲线可得

ηm=f3(Ttq,n)

(7)

式中f3(·)为效率插值函数。

联立式(4)、式(6)和式(7)得到电机效率与车速、挡位传动比与加速踏板行程的关系为

(8)

约束条件为

(9)

2.2 静态换挡规律的制定

静态经济性换挡规律制定的基本原则是尽可能使驱动电机工作在高效率区。结合式(8)可得换挡点的公式为

(10)

当α分别取0.1，0.2,…,1时，便可得到静态经济性升挡规律。例如当α取0.5时，1挡和2挡的效率曲线如图3所示。

通过合理选用降挡速差得到静态经济性换挡规律如图4所示。

3 静态经济性换挡规律的修正

对于电动汽车而言，静态换挡规律仅考虑了电机效率最优，而忽略了电池、变速器和逆变器的影响因素。因此，静态换挡规律不是电动汽车的最佳换挡规律。下面以动态规划算法对已经制定的静态经济性换挡规律进行修正。

动态规划技术的控制算法的基本思想是优化运行时纯电动汽车的动态特性。此外该优化是就时间范围而论，而不是关于随着时间推移的一个瞬间[6-8]。即该优化立论于整个行驶工况循环。

3.1 某一车速区域内加速踏板开度的确定

由式(7)可知，驱动电机的负载特性曲线是关于加速踏板行程α与电机转速n的插值函数。这一插值函数的数学表达式为

(11)

式中：Pα为在加速踏板行程为α时，电机运行于恒功率区域的功率；Pmax为峰值功率；Tα为加速踏板行程为α时，驱动电机运行于恒转矩区域内的转矩；Tmax为峰值转矩。

在匀速工况下，要求的加速踏板行程由式(12)确定：

(12)

式中：αT为驱动电机工作在恒转矩区域内，所要求的加速踏板行程；αP为驱动电机运行于恒功率区域内，所要求的加速踏板行程。Tneed可由式(5)确定；Pneed可由式(13)确定。

(13)

在加速工况下，要求的加速踏板行程由式(14)和式(15)确定：

(14)

(15)

式中：αT[0]为驱动电机工作在恒转矩区域时加速起始时刻所要求的加速踏板行程；αT[N]为在N时刻所要求的加速踏板行程；αP[0]为驱动电机工作在恒功率区域时加速起始时刻所要求的加速踏板行程；αP[N]为在N时刻所要求的加速踏板行程。

3.2 动态规划算法

对于给定的行驶循环(本文中采用ECE循环工况)，获得最佳经济性的优化运行策略，可以通过求解一个动态优化问题得出。这一动态优化问题构造过程如下[6-7]。

在时间的离散格式中，纯电动汽车电驱动的模型可表达为

x(k+1)=f[x(k),u(k)]

(16)

(17)

式中：u(k)为关于控制变量的矢量；u为车速；i为1挡或2挡传动比；x(k)为关于系统状态变量的矢量，它是控制变量u(k)的响应，x(k)=(T，ω)，其中T为电机转矩，ω为电机角速度。

系统的状态方程为

(18)

优化的目标是在ECE市内循环工况下，以最小的电耗为目标，求解优化的控制输入量u(k)。总电耗J被定义为一个价格函数，使之趋于最小。

(19)

其中

(20)

式中：ηm为电机效率，由式(8)、式(14)和式(15)决定；ηt为整车传动系效率，它为传动比的函数；M为行驶循环的持续时间；L为瞬时电耗率，它是系统状态x和输入u的函数；ηb为电池放电效率，是放电电流的函数；ηi为逆变器效率，它与逆变器输入电流相关。

依据试验数据拟合得到电池放电效率与逆变器转换效率分别为

ηb=3.48×10-5I2-2.43×10-2I+100

(21)

ηi=-5.69×10-7I4+1.14×10-4I3-

1.25I2+0.92I+69.6

(22)

对于电池放电电流I可依据式(23)进行求解：

UIηbηi=Pneed

(23)

式中U为电池端电压，由于在放电过程中，电压变化不大，故取定值。因此，每一时刻，对于式(20)的最小耗电量的求解，也可转化为求解式(23)的最小电池放电电流。

在式(20)求极小值的过程中，必须设置某些约束条件，以保证所有参数的变化处于有效范围内。约束条件为

0≤ωm≤ωm_max

(24)

Ttq_min≤Ttq≤Ttq_max

(25)

SOCmin≤SOC≤SOCmax

(26)

式中：ωm为电机角速度；SOC为峰值电源的荷电状态，它被约束在其底线和顶线电平范围内。

动态规划所需的计算量随状态变量数呈指数规律增长[6]。故驱动电机、传动装置的效率归结为具有寻址表的静态模型。

基于Bellman的优化原理，规划算法步骤如下。

M-1步：

(27)

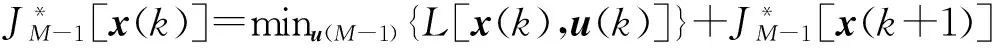
(28)

以上递归方程由M-1步到零步逆推求解。得到ECE工况下最优挡位信息，如图5所示。

3.3 静态经济性换挡规律的修正

虽然从上节得到了加速踏板行程与最优挡位信息，但由于数据量过小，不能很好地拟合成换挡曲线。因此，本文中通过修正静态换挡规律，使相同加速踏板行程下，修正后的换挡规律所对应的挡位能够尽量接近优化得到的最优挡位。具体步骤如下。

(1) 将3.1节确定的ECE循环工况所需加速踏板行程的信息带入所制定的静态经济性换挡规律曲线中，得到对应的挡位，如图6所示。

(2) 比较图5和图6，以最优挡位为目标，通过修正静态换挡规律曲线下的不同加速踏板行程下的换挡阈值，使新的换挡曲线在不同加速踏板行程下对应的挡位接近最优挡位，最终得到的换挡规律曲线如图7所示。

对比图7与图4可以看出，修正后的换挡规律曲线明显较静态换挡规律曲线在换挡速度方面提前。这是因为在低速区域，由于2挡所需的电机转矩比1挡大，故2挡状态下的电池放电电流大于1挡状态下的放电电流，从而导致2挡状态下的逆变器的效率远大于1挡状态下的逆变器效率，并且此时逆变器的效率影响因子较大，最终导致修正后的换挡曲线的换挡速度小于静态换挡曲线。而在高速区域，则电机的效率处于主导地位，电池放电效率与逆变器效率差别不大。另一方面，无论是低速区域还是高速区域，电池放电效率影响因子较小，低于逆变器效率与电机效率的影响因子。故而在开发纯电动汽车时，应重点考虑逆变器的效率与电机的效率。

4 动态换挡规律效果验证

4.1 耗电量仿真模型的建立

在交通运输中，一般以kW·h/km度量车辆单位行驶距离所消耗的能量。对于配置蓄电池的电动汽车，以kW·h为单位度量在蓄电池输出端所测定的原始能量消耗更为适宜。

能量消耗是蓄电池输出端功率积分的过程，它应与汽车阻力功率、传动装置损耗功率、电动机驱动损耗功率和电子仪器设备损耗功率之和相平衡[9]。

利用Matlab/Simulink分别建立驾驶员模型、换挡逻辑模型、电池模型、驱动电机模型和车辆动力学模型等，整体模型如图8所示。

4.2 UDDS耗电量验证

在所有的实际交通环境中，很难精确而定量地描述牵引力和车速的变化，但某些代表性的行驶循环已被开发用以模拟典型的交通环境。依据国家标准关于电动汽车的续驶里程与能量消耗率试验方法，采用的是ECE循环工况，本文中作为优化的行驶工况也是ECE循环。因此，现用UDDS城市循环工况对所优化的经济性换挡规律进行验证。UDDS工况如图9所示。

在图8所示的耗电量模型中，以UDDS循环工况作为跟随车速，经模型运行仿真得到的静态经济性换挡规律电池SOC变化曲线与修正后的准静态经济性换挡规律电池SOC变化曲线如图10所示。

在UDDS循环工况下，静态经济性换挡规律所对应的100km耗电量为42.94kW/h，修正后的经济性换挡规律对应的100km耗电量为38.43kW/h，能量消耗率降低了10.5%。在ECE循环工况下，静态经济性换挡规律所对应的100km耗电量为19.32kW/h，修正后的经济性换挡规律对应的100km耗电量为18.26kW/h，能量消耗率降低了5.48%。

试验结果表明，修正后的经济性换挡曲线能够很好地降低汽车能量消耗率。

5 结论

(1) 以电机运行效率最优为目标建立了静态换挡规律。

(2) 以ECE工况为依据，以动态规划算法为手段，得到了最优挡位信息；以最优挡位信息为目标，修正了静态换挡规律。

(3) 在UDDS工况下验证修正前后的换挡规律，得到修正后的经济性换挡规律具有较优的能量消耗率，证明了此种方法制定出的经济性换挡规律具有理论的可行性与优越性。

[1] 秦大同,周保华.两挡电动汽车动力传动系统的参数设计[J].重庆大学学报,2011,34(1):1-6.

[2] 岳东鹏,王杰,张俊智.装配AMT的HEV动力总成协调控制策略[J].交通运输工程学报,2010,10(1):43-49.

[3] 胡建军,李康力,胡明辉.纯电动轿车AMT换挡过程协调匹配控制方法[J].中国公路学报,2012,25(1):152-158.

[4] 周学建,付主木,张文春,等.车辆自动变速器换挡规律的研究现状与展望[J].农业机械学报,2003,34(3):139-145.

[5] 余志生.汽车理论(第4版)[M].北京:机械工业出版社,2007.

[6] Lin C-C, Peng H, Grizzle J W, et al. Power Management Strategy for a Parallel Hybrid Electric Truck[J]. IEEE Transactions on Control System Technology,2003,11(6).

[7] Lin C-C, Kang J-M, Grizzle J W, et al. Energy Management Strategy for a Parallel Hybrid Electric Truck[C]. Proceedings of the American Control Conference, Arlington, VA, June 25-27,2001.

[8] Lin C-C, Peng H, Jeon S, et al. Control of a Parallel Hybrid Electric Truck Based on Driving Pattern Recognition[C]. Proceedings of the 2002 Advanced Vehicle Control Conference, Hiroshima, Japan, September,2001.

[9] Ehsani Mehrdad, Gao Yimin, Emadi Ali.现代电动汽车、混合动力电动汽车和燃料电池车——基本原理、理论和设计[M].倪光正,倪培宏,熊素铭,译.北京:机械工业出版社,2010.

A Simulation Study on the Shift Schedule of ElectricVehicle Aiming at Fuel Economy

Jiang Hao, Zhao Han, Huang Kang & Liu Fuxiao

SchoolofMechanicalandVehicleEngineering,HefeiUniversityofTechnology,Hefei230009

In order to extend the driving mileage and reduce the energy consumption of electric vehicle, its shift schedule is simulated aiming at fuel economy in this paper. Firstly, a static economical shift schedule with two-parameter control is worked out. Then by using dynamic programming algorithm, the optimal gear under ECE driving cycles is found, and based on which the static economical shift schedule is revised with the final economical shift schedule curve obtained. Finally an electricity consumption model for electric vehicle is set up, and a simulation on the shift schedule before and after revision is conducted with UDDC driving cycles. The results show that the revised shift schedule can effectively reduce the energy consumption of electric vehicle.

electric vehicle; energy consumption; static economical shift schedule; dynamic programming; electricity consumption model

*国家863计划项目(2011AA11A236)资助。

原稿收到日期为2013年7月2日，修改稿收到日期为2013年9月27日。