利用多代卫星测高数据计算中国近海及邻域重力异常

刘善伟, 李家军, 万剑华, 杨俊钢

(1.中国石油大学(华东) 地球科学与技术学院, 山东 青岛 266580; 2.国家海洋局第一海洋研究所 山东 青岛 266061)

随着卫星测高技术的发展, 积累了大量的卫星测高数据集, 为恢复海洋重力异常提供了丰富的数据资料, 联合利用多颗卫星的测高数据是求解高精度、高分辨率海洋重力异常的主要技术。Sandwell[1]、Andersen等[2]利用ERS-1、Geosat/GM等多颗卫星的测高数据分别解算了全球海洋重力异常; Hwang等[3]采用Seasat、Geosat/GM/ERM、ERS-1和T/P等多颗卫星的数据, 利用 Vening-Meinesz公式和一维 FFT技术得到了 2′×2′分辨率的全球海洋重力异常; 王海瑛等[4]利用T/P、ERS-1和Geosat/GM三颗卫星的测高数据解算 2′×2′中国南海区域重力异常, 精度为10mgal左右; 李建成等[5]采用T/P、ERS-2和Geosat卫星的测高资料, 确定了 2.5′×2.5′中国近海重力异常, 其精度为9.3 mgal。以往研究所用卫星数量一般为3～4颗, 其重力异常计算精度偏低。

本文联合 Jason-1/2、T/P、Envisat、ERS-1/2、Geosat等 7颗卫星的测高资料, 利用逆 Vening-Meinesz 公式计算中国近海及邻域(0°～42°N, 100°～140°E)2′×2′重力异常。

1 研究数据与方法

1.1 研究区域与数据

研究区域为中国近海及周边邻域(0°～42°N,100°～140°E)如图1 所示。采用 Geosat、ERS-1/2、Envisat、T/P、Jason-1/2等卫星的测高数据(表1), 图2是图1方框区域对应的多星测高数据地面轨迹, 通过多星联合有效提高了测高数据的观测密度。本文选用的卫星测高数据精度为3～20 cm, 多星数据联合平差可在一定程度上克服卫星测高数据的系统误差;在利用逆 Vening-Meinesz公式反演海洋重力场时,重力异常反演精度与测高误差成正比[6], 其通过海面高差(非海面高)推估海洋重力场, 能够进一步削弱系统误差的影响, 但不能消除偶然误差, 而不同卫星的偶然误差大小不同, 其对重力异常反演精度有一定影响。

表1 卫星测高数据基本信息表Tab.1 Basic satellite altimeter data

图1 研究区域Fig.1 Study area

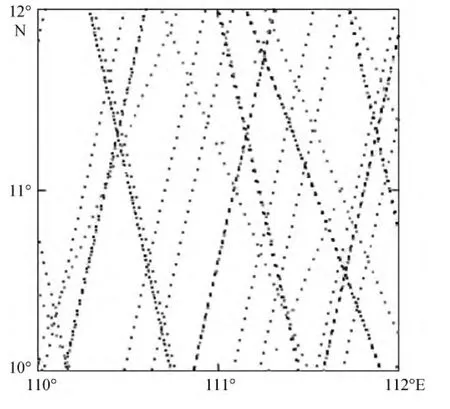
图2 多星测高数据地面轨迹Fig.2 Multi-satellite altimetry data track

1.2 逆Vening-Meinesz公式计算重力异常

逆 Vening-Meinesz公式由垂线偏差计算转换到重力异常公式[3]如公式(1)所示。

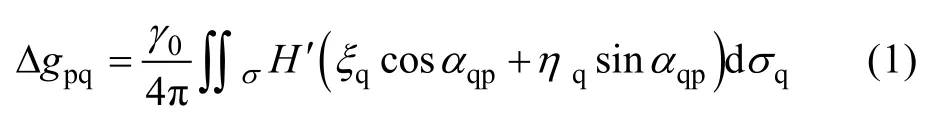
式中,0γ为平均重力, p为计算点, q为流动点,αqp为q点到p点的方位角,qξ和ηq分别为q点垂线偏差的子午分量和卯酉分量,H′为积分核函数的导数。

γ0的计算公式为

式中,GM为地球引力常数, 本研究以T/P卫星参考椭球为基准,GM取值为398 600.441 5 km3/s2,R为地球平均半径。

逆 Vening-Meinesz公式的关键是确定一个将垂线偏差转换为重力异常的合适的核函数, Hwang给出的核函数表达式为

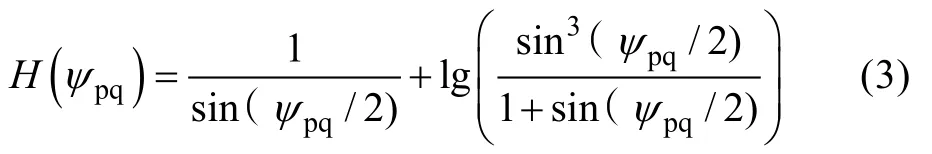
ψpq为p点到q点的球面距离。

2 数据预处理

2.1 ERM数据共线处理

测高卫星ERM任务设计为精确重复轨道, 但实际同一测高卫星在不同周期内的地面轨迹会产生偏移, 该偏移最大不超过1 km。卫星测高数据共线处理, 将并非严格重复的轨迹归化到同一参考轨迹上,不仅可以压缩数据量, 还可以抑制和减小时变因素的影响, 降低随机噪声, 减弱动态海面地形的影响,提高测高数据的精度[7]。借鉴 Geosat/ERM 数据的共线处理方法[8]对各卫星 ERM 数据进行共线处理,并统计共线处理前后研究海域内交叉点处不符值的均方根(表2), 可看出交叉点不符值显著减小, 经过共线处理后的海面高度显著削弱了海面时变的影响。

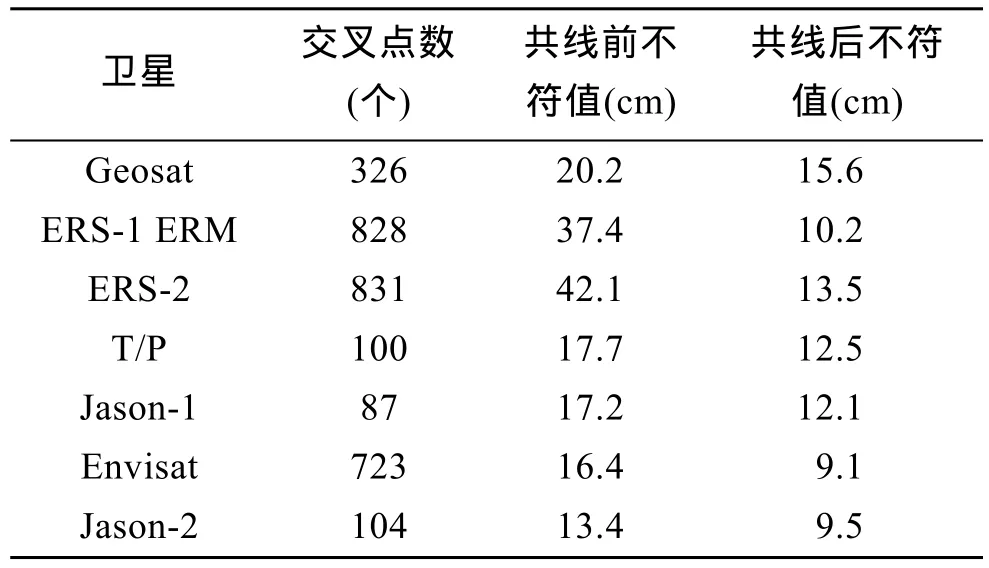
表2 共线处理前后交叉点不符值均方根统计Tab.2 Statistical cross points difference RMS before and after collinear processing

2.2 多星联合平差

通过自交叉点平差处理Jason-1/2、T/P、Envisat、ERS-1/2、Geosat等卫星的测高数据, 消除不同年代其内部及相互之间的不协调性。在此基础上, 以T/P卫星所采用的地球参考坐标框架和地球椭球为基准,将其它种类的卫星测高数据统一到同一基准, 即固定所有的T/P测高弧段, 逐一进行其它卫星与T/P卫星之间的互交叉点平差处理。平差方法采用验后条件平差法[9-10], 各卫星数据自交叉点平差前后的的海面高不符值统计如表3所示, T/P卫星与其他卫星互交叉点平差前后的海面高不符值的统计结果如表4所示。

表3 自交叉点平差前后交叉点不符值均方根统计Tab.3 Statistical cross points difference RMS before and after crossover adjustment

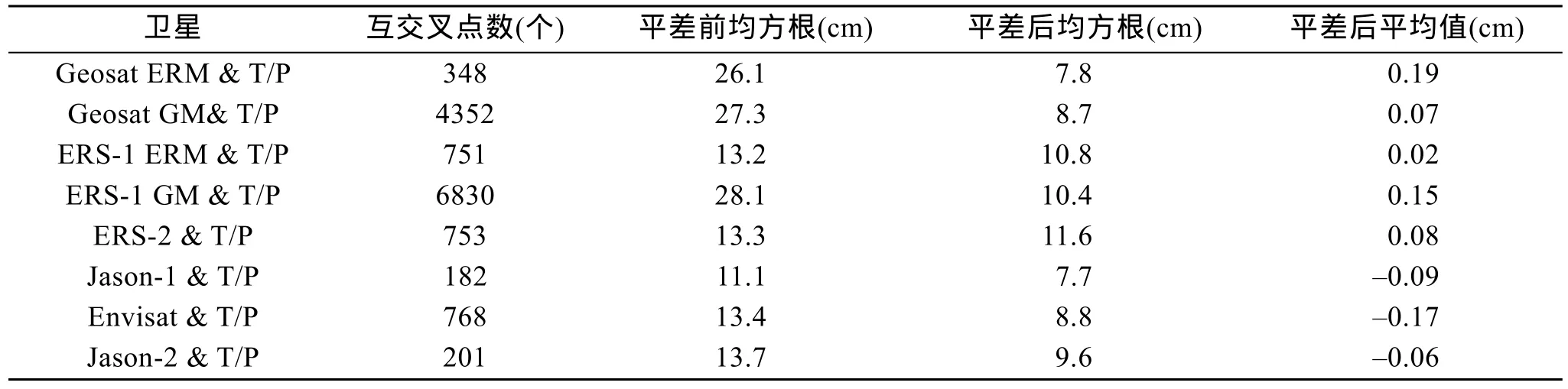
表4 多星交叉点平差前后交叉点不符值统计Tab.4 Statistical cross points difference RMS before and after crossover adjustment

表3和表4说明, 多星数据联合平差处理效果理想。经过交叉点平差, 海面高交叉点不符值均方根由平差前9～27 cm下降到平差后的5～11 cm, 效果显著,基本消除了各卫星测高数据自身内部的不协调性;T/P卫星与其它卫星数据之间存在系统误差, 且大小不一, 主要由于它们采用了不同的参考椭球、参考框架和改正模型, 通过互交叉点平差消除了多星之间的不协调性, 海面高交叉点不符值的均方根由平差前的11～28 cm下降到平差后的7～11 cm, 实现了多代卫星测高数据基准的统一。

3 结果与讨论

3.1 重力异常计算

基于参考模型 DOT2008A海面地形模型和EGM2008重力场模型, 采用移去-恢复技术, 首先根据 Hwang[3,11]的方法计算测高点剩余沿轨垂线偏差,利用最小二乘原理, 计算网格残余垂线偏差分量。选择残余垂线偏差范围为 0～3″, 积分半径为 30′[12], 将网格残余垂线偏差分量带入逆 Vening-Meinesz公式计算中国近海及邻域 2′×2′分辨率的残余重力异常,然后借助 EGM2008重力场模型恢复 2′×2′的重力异常, 计算结果如图3和图4所示。

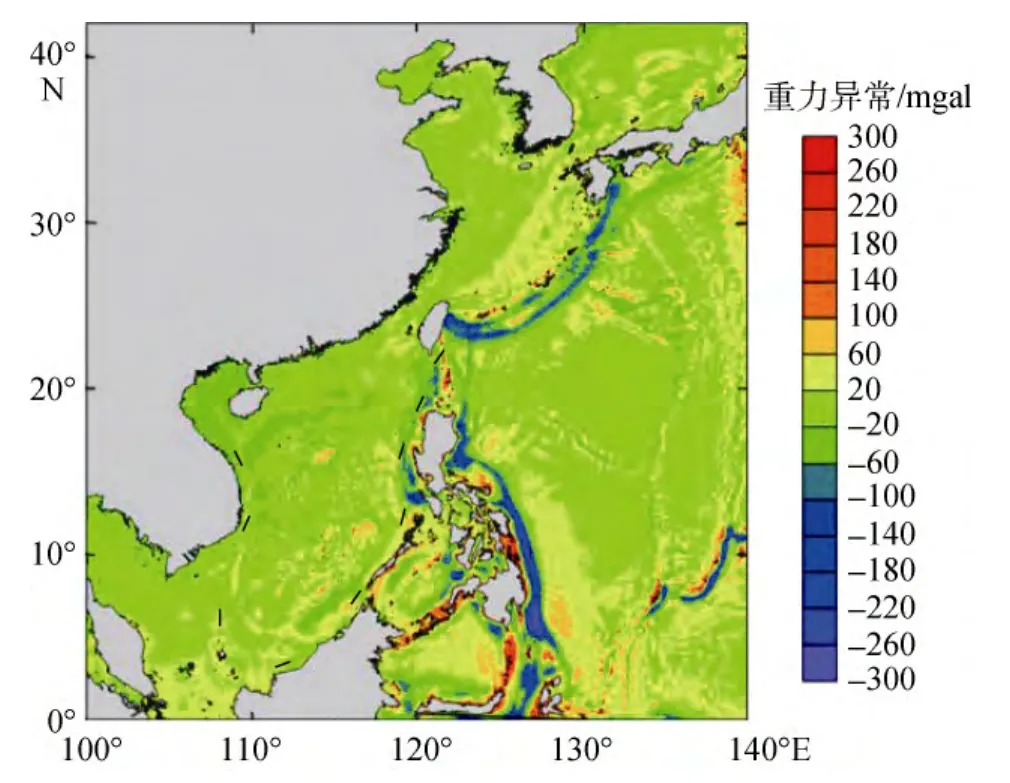
图3 重力异常Fig.3 Gravity anomalies

图4 局部重力异常等值线图(mgal)Fig.4 Local map of gravity anomaly contours

3.2 结果讨论

为检验重力异常计算结果的可靠性, 采用船测重力数据(由美国国家海洋与大气机构 NOAA提供,http: //www.ngdc.noaa.gov/mgg/gdas/ims/trk_cri.html)检验重力异常计算结果的精度, 分布范围见图5,红色点代表船测重力异常点, 共17 536个。以卫星测高数据计算的 2′×2′重力异常网格数据为基础数据, 内插出船测数据点重力异常, 针对反演重力异常和船测数据制作散点图(图6)和重力异常差值直方图(图7), 并在此基础上进行误差统计(表5)。

图5 船测重力数据点Fig.5 Shipboard gravity data points

由图6看出, 反演重力异常和船测数据相近, 围绕y=x直线分布, 表明两者数值相符, 但同时存在误差较大的点; 由图7看出, 差值基本围绕x=0对称分布, 且差值多分布于-10～10 mgal之间, 有较强的集中性; 由表5看出, 卫星测高反演重力异常与船测观测值之间存在负的系统性偏差, 可能与参考场误差、坐标及重力系统转换误差有关。本文利用卫星测高数据反演海洋重力异常值精度为5.4 mgal, 计算精度与文献[13]提及的理论估算水平(5.4 mgal)一致, 略高于前人成果[4,5,13-14]。原因有以下几点: (1)较以往研究, 选择的卫星数量多且精度高, 引入了Jason-1/2、TP高精度测高数据, 并且除Geosat外, 测高精度都在10 cm以内; (2)卫星测高数据集时间跨度大(1985年3月～2013年7月), 有助于削弱短波信号误差; (3)以最高精度的T/P卫星测高数据为基准开展了多星数据的联合平差处理, 削弱了不同卫星测高数据之间的不协调性。

表5 反演重力异常与船测数据的总体比较Tab.5 Total comparison of study results and that of shipborne data

图6 重力异常比较散点图Fig.6 Gravity anomaly comparison scatter

图7 重力异常差值直方图Fig.7 Gravity anomaly difference histogram

4 结语

基于 Jason-1/2、T/P、Envisat、ERS-1/2、Geosat等卫星测高数据, 利用逆 Vening-Meinesz公式计算中国近海及邻域(0°～42°N, 100°～140°E)2′×2′重力异常, 精度为5.4 mgal, 表明Jason-1/2、T/P等高精度卫星测高数据的引入可提高海洋重力场计算精度。

多项平差处理是提高海洋重力场计算精度的重要手段。ERM数据共线处理能够明显减弱测高数据自身时变因素影响, 而多星数据联合平差处理则能够削弱测高数据内部和相互之间的数据不协调性,有效降低交叉点不符值的均方根。

[1] Sandwell D T.Antarctic marine gravity filed from high-density satellite altimetry[J].Geophys J Int, 1992,109: 437-448.

[2] Andersen O B, Knudsen P.Global marine gravity field from the ERS-1 and Geosat geodetic mission altimetry[J].Geophys J Res, 1998, 103(C4): 8129-8137.

[3] Hwang C, Eu C K, Barry P.Global derivation of marine gravity anomalies from Seasat, Geosat, ERS-1 and TOPEX/POSEIDON altimeter data[J].Geophys J Int,1998, 134: 449-459.

[4] 王海瑛, 王广运.卫星测高数据的沿轨迹重力异常反演法及其应用[J].测绘学报, 2001, 30(1): 21-26.

[5] 李建成, 宁津生, 陈俊勇, 等.联合 TOPEX/Poseidon,ERS2和Geosat卫星测高资料确定中国近海重力异常[J].测绘学报, 2001, 30(3): 197-202.

[6] 彭富清, 陈双军, 金群峰.卫星测高误差对海洋重力场反演的影响[J].测绘学报, 2014, 43(4): 337-340.

[7] Yale M M, Sandwell D T, Smith W H F.Comparison of along-track resolution of stacked Geosat, ERS 1, and TOPEX satellite altimeters[J].Journal of Geophysical Research: Solid Earth (1978-2012), 1995, 100(B8): 15117-15127.

[8] 褚坤.Geosat高度计数据处理与南海重力异常反演精度评价[D].青岛: 中国石油大学(华东), 2010.

[9] 刘传勇, 暴景阳, 黄谟涛, 等.验后平差方法在Geosat/ERM 卫星测高数据处理中的应用[J].海洋测绘, 2008, 28(1): 5-8.

[10] 黄谟涛, 王瑞, 翟国君, 等.多代卫星测高数据联合平差及重力场反演[J].武汉大学学报, 2007, 32(11): 988-993.

[11] Hwang C, Hsu H Y, Jang R J.Global mean sea surface and marine gravity anomaly from multi-satellite altimetry: applications of deflection-geoid and inverse Vening Meinesz formulae[J].Journal of Geodesy, 2002,76(8): 407-418.

[12] 李娜, 章传银.用逆 Vening-Meinesz 公式反演海洋重力场时积分半径的选择[J].大地测量与地球动力学, 2009, 29(6): 126-129.

[13] 黄谟涛, 翟国君, 欧阳永忠, 等.利用多代卫星测高数据反演海洋重力场[J].测绘科学, 2006, 31(6): 37-39.

[14] 黄谟涛, 王瑞, 翟国君, 等.多代卫星测高数据联合平差及重力场反演[J].武汉大学学报: 信息科学版,2007, 32(11): 988-993.