巧用“数形结合”，培养学生几何直观能力

江苏常州武进清英外国语学校（213164） 沈 静

几何直观能力主要指利用图形描述或分析问题的能力。在小学数学学习的过程中，有许多学习内容既具有“数的特征”，又具有“形的特征”，采取“数形结合”的方法不仅可以使复杂的数学问题简单化、明朗化；还可以将图形问题转化为代数问题，帮助学生获得准确的数学结论，形成数学直观能力。具体来说，可以从以下三个方面入手。

一、在计算教学中实现数形结合，培养几何直观能力

在计算教学中，有些教师往往只重视让学生机械重复地训练，这样教学，不仅无法激起学生的学习兴趣，而且枯燥乏味，教学效率低下。在这种教学情形下，教师不妨把计算教学与直观图形结合起来，启发学生思考，活化计算教学，进而使学生的几何直观能力得到有效培养。

这时，教师再引领学生就图形进行观察与思考，让学生想想从图中自己看懂了什么？通过观察，学生很快发现，“这几个分数的和与单位“1”刚好差了1个因而就得出了

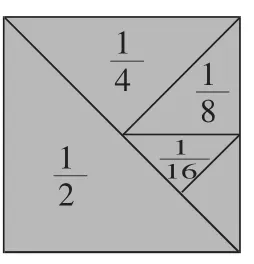
由此可见，在计算教学中，巧用数形结合，不仅使学生的计算效果得到了保证，而且还有效促进了学生几何直观能力的形成。

二、在概念教学中实现数形结合，培养几何直观能力

在概念教学时，教师如果只是让学生死记硬背概念，而学生对概念的由来一无所知，那么，这种教学方式将不利于学生应用能力的提升。因此，在概念教学时，教师不妨引导学生把概念教学与数形结合起来，使学习内容显得形象直观，同时有效培养学生的几何直观能力。

如在教学“求一个数的几倍是多少”时，学生最难理解的是，“倍”指的是什么？几倍又指的是什么？怎样才能使学生对“倍”这个概念有直观形象的认识，并且把“倍”这个概念内化为学生自己的知识呢？以“小明叠了4个五角星，小华叠的是小明的3倍，求小华叠了多少个。”为例，在教学时，笔者是这样帮助学生建构概念的：首先，让学生根据习题要求并用上数学符号把小明和小华叠的数量分别画下来，结果如下：

小明：★★★★（4个）

小华：★★★★ ★★★★ ★★★★（？个）

然后，让学生进行观察与思考，并说说这两幅图之间有什么区别，从而使学生可以直观形象地认识到如果以小明叠的数量1份为标准，看做1倍的话，那么，小华叠的里面有几个这样的一份，就是几倍。由个数引出份数，再到倍数，这样教学，学生会倍感轻松。

由此可见，在数学概念的教学中，教师要能够根据习题的性质，引出恰当的图形，通过数形结合，使抽象的数学概念直观化，从而帮助学生形成概念。

三、在解决问题中实现数形结合，培养几何直观能力

在数学解决问题的教学中，为了培养学生的几何直观能力，教师可以引导学生采取数形结合的方法来解决。

如在解决“明明和佳佳一共有520元钱，明明花去了自己总钱数的2/5，佳佳花了40元，结果他们两人剩下的钱数一样多，你知道明明和佳佳原来各有多少钱吗？”这个数学问题时，学生一致认为画图解决比较简便，在教师的启发下，学生画图如下：

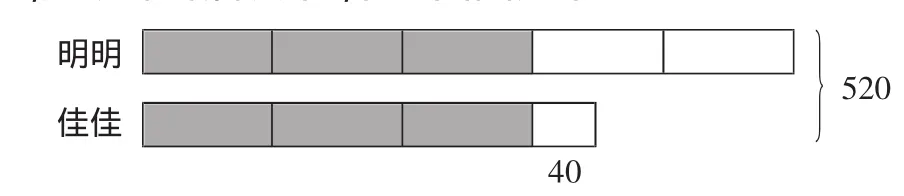
根据图示，学生很快答出了8个单位＝520-40＝480（元），480÷8＝60（元）；明明原有钱＝60×5＝300（元）；佳佳原有钱＝60×3＋40＝220（元）。在这样直观形象的图示中，学生解决起问题来既简便又轻松，提高了学习效果。

由此可见，借助数形结合不仅可以帮助学生理清解题思路，降低学习难度，与此同时，学生的几何直观能力也得到了极大培养，提升了学习效果。

总之，要想使学生的几何直观能力得到有效培养，教师唯有把“数形结合”巧妙地运用到数学教学的各项内容之间，才可以在降低学生学习难度的同时，使学生的几何直观能力得到有效培养。