培养中年级学生画图解题能力探微
江苏连云港市灌云县侍庄中心小学(222200) 孙宝霞
数学课程标准指出要让学生在学习过程中,获得分析问题和解决问题的一些基本方法,形成初步的反思意识,这就要求学生有一定的解题能力。在小学阶段,中年级学生的思维正处于由具体形象思维向抽象逻辑思维过渡的阶段,学生的抽象思维过程仍然需要具体形象的支持。况且,形象化的实例容易引起学生的兴趣,激发学生学习的积极性,提高学生分析问题和解决问题的能力。
作为一线数学教师,笔者发现学生在解决没有图示的实际问题时会出现很多的错误,除不能很好地审清题目、理解题意之外;更主要的是学生借助画图策略解决数学问题的意识不强,绘图能力不足,从而导致解决数学问题不力。为此,在平时教学过程中,笔者在画图解题方面做了很多的探索和尝试,从而切实提高学生的解题能力。
一、画图教学,模型搭建直观形象
教育大师苏霍姆林斯基说过:“孩子的智慧在手指上。”数学题的内涵经过学生灵巧又智慧小手绘制出来,无论是“力作”还是“劣作”,我们都要一视同仁地肯定其存在价值,都要尽可能地让学生说出作品的意思以及自己的思想。在教学过程中,笔者和学生经常会通过一些线段图、集合图等来帮助理清题目中的已知条件和所求问题,使问题简明直观;其间可以展示其数学思维过程,窥视其数学建模情况,闪烁其数学思维火花。
1.多样线段图
线段图简洁明了,形象易学。笔者在教学和倍、差倍问题时,根据题意作出线段图,从图中学生可以很快地理解和、差与一份数之间的关系,从而提升分析问题的能力。
例如:两个小朋友去森林里采蘑菇,小红采的个数比小丽的3倍还多5个,他们一共采了53个,两人各采了多少个?
这个是变式后的和倍问题,学生通常很难一下子理解这个5到底该怎么处理,笔者就建议先画图看一看。

通过画图,学生可以发现,53减去5之后正好就是小丽所采蘑菇的3倍,可以马上求出小丽所采的蘑菇个数,接着就可以求小红所采的个数了。简单的线段图可以让学生更直接地分析每个量之间的关系,使题意更直白、外显,便于理解,提高解题速度和解题质量。
另外,用画线段图来理解较复杂的行程问题也是再清楚不过的了。
例如:一辆货从A地开向B地,每小时行45千米,行了3小时后休息,这时刚好离AB两地的中点18千米,东西两城相距多少千米?
通过画图发现,有两幅图都符合题意:
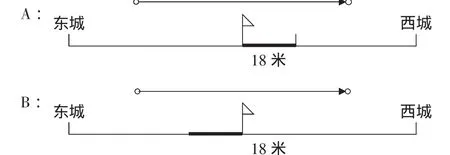
线段图除了可以帮助我们整理题目中的条件和问题,还可以帮助我们更全面地理解题意。根据这两幅图我们就可以得到两种不同的答案:
45×3=135(千米) 135+18=156(千米) 156×2=312(千米)
45×3=135(千米) 135-18=117(千米) 117×2=234(千米)
在不画图的情况下,多数学生都不会想到这一题会有两种不同的答案,但就在画线段图的过程中,学生能更好地去理解题意,去考虑离中点18米的位置到底在哪。可见,画图可以让学生更全面深入地思考,还可以让学生在解题后更快更直观地对结果的正确性进行检验。
2.巧画集合图
例如:某班有学生42人,全班每人至少要订一种报纸,订数学报的有24人,订语文报的有28人,问两种报都订的有多少人?
读题后,学生自行画图(如右图所示)。
引起争议:24+28=52 人,与题目中的42人矛盾。
引导学生思考:为什么?该如何解决?
学生讨论再作修改(如右图所示)。
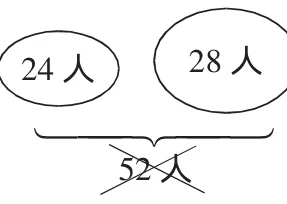
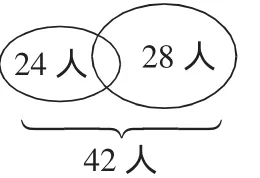
提问:为什么这样修改?两个圆相交的部分是什么?
从题目中学生可以确定订两种报的人数之和应为24+28=52(人),可是全班总人数只有 42 人,相差 52-42=10(人),说明有10人两种报纸都订了。
在绘画和理解集合图的同时,学生也就找到了解题的钥匙。运用画图策略,让冰冷的数学文字变为一幅幅图,再配以形象生动的语言描述,让数学关系自然呈现。整个过程生动活泼,学生学得轻松且高效。
二、画图教学,数形结合完美演绎
我国著名数学家华罗庚对“数”与“形”之间的密切联系有过一段精彩的描述:“数与形本是相依,焉能分作两边飞,数缺形少直觉,形少数难入微,数形结合百般好,隔裂分家万事休,切莫忘,几何代数统一体,永远联系切莫分离。”在教学过程中,笔者尝试数形结合的教学受到了学生的欢迎,也取得较好的教学效果。
1.利用列表法解题
例如:新华小学准备建一个周长是20米的长方形花圃,你能设计出多少种不同的情况?
碰到这样的问题,学生确定了长、宽的关系后也很难一下子就把所有的情况全都表达清楚,所以建议学生用列表格的方法解决。表格为:

长(米) 9 8 7 6 5宽(米) 1 2 3 4 5
明确长和宽的关系后,把每一种可能进行列表整理,学生就可以非常清楚地看出有5种不同的情况,既直观又明了。
另外,对于一些数据较多的问题,学生在理解时,往往会对不上号,如果用了列表的方法,就更容易理清题意,也易于揭示数量之间的关系,便于理顺思路,进行解答。
2.利用面积图解题
数形结合是教学几何初步知识与培养空间观念的重要方法,在某些几何题中可采用面积图来解题。
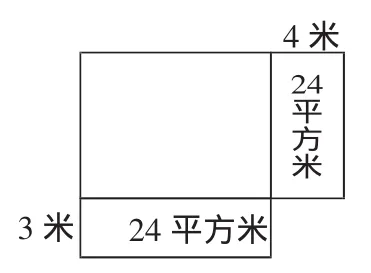
例如:一个长方形长增加4米,或宽增加3米,面积都增加24平方米,求原长方形的面积。
根据题意可画出右图:
根据图形学生进行分析:要求原来的面积,需要知道长和宽,但是,现在什么都不知道。在这样的情况下,学生会根据需要继续从图形出发,从变化的图中找到求原来的长与宽的方法,结果,学生就得到了这样的计算过程:
长:24÷3=8((米)
宽:24÷4=6(米)
所以原长方形的面积为:8×6=48(平方米)
运用面积图不仅可以快速找到解题途径,还能找到更巧妙的解题方法。
如在教学“用画图法解决面积计算”这一课之后,笔者给学生出了这样一题:
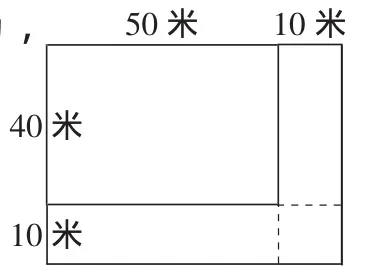
张庄小学原有一个长方形操场,长50米,宽40米,扩建校园时,长和宽都增加了10米,求:新增的面积是多少平方米?
某学生一口气就找到了四种不同的解法。
方法一:(50+10)×(40+10)-50×40
方法二:40×10+(50+10)×10
方法三:40×10+50×10+10×10
方法四:(40+10)×10+50×10
运用面积图解题,实质就是化抽象为形象。中年级学生的抽象能力原本就不强,加上很多学生对解决问题有一种本能的恐惧,所以更不愿意去深入思考题意。但如果能让学生边读题边画出相应的图形,并标上数据,在形象的几何图上来理解题意当然要比让他们在脑子中想象现实得多,也容易理解得多。所以利用几何直观图不仅可以帮助学生理清解题思路,也能帮助他们提高解题能力。
三、画图教学,数学思维深入脑海
解题能力不仅是指解题时有办法、有能力解题,而且是指解题后能够很好地掌握同类题型的解法。而这一目标的达成,一般要通过回顾整个解题过程来实现。
在教学“用画图法解决行程问题”时,笔者就是让学生通过回忆整个解题的过程,最后达到作图方法的优化,把简单的行程问题的解法通过纸上图到心里图的升华深入脑海。
笔者在讲授“鸡兔同笼”问题时,教给了学生如何画替换图的方法。如有这样一题题:鸡兔同笼,头共20个,足共62只,求鸡与兔各有多少只?
学生先用假设法,假设全鸡,20只鸡,有40条腿。

分析:少了62-40=22(条)腿。因为兔子有 4 条腿,才画了2条腿,每只兔子需要再加2条腿。

因此,兔子有 22÷2=11(只),鸡有 20-11=9(只)。
生动、形象的图例,激发了学生学习的兴趣,从简单中看到深奥,学生很快找到了解题方法。
数形结合是一种非常重要的数学思想方法,通过画图,学生能仔细地审题、分析数量关系,做完后,与图形的又一次对比,更能让他们从中收获巧妙的解题方法。
因此,从中年级开始我们就要注重培养学生运用作图的方法来解决实际问题。以画图为拐棍,让学生尝到学习数学的无穷乐趣和成功体验,从而真正提高他们的解题能力;让画图成为学生学习数学过程中简单实用而又快捷方便的一把“金钥匙”。

