电压型级联系统中减小源变换器输出阻抗的有源阻尼控制方法

贾鹏宇 李 艳 郑琼林

电压型级联系统中减小源变换器输出阻抗的有源阻尼控制方法

贾鹏宇 李 艳 郑琼林

（北京交通大学电气工程学院 北京 100044）

在级联系统中，源变换器和负载变换器之间阻抗的相互作用可能会影响系统的稳定性。许多文献分析了不同控制方法、电路参数等因素对变换器阻抗特性的影响，并针对优化变换器的阻抗设计提出了多种无源阻尼或者控制的方法，从而提高变换器的稳定裕度，以保证变换器构成的级联系统维持稳定。本文基于变换器的小信号模型，提出了一种实现虚拟电阻的有源阻尼控制方法，以降低变换器的输出阻抗，优化其阻尼特性。该方法通过采样变换器输出电压中的交流分量，经过有源阻尼控制器作用后叠加至调制波以产生控制信号，从而实现在变换器小信号模型的输出端连接虚拟电阻的效果，达到降低输出阻抗的目的。由于虚拟电阻仅存在于小信号模型中，所以变换器的稳态工作点不受影响。通过仿真和实验验证了该方法的正确性。

级联系统 DC-DC变换器 输出阻抗 虚拟电阻 有源阻尼 稳定性

1 引言

在分布式电源系统中（Distributed Power System, DPS），存在多种源变换器和负载变换器级联的情况。源变换器的输出阻抗 Zout和负载变换器的输入阻抗 Zin是与变换器级联系统稳定性相关的重要参数。当系统中变换器分别独立稳定时，级联后系统的稳定性取决于阻抗比Zout/Zin是否满足奈奎斯特稳定判据[1]。

为了保证变换器级联后构成的电源系统依然稳定并且具有一定的稳定裕度。许多文献针对变换器的阻抗设计提出了禁止区域的概念作为设计准则[1-5]，即要求阻抗比 Zout/Zin构成的奈奎斯特曲线不得进入坐标中设定的区域，从而保证级联系统具有一定的稳定裕度。

由于禁止区域仅约束了阻抗比曲线在极坐标系中的位置从而保证级联系统的稳定性，而没有给出具体优化变换器阻抗特性的方法，因此其概念较为抽象。为此，许多文献针对降低变换器输出阻抗，优化变换器输入阻抗，改善变换器阻尼特性进行了大量研究，并提出了多种具体的实现方法。文献[6-9]对影响变换器阻抗的因素进行了归纳分析，研究了不同电路参数、控制方法对变换器阻抗的作用，并给出了优化变换器阻抗的控制器设计方法。带有LC滤波器的恒压变换器可以看成是最简单的级联系统。由于恒压变换器的输入阻抗在低频处表现为负阻特性，常常与 LC滤波器的输出阻抗相互作用导致系统发生振荡，因此文献[10]给出了采用不同的阻尼回路改善 LC滤波器阻尼特性的方法，从而减小滤波器的输出阻抗，提高级联系统的稳定性。针对上述系统，文献[11]对滤波器电容并联 RC阻尼回路的方法进行了深入分析，给出了 RC阻尼回路参数的设计过程。文献[12]探讨了 RC阻尼回路扩展应用于源变换器和负载变换器构成级联系统的情况，分析了将 RC阻尼回路并联至源变换器输出端口的情况，给出了阻尼参数的设计方法，以降低源变换器的输出阻抗，保证系统稳定。

增加阻尼回路的方法会产生附加损耗，降低变换器的效率。因此，一些文献针对采用不同的控制方法提高级联系统的稳定性进行了研究。文献[13]提出了一种输出电流前馈的控制方法，以实现变换器输出阻抗近似为零，从而达到前后级变换器阻抗解耦的目的。文献[14-19]提出了多种有源阻尼的控制方法，但需要针对特定的滤波器结构进行设计。其中，文献[14-17]提出了针对 AC-DC变换器中LC/LCL滤波器进行有源阻尼的控制方法；文献[18]提出了一种适用于含有 LCL输出滤波器的 DC-DC变换器的有源阻尼方法；文献[19]针对基本变换器拓扑，提出了一种在电感支路中模拟出等效串联电阻的有源阻尼方法。

另外，文献[20-22]提出了向级联系统中引入解耦变换器的方法，减小前后级变换器阻抗的相互作用，实现系统稳定。但是引入的解耦变换器增加了系统的成本和体积。

针对 DC-DC变换器，本文提出了一种有源阻尼控制方法，可以实现变换器小信号模型的输出端等效模拟出并联虚拟电阻的效果，从而降低输出阻抗，改善其阻尼特性。当采用有源阻尼控制的变换器作为级联系统中的源变换器时，通过调整其虚拟电阻值，可以降低源变换器的输出阻抗，减小其输出阻抗与后级负载变换器输入阻抗的交截范围，从而改善级联系统的稳定性。

2 DC-DC变换器的通用小信号模型

DC-DC变换器的工作点决定了此时变换器的大信号模型和小信号模型。大信号模型取决于变换器稳态工作点处的直流电压增益比，而小信号模型取决于稳态工作点处的交流小信号扰动构成的输入输出关系[23]。图1所示为一般 DC-DC变换器处于某一稳态工作点时，考虑外加电源内阻效应和负载效应时的小信号模型，点划线框内表示变换器本身的模型，包括输入电压、输入电流、控制信号、输出电压和输出电流共 5个变量。其中，Yin表示开环输入导纳，Toi表示输出电流-输入电流传递函数，Gci表示控制量-输入电流传递函数，Gvg表示开环输入电压-输出电压传递函数，Gco表示控制量-输出电压传递函数，Zout表示开环输出阻抗。在图1中，电源内阻用 Zs表示，负载阻抗用 ZL表示。因此，不考虑电源效应和负载效应时，虚线框内变换器本身的小信号模型可用矩阵方程式（1）来表示，也称为G参数矩阵[24]。作为状态方程的输出矩阵，以及作为状态方程的输入矩阵。

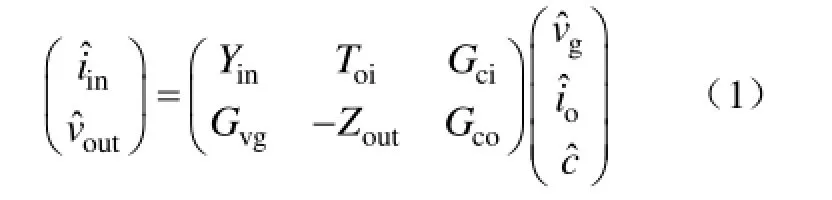
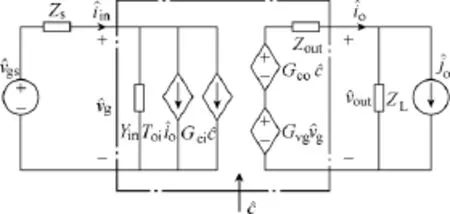
图1 考虑电源阻抗效应（, Zs）和负载效应（, ZL）的变换器小信号模型Fig.1 Small signal model of a converter with nonideal source（, Zs）and load（, ZL）

当考虑负载效应的影响时，根据图1可知，式（2）、式（3）成立，即

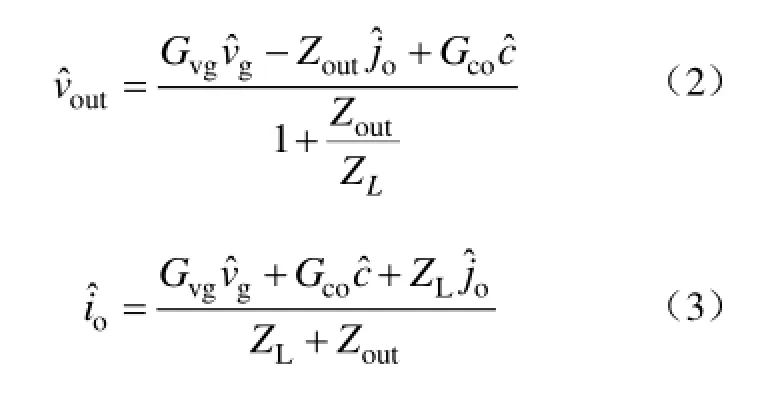
将式（2）、式（3）代入矩阵方程式（1），可以得到矩阵方程式（4）。式（4）描述了考虑负载效应 ZL时，变换器小信号模型的 G参数矩阵受负载影响发生的改变。其中，电流扰动代替作为输入矩阵的变量，即

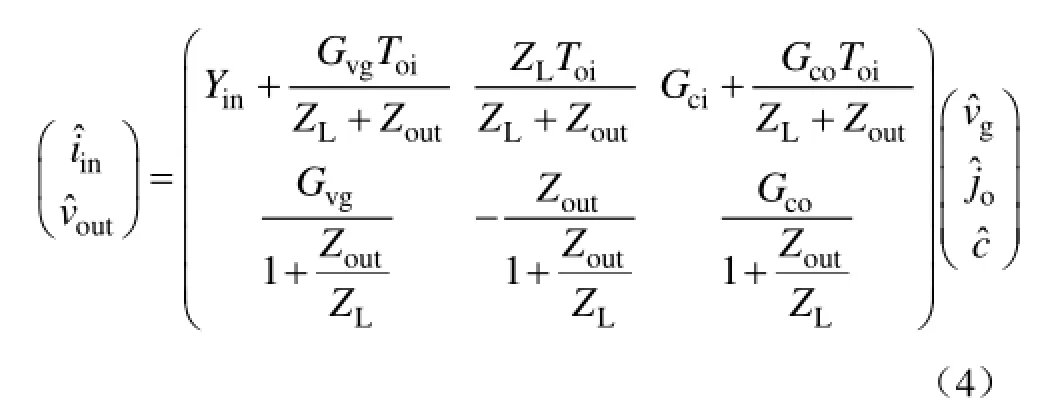
根据上式可知，当考虑负载效应对小信号模型的影响时，变换器的控制量-输出电压传递函数和输出阻抗可以分别表示为

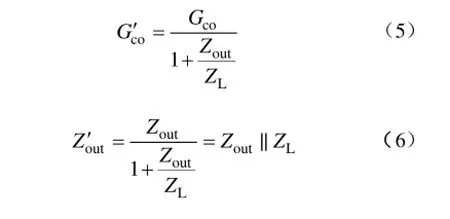
其中，Gco与Zout分别表示无负载效应时的参数。

需要强调的是，在考虑负载效应 ZL对小信号模型的影响时，图 1点划线框内表示的变换器本身的小信号模型未发生改变。这就意味着考虑负载效应前后的变换器小信号模型应处于同一稳态工作点。

3 DC-DC变换器的有源阻尼控制

考察级联系统中源变换器的输出阻抗时，为了避免后级负载效应的影响，变换器的负载应采用恒定电流负载进行计算和分析[24]。图 2所示为同一个DC-DC变换器分别连接恒定电流负载和恒定电阻负载的两种情况，这里定义恒流负载变换器和恒阻负载变换器进行区分。其中大写字母表示稳态值，小写字母表示扰动量。d表示占空比，Gvd和 Zout分别表示输出端连接恒流负载时变换器的小信号模型参数，其中Gvd表示占空比-输出电压传递函数，Zout表示输出阻抗。当变换器连接恒阻负载R时，用

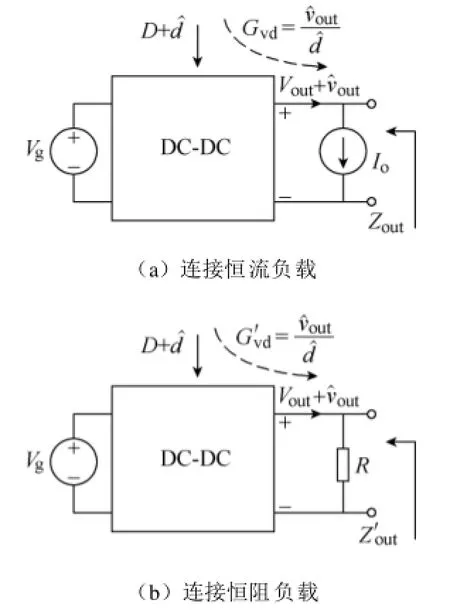
图2 连接不同负载时DC-DC变换器结构框图Fig.2 Block diagram of DC-DC converter with different loads

在小信号模型中，恒流负载Io不存在负载效应，而恒阻负载R会引入负载效应。当两变换器处于同一稳定工作点时，根据式（6）可知，图2中Zout与具有以下关系

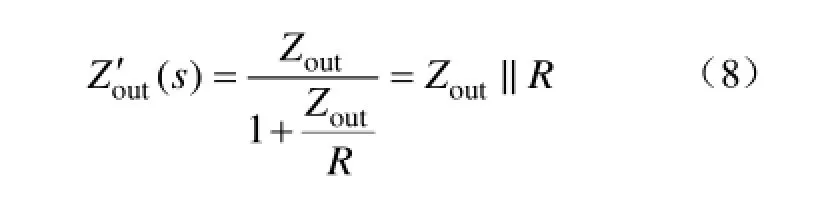
由式（8）可知，对于图2中变换器稳态工作点相同的两种情况，在小信号模型中，由于电阻R提供了阻尼，因此输出阻抗。另一方面，由于变换器输出阻抗与其输出滤波器结构相关，因此电阻R改善了输出滤波器的品质因数[23]。

同样，根据式（5）可知，对于图2所示的两种情况，式（9）成立。

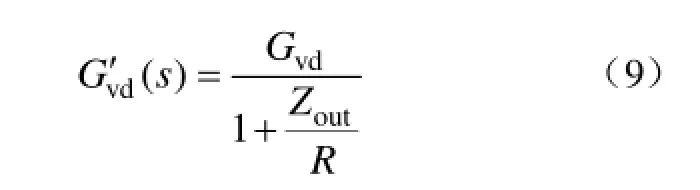
式（8）、式（9）给出了变换器在同一稳态工作点连接不同负载时的对应参数关系。考虑控制信号vcon和调制系数 Fm，根据式（9），可以画出恒阻负载变换器的小信号模型等效框图如图3所示。其中，点划线框整体表示恒阻负载变换器模型，采用恒流负载变换器模型 Gvd和 Zout表示。

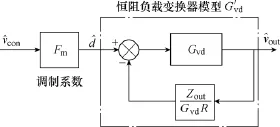
图3 恒阻负载变换器的小信号模型框图Fig.3 Block diagram of the transfer function from control signalto output voltageof the resistor-load converter

对图3进行等效变换，可以得到如图4所示的等效框图。由图 4可知，在小信号模型中，如果对恒流负载变换器的输出电压进行采样，经过特定的反馈采样控制器叠加至控制信号，则可以实现在恒流负载变换器模型的输出端模拟并联负载电阻 R的效果。因此，这里将反馈采样控制器定义为有源阻尼控制器H(s)，其表达式为

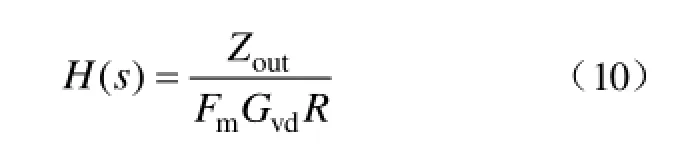
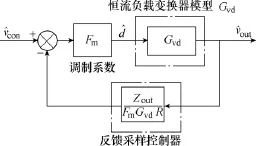
图4 恒阻负载变换器小信号模型的等效变换框图Fig.4 Equivalent transformation block diagram for the small signal model of resistor-load converter

加入有源阻尼控制器之后，恒流负载变换器的控制量-输出电压传递函数以及输出阻抗将等价于恒阻负载变换器的情况。上述讨论基于小信号模型的范围，由于小信号模型中的不同变量分别表示在稳定工作点附近的交流小信号扰动，因此只需采集变换器输出电压的交流分量，进行有源阻尼控制，即可实现模型中的虚拟电阻，降低变换器输出阻抗，不会影响稳态工作点。

根据文献[25]可知，对于同一变换器模型，Gvd与 Zout具有相同的分母，这就意味着当变换器的传递函数Gvd含有右半平面（Right Half Plane，RHP）零点时，理论计算得到的有源阻尼控制器含有RHP极点，这种情况下的有源阻尼控制器无法实现。因此，该方法可扩展至变换器传递函数 Gvd中不含有RHP零点的情况，如全桥、正激、Superbuck、Weinberg以及 HE-Boost等变换器[26]。另一方面，当变换器Gvd中含有RHP零点时，可以采用不含有RHP零点的其他控制器近似控制，从而增加变换器低频段的阻尼，减小其低频段输出阻抗，这将在后续工作中进行研究。

图5给出了采用有源阻尼控制的变换器通过闭环控制调节其输出电压时的控制框图。其中，Hv表示电压采样系数，Gv表示电压环控制器，Vref表示控制信号指令。

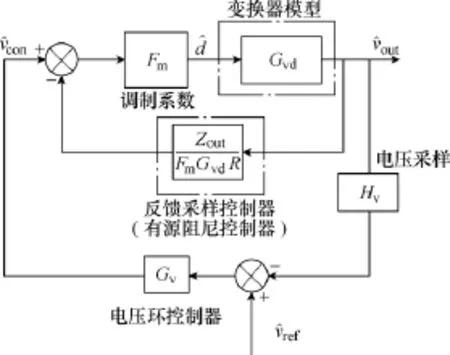
图5 采用有源阻尼控制器的变换器闭环控制框图Fig.5 Control block diagram of a closed-loop converter with the active damping controller

上述讨论了当变换器连接恒流负载 Io，其功率点为 P，输出电压为 Vout时，虚拟电阻等于 R（R=）的情况，即虚拟电阻与稳态功率点相对应。进一步讨论，因为这种方法仅需采样输出电压的交流分量进行有源阻尼控制，因此虚拟电阻仅存在于小信号模型的输出端，所以虚拟电阻值可以任意改变而不影响其稳态工作点。这样可以实现在同一稳定工作点情况下，变换器具有不同的阻尼特性和输出阻抗。换言之，虚拟电阻值无需对应变换器所处的功率点。这种情况一般无法用连接对应阻值的恒阻负载情况进行验证，这是因为当变换器连接的电阻值发生改变时，其稳态工作点也发生了变化，因此小信号模型也会发生改变。

4 Buck变换器的有源阻尼控制器

以恒流负载型 Buck变换器为例，计算其输出端模拟加入虚拟电阻R时的有源阻尼控制器H(s)。图 6所示为 Buck变换器采用有源阻尼控制器的示意图。为了简化计算，仅考虑输出电容的 ESR寄生参数Rc。

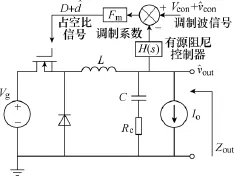
图6 加入有源阻尼控制器的恒流负载Buck变换器控制示意图Fig.6 Control diagram of current-load Buck converter with active damping controller

对于恒流负载 Buck变换器，其输出阻抗和占空比-输出电压传递函数分别表示为

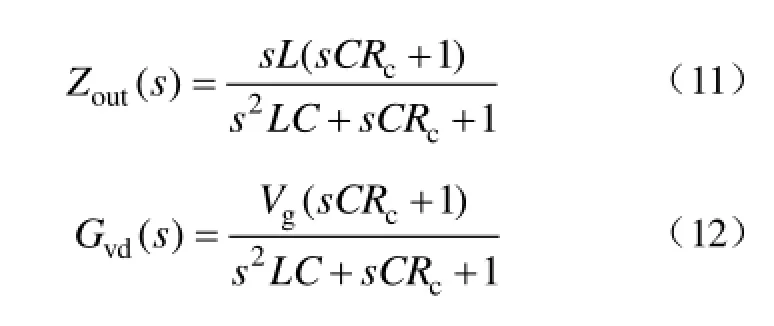
根据式（10）可知，有源阻尼控制器可以表示为

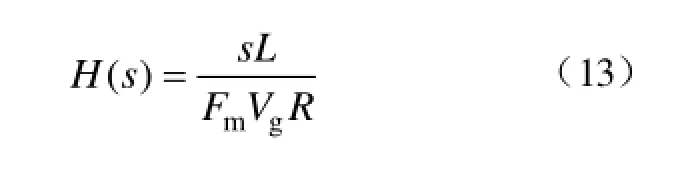
式中，R表示需要进行虚拟的电阻值。当变换器采用幅值为Vm的三角载波进行调制时，调制系数可以表示为

将式（14）代入等式（13）可得

上述分析针对恒流负载型 Buck变换器进行了讨论。当其负载为电阻或者其他变换器时，由式（8）、式（9）可知，负载效应使得变换器传递函数的分母发生了相同的变化。根据式（10）可知，Buck变换器的有源阻尼控制器形式仍然如式（15）所示，即负载效应不会对变换器所需的有源阻尼控制器产生影响。

为了实现在小信号模型中输出端模拟虚拟电阻R，需要对输出电压的交流分量进行采样。由式（15）可知，Buck变换器的有源阻尼控制器形式表现为微分器形式。图 7给出了 Buck变换器中进行有源阻尼控制的实现方法。根据式（15），Buck变换器对应的有源阻尼控制器为微分器，其微分系数为 LVm/ VgR。微分器形式通过图7所示的Ra1、Ca1以及运算放大器实现，因此需要保证 Ra1Ca1=LVm/VgR，即可实现阻值与R相等的虚拟电阻。在实际实验中，为了消除微分器对高频段噪声的微分作用，可以向有源阻尼控制器中加入高频极点电容 Cap以保证变换器的稳定性。由于输出端电压的直流分量经过微分器之后等于零，不会对控制信号产生影响，因此有源阻尼控制器可以直接连接至 Buck变换器的输出侧，而不需要隔离直流分量。

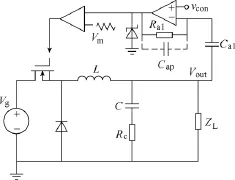
图7 Buck变换器的有源阻尼实现方法Fig.7 The realization of the active damping control in Buck converter

5 仿真与实验验证

5.1 有源阻尼控制器的仿真验证

针对企业的会计财务管理人员操作不熟练、技术水平不高的现状，要加强对财务部门工作人员的培训，一方面要提高他们对ERP系统的认识，改变传统的工作方式；另一方面要提高他们的具体业务操作能力，只有财务人员熟练掌握ERP系统各个流程的具体操作方式，才能指导其他部门录入信息的准确性和及时性。同时，企业也要加强对除了财务部门以外员工的培训和指导，提高全员的综合素质。只有企业各个部门都熟悉和掌握了ERP系统，才能保证整个系统的运行更加顺畅。

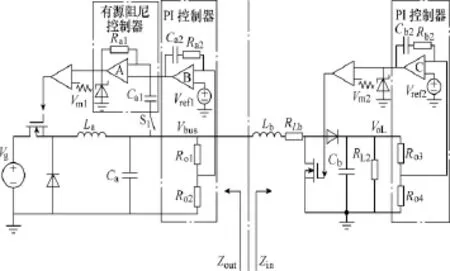
图8 Buck变换器和Boost变换器构成的级联系统Fig.8 A cascaded system consisting of a Buck converter and a Boost converter

图8 给出了 Buck变换器和Boost变换器构成的级联系统。在 Buck变换器中，运放A、电阻 Ra1和电容 Ca1构成的微分器作为有源阻尼控制器，电压闭环控制产生的调制波信号引入至微分器的同相输入端。仿真参数如表 1所示。

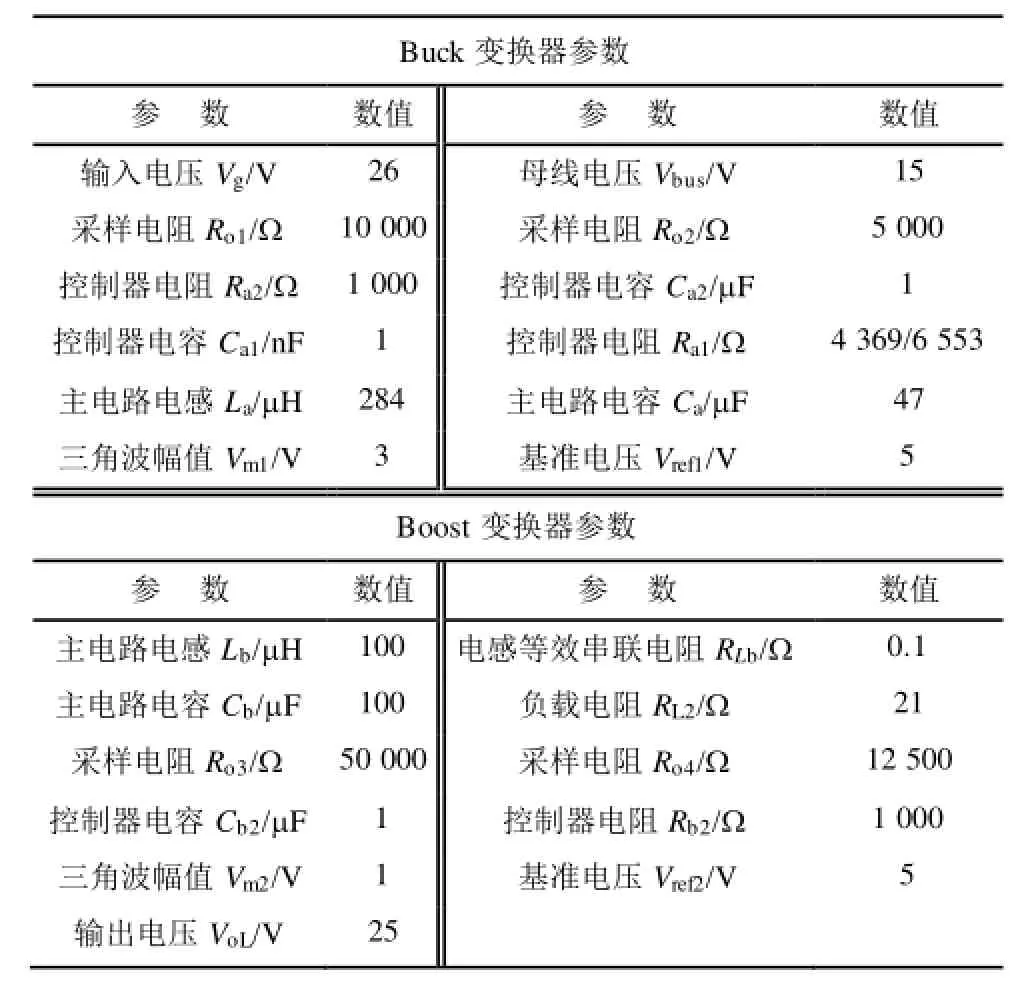
Buck变换器参数参 数 数值 参 数 数值输入电压Vg/V 26 母线电压Vbus/V 15采样电阻Ro1/Ω 10 000 采样电阻Ro2/Ω 5 000控制器电阻Ra2/Ω 1 000 控制器电容Ca2/μF 1控制器电容Ca1/nF 1 控制器电阻Ra1/Ω 4 369/6 553主电路电感La/μH 284 主电路电容Ca/μF 47三角波幅值Vm1/V 3 基准电压Vref1/V 5 Boost变换器参数参 数 数值 参 数 数值主电路电感Lb/μH 100 电感等效串联电阻RLb/Ω 0.1主电路电容Cb/μF 100 负载电阻RL2/Ω 21采样电阻Ro3/Ω 50 000 采样电阻Ro4/Ω 12 500控制器电容Cb2/μF 1 控制器电阻Rb2/Ω 1 000三角波幅值Vm2/V 1 基准电压Vref2/V 5输出电压VoL/V 25

Buck变换器的输出和Boost变换器的输出均采用比例积分（PI）控制器进行闭环调节。当S1闭合时，有源阻尼控制器工作；当 S1断开时，电阻 Ra1和运算放大器A构成电压跟随器，不会对闭环控制的调制波产生影响。由式（15）和表1可知，仿真中虚拟电阻值分别选取了 7.5Ω（Ra1=4 369Ω，Ca1= 1nF）和5Ω（Ra1=6 553Ω，Ca1=1nF）。

母线电压的仿真波形如图 9所示。当 Buck变换器不加入有源阻尼控制器时，系统不稳定。输出阻抗 Zout和输入阻抗 Zin构成的阻抗比（Zout/Zin）奈奎斯特曲线包围了（-1, j0）点，不满足奈奎斯特稳定判据，如图10所示。其输出阻抗 Zout表现出极大的峰值，阻尼特性较差，如图11所示；当Buck变换器模拟了阻值为 7.5Ω的虚拟电阻时，由图 11可知，有源阻尼控制器大幅度降低了输出阻抗，改善了其阻尼特性。但是其阻抗比构成的奈奎斯特曲线依然包含（-1, j0）点，不满足奈奎斯特稳定判据（见图 10），因此母线电压依然振荡；当 Buck变换器模拟了阻值为 5Ω的虚拟电阻时，输出阻抗进一步降低，阻尼特性得到较好改善，奈奎斯特曲线满足稳定判据，因此母线电压稳定。

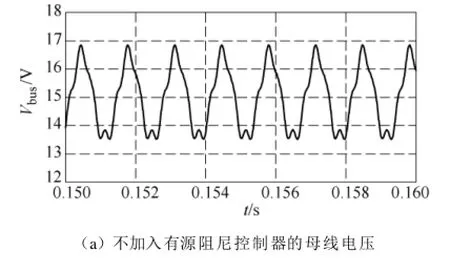
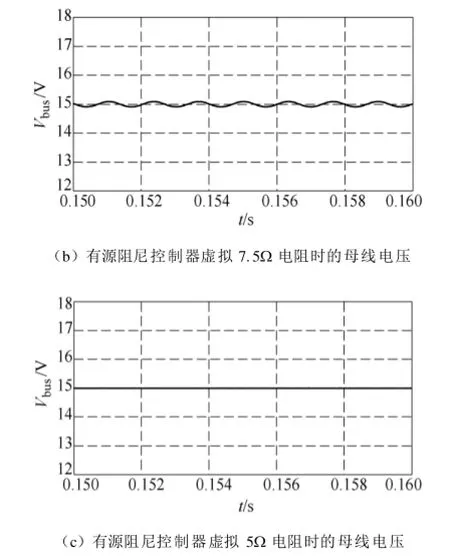
图9 级联系统的母线电压波形Fig.9 Bus voltage waveforms of the cascaded system

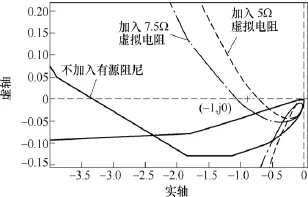
图10 阻抗比的奈奎斯特曲线（Zout/Zin）Fig.10 Nyquist plots of the impedance ratio（Zout/Zin）

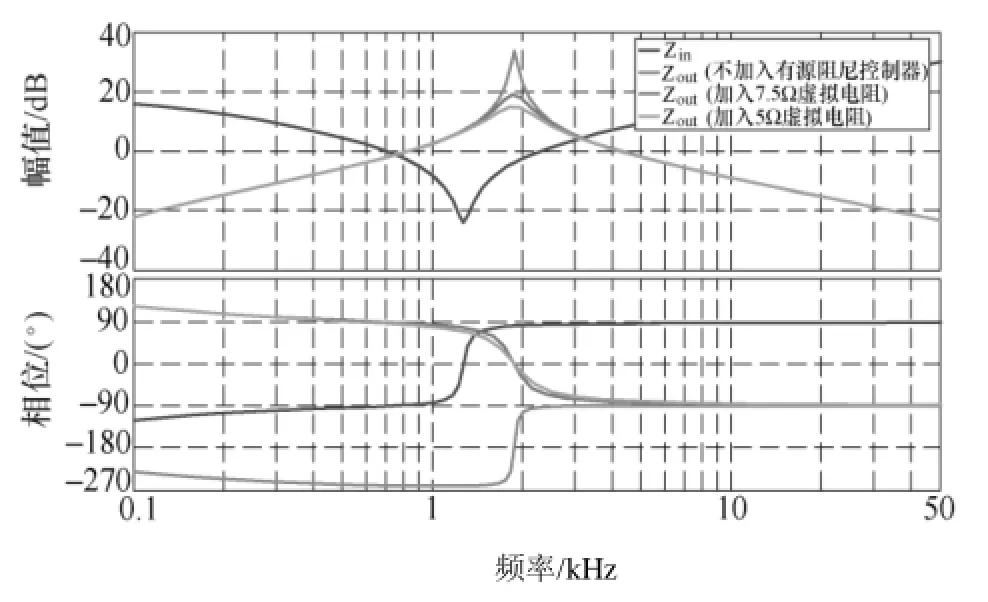
图11 级联系统中输出阻抗Zout和输入阻抗Zin的伯德图Fig.11 Zoutand Zinof the cascaded system in different situations

综上所述，在级联系统中，有源阻尼控制器可以实现源变换器的输出端并联虚拟电阻的效果，从而降低源变换器的输出阻抗，改善其阻尼特性。因此，阻抗比曲线可以随之改善以满足奈奎斯特稳定判据，达到使系统稳定的目的。

5.2 有源阻尼控制器的实验验证

实验验证分为两部分，在第一部分实验中，针对恒流负载变换器，有源阻尼控制器模拟与当前功率点对应的虚拟电阻 Rvirtual，即 Rvirtual=；第二部分实验中，有源阻尼控制器模拟与稳态功率点无关的虚拟电阻Rvirtual，即 Rvirtual≠。

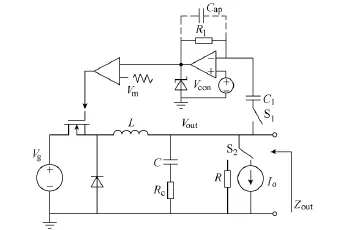
图12 采用有源阻尼控制器的Buck变换器对比实验原理图Fig.12 Comparative experiment schematic of Buck converter with active damping controller

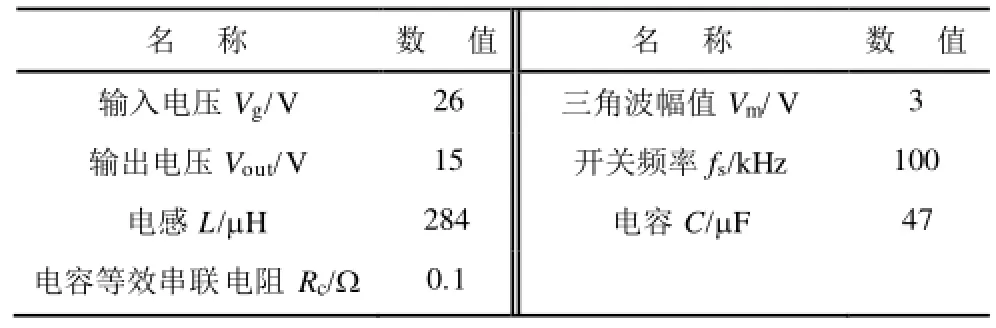
表2 主电路参数Tab.2 Circuit parameters

图 13给出了测试 Buck变换器输出阻抗的方法，该方法可适用于一般性 DC-DC变换器。图中虚线右边给出了采用网络分析仪测试输出阻抗的示意图。网络分析仪发出正弦扰动激励信号，通过隔离变压器形成电流扰动并通过电容隔离直流分量，注入至变换器的输出端口，使变换器输出端口产生相应的电压扰动信号。网络分析仪探头ch1测试输出电压扰动信号，探头ch2测试给定的电流扰动信号的负值（采用1Ω电阻进行电流采样，得到反相电流扰动信号），所以-ch1/ch2得到的幅频曲线和相频曲线就构成了变换器的输出阻抗传递函数伯德图。

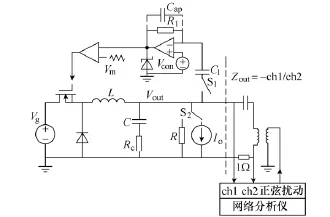
图13 测试输出阻抗的原理图Fig.13 Schematic of output impedance measurement

5.2.1 与稳态功率点相对应的虚拟电阻实验

首先进行变换器输出电压为15V时，相同功率点处不同工况的实验测试：①工况 A：变换器连接恒流负载2A；②工况B：变换器连接恒阻负载7.5Ω；③工况 C：变换器加入有源阻尼控制器（虚拟电阻7.5Ω），同时连接恒流负载2A。不同工况的实验参数如表3所示。

表3 相同功率点不同工况的实验参数Tab.3 Experiment parameters under the same power point and different working conditions

实验中工况 C的虚拟电阻 Rvirtual为 7.5Ω，等于工况B中变换器连接的电阻负载R，为了抑制干扰，加入了 2.2nF的高频极点电容Cap，极点频率约为16kHz。由于工况B与工况C的稳态工作点相同，因此在小信号模型中，变换器的输出端均等同于连接了阻值为7.5Ω的电阻，从而实现了工况B与工况C的等价（包括稳态工作点和小信号模型）。对上述三种工况的变换器输出阻抗进行测试，结果如图14所示。

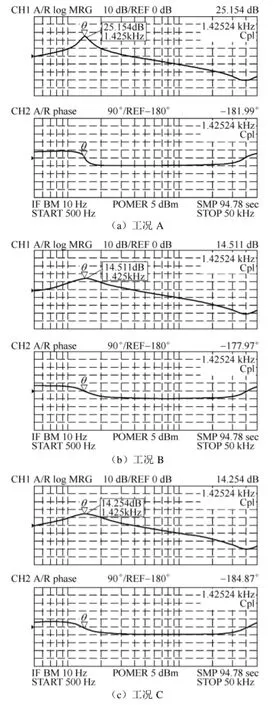
图14 相同功率点Buck变换器输出阻抗测试Fig.14 Output impedance test of Buck converter under the same power point

工况A中电路中的阻尼仅由寄生参数决定，因此具有较大的输出阻抗峰值（25.154dB），谐振频率约为1.425kHz，如图14a所示。工况B中，负载电阻提供较大的阻尼，大幅度降低了 1.425kHz时输出阻抗的峰值（14.511dB），改善了变换器输出滤波器的品质因数，如图14b所示。工况C中，其输出阻抗与工况B相同，所以图14c与图14b基本一致。因此，有源阻尼控制器实现了变换器输出端连接虚拟电阻的效果，降低了变换器的输出阻抗，改善了变换器的阻尼特性。

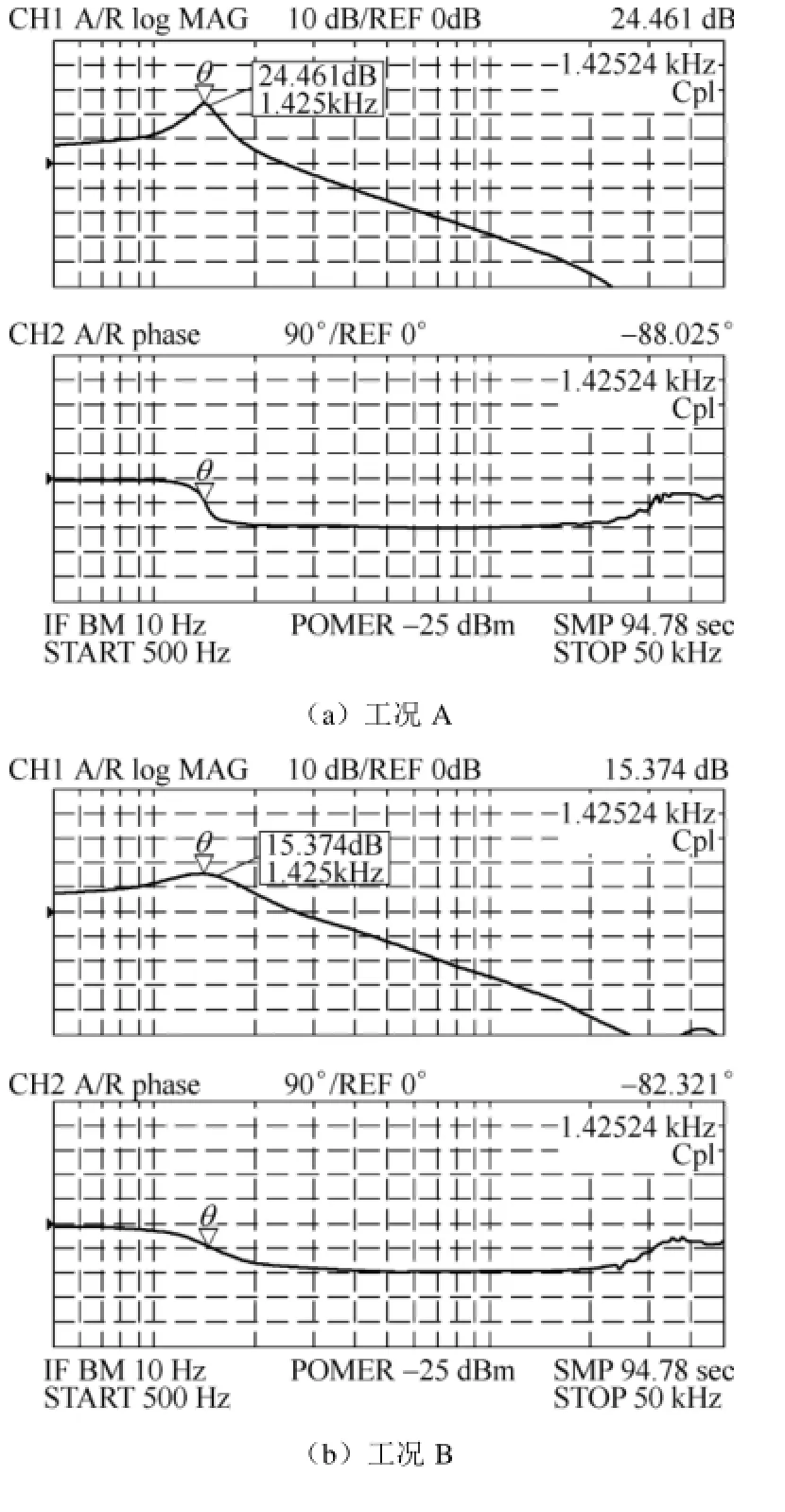
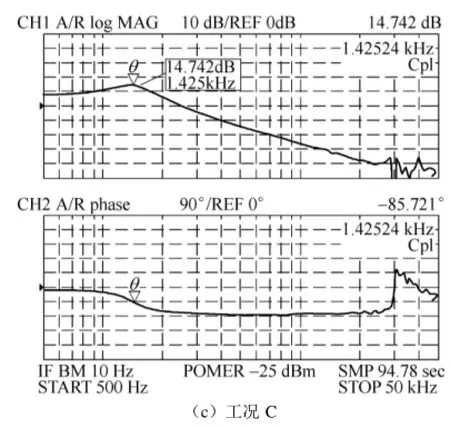
图15 不同工况的控制信号-输出电压传递函数测试Fig.15 The test results of the transfer function fromto

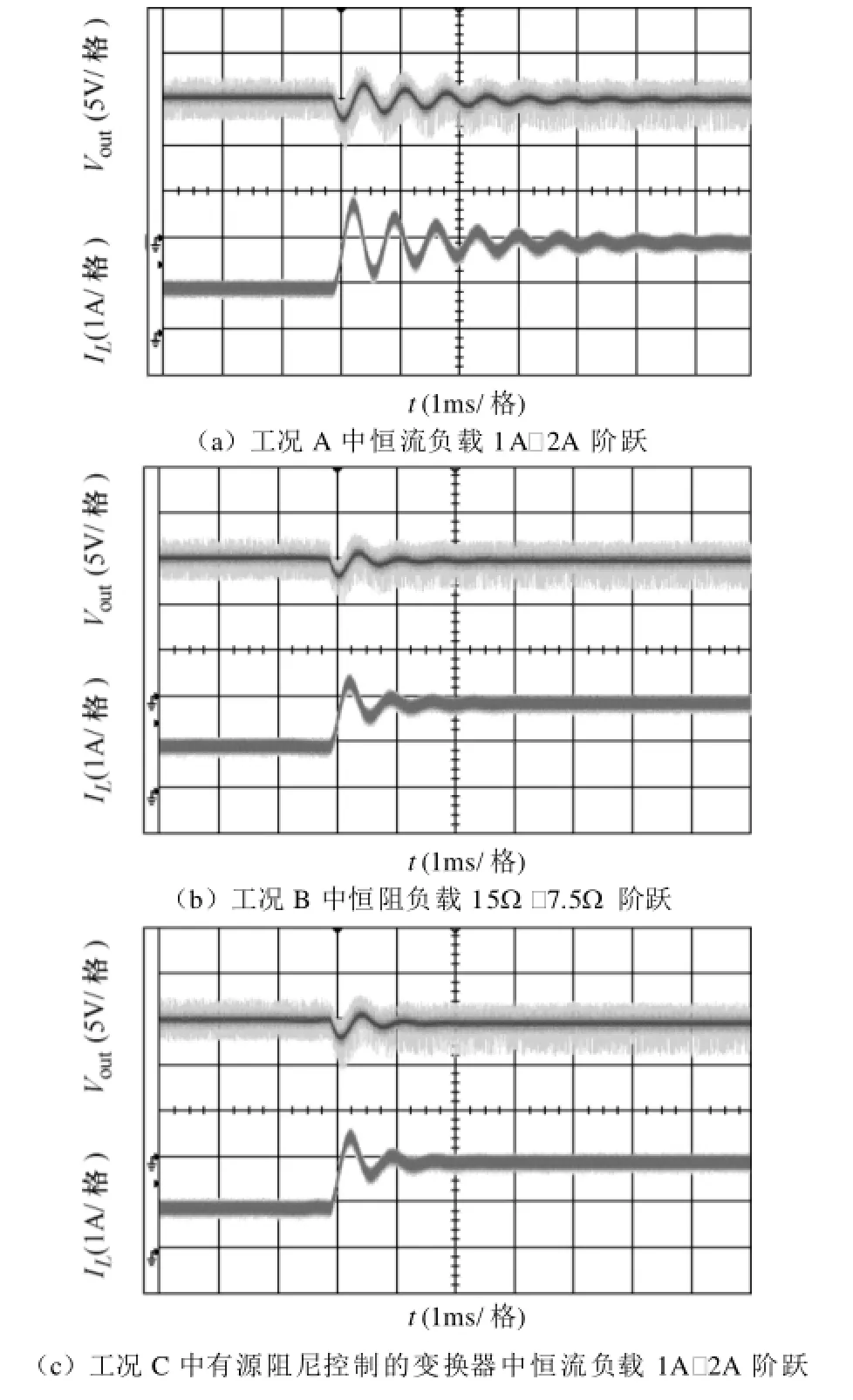
图16 Buck变换器负载的阶跃响应Fig.16 Step load response of the Buck converter

图16 给出了上述三种工况中Buck变换器进行负载阶跃时，输出电压 vout和电感电流 iL的波形。图16a表示工况A中恒流负载从1A阶跃至2A，图16b表示工况B中恒阻负载从15Ω阶跃至7.5Ω，图16c表示工况C中恒流负载从1A阶跃至2A。

由图 16a可知，由于 Buck变换器连接恒流负载，电路内部阻尼很小，因此其负载阶跃响应会产生较长时间的振荡，约为6ms。图16b和图16c中由于分别采用电阻负载和有源阻尼的方式对电路引入了阻尼，因此振荡时间较短，约为2ms。

5.2.2 与稳态功率点无关的虚拟电阻实验

变换器输出电压为15V时，进行不同功率点的实验测试，实验包括以下工况：①工况 D：变换器连接恒阻负载5Ω；②工况E：变换器连接恒阻负载15Ω并且加入有源阻尼控制器，虚拟电阻等于7.5Ω；③工况F：变换器连接恒阻负载15Ω。工况E中电路的稳态功率等于15W，负载为15Ω，由于设定的虚拟电阻为 7.5Ω，因此小信号模型的输出端等价连接了5Ω的电阻。工况D中的稳态功率等于45W，负载电阻等于5Ω，因此小信号模型的输出端电阻同样等于5Ω。虽然工况D与工况 E所对应的稳态功率点不同，但根据式（11）和式（12）可知，Buck变换器的传递函数不受稳态功率点的影响。换言之，其小信号模型的传递函数仅由其主电路参数决定。因此，工况D与工况E的小信号模型相同。工况 E中采用有源阻尼的变换器小信号模型可以通过工况D中的变换器模型进行验证。由上述分析可知，采用有源阻尼控制器可以在变换器的轻载工况中实现与重载工况等价的阻尼效果，从而降低轻载工况中变换器的输出阻抗。

不同工况的实验参数如表4所示。通过测试，得到输出阻抗和控制信号-输出电压传递函数分别如图 17、图 18所示。

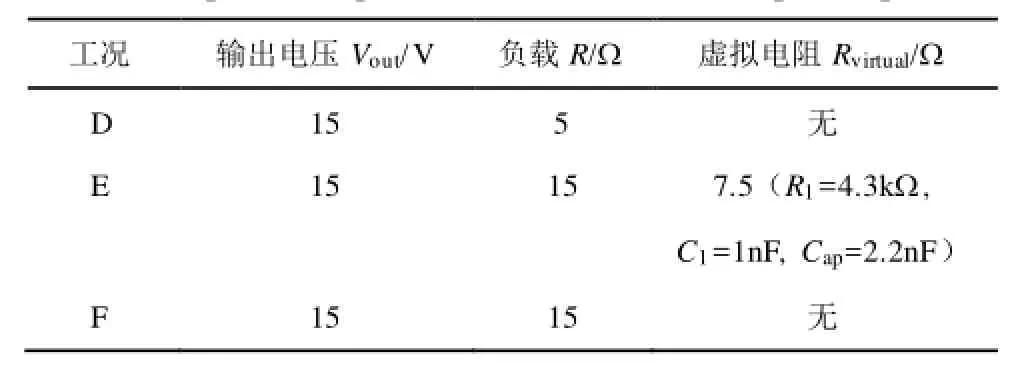
表4 不同功率点工况的实验参数Tab.4 Experiment parameters under different power points

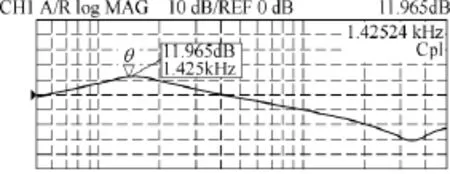
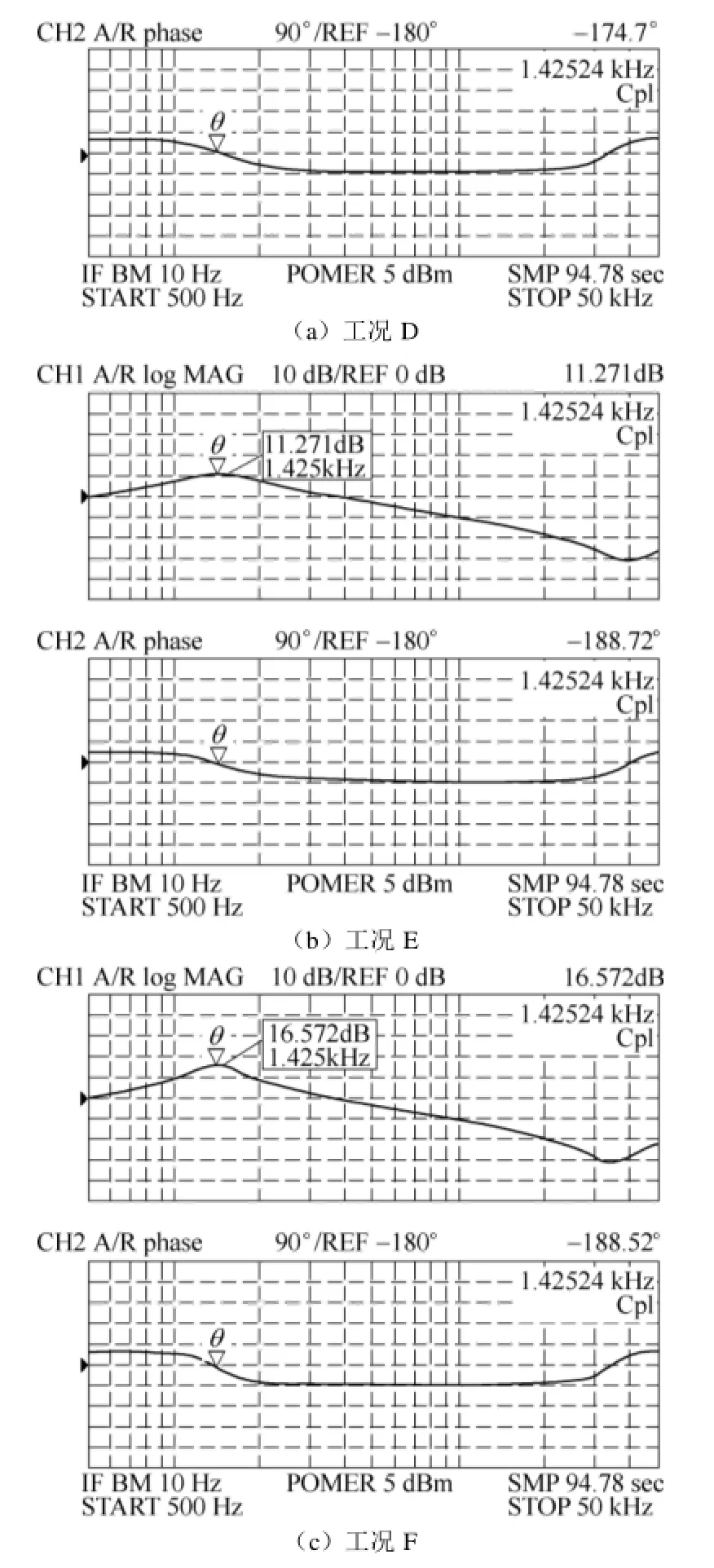
图17 不同功率点Buck变换器输出阻抗测试Fig.17 Output impedance test results of the Buck converter at different power points

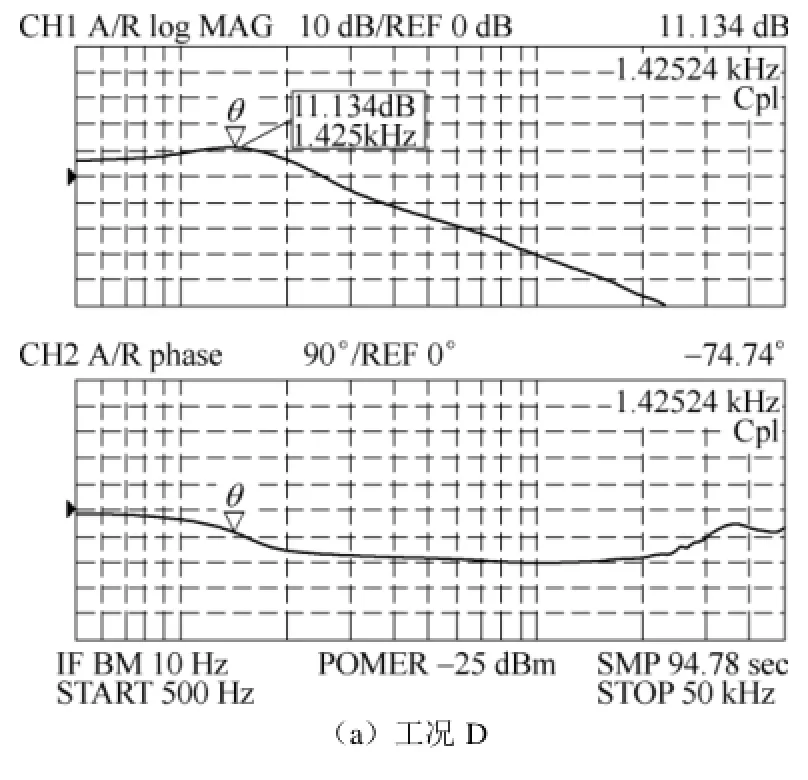
图18 不同功率点处Buck变换器的控制信号输出电压传递函数Fig.18 Transfer function test results from control signalto output voltageat different power points

工况 D中，变换器的输出阻抗在谐振频率（1.425kHz）处的幅值约为11.965dB；对于工况 E，由于变换器本身连接了15Ω恒阻负载，同时采用有源阻尼变换器模拟了 7.5Ω虚拟电阻，因此变换器小信号模型的输出端口等效连接了阻值为5Ω的电阻，在谐振频率处（1.425kHz），其输出阻抗峰值为11.271dB；工况F中变换器在谐振频率（1.425kHz）处的输出阻抗峰值为 16.572dB。

虽然功率点不同，但根据式（11）和式（12）可知，工况E与工况D的小信号模型是相同的。实际中由于变换器的寄生参数，开关管导通压降，以及电感值随稳态电流值发生变化等情况，不同的功率点会影响变换器的小信号模型，导致测试结果产生一些误差。由图17和图18可知，变换器单独连接15Ω电阻时，其模型传递函数的波特图在谐振频率处具有较高峰值。在此功率点基础上，通过模拟阻值等于 7.5Ω的虚拟电阻，大幅度降低了变换器的输出阻抗，改善了其阻尼特性，优化了其控制信号-输出电压传递函数，使其具有与连接 5Ω恒阻负载工况相似的小信号模型。

综上所述，有源阻尼控制器可以实现变换器小信号模型的输出端等效并联一个虚拟电阻，从而降低变换器的输出阻抗。虚拟电阻可以改善变换器的阻尼特性，加强其稳定性。由于虚拟电阻仅存在于小信号模型中，所以虚拟电阻值可以任意选取，而不会影响变换器的稳态工作点。这种方法仅需已知变换器的占空比-输出电压传递函数 Gvd与输出阻抗Zout，因此具有可扩展性。

6 结论

DC-DC变换器的输出阻抗是影响级联系统稳定性的重要参数。在级联系统中，源变换器的输出阻抗与负载变换器的输入阻抗决定了级联系统的稳定性。本文提出了一种适用于 DC-DC变换器的有源阻尼控制方法，能够实现变换器小信号模型的输出端并联虚拟电阻的效果，从而降低变换器的输出阻抗，改善其阻尼特性。该方法需要采样输出端电压的交流分量，因此虚拟电阻仅存在于小信号模型中，而不会影响稳态工作点。通过计算变换器模型相关的传递函数，即可得到对应的有源阻尼控制器形式。文章以 Buck变换器为例，通过仿真和实验对这种方法的有效性进行了验证。

[1] Middlebrook R D. Input filter considerations in design and application of switching regulators[C]. IEEE Proc. IAS, 1976: 366-382.

[2] Wildrick C M, Lee F C, Cho B H, et al. A method of defining the load impedance specification for a stable distributed power system[J]. IEEE Transactions on Power Electronics, 1995, 10(3): 280-285.

[3] Feng Xiaogang, Ye Zhihong, Xing Kun, et al. Individual load impedance specification for a stable DC distributed power system[C]. Applied Power Electronics Conference and Exposition, 1999, 2: 923-929.

[4] Feng Xiaogang, Ye Zhihong, Xing Kun, et al. Impedance specification and impedance improvement for DC distributed power system[C]. Power Electronics Specialists Conference, 1999, 2: 889-894.

[5] Karppanen M, Sippola M, Suntio T. Source-imposed instability and performance degradation in a regulated converter[C]. IEEE Power Electronics Specialists Conference, 2007: 194-200.

[6] 王建华, 张方华, 龚春英, 等. 电压控制型 Buck DC/DC变换器输出阻抗优化设计[J]. 电工技术学报, 2007, 22(8): 18-23.

Wang Jianhua, Zhang Fanghua, Gong Chunying, et al. Study of output impedance optimization for voltage mode control Buck DC/DC converter[J]. Transactions of China Electrotechnical Society, 2007, 22(8): 18-23.

[7] 吴涛, 阮新波. 分布式供电系统中源变换器的输出阻抗的研究[J]. 中国电机工程学报, 2008, 28(3): 66-72.

Wu Tao, Ruan Xinbo. Output impedance analysis of source converters in the DC distributed power system [J]. Proceedings of the CSEE, 2008, 28(3): 66-72.

[8] 吴涛, 阮新波. 分布式供电系统中负载变换器的输入阻抗分析[J]. 中国电机工程学报, 2008, 28(12): 20-25.

Wu Tao, Ruan Xinbo. Input impedance analysis of load converters in the distributed power system[J]. Proceedings of the CSEE, 2008, 28(12): 20-25.

[9] 姚雨迎, 张东来, 徐殿国. 级联式DC/DC变换器输出阻抗的优化设计与稳定性[J]. 电工技术学报, 2009, 24(3): 147-152.

Yao Yuying, Zhang Donglai, Xu Dianguo. Output impedance optimization and stability for cascade DC/ DC converter[J]. Transactions of China Electrotechnical Society, 2009, 24(3): 147-152.

[10] Mitchell D M. Damped EMI filters for switching regulators[J]. IEEE Transactions on Electromagnetic Compatibiliy, 1978, 20(3): 457-463.

[11] Jusoh A B. The instability effect of constant power loads[C]. Natl. Power Energy Conf., 2004: 175-179.

[12] Cespedes M, Xing L, Sun J. Constant-power load system stabilization by passive damping[J]. IEEE Transactions on Power Electronics, 2011, 26(7): 1832-1836.

[13] Redl R, Sokal N O. Near-optimum dynamic regulation of DC-DC converters using feed-forward of output current and input voltage with current-mode control [J]. IEEE Transactions on Power Electronics, 1986, 1(3): 181-192.

[14] 伍小杰, 孙蔚, 戴鹏, 等. 一种虚拟电阻并联电容有源阻尼法[J]. 电工技术学报, 2010, 25(10): 122-128.

Wu Xiaojie, Sun Wei, Dai Peng, et al. An active damping method of virtual resistor in parallel with capacitor[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 122-128.

[15] 张学广, 刘义成, 王瑞, 等. 一种新型的PWM变换器LCL滤波器有源阻尼控制策略[J]. 电工技术学报, 2011, 26(10): 188-192.

Zhang Xueguang, Liu Yicheng, Wang Rui, et al. A novel active damping control strategy for PWM converter with LCL filter[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 188-192.

[16] Hatua K, Jain A K, Banerjee D, et al. Active damping of output LC filter resonance for vector-controlled VSI-fed AC motor drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(1): 334-342.

[17] Dannehl J, Liserre M, Fuchs F W. Filter-based active damping of voltage source converters with LCL filter [J]. IEEE Transactions on Industrial Electronics, 2011, 58(8): 3623-3633.

[18] Dahono P A. A control method for DC-DC converter that has an LCL output filter based on new virtual capacitor and resistor concepts[C]. Power Electronics Specialists Conference, 2004, 1: 36-42.

[19] Rahimi A M, Emadi A. Active damping in DC/DC power electronic converters: a novel method to overcome the problems of constant power loads[J]. IEEE Transactions on Industial Electronics, 2009, 56(5): 1428-1439.

[20] Zhang X, Ruan X, Kim H, et al. Adaptive active capacitor converter for improving stability of cascaded DC power supply system[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1807-1816.

[21] Weaver W W, Krein P T. Mitigation of power system collapse through active dynamic buffers[C]. IEEE PESC, 2004: 1080-1084.

[22] Weaver W W, Krein P T. Optimal geometric control of power buffers[J]. IEEE Transactions on Power Electronics, 2009, 24(5): 1248-1258.

[23] Erickson R W. Fundamentals of Power Electronics [M]. Dordrecht, Netherlands: Kluwer Academic Publishers, 2000.

[24] Hankaniemi M, Karppanen M, Suntio T. Load-imposed instability and performance degradation in a regulated converter[J]. Electric Power Applications, 2006, 153(6): 781-786.

[25] Pengyu Jia, Trillion Q Zheng, Yan Li. Parameter design of damping networks for the Superbuck converter [J]. IEEE Transactions on Power Electronics, 2013, 28(8): 3845-3859.

[26] 陈骞, 郑琼林, 李艳. 单电感电流连续型推挽类拓扑的推衍和特性研究[J]. 中国电机工程学报, 2013, 33(6): 85-92.

Chen Qian, Trillion Q. Zheng, Li Yan. Derivation and characterization of single-inductor push-pull based topologies with continuous currents[J]. Proceedings of the CSEE, 2013, 33(6): 85-92.

An Active Damping Method to Reduce Output Impedance of Converters in Voltage Source Cascaded System

Jia Pengyu Li Yan Trillion Q Zheng

（Beijing Jiaotong University Beijing 100044 China）

In a cascaded power system, the system stability can be affected by the impedance interaction of the source converter and the load converter. Many literatures analyzed the effects on the impedance characteristics of the converter from different control methods and circuit parameters. Besides, different passive damping methods and control methods to improve the impedance characteristics of the converter are proposed to ensure the cascaded system stable. On the basis of the small signal model, an active damping method to emulate a virtual resistor, which is connected in parallel with the output of the converter’s small signal model, is presented in this paper. By this means, the output impedance of the converter can be decreased and the damping characteristics can be improved. The AC component of the output voltage needs to be sampled by the active damping controller so the steady-state operating point is not affected. Therefore, the effects caused by the impedance interaction between the source converter and load converter can be weakened. The effectiveness of this method is verified by the simulation and experiment results.

Cascaded system, DC-DC converter, output impedance, virtual resistor, active damping, stability

TM46

贾鹏宇 男，1985年生，博士研究生，主要研究方向为直流电源系统稳定性。

2013-06-25 改稿日期 2013-11-19

李 艳 女，1977年生，博士，讲师，主要研究方向为航空航天电源，多端口供电系统，光伏并网逆变器，燃料电池供电系统和荧光灯/LED驱动电源。