电动汽车用异步电机转子磁链定向校正算法研究
郭磊磊 张 兴 杨淑英 谢 震
电动汽车用异步电机转子磁链定向校正算法研究
郭磊磊 张 兴 杨淑英 谢 震
(合肥工业大学电气与自动化工程学院 合肥 230009)
异步电机参数受温度、励磁等的影响,导致基于转子磁链定向的矢量控制系统定向出现偏差。基于无功功率的算法虽然可以实现定向校正,但其校正准确度受死区的影响。为此,提出了一种改进的算法,即采用定子电流与定子磁链的点乘闭环来校正磁链定向,可以不受死区影响,提高了定向校正准确度。然而,该算法的稳态准确度受定子电感的影响,因此,设计了简单的补偿算法。理论分析和实验结果验证了该算法的有效性。
定子电流 定子磁链 点乘 死区 异步电机 电动汽车
1 引言
随着能源危机的加剧,电动汽车逐渐成为未来汽车的发展趋势。异步电机因价格低廉、维护简单而在电动汽车驱动系统中占据重要地位[1-2]。常用的异步电机矢量控制方法是直接转子磁链定向控制和间接转子磁链定向控制。两种定向方法都受电机参数的影响。为了有效解决参数对电机矢量控制定向准确度的影响问题,文献[3]设计了实用的异步电机转子磁链定向校正算法,但该算法受电机定子电阻和死区的影响。文献[4]设计了基于转子磁链q轴分量的异步电机间接矢量控制转差频率校正算法,然而该算法会导致系统运行过程中易产生振荡甚至不能正常起动,且该算法只适用于间接磁场定向控制。文献[5]提出了基于无功功率的磁场定向校正算法。该算法克服了定子电阻的影响。然而,在计算无功功率时,采用参考电压代替实际电压,受死区的影响。为此,文献[6]提出了基于无功功率的模型参考自适应转子时间常数辨识方法,通过辨识转子时间常数,实现间接磁场定向控制。为了提高准确度,加入了死区补偿算法。然而,在低速轻载的场合,经常会发生零电流钳位现象[14],电流方向判断困难,造成死区补偿偏差,并且该算法只适用于间接磁链定向控制。
为了简化异步电机矢量控制定向校正算法,提高校正准确度,本文提出了一种改进的磁链定向校正算法。该算法基于定子电流与定子磁链的点乘模型。既可用于直接转子磁链定向,也可用于间接转子磁链定向,不受定子电阻的影响,且可直接采用参考电压代替实际电压,不受死区影响。理论分析和实验结果都验证了该算法的有效性。
2 校正原理分析
基于无功功率的磁链定向校正算法[5]采用稳态无功功率作为参考模型,瞬态无功功率作为调制模型,依据模型参考自适应原理构建了异步电机磁链定向校正算法,但是该算法受死区影响,动态响应较差。为此,提出了一种改进的算法。
常用的异步电机控制方法是基于转子磁链定向的矢量控制算法,系统整体控制原理如图1虚线框外部分所示。转子位置角度计算部分通过计算转差频率和实测转速得到同步角频率,同步角频率进行积分得到矢量控制的定向角度,这是矢量控制的核心。依据定向角度并通过坐标变换,在同步旋转dq坐标系上实现矢量控制。在异步电机转子磁链定向矢量控制系统中,通常定义转子磁链位于d轴,q轴超前d轴90°。

图1 系统整体控制框图Fig.1 The overall control block diagram of the system
采用转子磁链定向控制,在定向准确时,转子磁链满足[9]


式中,ψsd、ψsq分别为d、q轴定子磁链。
定子电流与定子磁链的点乘为

由于电机参数的变化,电机定向角度常常偏于真实的转子磁链角度。在 isq>0时,定向不准主要分为定向超前和定向滞后两种情况。
当定向超前时,如图 2a所示。dq为定向准确时的转子坐标系,为定向超前时的转子坐标系。此时,估计的转子磁链位置超前于实际的转子磁链位置,这导致真实的 d轴励磁电流偏小,真实的 q轴转矩电流增大,定子电流幅值不变。由式(3)可知,此时定子磁链与定子电流的点乘偏小。定向滞后如图2b 所示。此时,估计的转子磁链位置滞后于实际的转子磁链位置,这导致真实的d 轴励磁电流偏大,真实的q 轴转矩电流偏小,定子电流幅值不变。由式(3)可知,此时定子磁链与定子电流的点乘偏大。

图2 定向超前与滞后矢量图Fig.2 Vector diagram of orientation ahead and lag
综上分析,当定向超前时,真实的定子电流与定子磁链点乘偏小,当定向滞后时,真实的定子电流与定子磁链点乘偏大。
当定向准确时,定子电流与定子磁链点乘为
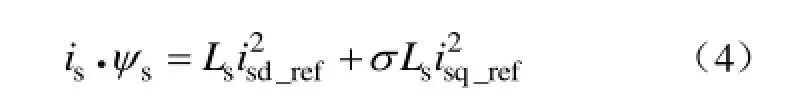

式中,ψsα、ψsβ为静止αβ坐标系上的定子磁链。
定子磁链满足
因此,可以以式(4)作为参考模型,式(5)作为调整模型,构成闭环系统实现定向校正。由式(4)可知,参考模型不受定向准确度的影响,其动态响应更好。
3 调整模型的计算
调整模型计算需要定子磁链信息。常用的磁链计算模型主要有电压模型和电流模型。电流模型受电机参数影响严重。为了尽量减小参数的影响,本文选择采用电压模型计算定子磁链,如式(6)所示。为避免使用电压传感器,本算法采用电压参考值代替实际电压值,即采用电流环 PI调节器的输出值作为电压参考值usα、usβ进行磁链计算,如图 1所示。式中,Rs为定子电阻。

然而,式(6)含有定子电阻,需要分析其对调整模型的影响。
将式(6)代入式(5)可得
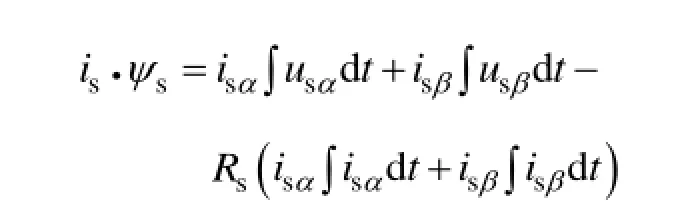

所以该算法调整模型不受定子电阻的影响。为了解决积分问题,本文采用文献[7]设计的采用低通滤波器代替积分并进行补偿的算法。此外,调整模型的计算需要定子电压,在实际系统中,通常采用参考电压代替实际电压,但这会受到死区的影响[5]。为此,需要分析死区对本算法调整模型计算的影响。
假设控制的开关周期为 Ts,死区时间为 t,直流侧电压为 Udc,不考虑开关过程及管压降时,真实的电压和参考电压的关系可表示为[10]

考虑abc到αβ的坐标变换,易得


其中


可见,该算法调整模型采用参考电压计算,结果与采用实际电压相同,即该算法调整模型不受死区影响。因此,该算法可提高定向校正准确度。
4 定向校正系统分析
4.1 动态响应分析
图3给出了定向超前时的定子电流矢量图。
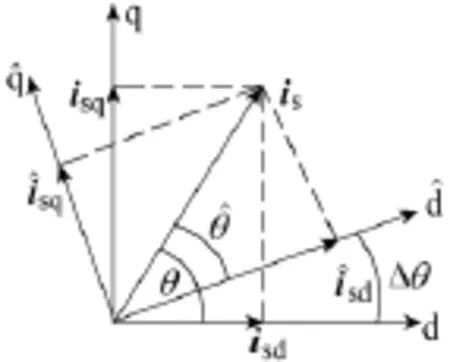
图3 定子电流矢量图Fig.3 Stator current vector diagram
由图3可得

根据三角函数和差化积公式得

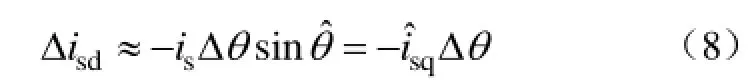


在dq坐标系下分析误差的动态响应。定义误差为
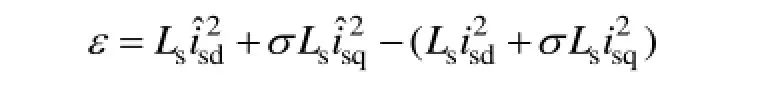



3.2 稳态准确度分析
如式(7)所示,调整模型不受电机参数的影响。由以上分析可知,调整模型计算不受死区的影响。因此,可认为该算法调整模型对校正系统的稳态准确度没有影响。
由式(4)易知,参考模型含有电感参数。当参
由式(11)可知,在数发生变化时,导致实际参考模型发生变化,而控制系统中如果采用固定的参数,将会导致调整模型收敛于一个错误的值,给定向带来偏差。假设定子电感额定值为Ls,由于运行条件的变化导致其实际值增大为 Ls+ΔLs,漏感σLs很小,可认为不变化。由于实际调整模型要根据式(7)计算,不依赖于定子电感。当闭环系统稳定时,调整模型收敛于错误的参考模型,ε=0。这时,因参考模型参数发生变化导致的误差εL为

综合以上动态与稳态分析,得到如图 4a所示的闭环校正系统框图。

图4 闭环校正系统及具体实施框图Fig.4 Closed-loop correction system and specific implementation diagram
在恒磁通控制时,励磁电感不变,εL=0。当ε>0时,控制使Δθ<0,经过PI调节器减小ε;当ε<0时,控制使Δθ>0,经过PI调节器增大ε,最终使ε收敛于零。然而,在电动汽车驱动场合,常常采用变磁链控制,导致励磁电感变化[12],。当εL>0时,参考模型偏大,稳态时应当使ε=εL>0,才能保证定向得到正确校正,反之控制使ε=εL<0。因此,如果要精确控制,必须已知εL。为了得到励磁电感参数,文献[8]、文献[12-13]研究了励磁电感在线辨识算法,然而在线辨识算法的引入,增加了系统的运算量,提高了系统对控制器的要求。当忽略εL时,必然给控制系统带来误差。为了校正定子电感对参考模型的影响,简化算法,实现准确定向,本文采用离线参数辨识[11]方法辨识得到励磁电感和漏感,通过拟合曲线方法得到励磁电感与励磁电流的关系。同时,考虑漏感不变,可得到。
由以上分析可得定向校正环节的具体实施框图见图4b。
综上,本算法的整体控制框图见图 1。图中虚线框内部分为本文提出的定向校正环节。定向出现偏差时,定向校正环节自动实现矢量控制系统的定向校正。
5 实验结果
实验中采用15kW 笼型异步电机,其额定电压为180V,额定电流为80A,额定频率为120Hz,极对数为 2。采用 DSP28335构成控制器。开关频率为2kHz,死区时间为6μs。采用间接矢量控制算法。离线辨识得到转子时间常数为 0.186。图 5给出了不同转子时间常数下空载运行时的实测 V-F曲线,给定额定励磁电流为35A。

图5 空载实测V-F曲线Fig.5 V-F curve of no-load
为了验证空载时电机电压为定向准确时的电机电压,人为选择两个错误的转子时间常数进行空载试验,并与采用准确时间常数的实验结果进行对比(见图5)。可见,对于不同的转子时间常数,其输出电压基本相等。这是由于空载条件下转矩电流很小,转差频率很小造成的。说明空载时电机端电压可代表定向准确时的电机端电压。加载时,如果定向准确,则电机电压应保持空载时的电压值基本不变。
图6给出了负载电流为21.9A时的加闭环和不加闭环时的实测V-F曲线。可见,不加闭环时,定向偏差严重。这主要是因为电机转子时间常数不仅受温度、励磁饱和的影响,还受频率等其他非线性特性的影响。加闭环后,电机输出电压等于空载时的电机电压,定向得到校正。

图6 有闭环和无闭环V-F曲线对比Fig.6 Comparison of V-F curve with and without closed-loop
基于无功功率的算法受死区的影响,因而定向校正准确度受到限制。图7比较了本算法和基于无功功率算法的磁链定向校正效果。图 7a对应转矩电流为28.4A,图7b对应转矩电流为59A。可见由于基于无功功率的算法受死区的影响,导致参考模型大于真实值,造成定向超前,励磁电流偏小,电机电压偏小。本算法则较好地实现了定向校正。
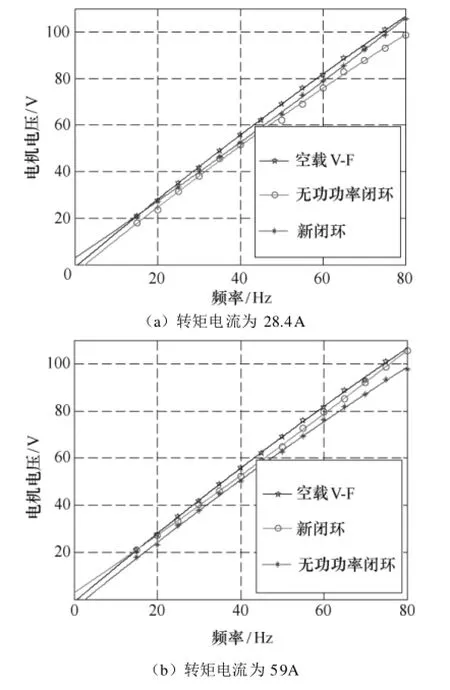
图7 新闭环和无功功率闭环V-F曲线对比Fig.7 Comparison of V-F curve based on the new closedloop system and the reactive power closed-loop system
图 8a给出了转子时间常数为 0.186时,不同频率下随负载增加电机端电压的变化曲线。从下到上,频率从15Hz以5Hz间隔增加到80Hz。可见,随着负载的增加,电机端电压降低,说明定向不准。图8b给出了加入校正环后的对应曲线。可见加入校正环后,系统的定向准确度大大提高。
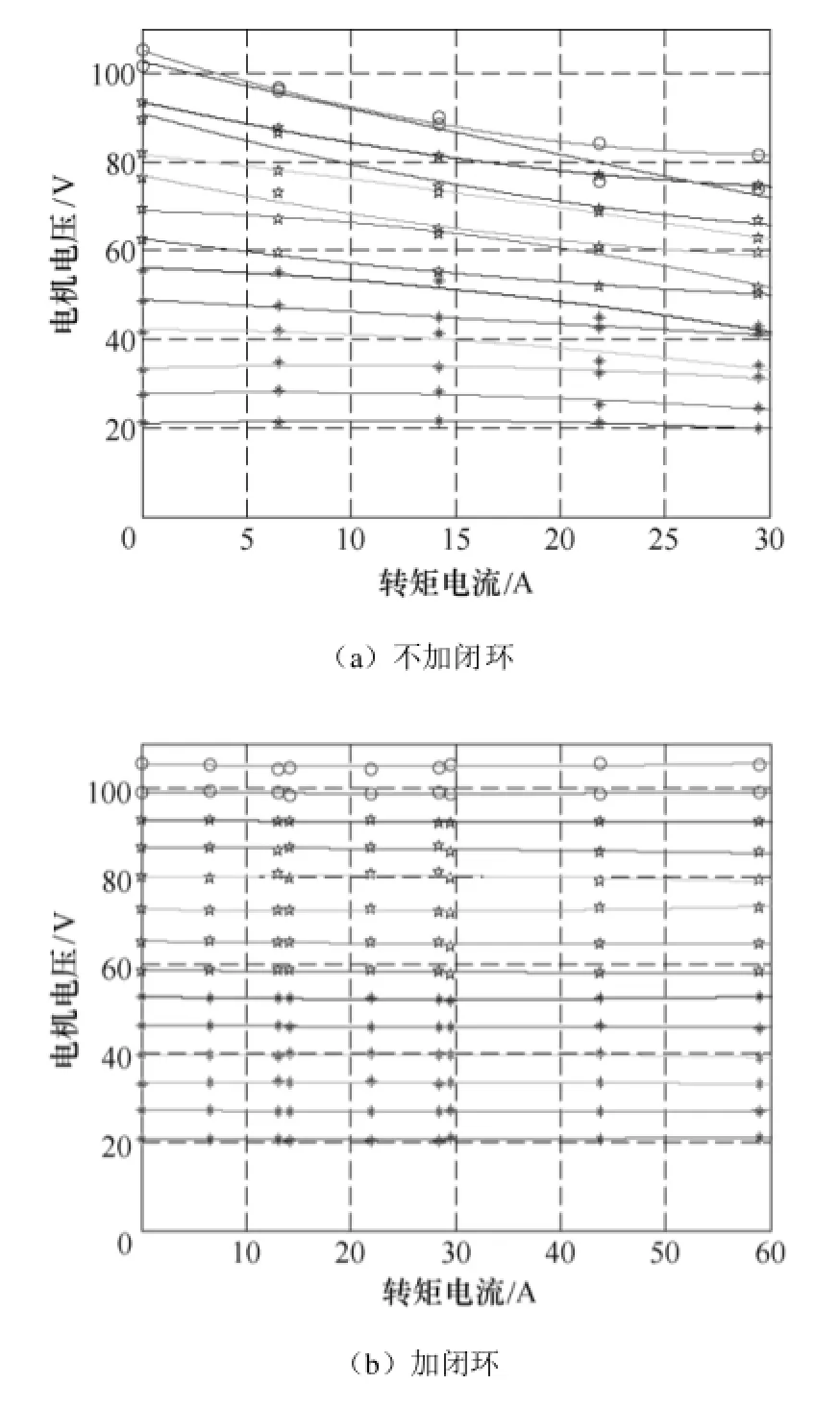
图8 不加闭环和加闭环时的电压曲线Fig.8 Voltage curve without and with closed-loop system
弱磁运行时,因为励磁电感会受到影响,从而影响该定向校正算法,而开环弱磁也会影响励磁电感,又考虑到实验平台的限制,本文采用开环弱磁的方法验证该算法的有效性。
图9a给出了励磁电流为24A时的 V-F曲线,转矩电流为 21.9A。理想 V-F曲线是根据同一转速时,励磁电流与电机电压成正比来近似得到。图9b给出了励磁电流为 12A时的 V-F曲线。可见,不加校正时,定向出现偏差,加入校正后,偏差得到校正。校正后的V-F曲线与理想 V-F曲线存在差别,主要是因为电机定子电阻的压降及非线性特性引起的。

图9 弱磁时的V-F曲线Fig.9 V-F curve with flux-weakening
为了验证该算法的动态响应性能,图 10给出了励磁电流由 35A突减为 24A时的动态响应波形。由于励磁电流突减,参考模型突减,调整模型可以实现稳定地跟踪,系统具有良好的动态响应性能。

图10 系统动态响应波形Fig.10 Dynamic response waveforms of the system
6 结论
本文设计了一种改进的转子磁链定向校正算法,解释了其校正原理,研究了死区对该算法的影响,设计了闭环校正系统,实验结果表明,本算法不受死区影响,可进一步提高定向校正准确度。
附录
考虑到sgn(Icosωt)=sgn(cosωt),而cosωt是周期为2π的周期偶函数,则sgn(cosωt)是周期方波偶函数。sgn(cosωt)傅里叶展开后得到

则
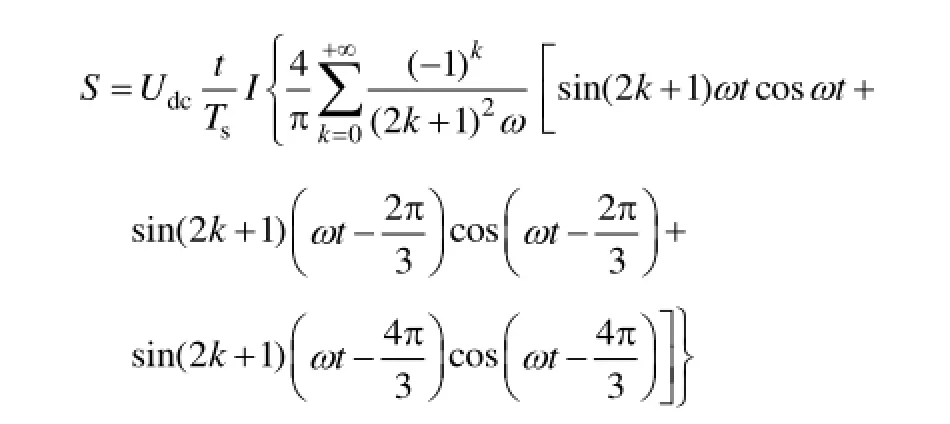
定义

采用积化和差方程

得到
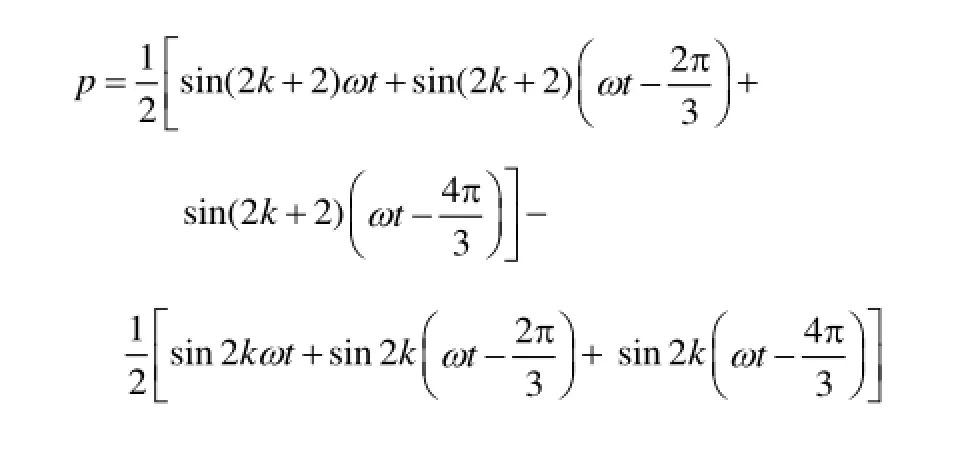
分别分析 k=0,3n,3n-1,3n-2(n=1,2,…),并考虑到
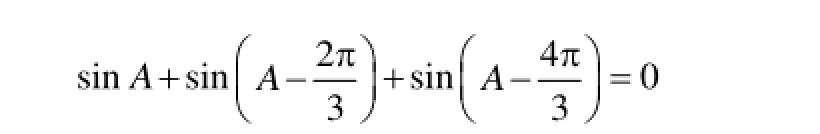
最后可得 p在周期(0,2π/ω)内平均值为 0,所以 S在周期(0,2π/ω)内平均值为0。
[1] 张细政, 王耀南, 杨民生. 电动车用感应电机电阻的状态滑模观测新方法[J]. 中国电机工程学报, 2009, 29(15): 101-106.
Zhang Xizheng, Wang Yaonan, Yang Minsheng. State sliding-mode observer based resistance estimation of induction motors for electric vehicle[J]. Proceedings of the CSEE, 2009, 29(15): 101-106.
[2] 陈勇, 张大明, 姜丕杰. 电动汽车用异步电机矢量控制系统仿真分析[J]. 系统仿真学报, 2007, 19(16): 3761-3765.
Chen Yong, Zhang Daming, Jiang Pijie. Simulation analysis of vector control system for asynchronous motor in electric vehicles[J]. Journal of System Simulation, 2007, 19(16): 3761-3765.
[3] 孙大南, 刘志刚, 刁利军, 等. 牵引电机矢量控制转子磁场准确定向实时校正策略[J]. 电工技术学报, 2011, 26(9): 116-123.
Sun Danan, Liu Zhigang, Diao Lijun, et al. Accurate rotor flux orientation real-time correction strategy for vector control of traction motors[J]. Transactions of China Electro Technical Society, 2011, 26(9): 116-123.
[4] 樊扬, 瞿文龙, 陆海峰, 等. 基于转子磁链q轴分量的异步电机间接矢量控制转差频率校正[J]. 中国电机工程学报, 2009, 29(9): 62-66.
Fan Yang, Qu Wenlong, Lu Haifeng, et al. Slip frequency correction method base on rotor flux qAxis component for induction machine indirect vector control system[J]. Proceedings of the CSEE, 2009, 29(9): 62-66.
[5] 陆海峰, 瞿文龙, 张磊, 等. 一种基于无功功率的异步电机矢量控制转子磁场准确定向方法[J]. 中国电机工程学报, 2005, 25(16): 116-120.
Lu Haifeng, Qu Wenlong, Zhang Lei, et al. A novel rotor flux oriented scheme of induction motor based on reactive power[J]. Proceedings of the CSEE, 2005, 25(16): 116-120.
[6] 王高林, 杨荣峰, 张家皖, 等. 一种感应电机转子时间常数MRAS的在线辨识方法[J]. 电工技术学报, 2012, 27(4): 49-53.
Wang Gaolin, Yang Rongfeng, Zhang Jiawan, et al. Rotor time constant on-line estimation of inductionmotors based on MRAS[J]. Transactions of China Electro Technical Society, 2012, 27(4): 49-53.
[7] Mihai Comanescu, Longya Xu. An improved flux observer based on PLL frequency estimator for sensorless vector control of induction motors[J]. IEEE Trans. on Industrial Electronics, 2006, 53(1): 50-56.
[8] Emil Levi, Matija Sokola, Slobodan N Vukosavic. A method for magnetizing curve identification in rotor flux oriented induction machines[J]. IEEE Trans. on Energy Conversion, 2000, 15(2): 157-162.
[9] 陈伯时. 电力拖动自动控制系统[M]. 3版. 北京:机械工业出版社, 2008.
[10] 王高林, 于泳, 杨荣峰, 等. 感应电机空间矢量PWM 控制逆变器死区效应补偿[J]. 中国电机工程学报, 2008, 28(15): 79-83.
Wang Gaolin, Yu Yong, Yang Rongfeng, et al. Deadtime compensation of space vector PWM inverter for induction motor[J]. Proceedings of the CSEE, 2008, 28(15): 79-83.
[11] 刘洋, 赵金, 王庆义. 间接矢量控制系统中的异步电动机参数辨识[J]. 电工技术学报, 2008, 23(7): 22-26.
Liu Yang, Zhao Jin, Wang Qingyi. An off-line parameter identification method for indirect vector controlled induction motor drive[J]. Transactions of China Electro Technical Society, 2008, 23(7): 22-26.
[12] Dae Hee Choi, Soon Bong Cho, Dong Seok Hyun. Improved torque response by tuning of the magnetizing inductance under field weakening operation region [C]. Industry Applications Conference, New Orleans, Louisiana, 1997.
[13] Mohamed S Zaky, Mahmoud M Khater, Shokry S Shokralla. Wide-speed-range estimation with online parameter identification schemes of sensorless induction motor drives[J]. IEEE Trans. on Industrial Electronics, 2009, 56(5): 1699-1707.
[14] 胡庆波, 吕征宇. 一种新颖的基于空间矢量 PWM的死区补偿方法[J]. 中国电机工程学报, 2005, 25(3): 13-17.
Hu Qingbo, Lü Zhengyu. A novel method for deadtime compensation based on SVPWM[J]. Proceedings of the CSEE, 2005, 25(3): 13-17.
Research on Induction Motor Rotor Flux Orientation Correction Algorithm for Electric Vehicles
Guo Leilei Zhang Xing Yang Shuying Xie Zhen
(Hefei University of Technology Hefei 230009 China)
The parameters of induction motor are affected by temperature, field current and so on, which result in oriented deviation in the rotor flux oriented vector control. Although the algorithm based on reactive power can realize orientation correction, the correction accuracy is affected by the dead zone. Therefore, a modified method is proposed, which based on a closed-loop controller in terms of the dot product of stator current and stator flux. This method is independent of the dead zone and so the orientation correction accuracy is improved. However, the steady-state accuracy is affected by the stator inductance. Hence, a simple compensation algorithm is designed. The theoretical analysis and experimental results verify the effectiveness of the proposed algorithm.
Stator current, stator flux, dot product, dead zone, induction motor, electric vehicle
TM343
郭磊磊 男,1987年生,博士研究生,主要研究方向为大功率风力发电系统驱动技术等。
国家“十二五”科技支撑计划项目(2012BAA01B04)。
2013-01-21 改稿日期 2013-03-14
张 兴 男,1963年生,教授,博士生导师,主要研究方向为电力电子与电力传动和新能源技术等。

