集磁式OCS磁特性随温度变化的研究
李 超 王夏菁 徐启峰
集磁式OCS磁特性随温度变化的研究
李 超 王夏菁 徐启峰
(福州大学电气工程与自动化学院 福州 350108)
温漂问题是制约集磁式光学电流传感器实用化的瓶颈之一,目前研究集中在光学器件温度特性分析与补偿方面,缺乏对传感头磁特性随温度变化的分析。实际应用中磁导率和气隙长度随温度变化,使气隙磁场强度改变并影响测量准确度,因此有必要对传感头磁特性随温度变化情况进行分析。本文分析了铁磁材料磁滞回线随温度变化的情况,并在J-A模型的基础上建立带温度系数的磁滞模型;提出热膨胀系数和磁致伸缩系数的近似表达式,修正了热膨胀和磁致伸缩对气隙长度的影响;最后建立集磁环附加温度参数和气隙参数的磁滞模型,分析磁特性随温度变化情况。基于该模型提出一种具有稳定温度特性的传感头设计方法,以铁基非晶合金为例进行了仿真和实验验证,二者结果吻合,证明了模型和设计方法的有效性。
光学电流传感器 温度 Jiles-Atherton模型 磁滞回线 集磁环 铁磁材料 气隙
1 引言
光学电流传感器与传统电磁式电流互感器相比,具有绝缘性能好、响应频带宽、体积小和信号数字化等优势[1],但由于温漂和线性双折射等问题,长期以来未能实现商业运行[2]。因此温度特性是目前OCS研究的重点内容之一。
近年来人们对 OCS的温度特性进行了深入研究,如文献[3]分析了 1/4波片的温度特性,文献[4]分析了磁光材料的 Verdet常数和双折射的温度特性,文献[5]提出了在数据采集侧的温度补偿方法等。以上研究主要集中在光学器件的温度特性分析和二次电路温度补偿方面,缺乏对 OCS磁特性随温度变化的分析。集磁式OCS挂网运行时环境温度变化范围较大,一方面使铁磁材料磁导率发生变化;另一方面气隙长度由于热膨胀和磁致伸缩的影响发生变化,最终导致作用于磁光材料的磁场强度随温度发生改变,影响测量准确度。目前尚没有文献分析气隙磁场强度随温度变化情况,因此有必要对集磁式OCS磁特性随温度变化情况进行研究,研究内容包括铁磁材料磁滞回线随温度的变化,气隙长度随温度、磁场的变化,气隙、磁滞回线和温度之间的耦合作用等。
本文首先介绍了铁磁材料磁滞回线的温度特性,并在 J-A(Jiles-Atherton)模型基础上建立了带温度系数的磁滞模型;分析了磁致伸缩和热膨胀对气隙长度的影响,提出磁致伸缩系数和热膨胀系数的近似公式,进而修正气隙长度值;最终建立了集磁式OCS带温度系数和气隙参数的磁场模型,完成了磁特性随温度变化的仿真;最后,结合非晶合金材料磁特性与温度特性,提出了一种具有稳定温度特性的传感头设计方案。实验结果表明仿真模型与设计方案是正确的。
2 集磁式OCS工作原理分析
集磁式 OCS将一个开气隙的磁环套在载流母线上,磁光材料放置在气隙中,激光信号通过光纤传输至气隙,经过反射棱镜、起偏器、磁光材料、检偏器和光电接收单元检测得到电流。采用硅钢片和非晶合金等铁磁材料作为集磁环可以加强气隙中作用于磁光材料的磁场强度,提高测量灵敏度[6]。集磁式OCS的基本原理是法拉第磁旋光效应,即当一束线偏振光通过置于磁场中的磁光材料时其偏振面发生旋转,旋转的角度即法拉第旋转角为

式中,H为磁场强度;l为磁光材料沿磁场方向的通光路径长度;V为磁光材料Verdet常数。
从式(1)可知,当磁光材料与光路设计确定后,法拉第旋转角与磁场强度成正比。
集磁式OCS传感头结构如图1所示,其中集磁环的平均周长为 L,铁磁材料的磁路长度为 Lcore,气隙长度为 Lgap。磁光材料处于集磁环气隙中,气隙中磁场强度的大小直接决定法拉第旋转角的大小。由于气隙平滑且与磁力线方向垂直,可以不考虑漏磁等问题,认为气隙长度 Lgap就是气隙中平均磁力线的长度,集磁环气隙处的磁感应强度与磁心横截面上的磁感应强度相同。
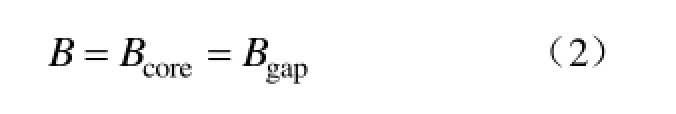
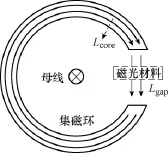
图1 集磁式OCS结构Fig.1 Structure of OCS with magnetic concentrator
由安培环路定理,将励磁电流折算到一匝,得
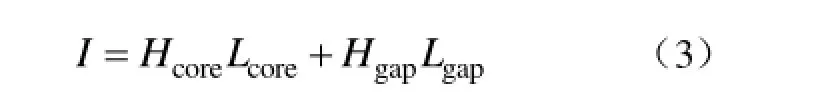
磁感应强度有
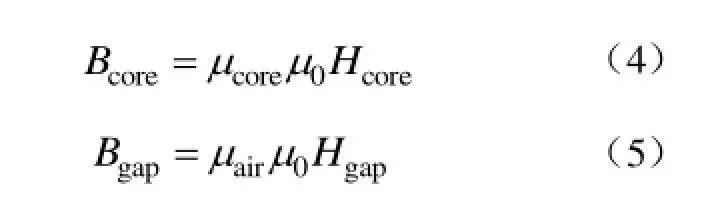
将式(2)、式(4)和式(5)代入式(3),得
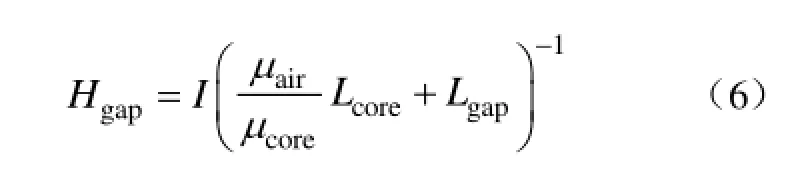
通常认为μcore为一常数,且远大于空气相对磁导率μair,同时认为气隙长度固定不变,将式(6)简化为

由式(1)和式(7)可知,法拉第旋转角与一次电流成正比,通过测量法拉第旋转角可实现一次电流测量。而温度对集磁式OCS磁特性的影响体现在以下几个方面:
(1)铁磁材料磁导率随温度变化。
(2)热胀冷缩导致气隙长度变化。
(3)磁致伸缩导致气隙长度变化,而磁致伸缩系数随温度改变。
本文建立了磁导率 μcore和气隙长度 Lgap随温度变化的数学模型和带温度与气隙系数的磁模型,藉此实现集磁式OCS磁特性随温度变化的分析。
3 传感头磁与温度特性分析
3.1 铁磁材料磁滞回线温度特性分析
通过对多种铁磁材料的实验研究,证明磁导率会随温度变化,以其温度特性的不同可以将铁磁材料分为两类:①硅钢片、坡莫合金、电工纯铁和铁氧体等;②纳米晶和非晶合金。以硅钢片和非晶合金为例,其最大磁导率的温度特性如图2所示。硅钢片的最大磁导率随温度上升而减小。而非晶合金的温度特性较复杂,随着温度的上升,非晶合金磁导率增大,上升至一定温度后磁导率达到最大值,定义此温度为 Tb;随着温度的继续上升,磁导率减小;到达居里温度 Tc附近时,磁导率急剧下降,接近于零[7-8]。
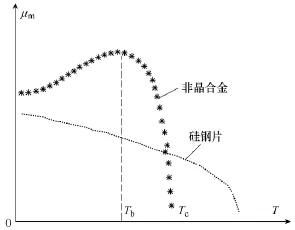
图2 最大磁导率随温度变化曲线Fig.2 Variation of maximum magnetic permeability with temperature change
为得到不同磁场强度、不同温度下磁导率的连续表达式,需要建立磁滞回线的数学模型。本文选取磁滞建模领域较经典的J-A模型对各种铁磁材料进行建模。J-A 理论认为非磁性夹杂、晶界和内应力等牵制点的存在使畴壁取代的磁化过程受阻而导致磁滞[9-10],并将磁化强度分解为不可逆磁化分量Mirr和可逆磁化分量 Mrev两部分[11-12],即
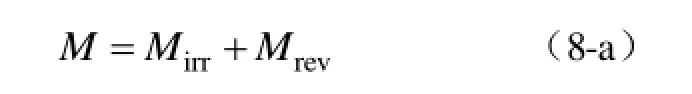
不可逆分量、可逆分量可分别由下式表示:
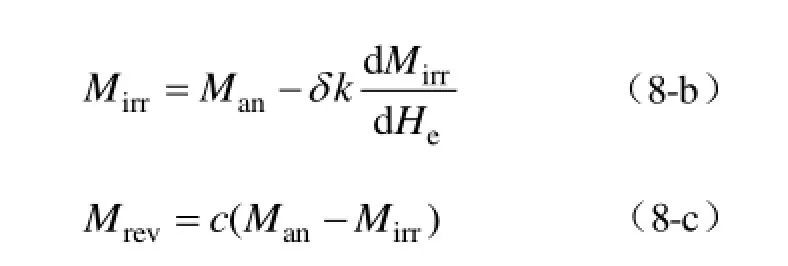
其中,Man为非磁滞磁化曲线,其计算式为
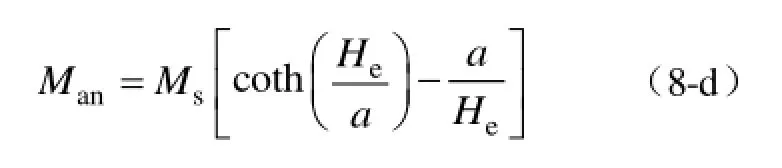
He为有效磁场强度,计算式为

Ms、c、a、k、α为J-A模型的5个参数,联立式可推导出M-H的关系式为
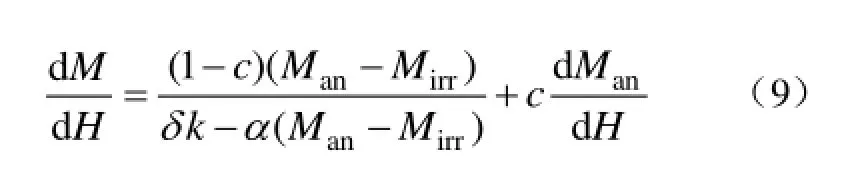
文献[13]详细分析了 J-A模型 5个参数对磁滞回线的影响:最大磁化强度只由Ms确定;矫顽力受k、c共同影响,矫顽力点和剩磁点的斜率受a、α、Ms影响。因此可通过修改模型参数引入温度系数,实现对磁滞回线温度特性的仿真。
文献[14-15]根据平均场理论对镍的最大磁化强度进行了温度修正,引入了临界指数和温度等参数。根据文献[13-15]的研究内容,在此新提出了通过修正J-A模型参数引入临界指数和温度等参数的方法,弥补了J-A模型无法对温度特性进行仿真的不足。
由于硅钢片等材料与非晶合金、纳米晶材料的温度特性差异较大,需要分别对两类材料进行模型参数的修正。
(1)根据文献[14-15]中平均场理论引入临界指数和温度参数,提出硅钢片等铁磁材料的J-A模型参数修正公式
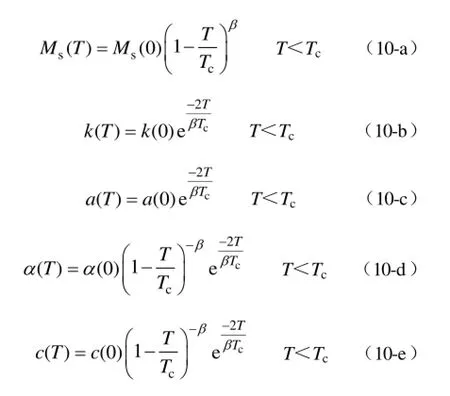
为方便模型的建立,设常温为 T0,常温下 J-A模型参数分别为 Ms(T0)、c(T0)、a(T0)、k(T0)、α(T0),此时由式(10-a)可得
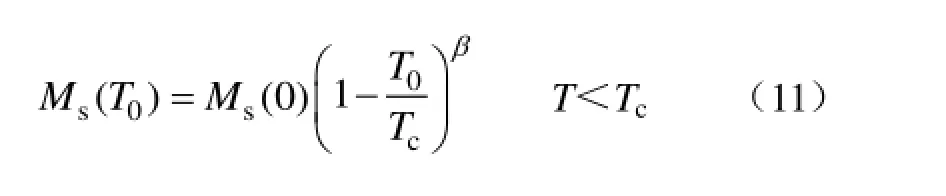
由式(10-a)和式(11)联立可得
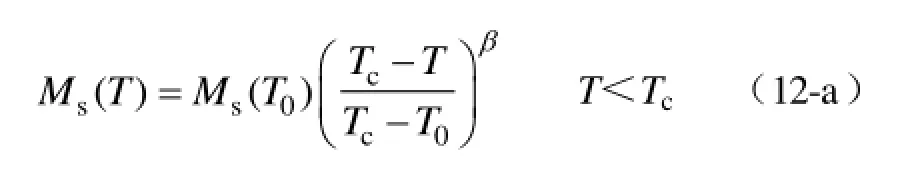
同理将式(10)中的J-A模型其他参数的修正公式转换为以室温为基准的式(12)。
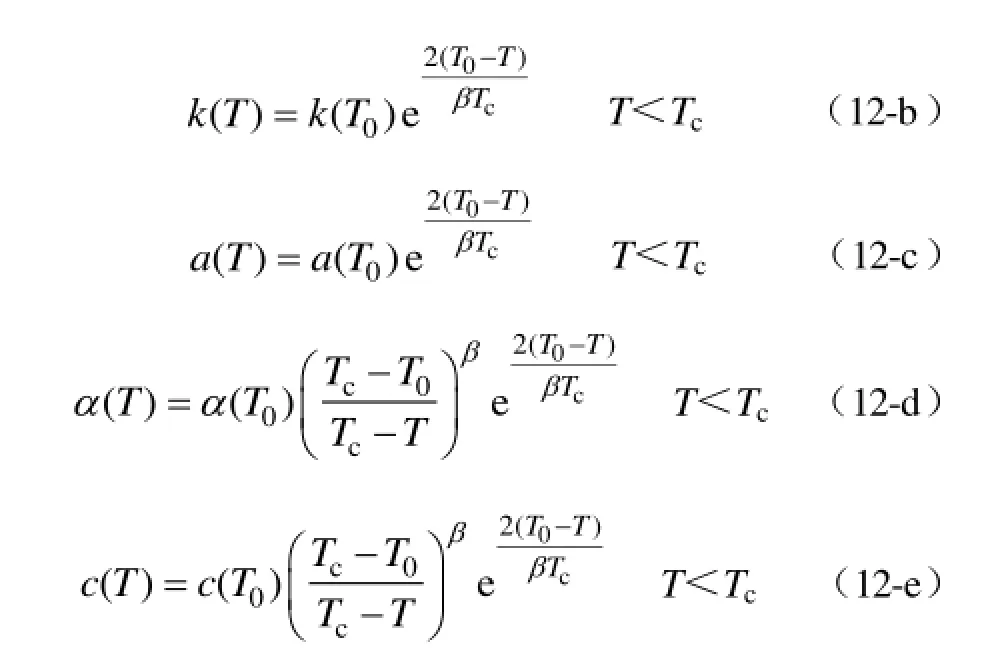
居里温度Tc与临界指数β的确认是J-A模型温度修正的关键。Tc的测量方法有很多,例如 Ms-T曲线法、感应法、起始磁导率-温度曲线法和磁电阻效应法等[16]。目前通过物理性能测试仪 PPMS测量Ms-T曲线的方法最为精确,即通过图2中的曲线确认Ms接近零时的温度即为此材料的居里温度。
临界指数β可通过测量室温与非室温度条件下的两条 M-H曲线来确定。由室温下 M-H曲线得到Ms,其他温度下的 M-H曲线得到 Ms(T),代入式(12-a)得到初始的临界指数 β。这个指数存在一定的误差,需要进一步修正。通过对多条M-H曲线的迭代求解得到非室温条件下的β值[13]。
将式(12)代入J-A模型,可仿真得到非室温条件下硅钢片的磁滞回线。图3a中为300K、400K、500K温度时的 B-H曲线,可见随着温度的升高,磁感应强度降低,图 3b中最大磁导率仿真结果与实测数据基本相符。
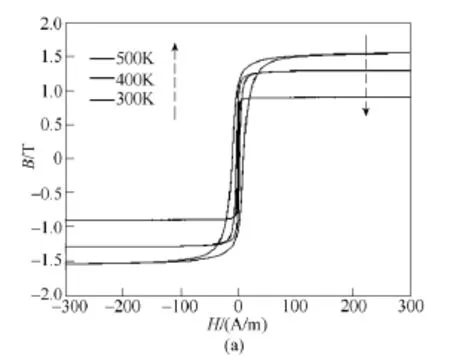
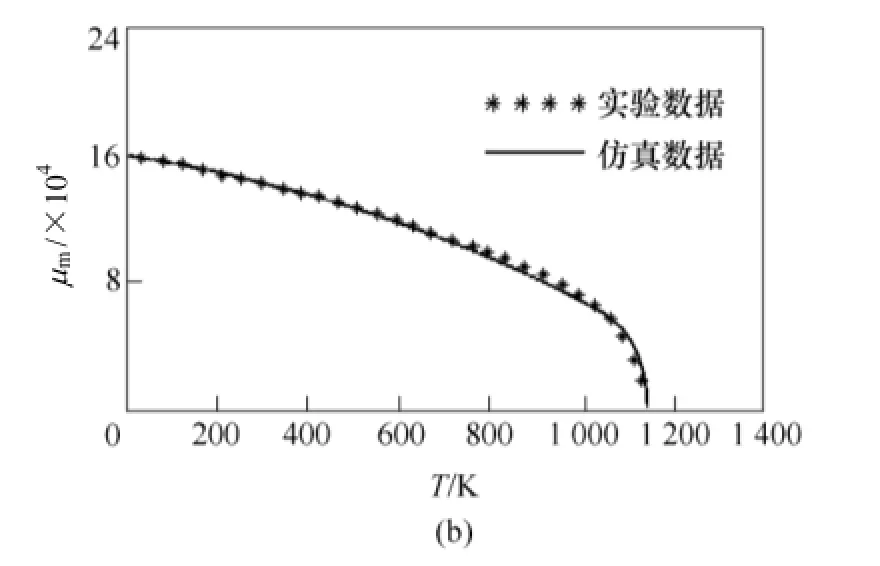
图3 不同温度下硅钢片B-H曲线Fig.3 Simulated B-H curve of Fe-Si magnetic sheet at different temperatures
(2)纳米晶和非晶合金温度特性较复杂,本文提出了分段修正方法。
1)当温度高于 Tc时,非晶合金发生晶化,磁性消失,饱和磁化强度计算式为
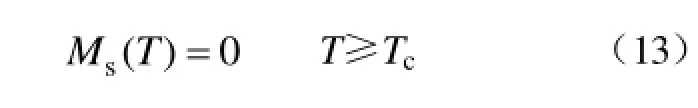
2)当温度高于Tb、低于Tc时,根据文献[14-15]的平均场理论,得到修正公式为
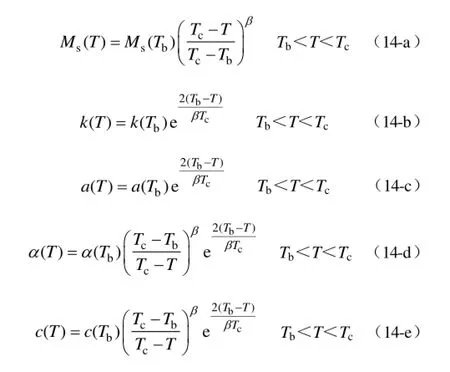
3)当温度低于 Tb时,根据多组数据提出拟合公式为
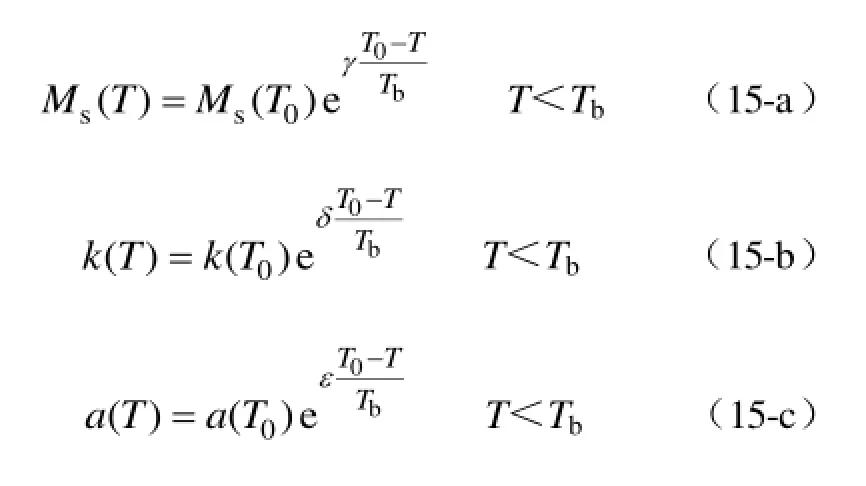
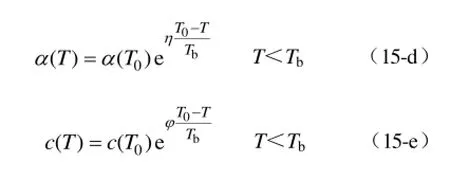
式中,φ、η、ε、δ、γ为修正系数。
与临界指数β的确定方法一样,修正系数可通过建立两个不同温度下的J-A模型、将参数代入式(15)得到初始修正系数,最后对多条M-H曲线通过迭代求解得到最佳修正系数。将修正式(13)~式(15)代入J-A模型得到不同温度下非晶合金与纳米晶材料的磁滞回线。仿真结果如图4所示,与图2中的实测数据相符。
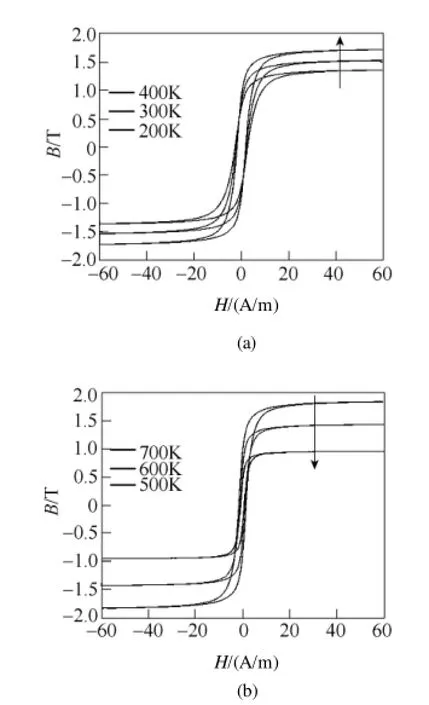
图4 不同温度下非晶合金B-H曲线Fig.4 Simulated B-H curve of amorphous alloys at different temperatures
建立磁滞回线数学模型后,可仿真得到不同温度下的磁化曲线,根据式(16)计算得到磁导率为
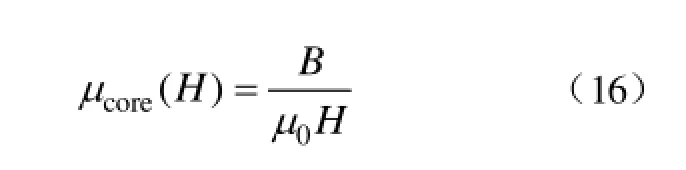
在图5中,以非晶合金为例计算得到不同温度下磁导率在磁场上升段的变化曲线。可见随磁场强度的增大,磁导率先增大后减小,且温度特性与图2、图4中的内容相符。
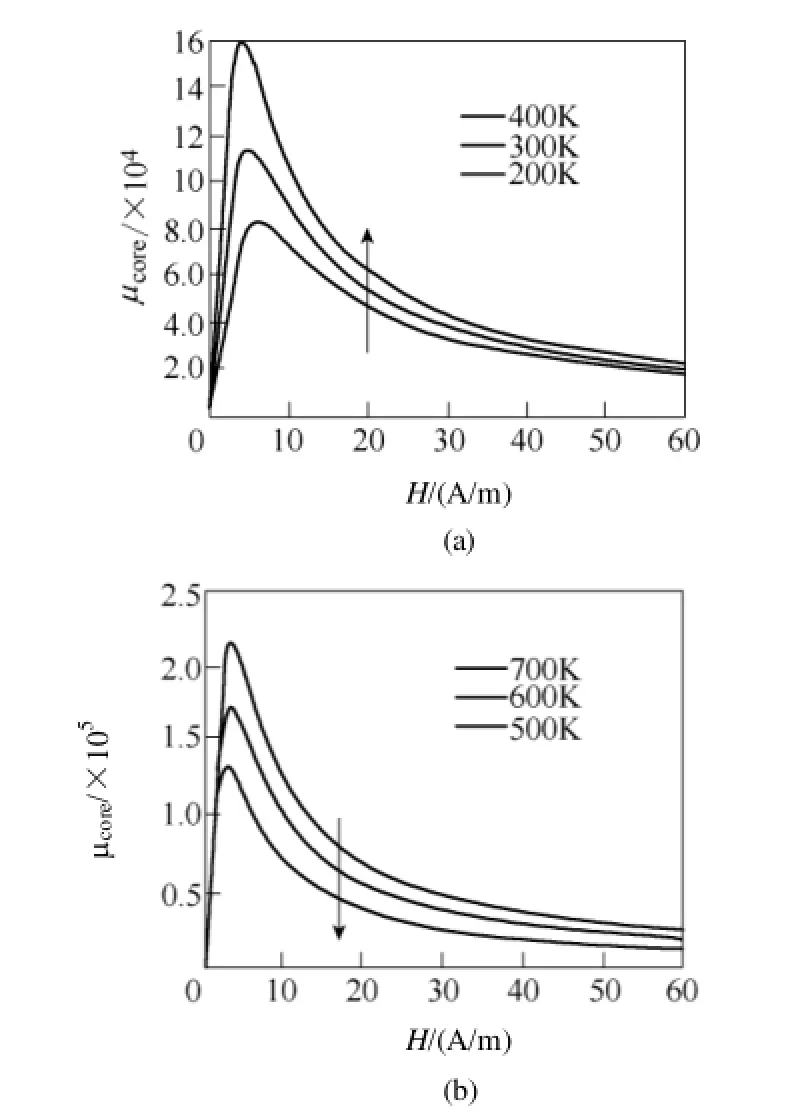
图5 磁导率随磁场强度、温度变化曲线Fig.5 Variation of magnetic permeability with magnetic field intensity and temperature
3.2 气隙温度特性分析
气隙长度受磁致伸缩效应的影响发生变化,而磁致伸缩系数随温度变化,加之热膨胀效应的影响,导致气隙长度在不同温度、不同磁场强度下变化。分析集磁式 OCS温度特性时,需要考虑磁致伸缩和热膨胀对气隙长度的影响。
文献[17-18]分别分析了硅钢片和非晶合金的磁致伸缩系数随磁场强度变化情况。如图6所示,磁致伸缩系数λ随磁场强度先增大后减小,当磁心饱和后,磁致伸缩系数基本稳定,记为饱和磁致伸缩系数λs。
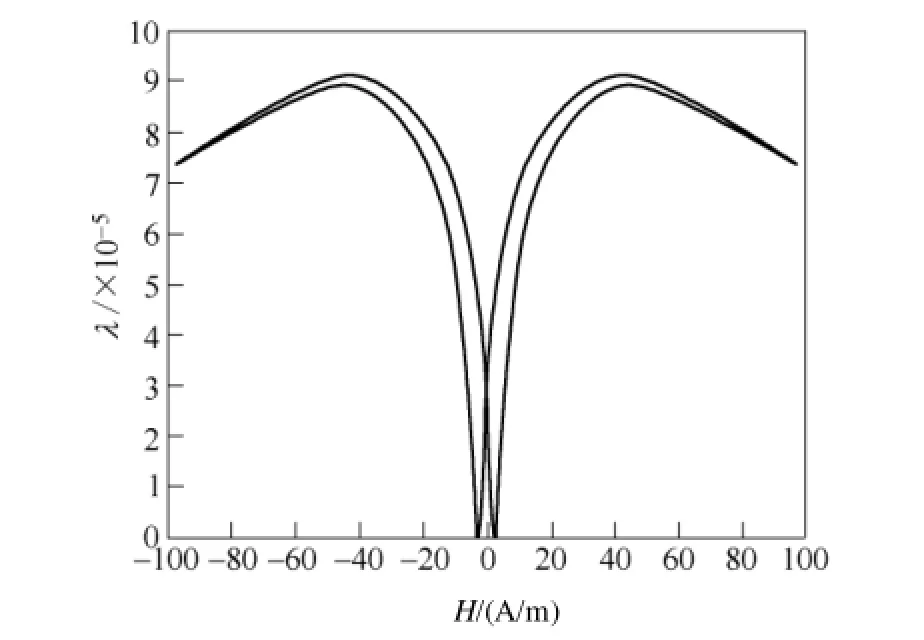
图6 磁致伸缩系数随磁场强度变化曲线Fig.6 Variation of magnetostriction coefficient with magnetic field intensity
根据文献[19-20]介绍的二次畴转模型,在磁滞回线非饱和段,得到磁致伸缩系数与磁化强度、饱和磁致伸缩系数之间的近似表达式为
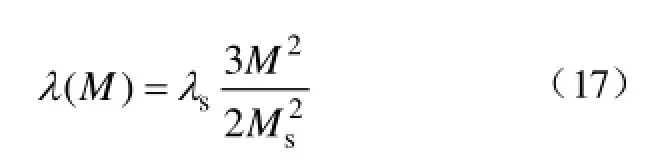
式中,M为磁化强度;Ms为饱和磁化强度。
文献[17]介绍了非晶合金饱和磁致伸缩系数的温度特性。如图 7所示,低于居里温度 Tc时,饱和磁致伸缩系数随温度上升而减小;大于 Tc后,温度继续上升使非晶合金发生晶化,导致饱和磁致伸缩系数先增大后减小,到达晶态居里温度 Txc后,饱和磁致伸缩系数减小至零。
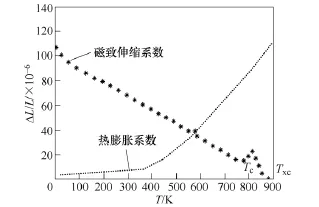
图7 热膨胀系数和磁致伸缩系数随温度变化曲线Fig.7 Variation of magnetostriction coefficient and thermal expand coefficient with temperature
引入温度参数,设磁致伸缩系数为 λs(T),根据实验数据近似拟合其表达式。以非晶合金为例,考虑电流传感器的环境温度范围,可以只对 Tb以下温度范围内的表达式进行拟合。饱和磁致伸缩系数为λs(T)的表达式拟合为
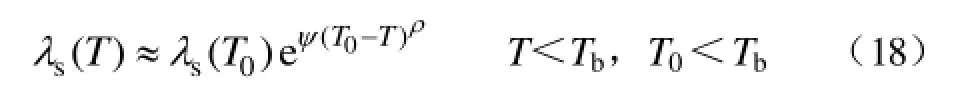
式中,λs(T0)为 T0温度下饱和磁致伸缩系数;ψ、ρ为修正系数。
式(18)与式(17)联立得
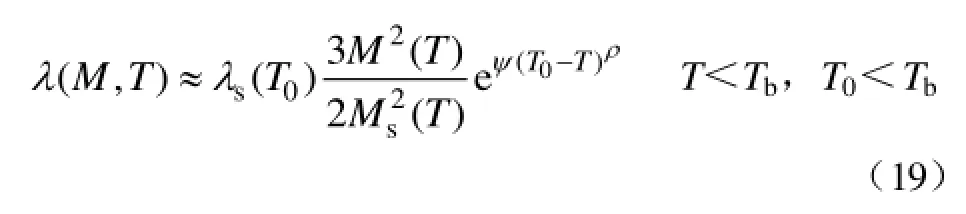
式中,M(T)、Ms(T)分别为温度 T下磁化强度、饱和磁化强度。
文献[21-22]介绍了非晶合金热膨胀系数的温度特性。由图7可见,在低于Tb的范围内,随着温度的上升热膨胀系数ξ(T)呈指数上升,ξ(T)表达式可拟合为
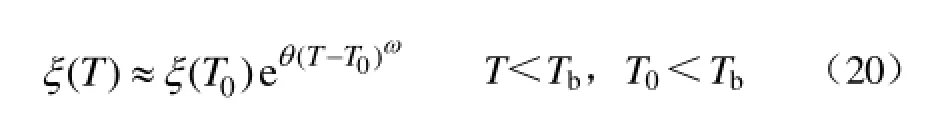
式中,ξ(T0)为 T0温度时的数据;θ、ω为修正系数。
同时考虑热膨胀与磁致伸缩时,磁心的磁路长度Lcore(M,T)为
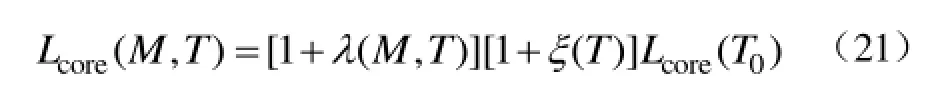
磁致伸缩和热膨胀引起的长度变化远大于体积变化,可认为磁心的平均周长L固定不变,因此气隙新长度为
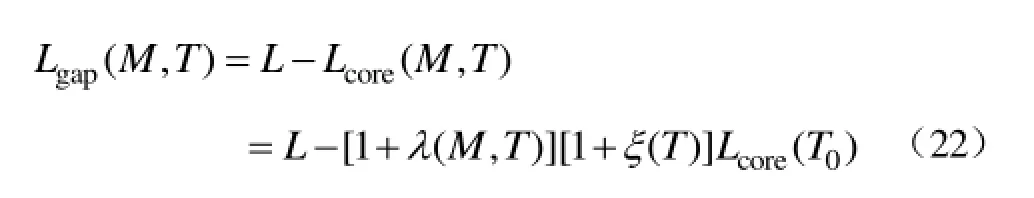
3.3 磁特性随温度变化的分析
前两节分别建立了磁导率和气隙长度随磁场强度和温度变化的数学模型。下面对集磁式OCS磁特性随温度变化进行分析。仿真步骤如下:
(1)首先确定基准温度T0下磁心的尺寸,然后通过物理性能测试仪 PPMS测量 Ms-T曲线和 M-H曲线,根据实验数据得到基准温度T0下J-A模型的参数和临界指数等修正系数,通过干涉测量仪测量基准温度T0下铁磁材料的磁致伸缩系数、热膨胀系数和温度修正系数。
(2)对铁磁材料建立带温度系数的J-A磁滞模型,仿真得到不同温度下的M-H曲线。根据磁化曲线计算得到不同磁场强度、温度下的磁导率为
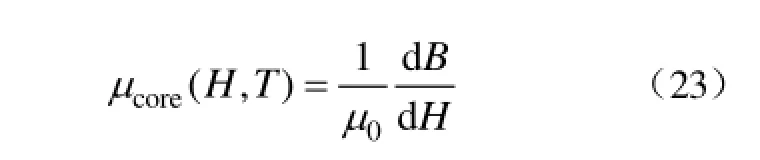
(3)根据M-H曲线,得到该磁场强度下的磁化强度 M,代入式(19)、式(20)得到磁致伸缩系数和热膨胀系数,然后代入式(22)得到气隙长度。
(4)根据磁导率和气隙长度,代入式(6)计算得到一次电流与磁感应强度的关系。
步骤(2)、(3)中均需要先确定磁心横截面上磁场强度 Hcore(T)的数值。对于集磁式 OCS,需要确定一次电流与磁心横截面上磁场强度之间的关系,根据式(3)和式(7)可知
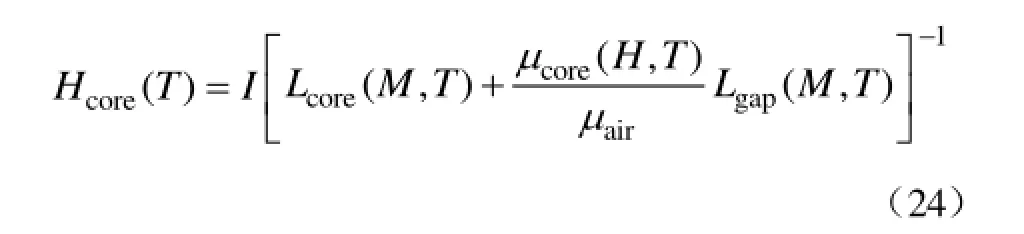
仿真流程如图8所示。根据软件流程仿真得到一次电流与磁心横截面上磁场强度、一次电流与磁感应强度的仿真曲线,结果如图9和图 10所示。
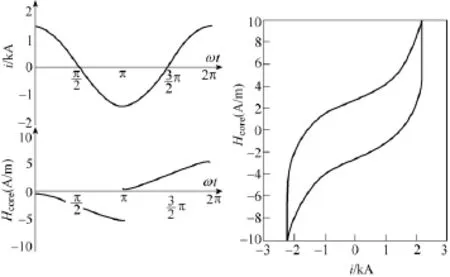
图9 一次电流-磁心横截面上磁场强度曲线Fig.9 Primary current and magnetic field intensity curve
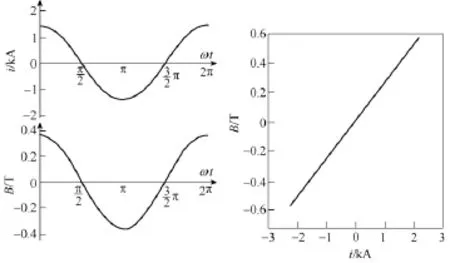
图10 一次电流-气隙处磁感应强度曲线Fig.10 Primary current and magnetic flux density curve
在仿真模型中代入不同的温度数值,可得到不同温度下气隙位置的磁感应强度,实现对集磁式OCS磁特性与温度特性的分析。以气隙长度为5mm、额定电流1kA的硅钢片集磁环为例建立仿真模型,仿真得到-15℃和 85℃时额定电流下气隙位置磁感应强度变化曲线,结果如图11a所示。可见不同温度下磁感应强度均呈正弦变化,但对其波谷与波峰进行放大可知,85℃时磁感应强度小于-15℃时数值,如图 11b、11c所示。
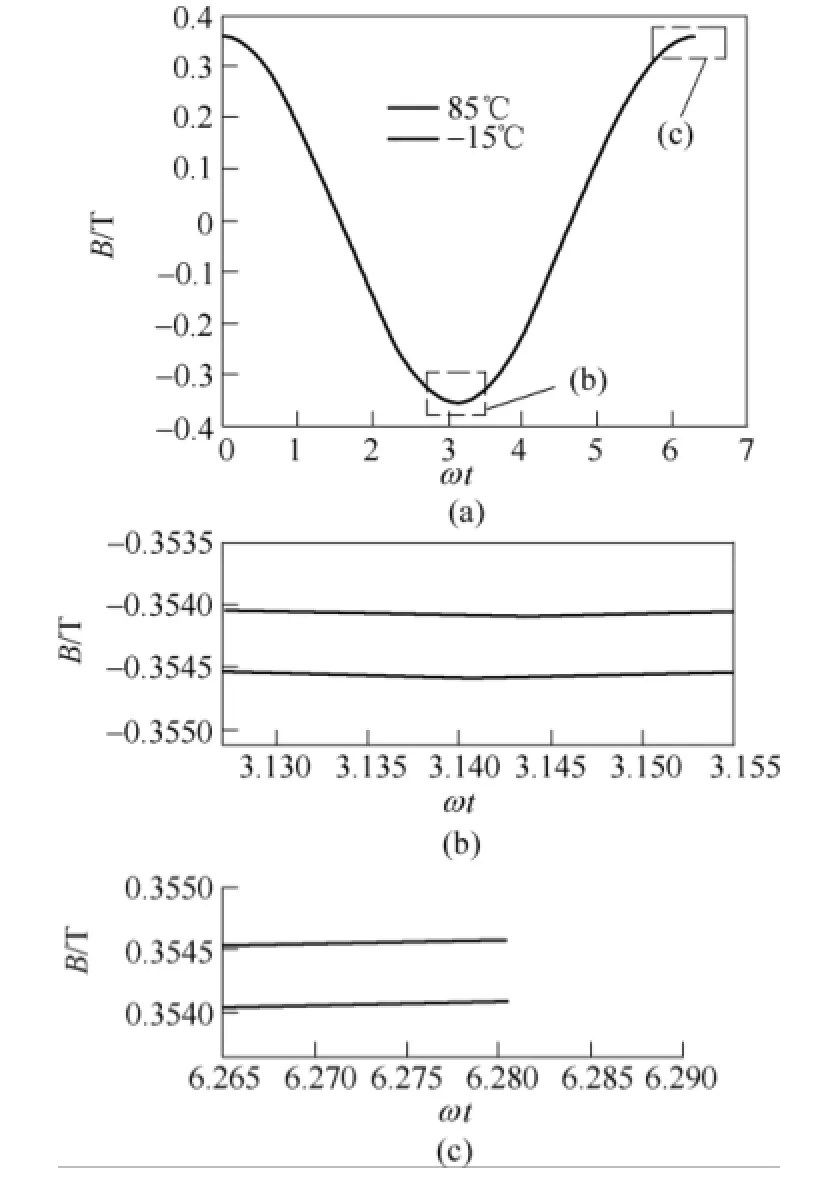
图11 不同温度下磁感应强度曲线Fig.11 Magnetic flux density curve at different temperatures
对图 11中的仿真结果进行分析知,85℃时测量得到磁感应强度值比-15℃时数值减小0.14%。可见集磁环的温度特性直接影响了集磁式 OCS的测量准确度。
3.4 一种具有稳定温度特性的传感头设计
由于硅钢片的磁导率随温度上升而减小,而磁致伸缩系数和热膨胀系数随温度的变化不大,总体上有约-0.14%的温度漂移,对 0.2级测量用电流互感器的影响不容忽视[23]。这种温漂是由磁性材料的固有特性决定的。本文结合非晶合金材料的温度特性,提出了一种具有稳定温度特性传感头设计方案:一方面,图2所示的非晶合金的磁导率在-40~85℃温度范围内随温度上升而增大;另一方面,图7所示随着温度的上升,热膨胀系数增大、磁致伸缩系数减小,但非晶合金磁致伸缩系数较大,热膨胀系数变化量远小于磁致伸缩系数的变化量,因此最终导致气隙长度增大。根据式(6)可知,当气隙长度增大时,磁场强度减小;磁导率增大时,磁场强度增大。两者对磁场强度作用相反,当两者变化程度基本一致时,集磁环将具有稳定的温度特性。而非晶合金磁导率、磁致伸缩系数随温度变化的程度,与合金配方、退火温度和退火时间等有关[22,24],因此通过选取合适的非晶材料,在-40~85℃温度范围内,气隙处磁感应强度将基本不随温度变化。
本文选取一种铁基非晶合金并建立仿真模型,得到一次电流-磁感应强度曲线如图 12所示。在一次电流上升段,磁感应强度随温度上升而增大;在一次电流下降段,磁感应强度随温度上升而减小;计算知,85℃时一周期内磁感应强度的有效值比-15℃时数值增大 0.02%,远小于硅钢片集磁环0.14%的变化,可见选取的铁基非晶合金集磁环具有稳定温度特性。
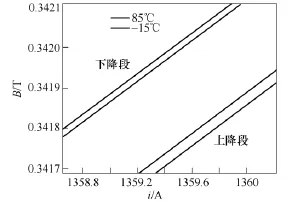
图12 非晶合金的一次电流-气隙处磁感应强度曲线Fig.12 Primary current and magnetic flux density curve of amorphous alloys
4 实验验证
本文对铁基非晶合金材料的集磁环在温度范围-40~85℃、额定电流 1kA时的磁特性进行了实验验证。采用的磁心基本结构如图 13所示。

图13 铁基非晶合金磁心结构图Fig.13 Geometric structure of Fe-based amorphous cores
首先通过闭合磁心对J-A模型的温度修正公式进行实验验证。将闭合磁心放置在温度箱内,通过示波器法测量不同温度下的 B-H曲线。图 14是采用示波器法测量闭合磁心B-H曲线的实验波形。根据不同温度下的B-H曲线和非晶合金材料手册确定磁滞模型参数见表1和表 2。
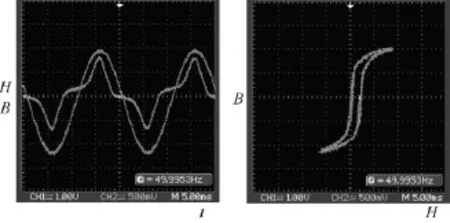
图14 磁滞回线实验波形Fig.14 Measured hysteresis loops
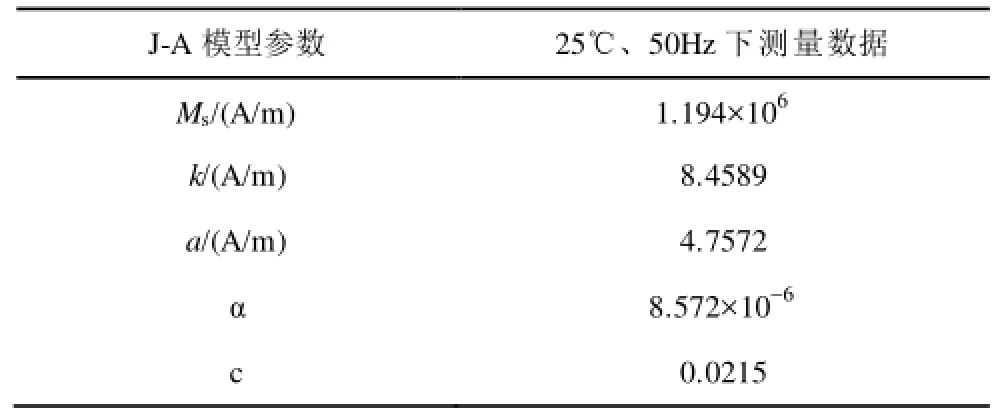
表1 铁基非晶合金J-A模型参数Tab.1 J-A model parameters for a Fe-based amorphous core
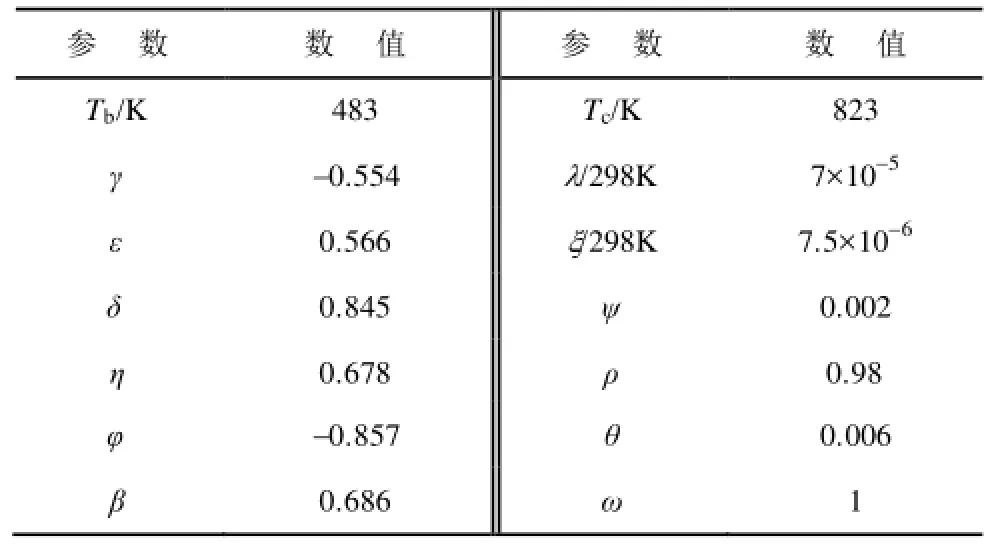
表2 其他参数Tab.2 Other parameters
仿真与实验对比波形如图 15所示。可见,在-40~85℃的温度范围内(小于Tb),随着温度的上升,最大磁化强度增大,矫顽力减小,磁导率增加。仿真与实验波形基本一致,表明了J-A模型及温度修正公式的有效性。
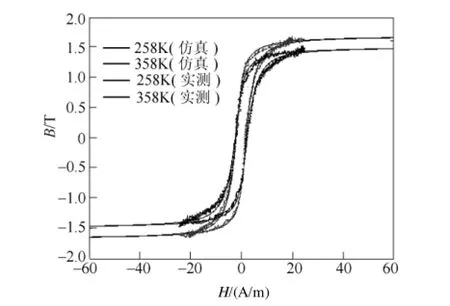
图15 仿真与实验波形Fig.15 Simulated and measured hysteresis loops
接下来对集磁环温度特性进行实验验证。由式(5)得知,可根据气隙处磁感应强度来确定气隙磁场强度,因此实验直接测量的是气隙磁感应强度。此外,光学器件也受温度的影响,为了获得集磁环准确的温度特性,在此移除了集磁式 OCS中磁光材料等光学器件,直接测量气隙处的磁感应强度。具体实验方案如下:一次导线穿过通过集磁式 OCS的集磁环,集磁环放置于高低温交变湿热试验箱SDJ402内,将高斯计探头放置在气隙位置;磁感应强度通过高斯计、一次电流通过泰克电流探头 A621将信号分别接入示波器。一次导线通过 1kA额定电流时,电流探头变比设置为 1kA/1V、高斯计探头变比为1T/1V,得到实验波形如图16所示,可见磁感应强度呈正弦变化,与一次电流成正比。
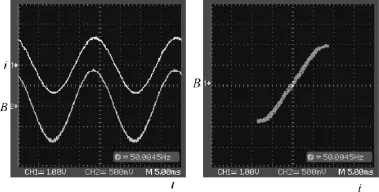
图16 一次电流与磁感应强度实验波形Fig.16 Simulated and measured hysteresis loops
此外气隙长度较小时,磁感应强度随温度变化量较大,由于采用的高斯计精度为 0.1mT,为获得较准确的实验结果,集磁环气隙长度值不宜过大,在此选取5mm。由于气隙磁场强度有效值随温度变化率低于0.2%,无法通过示波器直接肉眼观测,在此将数据存储后进行变化率的计算。以25℃时测量值为基准,得到-40~85℃温度下气隙磁场强度的变化率,如图17所示。随着温度上升,硅钢片集磁环气隙磁场强度变化率由正值变为负值,证明气隙磁场强度值减小,与仿真结果一致;而非晶合金集磁环气隙磁场强度变化率在 0.02%以内,基本具有稳定的温度特性。因此,集磁环气隙处磁感应强度的测量结果验证了仿真模型的有效性。
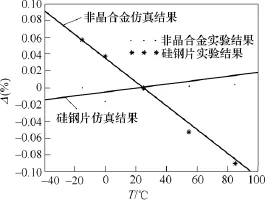
图17 不同温度下测量结果变化率Fig.17 Change rate of measurement results at different temperatures
5 结论
(1)建立了铁磁材料带温度系数的磁滞模型。根据铁磁材料温度特性的区别,将其分为两类并在J-A模型基础上提出修正公式,弥补了 J-A模型无法反应温度特性的缺陷。
(2)通过提出磁致伸缩系数、热膨胀系数的温度修正公式,修正了集磁环气隙长度值。
(3)对集磁式OCS建立了带温度参数和气隙参数的磁场模型。实现了集磁环磁特性随温度变化的分析。
(4)提出了一种具有稳定温度特性的集磁式OCS传感头设计方法。非晶合金材料磁导率与气隙长度随温度变化对气隙处磁场强度的影响作用相反,通过选取合适非晶材料,可使气隙处磁感应强度在一定的温度范围内基本保持不变。通过对一种铁基非晶合金集磁环的实验验证,证明了设计方案的可行性。
(5)本文提供的材料参数和建模方法具有实用价值,可用于传感器、变压器等磁特性与温度特性的耦合仿真研究、磁性材料选择等场合。
[1] 于文斌, 张国庆, 路忠峰, 等. 光学电流互感器的抗干扰分析[J]. 电力系统保护与控制, 2012, 40(12): 8-12.
Yu Wenbin, Zhang Guoqing, Lu Zhongfeng, et al. Analysis of resistance disturbance capability of optical current transformers[J]. Power System Protection and Control, 2012, 40(12): 8-12.
[2] 陈金玲, 李红斌, 刘延冰, 等. 一种提高光学电流互感器温度稳定性的新方法[J]. 电工技术学报,2009, 24(4): 97-101.
Chen Jinling, Li Hongbin, Liu Yanbing, et al. A novel method to improve the temperature stability of optical current transformer[J]. Transactions of China Electrotechnical Society, 2009, 24(4): 97-101.
[3] 张朝阳, 张春熹, 王夏霄, 等. 光纤电流互感器λ/4波片温度误差补偿[J]. 电工技术学报, 2008, 23(12): 55-59.
Zhang Chaoyang, Zhang Chunxi, Wang Xiaxiao, et al. Temperature compensation methods of λ/4 wave plate for fiber optic current sensor[J]. Transactions of China Electrotechnical Society, 2008, 23(12): 55-59.
[4] 李红斌, 刘延冰. 光学电流互感器温度补偿方法[J].仪表技术与传感器, 2004(4): 32-39.
Li Hongbin, Liu Yanbing. Temperature compensatory methods of optical current transformer[J]. Instrument technique and sensor, 2004(4): 32-39.
[5] 李红斌, 汪本进, 刘延冰. 光学电流互感器二次部分温度特性及其改善[J]. 电测与仪表, 2004, 41(1): 13-16.
Li Hongbin, Wang Benjin, Liu Yanbing. Study on temperature performance and improvement method of secondary part of optical current transformer[J]. Electrical Measurement & Instrumentation, 2004, 41(1): 13-16.
[6] 王佳颖, 郭志忠, 李洪波, 等. 集磁环式光学电流互感器的结构优化[J]. 电力自动化设备, 2011, 31(9): 23-26.
Wang Jiaying, Guo Zhizhong, Li Hongbo, et al. Structure optimization of optical current transformer with magnetic concentrator ring[J]. Electric Power Automation Equipment, 2011, 31(9): 23-26.
[7] Jia Xiao, Chen Dairon, Jiao Xiulin, et al. Monodispersed Co, Ni-Ferrite nanoparticles with tunable sizes: controlled synthesis, magnetic properties, and surface modification[J]. Journal of Chemical Physics C, 2008, 112(4): 911-917.
[8] Jongnam Park, Eunwoong Lee, Nong-Moon Hwang, et al. One-nanometer-scale size-controlled synthesis of monodisperse magnetic iron oxide nanoparticles[J]. Angewandte Chemie International Edition, 2005, 19(44): 2872-2877.
[9] 李贞, 李庆民, 李长云, 等. J-A 磁化建模理论的质疑与修正方法研究[J]. 中国电机工程学报, 2011, 31(3): 124-131.
Li Zhen, Li Qingmin, Li Changyun, et al. Queries on the J-A modelling theory of the magnetization process in ferromagnets and proposed correction method[J]. Proceedings of the CSEE, 2011, 31(3): 124-131.
[10] Garikepati P, Chang T T, Jiles D C. Theory of ferromagnetic hysteresis: evaluation of stress from hysteresis curves[J]. IEEE Transactions on Magnetics, 1988, 24(6): 2922-2924.
[11] Jiles David C, Atherton David L. Theory of ferromagnetic hysteresis[J]. Journal of Applied Physics, 1984, 55(6): 2115-2120.
[12] Jiles D C. Frequency dependence of hysteresis curves in conducting magnetic materials[J]. Journal of Applied Physics, 1994, 76(10): 5849-5855.
[13] 李晓萍, 彭青顺, 李金保, 等. 变压器铁心磁滞模型参数辨识[J]. 电网技术, 2012, 36(2): 200-205.
Li Xiaoping, Peng Qingshun, Li Jinbao, et al. Parameter identification of hysteresis loop model for transformer core[J]. Power System Technology, 2012, 36(2): 200-205.
[14] Raghunathan A, Melikhov Y, Snyder J E, et al. Theoretical model of temperature dependence of hysteresis based on mean field theory[J]. IEEE Transactions on Magnetics, 2010, 46(6): 1507-1510.
[15] Anthony Arrott, John E Noakes. Approximate equation of state for nickel near its critical temperature[J]. Physical Review Letters, 1967, 19(14): 786-789.
[16] 纪松, 钱坤明, 谭锁奎, 等. 基于Hopkinson效应的计算机控制软磁材料居里温度测量仪的研制[J]. 磁性材料及器件, 2005, 36(4): 34-37.
Ji Song, Qian Kunming, Tan Suokui, et al. Development of computer aided curie temperature metrical instrument for soft magnetic materials applying hopkinson effect[J]. Journal of Magnetic Materials and Devices, 2005, 36(4): 34-37.
[17] 何正明, 赵妙余, 张玲芬, 等. 铁基非晶合金磁致伸缩的温度效应[J]. 物理学报, 1990, 39(4): 656-660.
He Zhengming, Zhao Miaoyu, Zhang Lingfen, et al. Effects of temperature on saturation magnetostriction in iron-rich amorphous alloys[J]. Acta Physica Sinica, 1990, 39(4): 656-660.
[18] 冯大军, 朱业超, 黄璞, 等. 无取向硅钢片磁致伸缩特性的实验研究[J]. 武汉工程职业技术学院学报,2009, 21(3): 13-15.
Feng Dajun, Zhu Yechao, Huang Pu, et al. Laboratorial study on magnetostriction characteristics of non-oriented silicon steel sheet[J]. Journal of Wuhan Engineering Institute, 2009, 21(3): 13-15.
[19] 曹淑瑛, 王博文, 闫荣格, 等. 超磁致伸缩致动器的磁滞非线性动态模型[J]. 中国电机工程学报, 2003, 23(11): 145-149.
Cao Shuying, Wang Bowen, Yan Rongge, et al. Dynamic model with hysteretic nonlinearity for a giant magnetostrictive actuator[J]. Proceedings of CSEE, 2003, 23(11): 145-149.
[20] Calkins F T, Smith R C, Flatau A B. Energy-based hysteresis model for magnetostrictive transducers[J]. IEEE Transactions on Magnetics, 2000, 36(2): 429-439.
[21] 肖红文, 刘蕴韬, 卢志超, 等. 非晶材料的热膨胀系数和声子谱测量与纳米晶成形机制的关联[J]. 原子能科学技术, 2010, 44(增刊): 43-47.
Xiao Hongwen, Liu Yuntao, Lu Zhichao, et al. Formation mechanism of nanocrystalline related to thermal expand coefficient and generalized phonon spectra in amorphous[J]. Atomic Energy Science and Technology, 2010, 44(Supplyment): 43-47.
[22] 卢志超, 鲜于泽, 沈保根, 等. Fe基非晶和纳米晶合金的热膨胀[J]. 材料研究学报, 1995, 9(1): 13-15.
Lu Zhichao, Xian Yuze, Shen Baogen, et al. Thermal expansion properties of Fe-based amorphous and nanocrystalline alloys[J]. Chinese Journal of Materials Research, 1995, 9(1): 13-15.
[23] GB/T 20840.8, 互感器-第8部分: 电子式电流互感器[S].
[24] 黄军庆, 傅明喜, 王斌, 等. 退火温度对非晶合金Fe69Al5Ga2P9.65B4.6Si3C6.75磁性能的影响[J]. 特种铸造及有色合金, 2011, 31(12): 1142-1144.
Huang Junqing, Fu Mingxi, Wang Bin, et al. Effects of annealing temperature on magnetic properties of Fe69Al5Ga2P9.65B4.6Si3C6.75amorphous alloys[J]. Special Casting & Nonferrous Alloys, 2011, 31(12): 1142-1144.
Research on the Temperature Dependence of the Magnetic Properties of Optical Current Sensor with Magnetic Concentrator
Li Chao Wang Xiajing Xu Qifeng
(College of Electrical Engineering and Automation Fuzhou University Fuzhou 350108 China)
Temperature-drift limits the application of optical current sensor(OCS), study is now focused on the analysis of the temperature characteristics of optical devices and there is no enough research on the variation of magnetic properties with temperature. Magnetic permeability and air gap length are changed with temperature, it is necessary to analyze the magnetic properties coupled temperature. The magnetic model including thermal effects and air gap factors are proposed by incorporating the temperature into the original Jiles-Atherton model and adding magnetostriction coefficient and thermal expand coefficient to correct the length of air gap. A new design of air gapped amorphous core with stable temperature characteristics is proposed based on the new model. The experiments on a Fe-based amorphous core are conducted and the results show good agreement between the simulation and the experiment.
Optical current sensor, temperature, Jiles-Atherton model, hysteresis loop, magnetic concentrator, ferromagnetic material, air gap
TM152
李 超 男,1983年生,博士研究生,工程师,研究方向为电力电子技术在电力系统中的应用。
国家自然科学基金项目(51177016)和国家电网公司科技项目(闽电发展[2012]88)资助项目。
2013-12-10 改稿日期 2013-12-10
王夏菁 女,1989年生,硕士研究生,研究方向为光学电流传感器相关技术。

