11 辊矫直机矫直过程中性层偏移量分析

李长乐，桂海莲，李 曜

(太原科技大学材料学院，山西 太原 030024;太原科技大学机械学院，山西 太原 030024)

0 前言

《2011～2020 年中国钢铁工业科学与技术发展指南》［1］中将“新一代可循环钢铁流程工艺与装备技术”和“新一代控轧控冷技术”作为钢铁行业“十二五”期间重点优化、完善和推广的关键技术，对钢板的工艺流程和装备技术提出更高要求。《指南》指出“关于智能化钢铁生产的各项技术研发、推广优化的问题已十分迫切地摆在我们面前。这是现代化钢厂实施以计算机全自动、高精度控制钢铁生产全过程工艺与装备，实现生产效率最高、物耗能耗最低、生产成本最小、产品质量最佳、排放趋零总体目标的必要条件。”做为提高钢板产品质量的矫直设备，更应该从基础理论对矫直过程进行研究，建立合理的矫直力模型，以适应生产的需要，为高精度、高效率生产提供必要的技术支持。

辊式矫直机矫直过程的研究一般采用解析法或数值分析法，并且近年来数值分析方法应用更加广泛。崔甫［2］是我国较早研究矫直理论与计算的学者，他曾系统的分析了影响矫直力的众多参数。杨晓君［3］利用Marc 对十一辊矫直过程进行有限元模拟并分析了截面上各种应力应变的分布规律。周晓宇［4］确定了中厚板辊矫中压弯量、弯辊凸度等参数，并利用VB 语言编写中厚板冷矫直工艺计算软件。张卫红［5］在传统力能参数模型的基础上，对11 辊板带矫直机进行分析研究，提出了一种基于虚拟支点和曲线拟合的新力能参数计算模型。东北大学薛军安［6］研究了辊式矫直过程中接触倾角与曲率的变化规律，说明接触倾角具有累计效应。武汉科技大学杨云［7］研究了七辊矫直机矫直力计算模型，太原科技大学周存龙［8，9］利用面积－力矩第二定律，建立了弯矩与挠度的关系式，确定了辊式矫直过程中板带的弯曲挠度。太原科技大学王效岗［10，11］对十五辊组合矫直机的关键技术进行了系统研究。本文重点研究中性层偏移在矫直过程中的作用，确定中性层偏移计算公式，结合数值分析拟合中性层偏移变化曲线，为矫直力模型的精确确定提供理论依据。

1 理论分析中性层偏移量

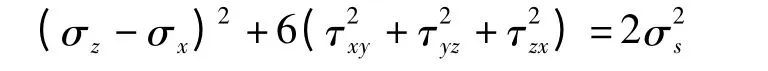
对于平面应变问题可简化为

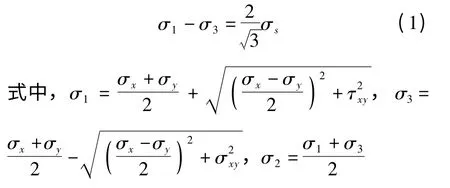
在传统矫直理论中，认为矫直件在矫直过程中几何中心层与应力中性层是重合的，如图1a所示，在整个矫直过程中应力中性层不会发生偏移。在某些特定的情况下，中性层偏移量相对于矫直件厚度是不可忽略的，它的偏移形式如图1b 所示。在图1a 中，应力中性层处于板厚中心位置，上下拉伸区和压缩区的弹性变形区相等，上下表面的应力值σx=σx';但在图1b 中，由于应力中性层向下发生了偏移，所以以几何中心层为界产生的弹性区厚度不同，并且上下表面的应力值也不同。

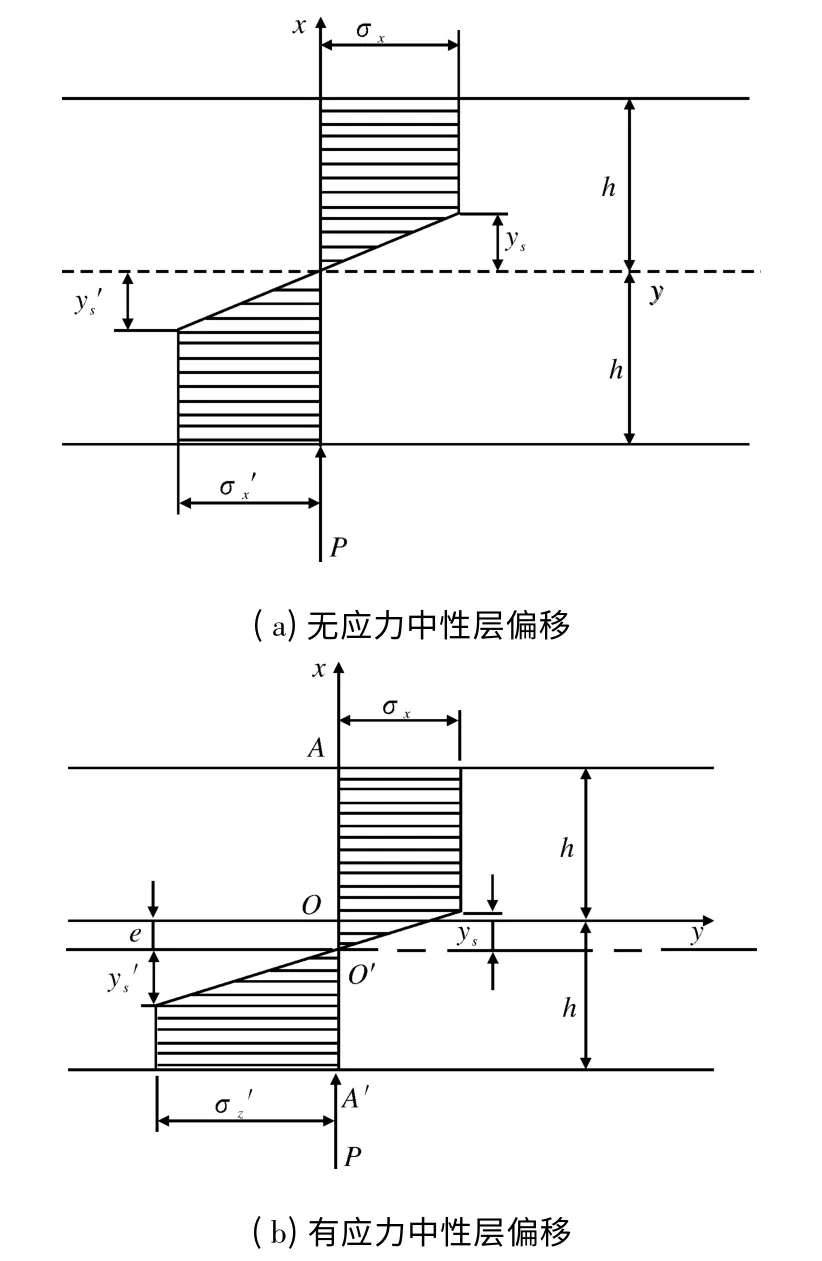
图1 理想材料弹塑性弯曲应力图Fig.1 Plastic bending of perfect material

假设中性层向下发生偏移，偏移量为e，如果e ＞0，则说明应力中性层向下发生了偏移;如何e ＜0，则说明应力中性层向上发生了偏移;如何e=0，则说明应力中性层没有发生偏移。根据上述分析，由∑Px=0 得

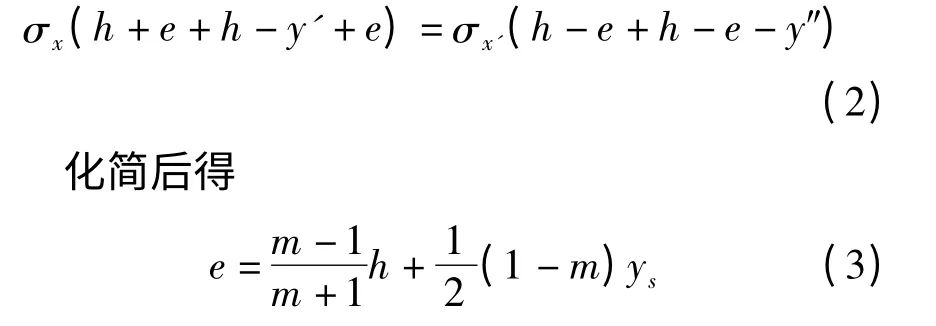
不考虑中性层偏移的力矩公式［12］为

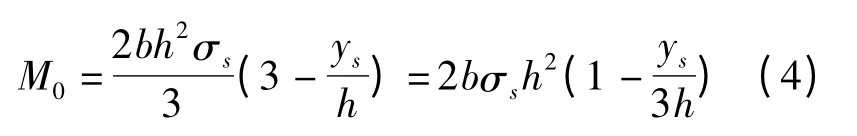
考虑中性层偏移的力矩公式为:

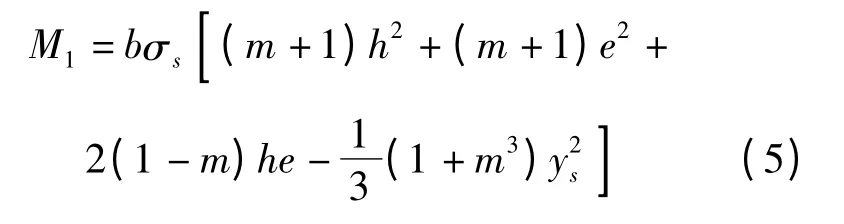
2 数值分析计算

计算模型来源于本实验室的11 辊全液压矫直机实验平台，如图2 所示。在ansys 有限元分析软件中建立模型，如图3 所示。模型为轧辊半径0.06 m，板尺寸为:1.2 m ×0.08 m ×0.6 m(长×厚×宽)，板的相对原始曲率为5.18。

图2 全液压矫直机实验平台Fig.2 11 rollers plate leveler

图3 计算模型Fig.3 The calculation model

取一个矫直单元，如图4 所示。对施加不同力后矫直件横截面的弹塑性变形进行研究分析，观察几何中心层上下拉伸区和压缩区的塑性变形规律，进而研究中心层偏移的变化。

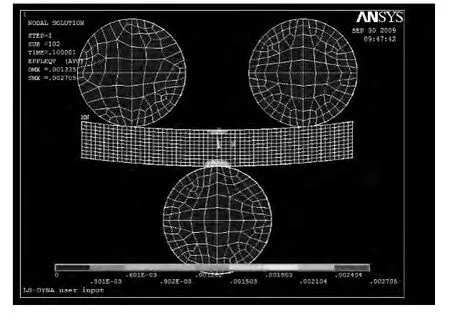
图4 一个矫直单元Fig.4 A straightening unit

2.1 受力2 MN

从图5 中可知拉伸区和压缩区均发生了塑性变形，但二者的变形程度有所不同。经过测量得知:中性轴左侧上半部分的弹性区为31.5 mm，下半部分的弹性区为26.9 mm，所以中性层向上偏移约为2.3 mm，中性轴上半部分的弹性区为30.3 mm，下半部分的弹性区为30.1 mm，所以中性层向上偏移约为0.1 mm，中心轴右侧上半部分的弹性区为31.3 mm，下半部分的弹性区为27.2 mm，所以中性层向上偏移约为2.05 mm。这说明塑性变形最大的区域不再中性轴处，而是在其左右两侧。从测量数据可以看出中性层偏移最大的是发生在中性轴两侧，并非是中性轴上。

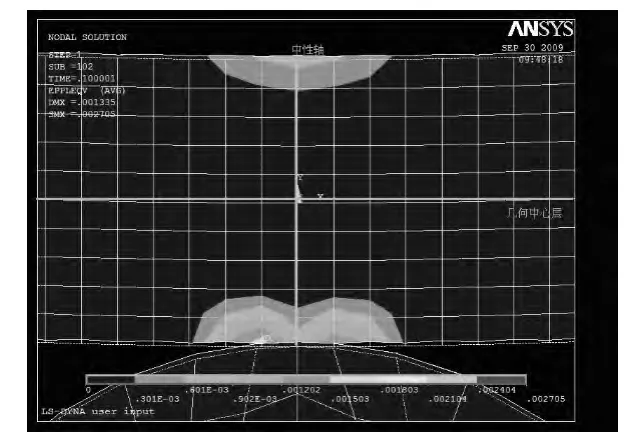
图5 局部细化图Fig.5 Local thinning image

利用公式(3)、(4)和(5)计算得到的中性层偏移量和弯矩的值为:

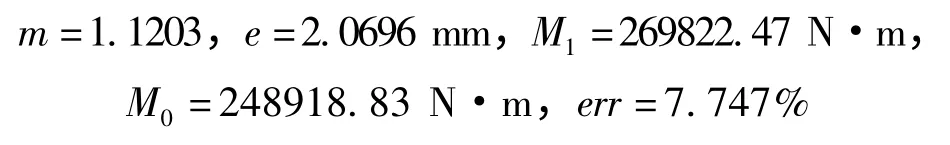
2.2 受力2.5 MN

图6 和图4 比较可知，随着受力的增大，塑性区也在不断增大。从图7 中测量得到中性轴左侧上半部分的弹性区为24.2 mm，下半部分的弹性区为24 mm，所以中性层向上偏移约为0.1 mm，中性轴上半部分的弹性区为24.1 mm，下半部分的弹性区为26.3 mm，所以中性层向下偏移约为1.1 mm，中心轴右侧上半部分的弹性区为24.2 mm，下半部分的弹性区为24 mm，所以中性层向上偏移约为0.1 mm。

利用上一部分推导的中性层偏移量计算公式得到的中性层偏移量的值为:

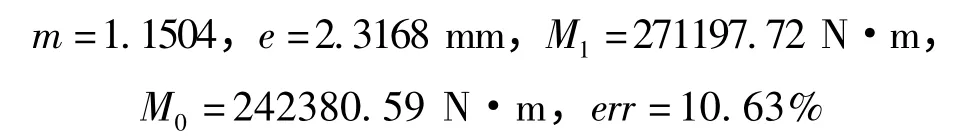
利用上述计算结果，对中性层偏移量进行数据拟合，拟合曲线如图8 所示。

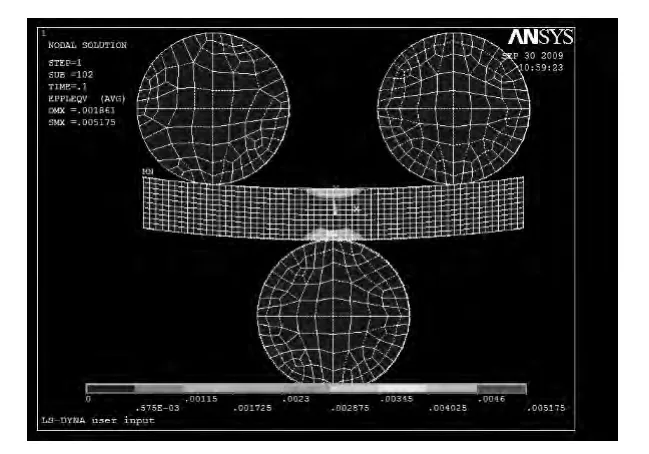
图6 一个矫直单元Fig.6 A straightening unit

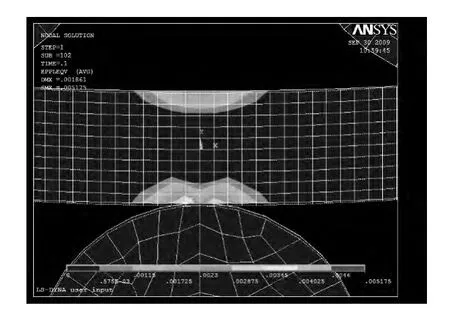
图7 局部细化图Fig.7 Local thinning image

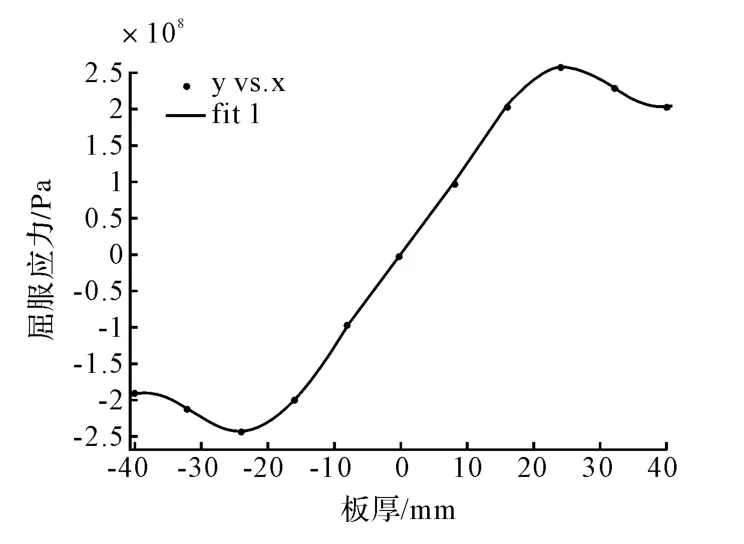
图8 数据拟合曲线Fig.8 Fitting curve

3 结论

本文首先通过力学推导，得到中性层偏移的计算公式，并推导出考虑中性层偏移时的弯矩力矩计算公式。通过有限元分析和测量，说明在中厚板辊式矫直过程中，中性层偏移是存在的，并且将测量值与理论计算值进行了对比，是否考虑中性层偏移导致的力矩的误差在10%左右。这说明中性层偏移量对矫直力的精确确定具有一定的影响，所以在矫直力模型的建立中应当考虑中性层偏移这个影响因素。

［1］中国金属学会，中国钢铁工业协会编.2011～2020年中国钢铁工业科学与技术发展指南［C］.北京:冶金工业出版社，2012.

［2］崔甫.矫直原理与矫直机械(第2 版)［M］.北京:冶金工业出版社，2007

［3］杨晓君.中厚板辊式矫直过程算法模型修正［D］.太原:太原科技大学，2011.

［4］周晓宇.中厚板冷矫直工艺参数研究及数学模型优化［D］.太原:太原科技大学，2011.

［5］张红卫.基于虚拟支点与曲线拟合的板带矫直机力能参数模型研究［D］.武汉:武汉科技大学，2011.

［6］薛军安，崔丽，胡贤磊，等.辊式矫直过程的接触倾角与曲率耦合分析［J］.中国冶金，2009，19(2):23－26.

［7］杨云，李友荣，王志刚.七辊板带矫直机矫直力计算模型研究［J］.冶金设备，2009(2):55－57.

［8］周存龙，王国栋，谢东钢，等.辊式矫直过程中板带弯曲挠度的确定［J］.太原科技大学学报，2009，30(1):48－50.

［9］周存龙，王国栋，刘相华.压弯量对轧件矫直变形影响的有限元分析［J］.塑性工程学报，2006，13(1):78－81.

［10］王效岗，黄庆学，马勤.中厚板的横向波浪矫直研究［J］.中国机械工程，2009，20(1):95－98.

［11］王效岗.十五辊组合矫直机关键技术及理论模型的研究［D］.兰州:兰州理工大学，2008.

［12］黄庆学.轧钢机械设计［M］.北京:冶金工业出版社，2007.

［13］Hai-Lian Gui，Qiang Li，Qing-Xue Huang.Analysis of rolled piece deformation in straightening process using FM-BEM［J］.Journal of marine science and technology，2014，22(5):550－556.