限电弃风工况下双馈风电机组有功及调频控制策略

米增强 刘力卿 余 洋 杜 平 袁 贺

(1.华北电力大学新能源电力系统国家重点实验室 保定 0710032.国网内蒙古东部电力有限公司调度控制中心 呼和浩特 010020)



限电弃风工况下双馈风电机组有功及调频控制策略

米增强1刘力卿1余 洋1杜 平2袁 贺1

(1.华北电力大学新能源电力系统国家重点实验室 保定 0710032.国网内蒙古东部电力有限公司调度控制中心 呼和浩特 010020)

双馈风电机组限电弃风运行能够为电网提供备用和频率支撑。为减小限电弃风工况下转速和桨距角频繁动作致使机组产生的机械疲劳，提出一种基于机组运行点转移轨迹优化的有功控制策略，并通过引入下垂控制使其具备了参与电网一次调频的功能。对限电弃风工况下机组在不同运行点处的稳定性进行分析；考虑机组有功平衡及运行点稳定性等约束条件，建立以转速和桨距角综合调整量最小为目标函数的运行点转移轨迹优化模型，并提出优化模型在出现不可行解时的处理机制，以获得可行的最优转移轨迹；建立机组运行轨迹和调频控制器，并对变桨系统和转子侧变频器的传统控制策略进行改进，使机组能够沿最优转移轨迹调整有功和参与调频。仿真结果表明，利用所提控制策略能使机组在准确完成限电弃风任务并为电网提供频率支撑的同时，大大减少机组转速和桨距角的调整量。

双馈风电机组 限电弃风 一次调频 综合调整量 转移轨迹优化

0 引言

据全球风能理事会(GWEC)统计，截止2013年底，世界新增风电装机容量35 289 MW，总装机容量达到318 105 MW[1]。由于风电单方面快速发展，而电网建设相对滞后，大规模风电并网给电网功率平衡和安全经济运行带来的挑战日益严峻，为此各国纷纷修改风电场并网准则，对风电场提出了更加严格的要求。2011年12月30日，我国颁布了国家标准GB/T 19963—2011《风电场接入电力系统技术规定》，明确提出风电场必须具备有功功率调节能力和参与电力系统调频和备用的能力[2]。德国E.ON Netz电网公司规定装机容量大于100 MW的风电场必须具备参与电力系统调频的能力，且调频容量不小于装机容量的±2%[3]。由丹麦、芬兰、挪威和瑞典共同发布的北欧风电场并网准则也明确提出风电场必须具备有功功率调节和响应系统频率变化的能力[4]。

为确保系统安全经济运行，风电场在一些时段接受电网调度部门命令运行于限电弃风工况已成为常态[5，6]。风电场限电弃风运行无疑会产生损失和浪费，但风电场通过适当弃风也就具备了类似于传统发电中功率热备用的能力，为风电场参与电网调频创造了条件，对维持系统的安全经济运行和推动风电持续发展具有重要意义[7-9]。因此，有必要对限电弃风工况下风电机组的有功及调频控制策略进行深入研究。

双馈风电机组(Doubly Fed Induction Gener-ator Wind Turbines，DFIG)是目前应用最广泛的机组类型，国内外对其有功功率控制策略进行了大量研究。文献[10，11]通过增加DFIG的转速使其偏离最优值，实现降出力运行。但受机组转速最大值限制，该控制策略只能在低风速工况下应用，功率调节能力有限。文献[12，13]通过控制机组桨距角调整机组的输出功率，但机组转速仍根据最大风能追踪模块查表控制，易使转速和桨距角之间产生不必要的重叠调整。文献[14-17]提出将风速分为高、中、低三段，针对不同分段采用不同控制策略，协调控制机组的转速和桨距角以实现降出力运行。但对如何合理确定风速分段以及不同分段之间控制策略的切换没有深入研究。文献[18]对DFIG提供功率备用的多种控制策略进行了仿真对比。另外，文献[10-18]均在所提有功控制策略的基础上提出了机组参与电网调频的方法。以上文献通过调整机组转速和桨距角均使机组能够在限电弃风工况下运行，并为电网提供频率支撑。但转速和桨距角的频繁动作易使机组产生机械疲劳，影响其使用寿命，而以上文献均未对这一问题进行考虑，难以应用于实际。

本文提出一种限电弃风工况下双馈风电机组有功及调频控制策略。基于机组运行点转移轨迹优化模型，该控制策略通过建立机组运行轨迹和调频控制器，并对变桨系统和转子侧变频器的传统控制策略进行改进，以最大程度减少机组在执行限电弃风命令和参与电网一次调频时转速和桨距角的综合调整量，延长机组的使用寿命。最后通过仿真验证所提控制策略的可行性。

1 双馈风电机组模型

双馈风电机组主要由风轮、传动轴和双馈异步电机等构成。风轮从风能中吸收的机械功率可表示为

(1)

式中：Pm为风轮吸收的机械功率；Pnom为机组的额定功率；ωr为风轮转速；Tm为机械转矩；CP为风能利用系数；λ为叶尖速比；β为叶片桨距角；ρ为空气密度；R为风轮半径；Vw为风速。

风能利用系数CP可进一步表示为

(2)

式中：c1～c8均为与风轮气动特性相关的常数；ωn为机组的额定转速。

本文中传动轴和双馈异步电机采用的模型与文献[19]中所建立的数学模型相同。

2 限电弃风工况下DFIG有功及调频控制策略

2.1 DFIG运行点的稳定性分析

正常情况下，DFIG以获得最大经济效益为目标，运行于风能最大化利用状态[19]。限电弃风运行时，需要调整DFIG的转速和桨距角，使其偏离风能最大化利用状态下的运行点，从而减少机组从风中吸收的机械功率。由式(1)和式(2)可知，机组吸收的机械功率为风速、转速和桨距角的连续非线性函数。当风速和机组应吸收的机械功率不变时，机组可以运行于不同的转速和桨距角。图1显示了风速为11 m/s时，不同功率水平下机组转速与桨距角的对应情况。

图1 不同功率水平下机组转速与桨距角的对应关系Fig.1 Relationship between rotor speed and pitch angle for different active power output

需要指出的是，图1中某些限电弃风运行点并不都能使机组在该点稳定运行，对此作如下分析。如图2所示，当风速为9 m/s、功率输出命令为0.5 MW时，存在A、B两个运行点均能使风电机组满足限电弃风要求。机组运行于A、B两个运行点时，其桨距角相同，但转速不同。当机组运行于A点时，则有

(3)

图2 运行点稳定性分析Fig.2 Stability analysis of operation points

当风电机组运行于B点时，则有

(4)

若风电机组运行于A点，一旦风速增大，机组吸收的机械功率会随之增大。由于机组吸收的机械功率大于输出功率，会导致机组转速进一步增大。由式(3)可知，机组转速的增大会迫使机组吸收更多的机械功率，使得机组转速不断升高，逐渐偏离运行点A；风速减小时风电机组运行情况与此类似，因此，风电机组并不能在A点稳定运行，也就是说，A点是一个不稳定的限电弃风运行点。若风电机组运行于B点，风速增大也会使机组转速升高。但由式(4)可知，增大的机组转速会导致机组吸收的机械功率减小，从而迫使机组回到运行点B；风速减小时风电机组的运行情况与此类似，因此风电机组能够在B点稳定运行，或说B点为稳定的限电弃风运行点。通过分析可知，式(4)成为确保机组能够在特定限电弃风运行点稳定运行的必要条件。

2.2 DFIG运行点的转移轨迹优化模型

如图3所示，t0时刻风速为11 m/s，风电机组稳定运行于A点，其输出功率为0.6 MW。t1时刻风速减小为10 m/s，而输出功率仍须保持不变，则风电机组的运行点需从A点转移至线条2上某运行点。线条2中虚线和实线分别为能使机组在t1时刻输出功率为0.6 MW的不稳定运行点和稳定运行点的集合。若机组从A点转移至B1点或B2点，转速和桨距角所需的综合调整量最小。但由于B1点不稳定，所以机组由运行点A转移至运行点B2，既能使机组的输出功率满足要求，又能使其转速和桨距角的综合调整量最小。

图3 双馈风电机组运行点转移轨迹Fig.3 The transfer trajectory of operation points for DFIG

为获得机组运行点的最优转移轨迹，首先建立以机组运行点在相邻时刻转移时转速和桨距角的综合调整量最小为目标函数、以机组有功平衡和运行点稳定性等为约束条件的非线性优化模型Ⅰ，如式(5)～式(10)所示。式(5)为优化模型的目标函数，式中两项分别表示机组转速和桨距角在相邻时刻之间的调整量。式(6)和式(7)分别为机组桨距角及转速的限值约束。式(8)确保机组能够稳定运行于选定的运行点。式(9)和式(10)为机组的有功平衡约束。

(5)

(6)

(7)

(8)

(9)

(10)

若限电弃风命令大于机组可输出的最大功率，将导致优化模型Ⅰ不存在可行解，易使机组失稳。因此，本文在每次求解优化模型Ⅰ时均对所得优化结果进行判断，如可行，则将其直接输出；否则，将功率不平衡项加入到优化模型Ⅰ的目标函数中，形成新的目标函数，如式(11)所示，将式(10)中的有功平衡约束替换为式(12)中的功率极限约束，并结合式(6)～式(9)形成新的优化模型Ⅱ并求解。

(11)

(12)

式中：Pmax、Pmin分别为机组输出功率的最大和最小值；λ为拉格朗日因子。

2.3 DFIG的有功及调频控制策略

基于机组运行点的转移轨迹优化模型，本文通过建立运行轨迹控制器和调频控制器，并对机组变桨系统和转子侧变频器的传统控制策略进行了改进，能够使DFIG在准确执行限电弃风命令以及参与电网调频的过程中，最大程度的减小其转速和桨距角的综合调整量，限电弃风工况下DFIG有功及调频控制策略如图4所示。

图4 双馈风电机组有功及调频控制策略Fig.4 Proposed control strategy of active power and frequency regulation of DFIG

2.3.1 运行轨迹控制器

本文利用Matlab调用基于内点法的Ipopt工具包[21]对优化模型Ⅰ和优化模型Ⅱ进行求解，经大量仿真实验，优化模型Ⅰ或Ⅱ求解一次仅需0.02～0.04 s。因此，本文取0.1 s作为机组运行轨迹控制器的采样周期，能够使该控制器在采样周期内完成对运行点转移轨迹优化模型的求解，以获得机组运行点的最优转移轨迹。并且，如果将运行轨迹控制器利用C语言或其他编程语言嵌入到风电机组的控制系统中，将会进一步减少优化模型的求解时间，能够满足风电机组实际运行需求。

2.3.2 变桨系统及转子侧变频器的控制策略

2.3.3 调频控制器

本文在所提有功控制策略的基础上，通过引入下垂控制建立了调频控制器，使DFIG能够模拟常规同步发电机组的调频特性，具备了参与电网一次调频的能力，如图4所示。f、fn分别为电网频率的实际值和额定值，均为标么值。RD为下垂控制系数，反映了风电机组的调频能力。

考虑到风力发电的特殊性，可参照电网对于常规同步发电机组调频能力的规定，适当放宽对风电机组调频能力的要求[16]。电网中常规同步发电机组的调差系数σg%一般为5，则风电机组的调差系数σw%为

σw%=Kf·σg%

(13)

式中Kf为风电机组相对于常规机组调差系数放宽的比例，Kf>1，Kf越大表示电网对风电机组的调频能力要求越低。于是，下垂控制系数RD为[28]

(14)

式中ΔP1为响应电网频率变化的功率增量。本文取Kf=2，根据计算结果将下垂系数RD设为10。

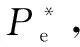
3 算例仿真

3.1 有功控制策略仿真

为验证本文所提基于机组运行点转移轨迹优化的有功功率控制策略的可行性，本文对该控制策略进行仿真，仿真结果如图5所示。

图5 有功控制策略仿真结果Fig.5 Simulation results of the active power control strategy

图5a为某风电场的实测风速，风速数据的采样周期为1 s，仿真中两个采样点之间的数据通过线性插值补充。t=20 s时，风电机组由最大风能追踪状态切换至限电弃风运行状态，执行图5d所示限电弃风命令。如图5d和图5e所示，当限电弃风命令小于机组最大可输出功率时，优化模型Ⅰ存在可行解，运行轨迹控制器通过求解优化模型Ⅰ获得机组转速、桨距角和应吸收机械功率的控制命令，使机组能够准确执行限电弃风命令；当限电弃风命令大于机组的最大可输出功率时，优化模型Ⅰ不存在可行解。为保证机组运行的稳定性，运行轨迹控制器重新求解优化模型Ⅱ以获得相应的控制命令，使机组输出最大可输出的功率。由图5b～图5d可知，风电机组的转速和输出功率均能实现对转速控制命令和功率控制命令的追踪，且追踪效果较好；而风电机组的桨距角也在运行过程中逐渐向桨距角控制命令逼近，实现了对桨距角控制命令的追踪。由图5f可知，双馈风电机组在运行过程中，变频器直流环节的电容电压一直保持稳定。因此，利用本文所提有功功率控制策略，能使风电机组在准确执行调度部门限电弃风命令过程中，沿运行点的最优转移轨迹运行。

为评价风电机组在执行限电弃风命令过程中转速和桨距角的动作程度，本文定义了转速调整量Δωr、桨距角调整量Δβ和综合调整量Δz三种评价指标为

(15)

采用相同的仿真条件，本文对文献[13，15]中所提有功控制策略分别进行仿真，并将仿真结果与本文所提控制策略进行对比，对比结果表明本文所提有功控制策略能够大大减小机组在限电弃风运行过程中转速和桨距角的调整量，如表1所示。

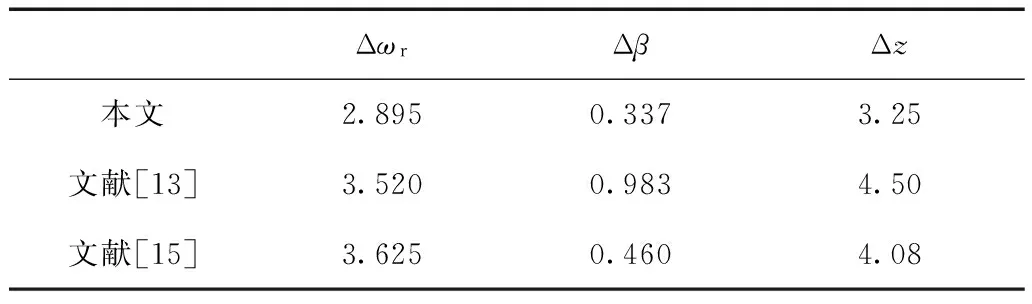
表1 不同控制策略下转速和桨距角调整量对比Tab.1 Comparation of rotor speed and pitch angle adjustment for different control strategies

3.2 调频控制策略仿真

为验证本文所提机组调频控制策略的可行性，对图6所示系统进行仿真：水电机组G1的容量为200 MV·A，通过10.5/110 kV变压器T1接入电网，然后经40 km输电线路连接于110/35 kV变压器T2的高压侧，变压器T2的低压侧与35 kV负载母线相连。风电场由40台额定容量为1.55 MV·A的双馈风电机组构成，经0.69/35 kV变压器T3接入电网，然后通过10 km输电线路连接于35 kV负载母线。系统中有L1和L2两个负载，负载L1为恒定负载，负载L2通过断路器控制。风速保持15 m/s不变，风电场运行于限电弃风状态，限电弃风命令为0.8 pu，并保持不变。t=70 s时，负载L2瞬间投入，仿真结果如图7所示。

图6 仿真系统图Fig.6 Diagram of the simulation system

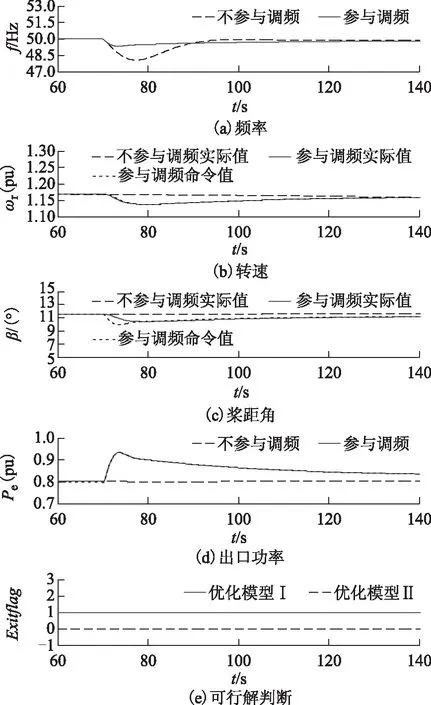
图7 调频控制策略仿真结果Fig.7 Simulation results of the frequency regulation control strategy

由图7所示仿真结果可知，当风电机组控制系统中未配置调频控制器时，双馈风电机组不具有自动响应电网频率变化的能力。而当风电机组控制系统中配置了调频控制器后，双馈风电机组能够在限电弃风运行工况下沿机组运行点的最优转移轨迹响应电网的频率变化，参与电网一次调频，大大减少了其频率的跌落程度，提高了系统的稳定性。

4 结论

本文针对双馈风电机组，提出一种基于机组运行点转移轨迹优化的有功及调频控制策略。仿真结果表明：本文所提有功控制策略适用于限电弃风工况下双馈风电机组的运行控制；利用本文所提有功控制策略，能够减轻机组在限电弃风运行过程中产生的机械疲劳，有助于延长机组使用寿命；通过引入下垂控制，使双馈风电机组在所提有功控制策略的基础上具备了参与电网一次调频的能力。

附 录

附表1 双馈风电机组主要参数
App.Tab.1 The major parameters of DFIG

参数数值参数数值R/m35c521c10.6450c60.00912c2116c70.08c30.4c80.035c45

[1] GWEC.Global installed wind power capacity(MW)-regional distribution[R].2014.

[2] GB/T 19963—2011，风电场接入电力系统技术规定[S].北京：中国标准出版社，2011.

[3] EON Netz GmbH.Grid code-high and extra high voltage[EB/OL].[2006-06-02].http：//www.nerc.com/docs/pc/ivgtf/German _EON_Grid_Code.pdf.

[4] Nordel.Nordic grid code 2007 (Nordic collection of rules)[EB/OL].2004.http：//webhotel2.tut.fi/units/set/research/adine/materiaalit/Active%20network/ System%20integration/Grid%20codes/Nordel%20grid% 20code%202007-00129-01-E.pdf.

[5] 梅华威，米增强，白俊良.风电场及机组出力损失计算模型与方法[J].电力系统自动化，2014，38(2)：12-16. Mei Huawei，Mi Zengqiang，Bai Junliang.Calculation model and method of output power loss of wind farms and wind turbines[J].Automation of Electric Power Systems，2014，38(2)：12-16.

[6] 王乾坤.国内外风电弃风现状及经验分析[J].华东电力，2012，40(3)：378-381. Wang Qiankun.Update and empirical analysis of domestic and foreign wind energy curtailment[J].East China Electric Power，2012，40(3)：378-381.

[7] 刘巨，姚伟，文劲宇，等.大规模风电参与系统频率调整的技术展望[J].电网技术，2014，38(3)：638-646. Liu Ju，Yao Wei，Wen Jinyu，et al.Prospect of technology for large-Scale wind farm participating into power grid frequency regulation[J].Power System Technology，2014，38(3)：638-646.

[8] 刘新东，方科，陈焕远，等.利用合理弃风提高大规模风电消纳能力的理论研究[J].电力系统保护与控制，2012，40(6)：35-39. Liu Xindong，Fang Ke，Chen Huanyuan，et al.Research on rational wind power casting theory for large-scale wind power integration improvement[J].Power System Protection and Control，2012，40(6)：35-39.

[9] 邹见效，李丹，郑刚，等.基于机组状态分类的风电场有功功率控制策略[J].电力系统自动化，2011，35(24)：28-32. Zou Jianxiao，Li Dan，Zheng Gang，et al.An active power control scheme for wind farms based on state classification algorithm[J].Automation of Electric Power Systems，2011，35(24)：28-32.

[10]De Almeida R G，Castronuovo E D，Peas Lopes J A.Optimum generation control in wind parks when carrying out system operator requests[J].IEEE Transactions on Power Systems，2006，21(2)：718-725.

[11]De Almeida R G，Peas Lopes J A.Participation of doubly fed induction wind generators in system frequency regulation[J].IEEE Transactions on Power Systems，2007，22(3)：944-950.

[12]Holdsworth L，Ekanayake J B，Jenkins N.Power system frequency response from fixed speed and doubly fed induction generator-based wind turbines[J].Wind Energy，2004，7(1)：21-35.

[13]Moutis P，Loukarakis E，Papathanasiou S，et al.Primary load-frequency control from pitch-controlled wind turbines[C].IEEE Bucharest Power Tech Conference，Bucharest，2009：1-7.

[14]张昭遂，孙元章，李国杰，等.超速与变桨协调的双馈风电机组频率控制[J].电力系统自动化，2011，35(17)：20-25，43. Zhang Zhaosui，Sun Yuanzhang，Li Guojie，et al.Frequency regulation by doubly fed induction generator wind turbines based on coordinated overspeed control and pitch control[J].Automation of Electric Power Systems，2011，35(17)：20-25，43.

[15]Le Ren Chang Chien，Yao Ching Yin.Strategies for operationg wind power in a similar manner of conventional power plant[J].IEEE Transactions on Power Systems，2009，24(4)：926-934.

[16]吴子双，于继来，彭喜云.高风速段次优功率追踪方式的风电调频方法[J].电工技术学报，2013，28(5)：112-119. Wu Zishuang，Yu Jilai，Peng Xiyun.DFIG’s frequency regulation method only for high wind speed with suboptimal power tracking[J].Transactions of China Electro Technical Society，2013，28(5)：112-119.

[17]Andraz Zertek，Gregor Verbic，Milos Pantos.A novel strategy for variable-speed wind turbines’ participation in primary frequency control[J].IEEE Transactions on Energy Convention，2012，3(4)：791-799.

[18]Jeong Y，Johnson K，Fleming P.Comparison and testing of power reserve control strategies for grid-connected wind turbines[J].Wind Energy，2014，17(3)：343-358.

[19]贺益康，胡家兵，徐烈.并网双馈异步风力发电机运行控制[M].北京：中国电力出版社，2012.

[20]Forsgren A，Gill P E，Wright M H.Interior methods for nonlinear optimization[J].SIAM Review，2002，44(4)：525-597.

[21]Wächter A，Biegler L T.On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming[J].Mathematical Programming，2006，106(1)：25-57.

[22]Ulbrich M，Ulbrich S，Vicente L N.A globally convergent primal-dual interior-point filter method for nonlinear programming[J].Mathematical Programming，2004，100(2)：379-410.

[23]Wächter A，Biegler L T.Line search filter methods for nonlinear programming：motivation and global convergence[J].SAIM Journal on Optimization，2005，16(1)：1-31.

[24]刘明波，王晓村.内点法在求解电力系统优化问题中的应用综述[J].电网技术，1999，21(8)：61-64. Liu Mingbo，Wang Xiaocun.An applications of interior point method to solution of optimization problems in power systems[J].Power System Technology，1999，21(8)：61-64.

[25]Jabr R A，Coonick A H，Cory B J.A primal-dual interior point method for optimal power flow dispatching[J].IEEE Transactions on Power Systems，2002，17(3)：654-662.

[26]郑文杰，刘明波.应用线搜索滤波器内点法求解最优协调电压控制问题[J].电工技术学报，2012，27(9)：70-77. Zheng Wenjie，Liu Mingbo.Solution of optimal coordinated voltage control using line search filter interior point method[J].Power System Technology，2012，27(9)：70-77.

[27]陶向红，卜广全，王虹富，等.基于加权最小绝对值的大电力系统潮流可行解优化恢复方法[J].电力系统自动化，2014，38(23)：60-64，76. Tao Xianghong，Bu Guangquan，Wang Hongfu，et al.An optimization method based on weighted least absolute value to restore power flow solvability of bulk power system[J].Automation of Electric Power Systems，2014，38(23)：60-64，76.

[28]陈珩.电力系统稳态分析[M].3版.北京：中国电力出版社，2007.

The Control Strategy of Active Power and Frequency Regulation of DFIG Under Wind Abandon Condition

MiZengqiang1LiuLiqing1YuYang1DuPing2YuanHe1

(1.State Key Laboratory of Alternate Electrical Power System With Renewable Energy Sources North China Electric Power University Baoding 071003 China 2.Power Dispatching Control Center State Grid East Inner Mongolia Electric Power Company Limited Hohhot 010020 China)

Doubly fed induction generator (DFIG) wind turbines can provide power reserve and frequency support for the grid under wind abandon condition.In order to reduce the mechanical fatigue caused by frequent adjustment of rotor speed and pith angle，an active power and primary frequency control strategy based on the optimization of transfer trajectory at operation points is proposed.The introduction of the droop control enables the participation of the grid frequency regulation.Firstly，the stability of the wind turbine at different operation points under wind abandon condition is analyzed.Secondly，a transfer trajectory optimization model for operation points is established.The minimum adjustment of rotor speed and pith angle is treated as the objective function；and the power balance，operation point stability et al.are considered as the constraints.A method dealing with infeasible solution is proposed to obtain the optimal feasible transfer trajectory.Finally，to realize the active power control and the grid frequency regulation，an operation trajectory and a frequency regulation controller are established and the traditional control strategies for pitch system and rotor side converter are improved，which ensures that the wind turbines can track the optimal transfer trajectory.The simulation results show that the control strategy can reduce the adjustment of rotor speed and pith angle dramatically while completing the task of wind abandon and providing frequency support for grid.

DFIG，wind abandon，primary frequency regulation，adjustment，transfer trajectory optimization

中央高校基本科研业务费专项资金(13XS20)和国家电网公司科技项目(SGMD0000DDJS1500096)资助。

2015-01-04 改稿日期2015-03-18

TM614

米增强 男，1960年生，教授，博士生导师，研究方向为新能源电力系统、电力信息处理与建模。

刘力卿 男，1987年生，博士研究生，研究方向为储能控制技术、风力发电控制技术。(通信作者)